Similar presentations:
Единичная окружность
1.
УЕдиничная
окружность
h
1
М ( х; у )
α
О
1
Х
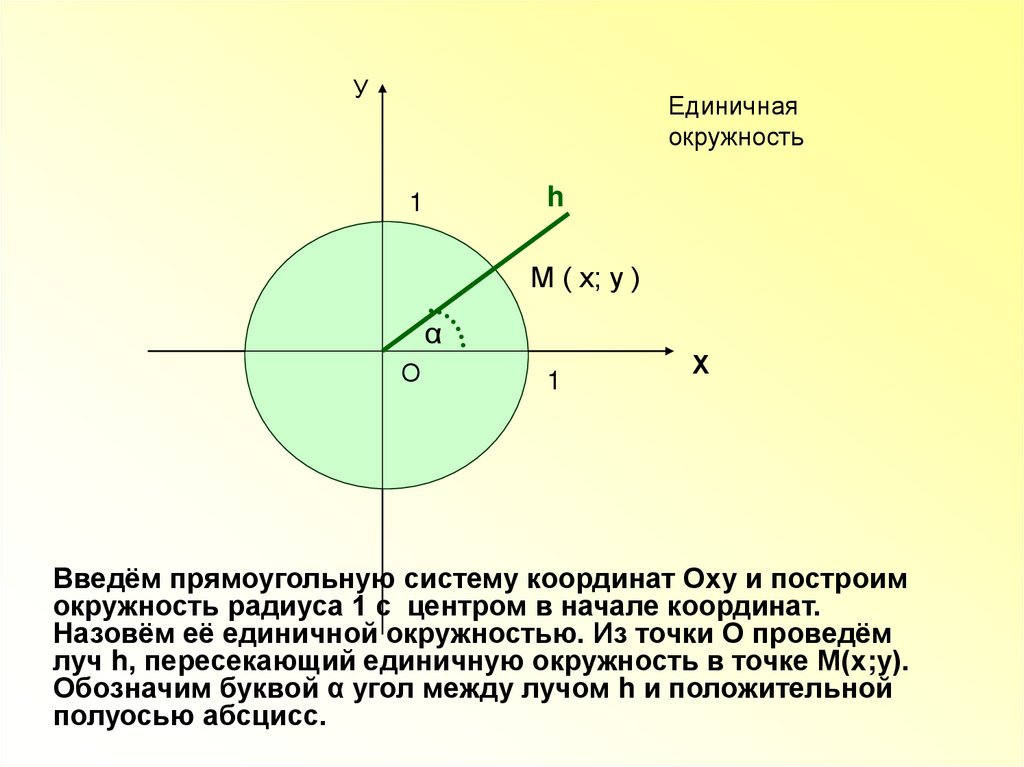
Введём прямоугольную систему координат Оху и построим
окружность радиуса 1 с центром в начале координат.
Назовём её единичной окружностью. Из точки О проведём
луч h, пересекающий единичную окружность в точке М(х;у).
Обозначим буквой α угол между лучом h и положительной
полуосью абсцисс.
2.
Если угол α острый, то изпрямоугольного ∆DOM имеем
У
МД
ОД
sin α =
, cos α =
ОМ
ОМ
h
1
Но OM = 1, MD = у, OD = х,
поэтому
М ( х; у )
α
О Х
sin α = у, cos α = х.
У
Д
1
.
Х
Таким образом, для любого угла
из промежутка
0°≤ α ≤180°
синусом угла α называется
ордината у точки М,
а косинусом угла α – абсцисса х
точки М
Так как координаты (х; у) точек единичной полуокружности
заключены в промежутках 0 у 1, -1 х 1, то для любого α
из промежутка 0°≤ α ≤180° справедливо неравенство
0 sin α 1,
-1 cos α 1.
3.
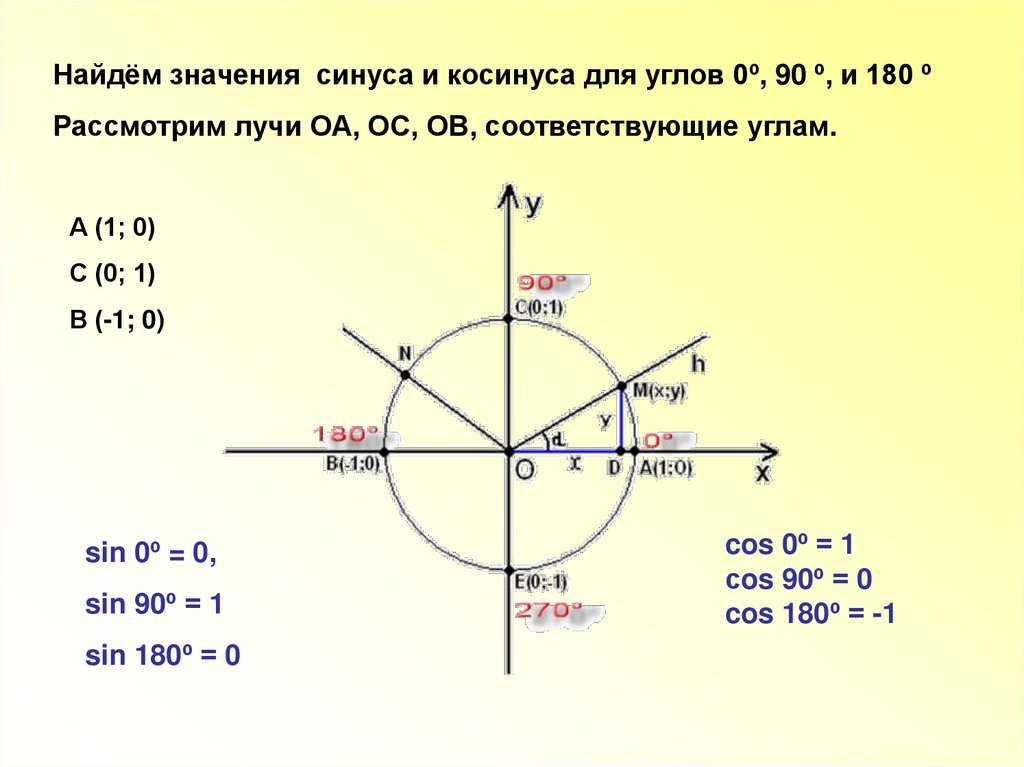
Найдём значения синуса и косинуса для углов 0º, 90 º, и 180 ºРассмотрим лучи ОА, ОС, ОВ, соответствующие углам.
А (1; 0)
С (0; 1)
В (-1; 0)
sin 0º = 0,
sin 90º = 1
sin 180º = 0
cos 0º = 1
сos 90º = 0
cos 180º = -1
4.
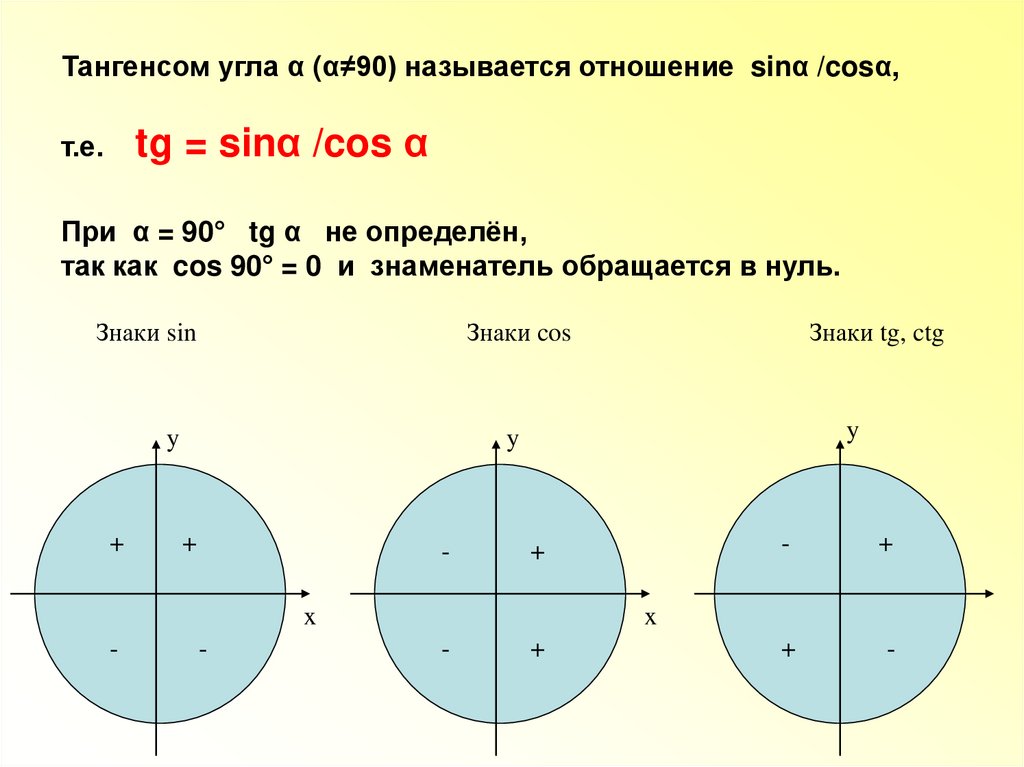
Тангенсом угла α (α≠90) называется отношение sinα /cosα,tg = sinα /cos α
т.е.
При α = 90° tg α не определён,
так как cos 90° = 0 и знаменатель обращается в нуль.
Знаки sin
Знаки cos
y
+
y
y
+
-
+
x
-
Знаки tg, ctg
-
-
+
+
-
x
-
+
5.
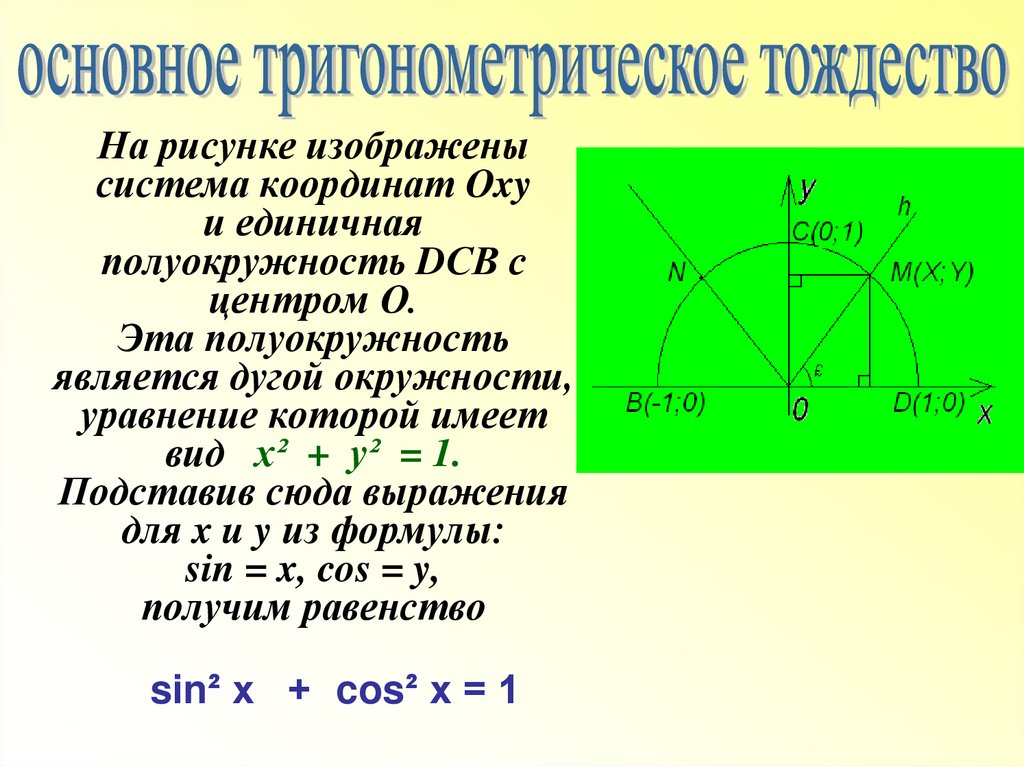
На рисунке изображенысистема координат Оxy
и единичная
полуокружность DСВ с
центром О.
Эта полуокружность
является дугой окружности,
уравнение которой имеет
вид х² + у² = 1.
Подставив сюда выражения
для x u y из формулы:
sin = x, cos = y,
получим равенство
sin² х + cos² х = 1
6.
sin (90º - α) = cos αcos (90º - α) = sin α
sin (180º - α) = sin α
cos (180º - α) = - cos α
при
0° ≤ α ≤ 180°
7.
Составьте таблицу значенийсинуса, косинуса и тангенса для
углов 0º, 30 º, 45 º, 60 º, 90 º,
120 º, 135 º, 150 º, 180 º.
8.
3sin120º = sin (180º - 60º) = sin 60º =
2
1
3
1
3
tg 150º = sin150º : cos 150º =
: ()==3
3
2
2
Заполните таблицу
α
α
30°
Sin α 30°
45°
60°
90°
180°
270°
360°
45° 60° 90° 180° 270° 360°
SinCos
α α 1/2 √2/2 √3/2
Costgαα √3/2 √2/2 1/2
√3
Tg α √3/3 1
1
0
Не
определён
0
-1
0
-1
0
Не
определён
0
1
0
0°
0°
0
1
0





 mathematics
mathematics








