Similar presentations:
Тригонометрия. Углы
1.
2.
Выразите угол в радианахс помощью :
7
3
3
5
2
150°=
360°=
- -720°=
210°=
270°=
180°=
45°=
90°=
60°=
135°=
30°= 24
46
6364
2
3.
Найдите градусную меруугла, радианная мера
которого равна:
53 2
540°
300°
72°
18°
33 10
108°
55
4.
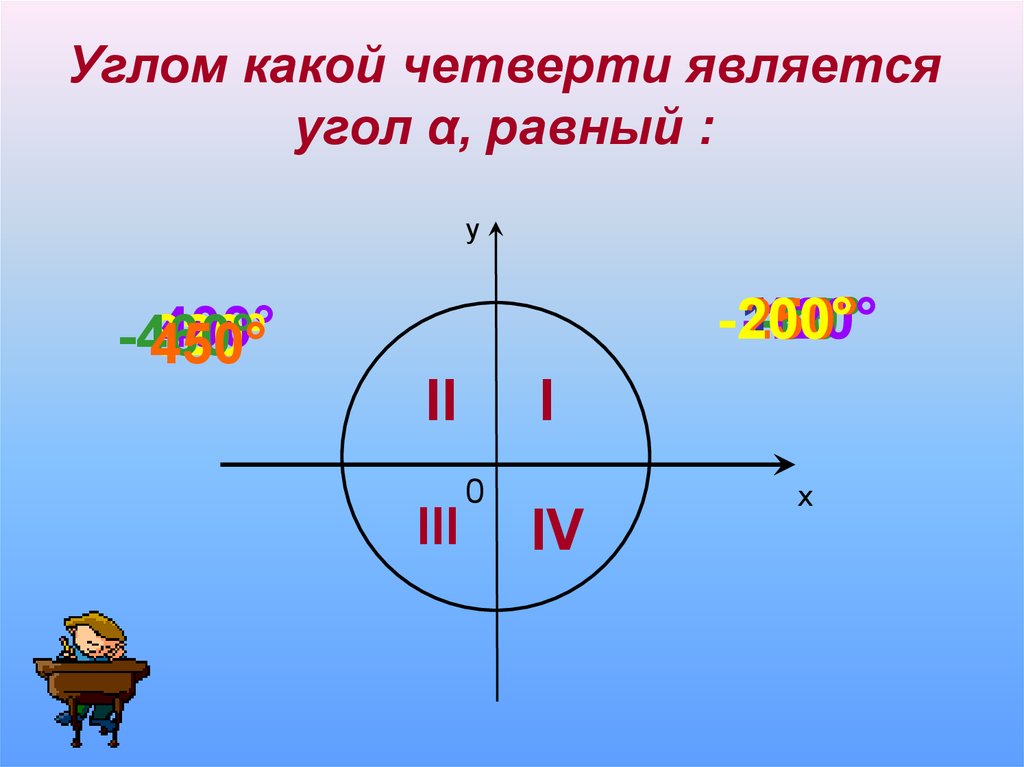
Углом какой четверти являетсяугол α, равный :
у
-200°
250°
-120°
150°
-80°
45°
400°
-460°
820°
450°
II
III
I
0
IV
х
5. Синус , косинус, тангенс и котангенс угла из промежутка [0°; 180°]
СИНУС , КОСИНУС, ТАНГЕНС И КОТАНГЕНСУГЛА ИЗ ПРОМЕЖУТКА [0°; 180°]
6. Продолжите фразу:
АС
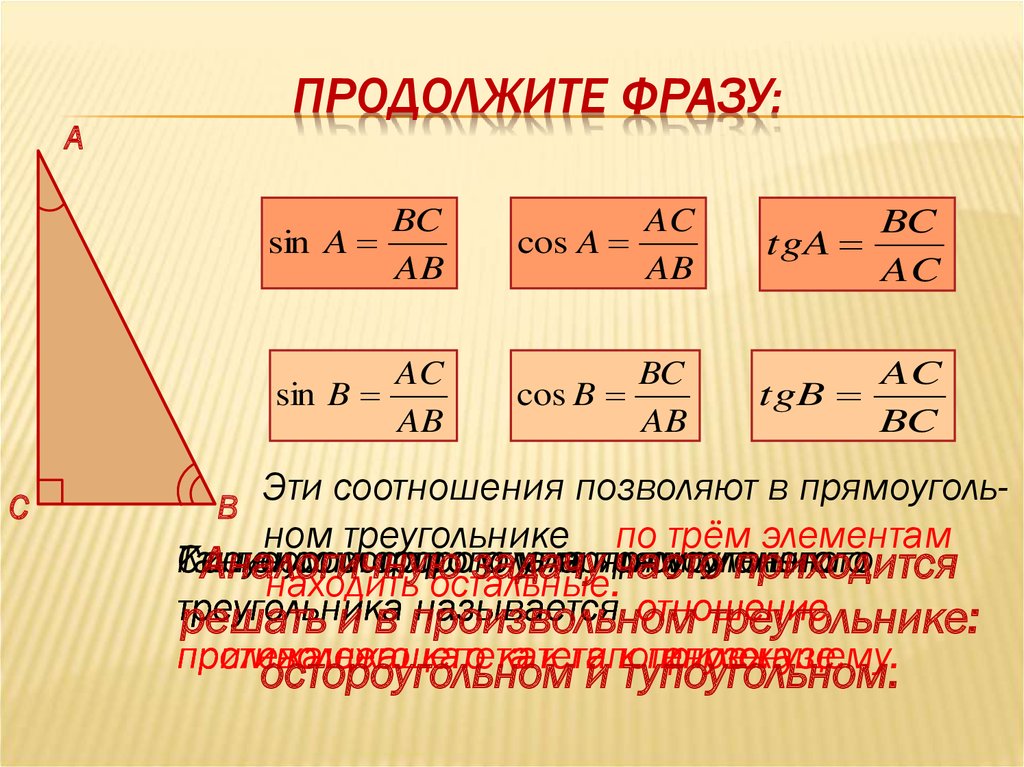
ПРОДОЛЖИТЕ ФРАЗУ:
BC
sin A
AB
AC
cos A
AB
BC
tgA
AC
AC
sin B
AB
BC
cos B
AB
AC
tgB
BC
Эти
соотношения
позволяют
в
прямоугольВ
ном треугольнике по трём элементам
Синусом
Косинусом
Тангенсом
острого
острого
острого
угла
угла
угла
прямоугольного
прямоугольного
прямоугольного
Аналогичную
задачу
находить остальные.часто приходится
треугольника
называется отношение
решать и в произвольном
треугольнике:
прилежащего
противолежащего
катета
катета
к гипотенузе.
гипотенузе.
прилежащему.
остороугольном
и ктупоугольном.
7. Необходимо понять!!!
НЕОБХОДИМО ПОНЯТЬ!!!1. Если существуют соотношения между сторонами и
углами в произвольном треугольнике, то что следует
считать синусом, косинусом, тангенсом острого или
тупого угла произвольного треугольника?
2. Если существуют соотношения между сторонами и
углами в произвольном треугольнике, то каковы эти
соотношения?
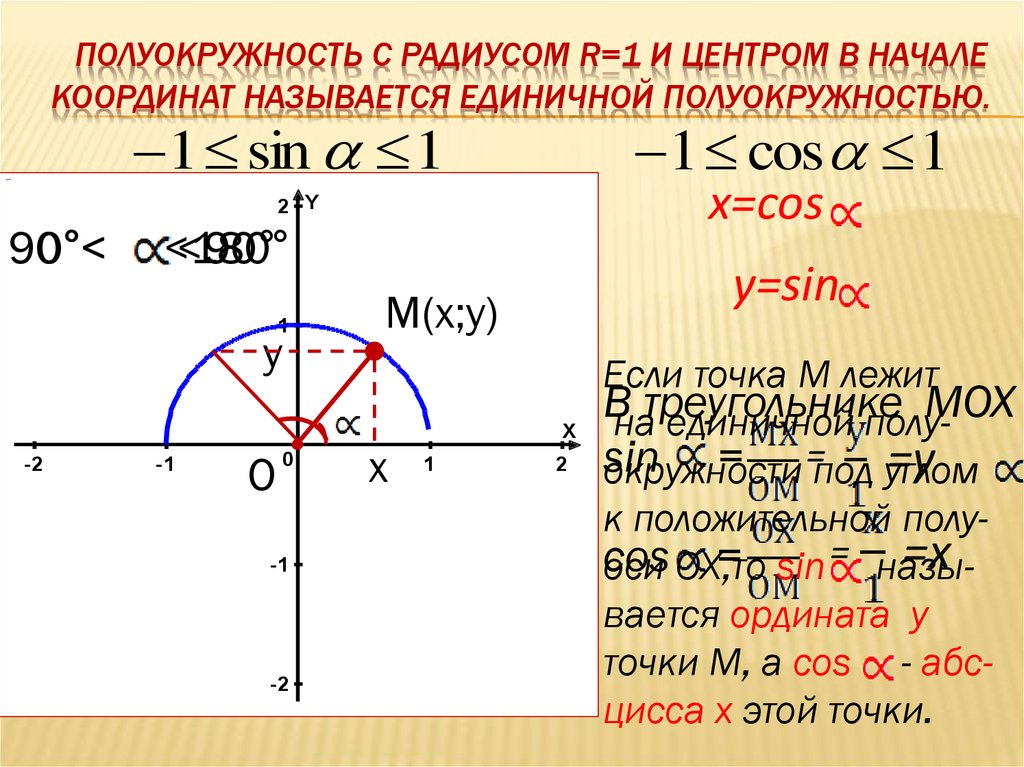
8. ПОЛУОКРУЖНОСТЬ С РАДИУСОМ R=1 И ЦЕНТРОМ В НАЧАЛЕ КООРДИНАТ НАЗЫВАЕТСЯ ЕДИНИЧНОЙ ПОЛУОКРУЖНОСТЬЮ.
1 sin 11 cos 1
x=cos
2 Y
90°<
0°<
<180°
<90°
1
у
-2
-1
О
0
-1
-2
y=sin
М(х;у)
х
X
1
2
Если точка М лежит
Внатреугольнике
МОХ
единичной полуsin
= =под углом
=у
окружности
к положительной полу=х
cos
= sin = назыоси ОХ,то
вается ордината у
точки М, а сos - абсцисса х этой точки.
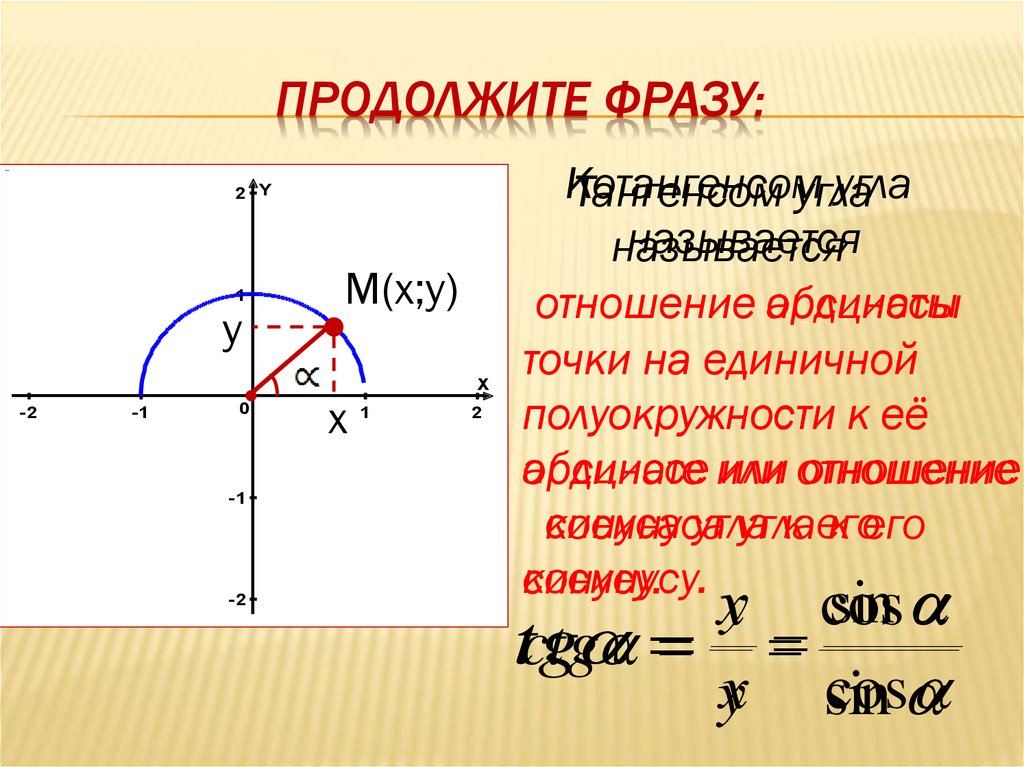
9. Продолжите фразу:
ПРОДОЛЖИТЕ ФРАЗУ:2 Y
1
у
-2
-1
0
-1
-2
М(х;у)
х
X
1
2
Котангенсом
угла
Тангенсом угла
называется
называется
отношение абсциссы
ординаты
точки на единичной
полуокружности к её
абсциссе
ординате или отношение
синуса угла
к его
косинуса
угла
к его
косинусу.
синусу.
sin
xy cos
tg
ctg
cos
yx sin
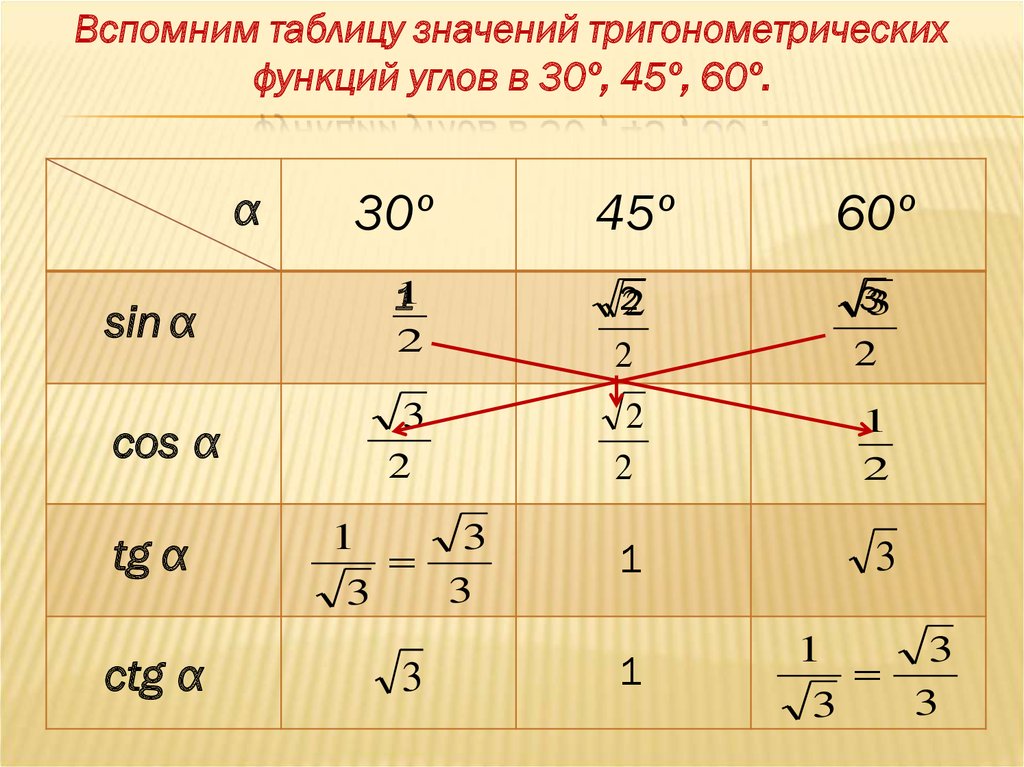
10.
Вспомним таблицу значений тригонометрическихфункций углов в 30º, 45º, 60º.
α
30º
45º
60º
sin α
1
1
2
22
2
33
3
2
2
cos α
3
2
2
2
1
2
1
3
3
3
1
3
1
1
3
3
3
tg α
ctg α
3
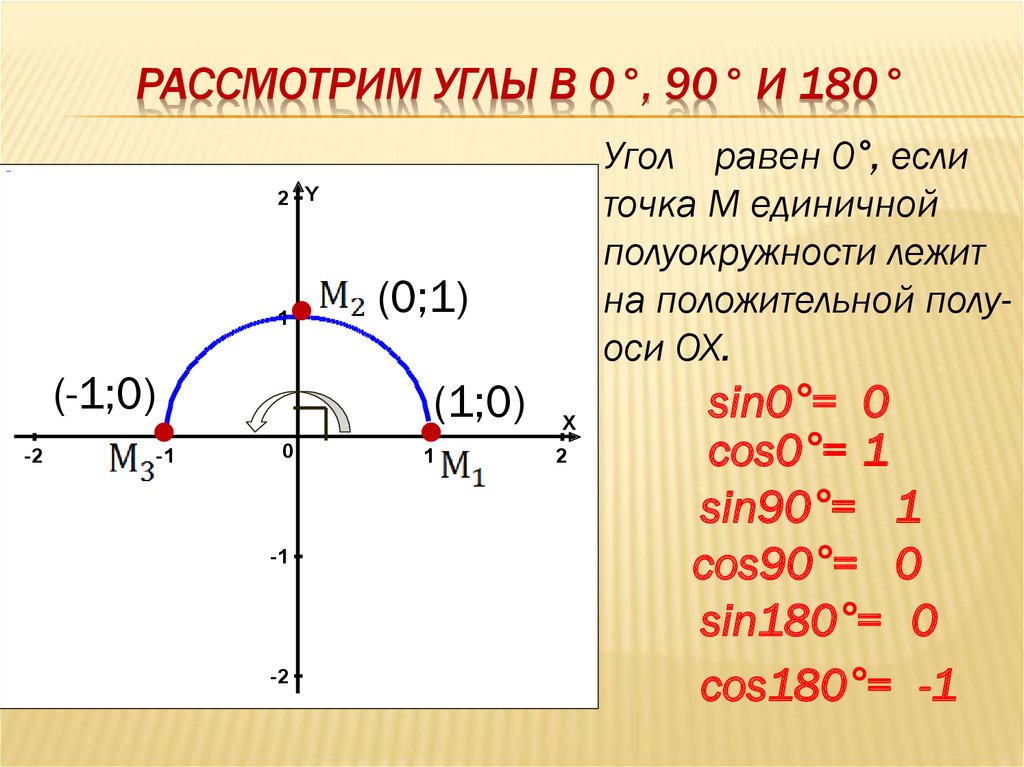
11. Рассмотрим Углы в 0°, 90° и 180°
РАССМОТРИМ УГЛЫ В 0°, 90° И 180°Угол равен 0°, если
точка М единичной
полуокружности лежит
на положительной полуоси ОХ.
2 Y
1
(-1;0)
-2
-1
(0;1)
(1;0)
0
-1
-2
1
X
2
sin0°= 0
cos0°= 1
sin90°= 1
cos90°= 0
sin180°= 0
cos180°= -1
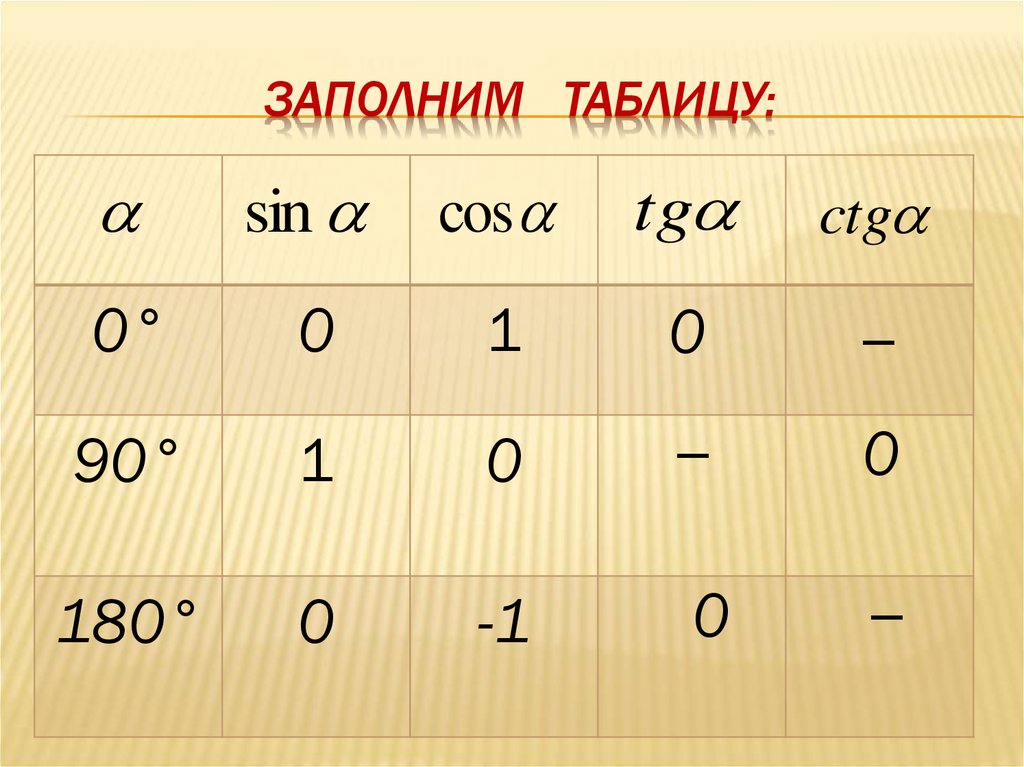
12. Заполним таблицу:
ЗАПОЛНИМ ТАБЛИЦУ:sin
cos
tg
ctg
0°
0
1
0
_
0
_
0
0
_
90°
180°
1
0
-1
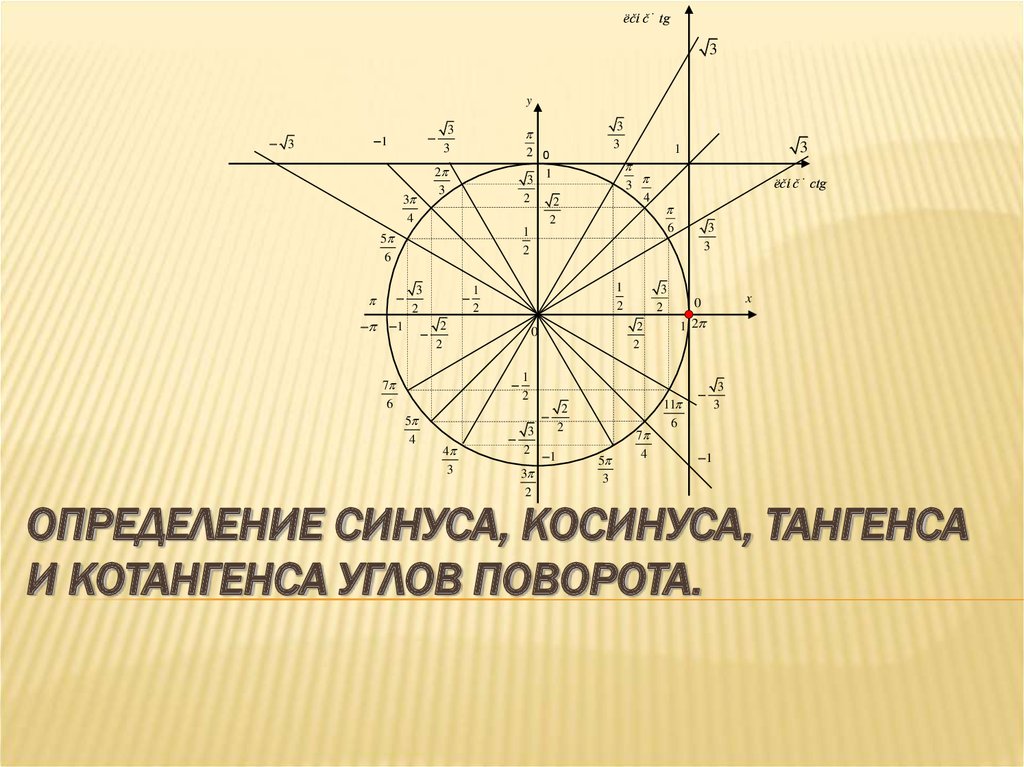
13. Определение синуса, косинуса, тангенса и котангенса углов поворота.
ëčí č˙ tg3
y
3
1
2
3
3
4
3
3
2 0
3
3
3
2
3
4
1
2
2
1
2
5
6
1
3
2
1
2
1
2
2
2
7
6
5
4
1
2
4
3
3
2
3
2
1
2
2
5
3
ëčí č˙ ctg
6
3
2
2
2
0
3
1
7
4
3
3
x
0
1 2
11
6
3
3
1
ОПРЕДЕЛЕНИЕ СИНУСА, КОСИНУСА, ТАНГЕНСА
И КОТАНГЕНСА УГЛОВ ПОВОРОТА.
14.
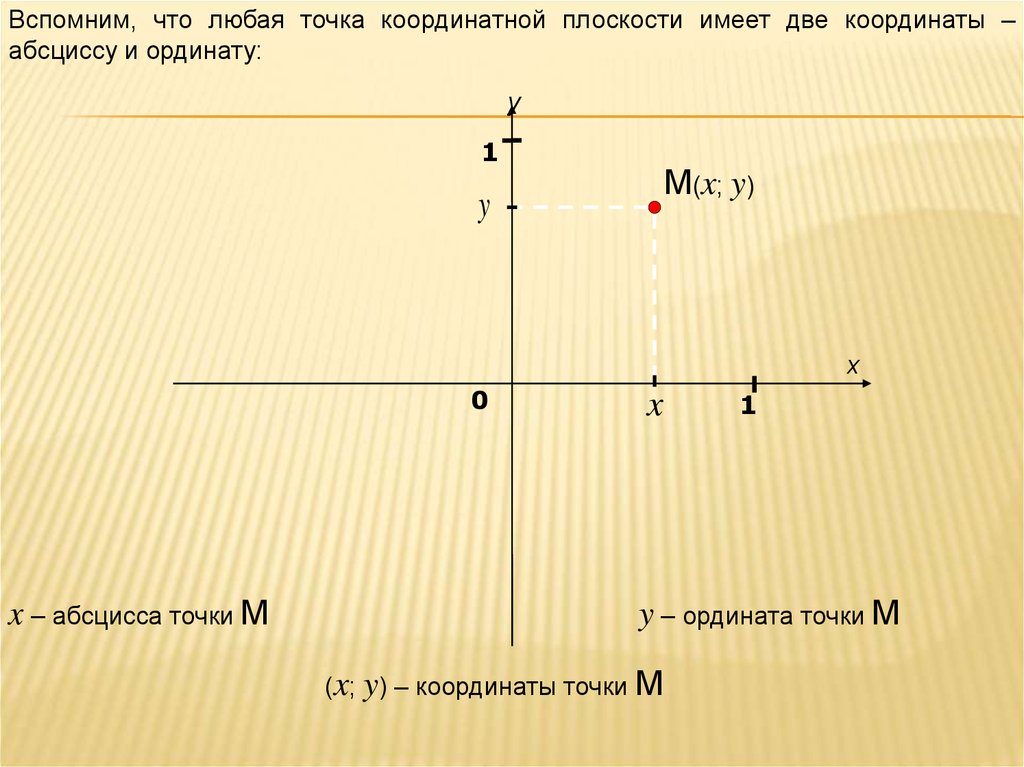
Вспомним, что любая точка координатной плоскости имеет две координаты –абсциссу и ординату:
y
1
M(x; y)
y
x
0
x – абсцисса точки M
x
1
y – ордината точки M
(x; y) – координаты точки M
15.
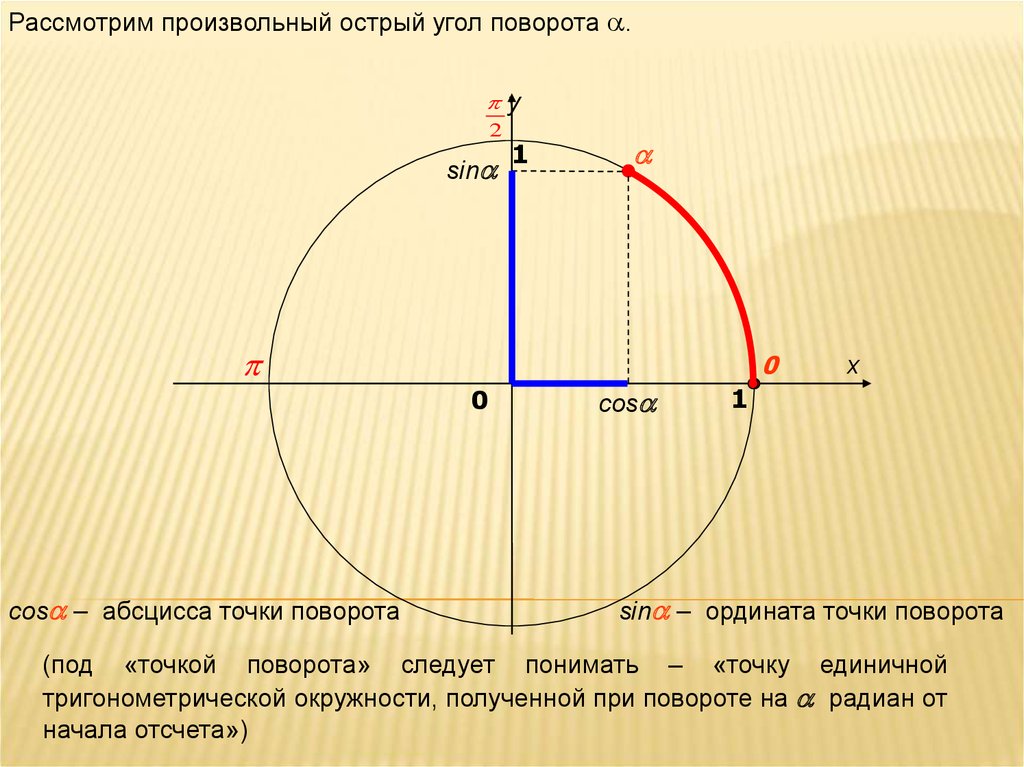
Рассмотрим произвольный острый угол поворота .2
sin
1
0
0
cos – абсцисса точки поворота
y
cos
x
1
sin – ордината точки поворота
(под «точкой поворота» следует понимать – «точку единичной
тригонометрической окружности, полученной при повороте на радиан от
начала отсчета»)
16.
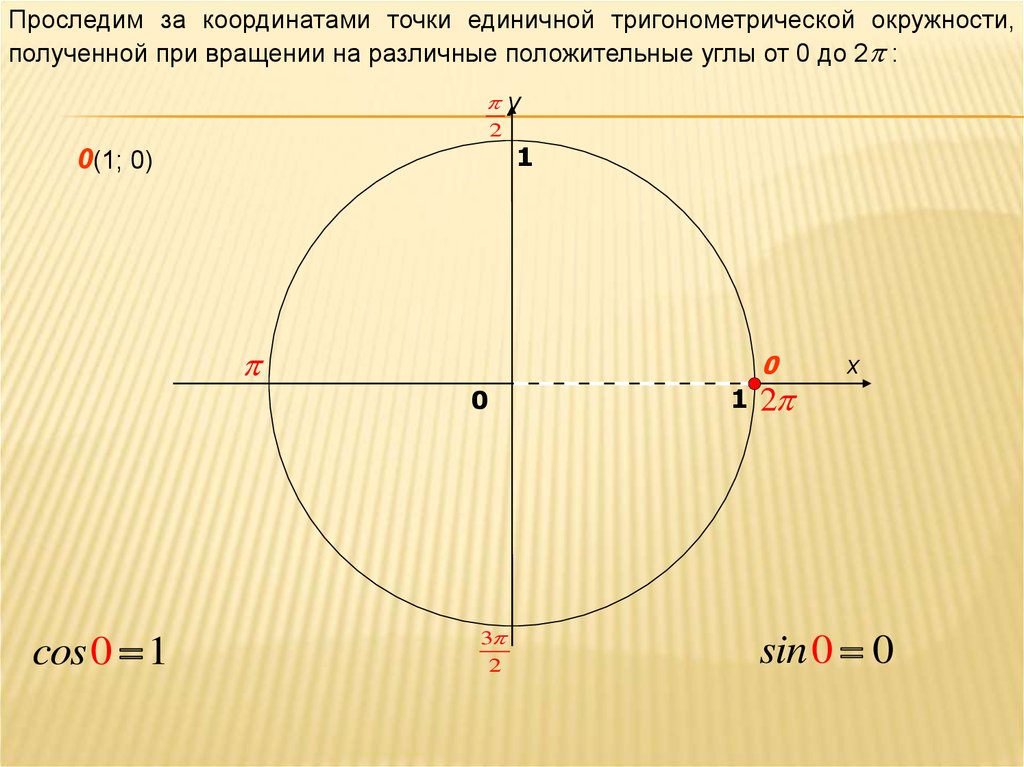
Проследим за координатами точки единичной тригонометрической окружности,полученной при вращении на различные положительные углы от 0 до 2 :
2
0(1; 0)
1
0
0
cos 0 1
y
3
2
1
2
x
sin 0 0
17.
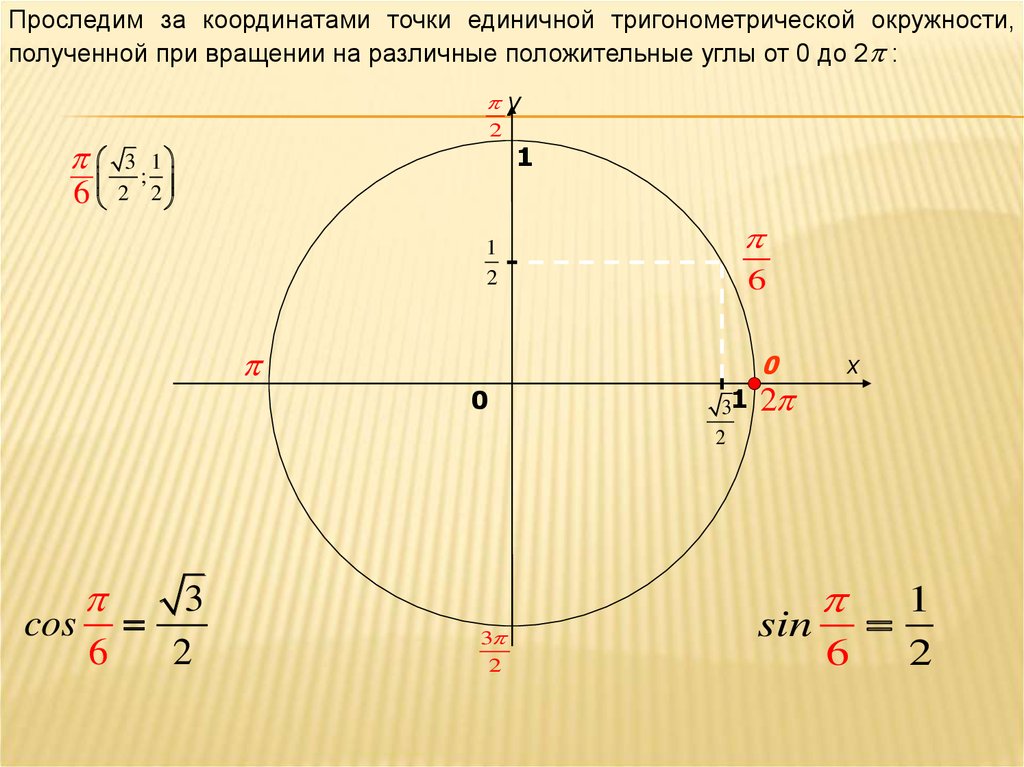
Проследим за координатами точки единичной тригонометрической окружности,полученной при вращении на различные положительные углы от 0 до 2 :
2
3 1
;
6 2 2
1
2
1
6
0
0
31
2
x
2
3
cos
6
2
y
3
2
1
sin
6
2
18.
Проследим за координатами точки единичной тригонометрической окружности,полученной при вращении на различные положительные углы от 0 до 2 :
2
2 2
;
2
2
4
y
1
2
2
1
2
4
6
0
0
2
cos
4
2
3
2
2
2
31
2
x
2
2
sin
4
2
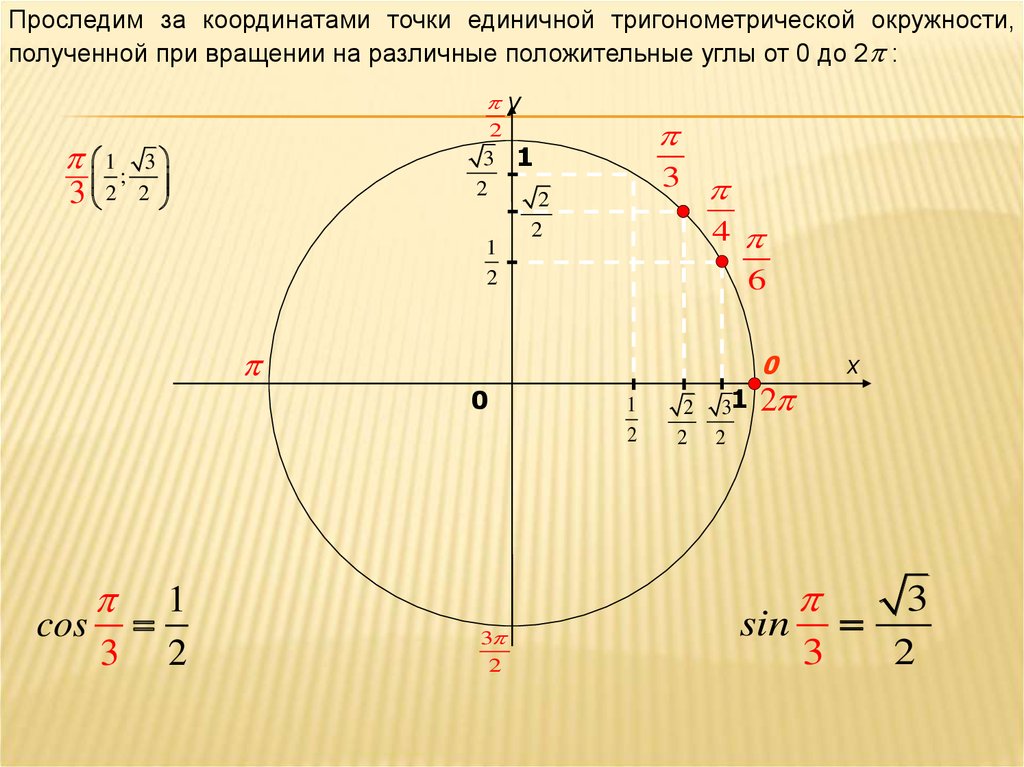
19.
Проследим за координатами точки единичной тригонометрической окружности,полученной при вращении на различные положительные углы от 0 до 2 :
2
1 ;
3
3 2 2
3
2
1
2
y
1
3
4
6
2
2
0
0
2
2
31
2
2
1
cos
3 2
1
2
x
3
2
3
sin
3
2
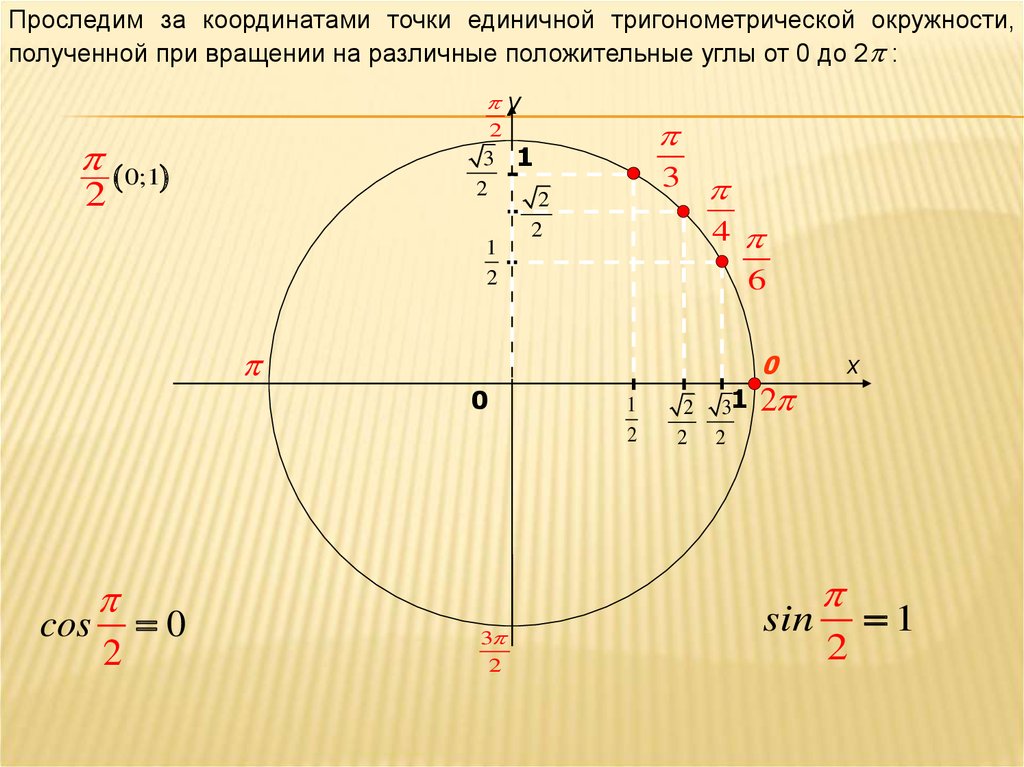
20.
Проследим за координатами точки единичной тригонометрической окружности,полученной при вращении на различные положительные углы от 0 до 2 :
2
0;1
3
2
2
1
2
y
1
3
4
6
2
2
0
0
cos
2
0
3
2
1
2
2
2
31
2
x
2
sin
2
1
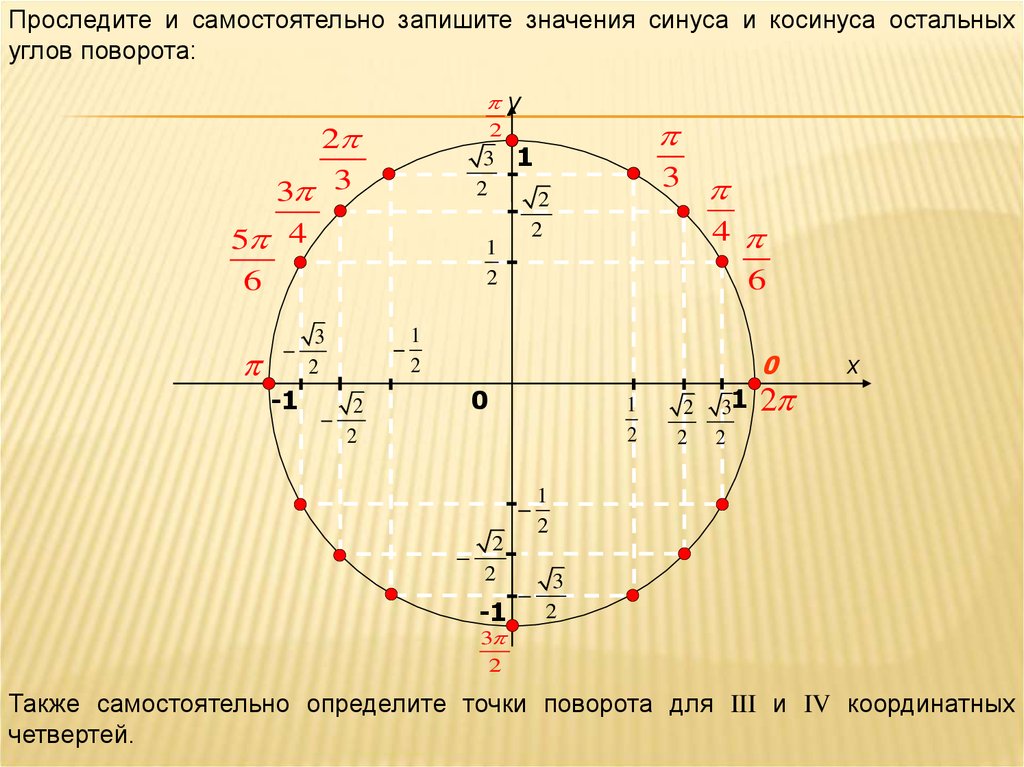
21.
Проследите и самостоятельно запишите значения синуса и косинуса остальныхуглов поворота:
2
3 3
5 4
6
-1
3
2
2
3
2
y
1
3
4
6
2
2
1
2
1
2
0
0
2
2
1
2
2
2
-1
3
2
2
2
31
2
2
x
1
2
3
2
Также самостоятельно определите точки поворота для III и IV координатных
четвертей.
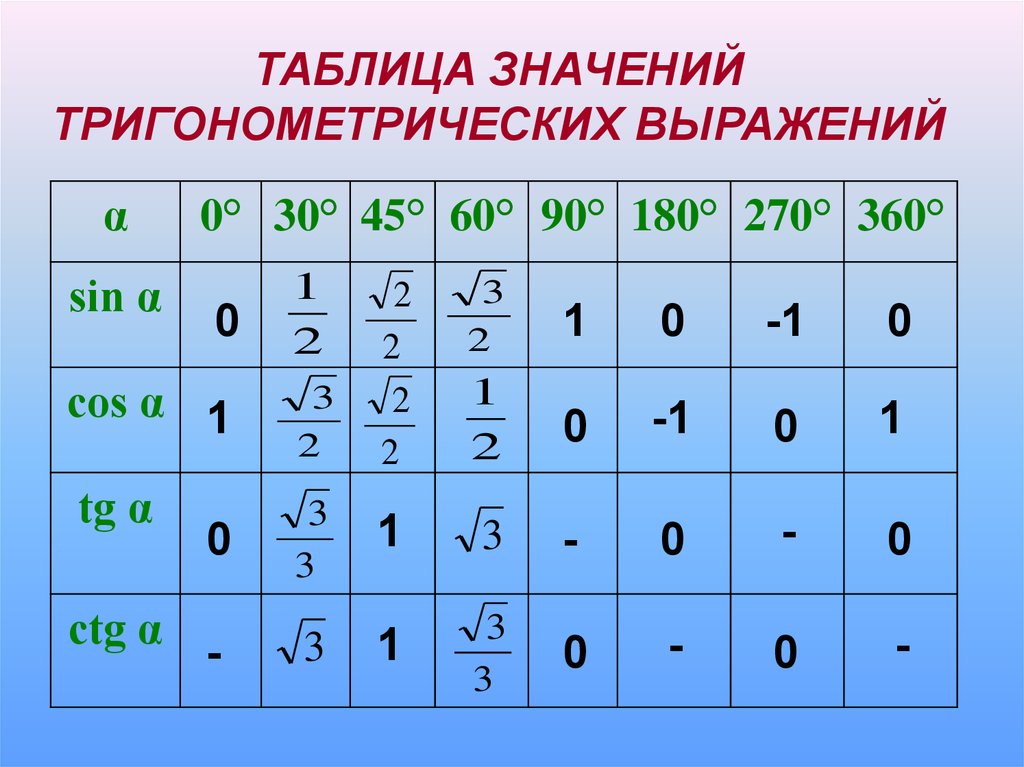
22.
ТАБЛИЦА ЗНАЧЕНИЙТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
α
sin α
0° 30° 45° 60° 90° 180° 270° 360°
0
cos α 1
tg α
ctg α
0
-
1
2
2
2
2
2
3
2
1
0
-1
0
1
2
0
-1
0
1
3
3
1
3
-
0
-
0
3
1
3
3
0
-
0
-
3
2
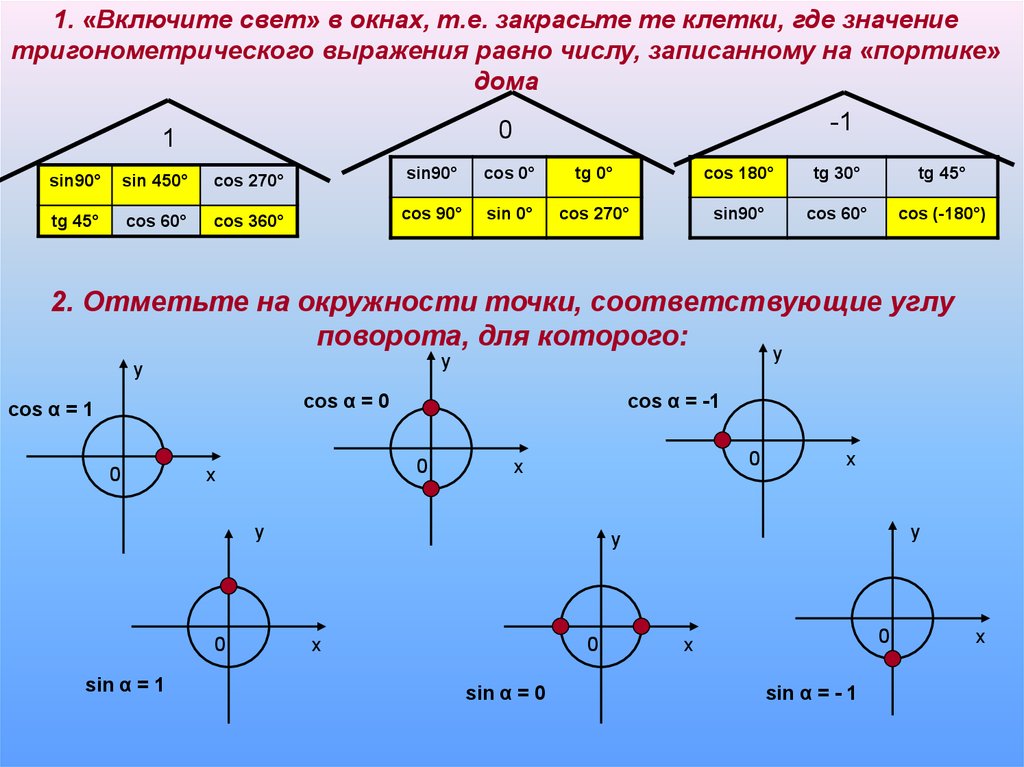
23.
1. «Включите свет» в окнах, т.е. закрасьте те клетки, где значениетригонометрического выражения равно числу, записанному на «портике»
дома
-1
0
1
sin90°
sin 450°
cos 270°
sin90°
cos 0°
tg 0°
cos 180°
tg 30°
tg 45°
tg 45°
cos 60°
cos 360°
cos 90°
sin 0°
cos 270°
sin90°
cos 60°
cos (-180°)
2. Отметьте на окружности точки, соответствующие углу
поворота, для которого:
у
у
у
cos α = 0
cos α = 1
0
cos α = -1
0
х
0
х
у
0
sin α = 1
х
у
у
х
0
sin α = 0
0
х
sin α = - 1
х



![Синус , косинус, тангенс и котангенс угла из промежутка [0°; 180°] Синус , косинус, тангенс и котангенс угла из промежутка [0°; 180°]](https://cf.ppt-online.org/files/slide/3/3kQr0l6O1wNREX7d5nJc9yFWiHCfveoLTPmKqh/slide-4.jpg)


 mathematics
mathematics