Единичная окружность

1.

2.

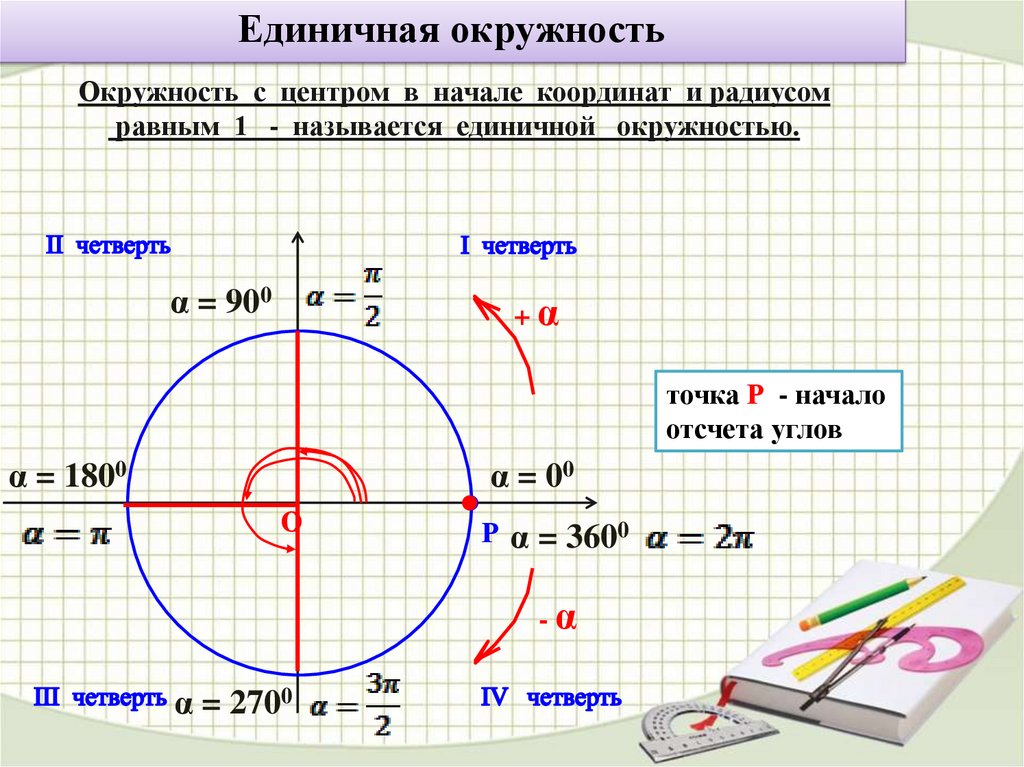
Единичная окружность
Окружность с центром в начале координат и радиусом
равным 1 - называется единичной окружностью.
α = 900
+α
точка Р - начало
отсчета углов
α = 1800
α = 00
О
Р α = 3600
-α
α = 2700

3.

Единичная окружность
Окружность с центром в начале координат и радиусом
равным 1 - называется единичной окружностью.
α = -2700
α = -1800
точка Р - начало
отсчета углов
α = 3600
О
Р α = 00
-α
α = -900

4.

Единичная окружность
α = 900
точка Р - начало
отсчета углов
+α
α = 1800
α = 00
О
Р α = 3600
-α
α = 2700
Задание устно: Определить четверть в которой лежит угол
π
12
-150 0
125 0
2100
3π
4
7π
4
3900
-45 0
3300
7π
8
4600
- 300 0
-1200
-250 0

5.

Координаты точки на единичной окружности
900
А (0;1)
=
Р (1;0)
В (-1;0)
1800
00
О
=
2700 =
3600=
С (0;-1)
Точке А (0,1)
соответствую углы:
900
900+3600
900+3600 +3600 +…
900-3600
900-3600 -3600 -…
Или в радианах:

6.

Координаты точки на единичной окружности
А (0;1)
900 =
М
Р (1;0)
В (-1;0)
00
О
1800 =
2700 =
1. Каждому углу
3600=
С (0;-1)
соответствует единственная точка на окружности
2. Одной и той же точке на окружности соответствует
бесконечное множество углов
где к – целое число

7.

Определение синуса и косинуса
B
Δ
ОМА :
ОМ 1
ОА х;
АМ ОВ у
cos х
sin у
cos
OА х
х
OМ 1
sin
AМ у
у
OМ 1
По теореме Пифагора :
sin 2 cos 2 1
M cos ; sin
B
y
x
A
cos
sin
ctg
tg
sin
cos

8.

у
О
с
ь
-1
с
и
н
у
с
о
в
Окружность радиуса 1 с центром в
М (x; y) начале координат, на которой
1
задана точка М — начало отсчета
для измерения углов,
+
и направление
α 1 М (1;0) положительного обхода,
х
называется единичной
Ось
косинусов
0
(тригонометрической)
окружностью
̶
sin α = у
Синусом угла α называется
ордината (у) точки,
полученной поворотом точки
(1; 0) вокруг
Косинусом угла α называется абсцисса
(х) начала
точки,
координат
угол α
полученной поворотом точки (1;
0) вокругна
начала
координат на угол α
̶1
cos α = x
Для любого угла α существует:
1) синус этого угла и притом единственный;
2) косинус этого угла и притом единственный
Значит, есть
функции
sin α и cos α

9.

cos
cos
cos
cos
180
270
90
0000===10
–1
0
sin
sin
sin
sin
270
180
90
00000===0–1
10
y
1
π
—
90o 2
(0;1)
Используя точку,
соответствующую
углу α, запишите
синус и косинус угла,
+
sin α = у
π180o ( ̶ 1;0)
-1
cos α = x
(1;0) 0o 0
1 360o
2πx
0
(0; ̶ 1) -1
270o3π
—
2

10.

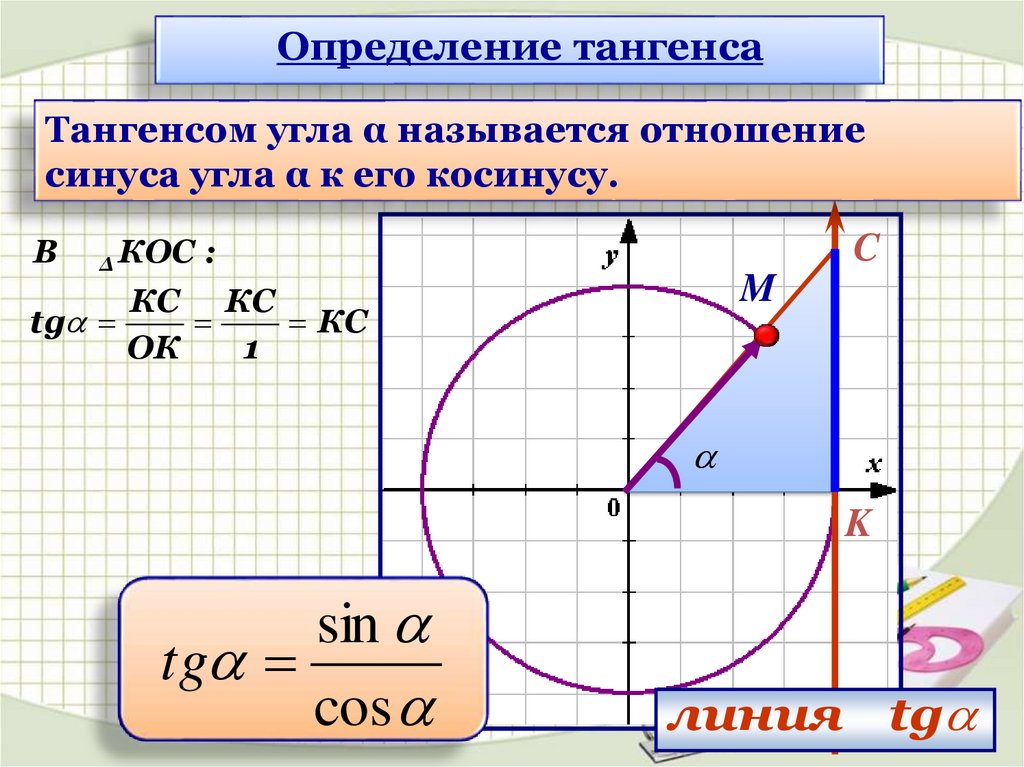
Определение тангенса
Тангенсом угла α называется отношение
синуса угла α к его косинусу.
В
Δ
КОС :
C
M
КС КС
tg
КС
ОК
1
K
sin
tg
cos
линия tg

11.

Определение котангенса
Котангенсом угла α называется отношение
косинуса угла α к его синусу.
линия сtg
В
ΔODN :
ctg
N
D
NД NД
NД
ОN
1
cos
сtg
sin
M

12.

Значения синуса и косинуса
60°
3
22
45°
30°
2
1
2
1 2 3
2 2 2

13.

14.

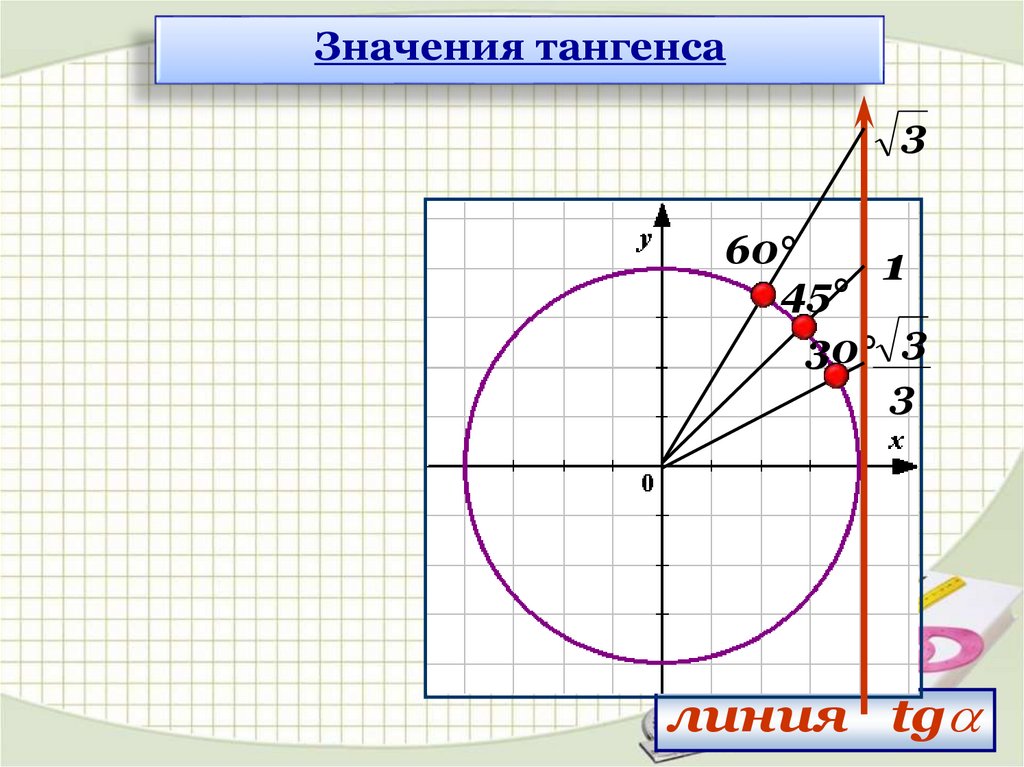
Значения тангенса
3
60°
1
45°
30° 3
3
линия tg

15.

Значения котангенса
3
3
линия сtg
60°
1
45°
30°
3

16.

Значения тригонометрических
функций для некоторых углов
2 90
2
120
3
1
60
3
5
6 150
6
30
180
0
-1
1360 2
11
330 6
210
7
6
240
4
3
3
2
-1270
300
5
3

17.

Значения тригонометрических
tg 3
функций для некоторых углов
3
3
3
3
3
1
3
2
30
2
2
5
150
6
3
3
3
1
2
6
0
-1 23
2
2
1
2
1
sin150 7 sin30
2
6 210
1
2
1
2
2
2
3
2
3
cos150 cos30
2 -1
2
2
3
2
1
11
330 6
3
3
3
ctg

18.

Значения тригонометрических
3
tg
функций для некоторых углов
3
2
3
3
3
1
120
3
2
3
3
60
3
3
2
2
3
3
1
2
0
-1
3 2
2
2
sin120 sin60
1
2
3
2
1
2
2
2
3
2
2 3
2 2
1
1
240
cos120 cos604
3
1
2
2
-1
5
3
300
3
3
3
ctg

19.

Значения тригонометрических
tg
функций для некоторых углов
2 90
-1
3
4
135
180 -1
sin135 sin45
1
1
ctg
45
4
2
2
0 360
2
2
2
2
2
2
5 225 2
cos135 cos45
4
2
2
2
315 7
270
-1
1 2
3
2
4
-1

20.

21.

Найти все значения синуса и косинуса числа
β
3π
3,5π
Cos β
-1
0
0
-1
Sin β
β
, если:
πk
1; -1
0

22.

Выполнить задания из учебника
№ 432(а,б), 434, 437