Многоугольники (полигоны)

1. Многоугольники (полигоны)

Тесты ориентации точки
относительно полигона

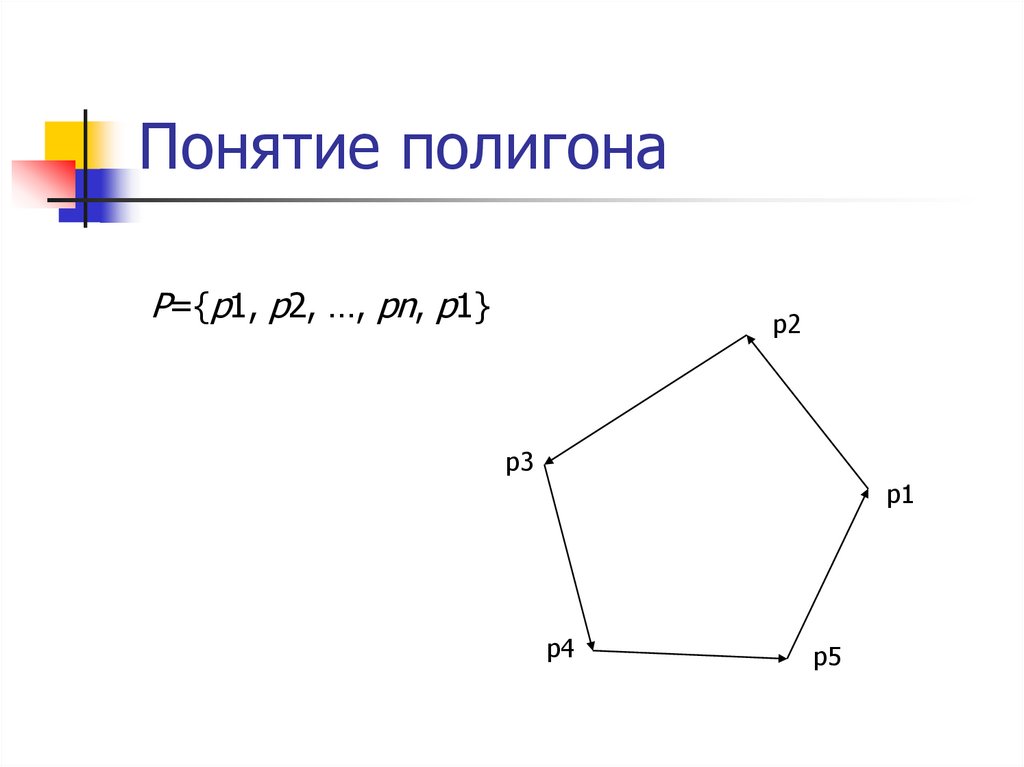
2. Понятие полигона

P={p1, p2, …, pn, p1}
p2
p3
p1
p4
p5

3.

Свойства плоских многоугольников

4. Пересечение прямой линии с полигоном

Прямая пересекает полигон, если существует хотя бы
одна пара вершин, лежащих от нее по разные
стороны
Cравнение выполняется для всех имеющихся пар
вершин, а не только смежных

5. Пересечение прямой линии с полигоном

p2
p3
p1
p4
p5

6. Выпуклость полигона

У выпуклого полигона все углы (pi-1 pi pi+1)
одного знака
При обходе выпуклого полигона по замкнутому
контуру в произвольном направлении каждая
вершина p i+1 расположена относительно ребра (pi1 pi ) одинаково для всех значений i : слева при
положительном направлении обхода и справа при
отрицательном

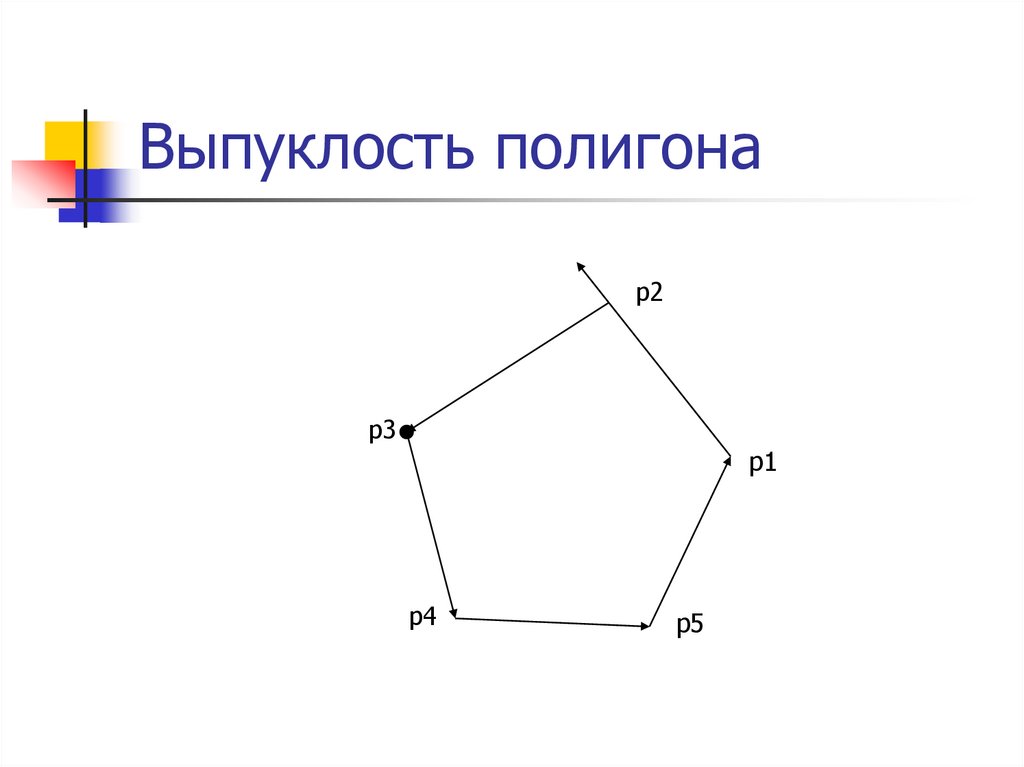
7. Выпуклость полигона

p2
p3
p1
p4
p5

8. Самопересечение полигона

Полигон является самопересекающейся замкнутой
ломаной линией, если у него существует хотя бы
одна пара пересекающихся отрезков
Тестироваться должны все пары несмежных ребер
полигона

9. Самопересечение полигона

10.

Тесты ориентации точки
относительно полигона

11. Габаритный тест

Определяет гарантированную
непринадлежность точки q произвольному
полигону P
Полностью задачу ориентации не решает
Применяется во многих алгоритмах для
быстрого обнаружения заведомо
непересекающихся геометрических
объектов

12. Габаритный тест

q .
ymax
ymin
xmin
xmax

13. Выпуклый тест

Определяет положение точки относительно
полигона: внешняя точка, внутренняя точка,
граничная точка
Внешнее подпространство полигона считается
положительным, внутреннее – отрицательным,
граница соответствует нулю

14. Выпуклый тест

p4
+
. qвнеш
_
_
p5
+
. qвн
+
p3
. qгр
_
_
p1
_
+
p2
+

15. Угловой тест (радианный)

Основан на вычислении и анализе
алгебраической суммы углов i = (Vi , Vi+1 )
между смежными векторами Vi =pi - q,
соединяющими точку q с вершинами pi ,
при обходе произвольного полигона P
по замкнутому контуру в произвольном
направлении.

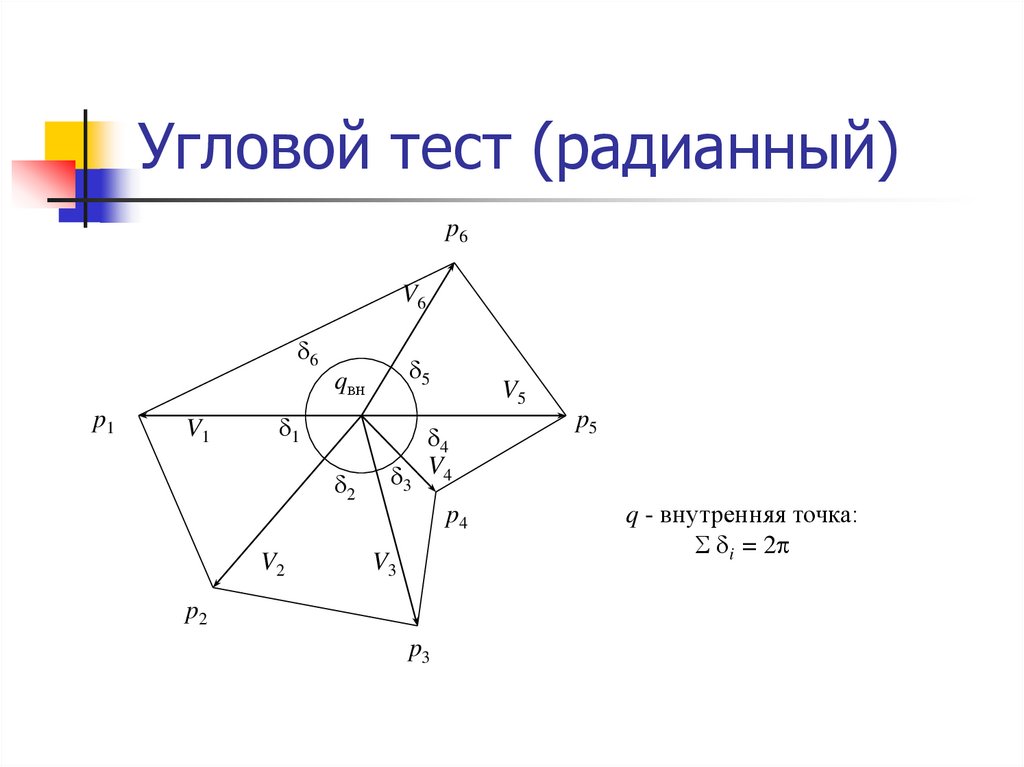
16. Угловой тест (радианный)

p6
V6
6
5
qвн
p1
V1
1
2
V2
4
3 V4
p4
V3
p2
p3
V5
p5
q - внутренняя точка:
i = 2

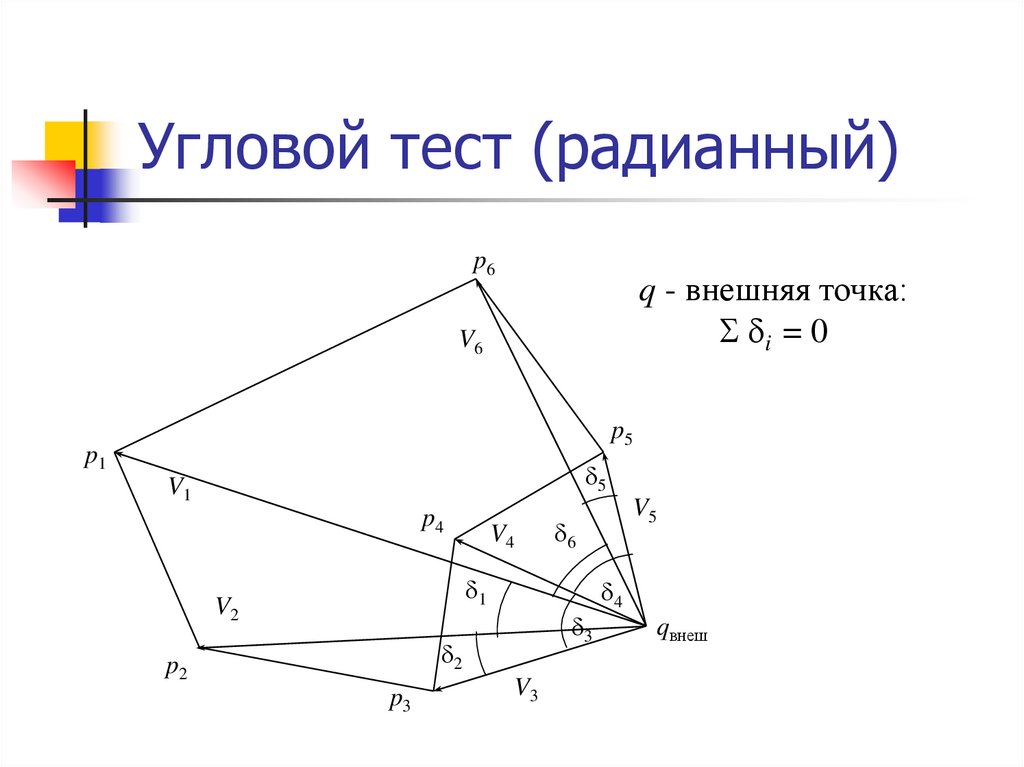
17. Угловой тест (радианный)

p6
q - внешняя точка:
i = 0
V6
p5
p1
5
V1
p4
6
V4
1
V2
3
2
p2
p3
V5
V3
4
qвнеш

18. Угловой тест (радианный)

Точка является внутренней, если сумма углов
∑ i=2 π
Точка является внешней, если сумма углов ∑ i=0
Точка является граничной:
- если при расчете векторов получен нулевой вектор
Vi =0, то тестируемая точка совпадает с вершиной
pi ;
- если при расчете углов i получен развернутый
угол с модулем | i | = π, то тестируемая точка
лежит на ребре (pi pi+1)

19. Лучевой тест

Заключается в выпускании из этой точки в
произвольном направлении V луча p(t)=q+Vt
(
t > 0) и подсчете числа его пересечений с ребрами
p
Исследуются параметры пересечения луча с
отрезками pi +(pi+1 –pi) , 0 1.

20. Лучевой тест

− точка является внутренней, если число пар
нечетно (ti >0, 0< i <1);
− точка является внешней, если число пар четно, в
том числе равно нулю;
− точка лежит на границе, если найдется хотя бы
одна пара, для которой ti =0, 0 i 1

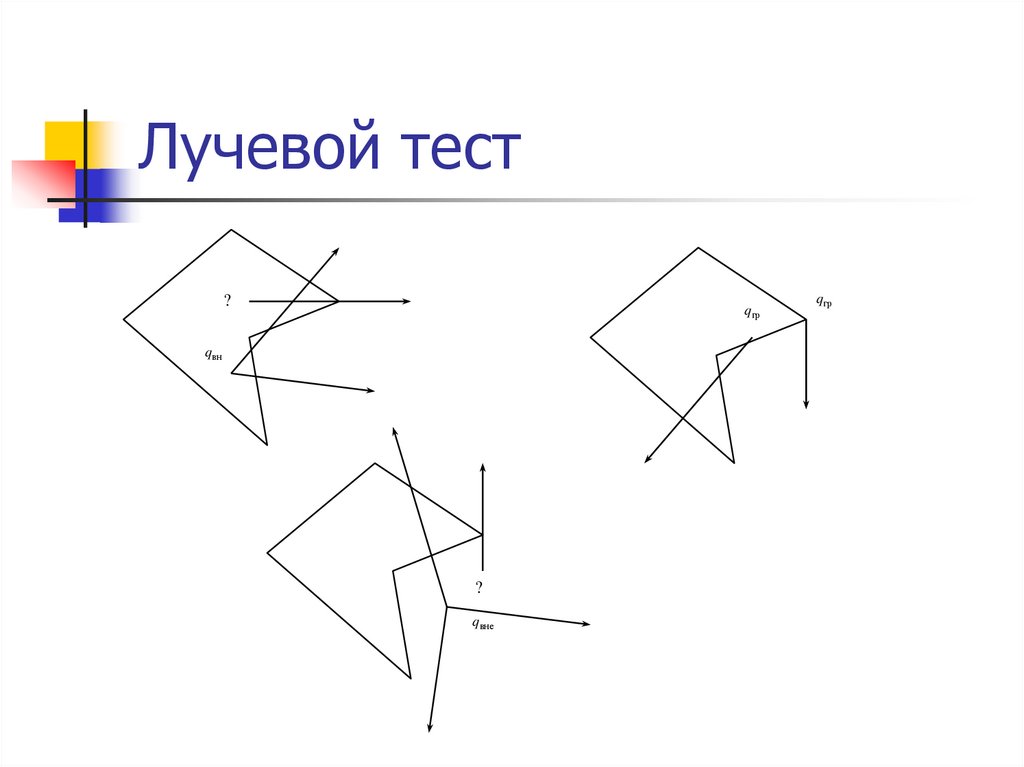
21. Лучевой тест

?
qгр
qвн
?
qвне
qгр

22. Лучевой тест

Особенности лучевого теста:
требуется расчет параметров
пересечения луча со всеми ребрами
полигона
неопределенность числа пересечений
при прохождении луча точно через
вершину pi при i=1 или вершину pi+1 при
i =0. (необходимо повторить тест
заново с другим направлением луча V)