Similar presentations:
Основные понятия математической статистики. Математическая статистика
1. Математическая статистика
2. Основные понятия математической статистики
3.
Математическая статистика (МС) – это наука,занимающаяся разработкой методов получения,
описания и обработки опытных данных с целью
изучения закономерностей массовых, случайных
явлений.
Установление
закономерностей,
которым
подчинены массовые случайные явления, основано
на изучении статистических данных, то есть на
результатах наблюдений.
4. Задачи математической статистики
Первая задача МС – разработка способов сбора игруппировки статистических данных (если данных
очень много).
Вторая задача МС – разработка методов анализа
статистических данных в зависимости от целей
исследования.
5.
Типичными задачами математической статистикиявляются:
1) определение закона распределения случайной
величины по статистическим данным;
2) статистическая проверка гипотез;
3)
нахождение
неизвестных
параметров
известного закона распределения.
6. Генеральная и выборочная совокупности
7.
Генеральнойсовокупностью
называется
совокупность значений исследуемого признака.
Общее число объектов генеральной совокупности
называется объемом генеральной совокупности N.
Выборочной
совокупностью
(выборкой)
называется совокупность случайно отобранных
объектов из генеральной совокупности.
Объем выборки обозначается n. Причем n N.
8.
Например, в партии из 1000 деталей отобрано дляобследования 100 деталей. На основе обследования
100 деталей судят о качестве деталей всей партии.
Тогда в данном примере объем генеральной
совокупности N = 1000, а объем выборки n = 100.
Выборочный метод заключается в том, что из
генеральной совокупности извлекается выборка
объема n, определяются характеристики, которые
принимаются в качестве приближенных оценок
соответствующих
характеристик
генеральной
совокупности. При n N выборочная совокупность
приближается к генеральной.
9.
Выборки подразделяют на:1) повторная, при которой отобранный объект перед
отбором следующего возвращается в генеральную
совокупность;
2) бесповторная, при которой отобранный объект в
генеральную совокупность не возвращается.
На практике обычно пользуются бесповторным
случайным отбором.
Основным требованием к выборке является
репрезентативность (представительность) выборки.
Выборка будет репрезентативной, если каждый
объект выборки отобран случайно из генеральной
совокупности, и этом все объекты имеют одинаковую
вероятность попасть в выборку.
10. Статистическое распределение выборки
11.
Пустьиз
генеральной
совокупности
извлечена
выборка, причем x1 наблюдалось n1 раз, x2 – n2 раз, xk – nk
раз. Причем
k
n n, где n – объем выборки.
i 1
i
Наблюдаемые значения xi называются вариантами, а
последовательность вариант, расположенная в порядке
возрастания называется вариационным рядом.
Числа наблюдений вариант ni называются частотами,
а их отношения к объему выборки называются
относительными частотами: p* ni .
i
n
12.
Статистическимраспределением
выборки
называется перечень вариант и соответствующих им
частот:
или относительных частот:
13.
Статистическое распределение выборки можетбыть задано и в виде последовательности
интервалов и соответствующих им частот или
относительных частот:
X
(xmin; x1)
(x1; x2)
(x2; x3)
…
(xk-1; xmax)
n
n1
n2
n3
…
nk
где (xi; xi-1) называется интервалом (частичным
интервалом), величина hi = xi - xi-1 длина i-го
интервала.
значения xmin, x1, x2 ,…, xk-1, xmax называются
границами интервалов.
14.
Для учета границ интервалов при определениичастоты
попадания
в
заданный
интервал
формируются следующие правила отнесения
вариант:
xi 1 x xi
или
xi 1 x xi
В первом случае границы интервалов относятся к
левому частичному интервалу, а во втором – к
правому. Величины частичных интервалов могут
быть как одинаковой длины, так и разной.
15. Статистическая функция распределения
16.
Пусть nx – число наблюдений, при которыхзначение наблюдаемого признака (объекта) меньше
некоторого значения Х. Тогда относительная частота
события Х < х определяется соотношением:
nx
*
Px .
n
Статистической
(эмпирической)
функцией
распределения называется функция, определяющая
для каждого значения х относительную частоту
nx
*
события Х < х, то есть F ( x) , где nx – число
n
вариант меньше Х, n – объем выборки.
17.
Функцияраспределения
F(x)
генеральной
совокупности называется теоретической функцией
распределения.
Различие между F(x) и F*(x) состоит в том, что F(x)
определяет вероятность события Х<х, а F*(x) –
относительную частоту этого события.
График F*(x) представляет собой ступенчатую
функцию, аналогичную графику теоретической функции
F(x), скачки которой соответствуют вариантам и по
величине равны относительным частотам этих вариант.
18.
Статистическая (эмпирическая) функция распределенияF*(x) обладает всеми свойствами функции F(x) для
дискретной случайной величины.
1) Значения эмпирической функции распределения F*(х)
принадлежат отрезку [0; 1].
2) Функция F*(х) – неубывающая функция.
3) Если х1 – наименьшая варианта, то F*(х) =0 при х х1,
если хk – наибольшая варианта, то F*(х) =1 при х > хk.
Статистическая (эмпирическая) функция распределения
выборки служит для оценки теоретической функции
распределения генеральной совокупности.
19.
Пример. Задано распределение частот выборки.Найти распределение относительных частот,
статистическую
функцию
распределения
и
построить ее график.
xi
2
6
12
ni
3
10
7
Решение:
Найдем относительные частоты рi*, для чего
разделим частоты на объем выборки n:
3
n ni 3 10 7 20.
i 1
20.
3p
0,15;
20
*
1
10
p
0,5;
20
*
2
7
p
0,35.
20
*
3
Запишем распределение относительных частот:
xi
pi*
2
0,15
6
0,5
12
0,35
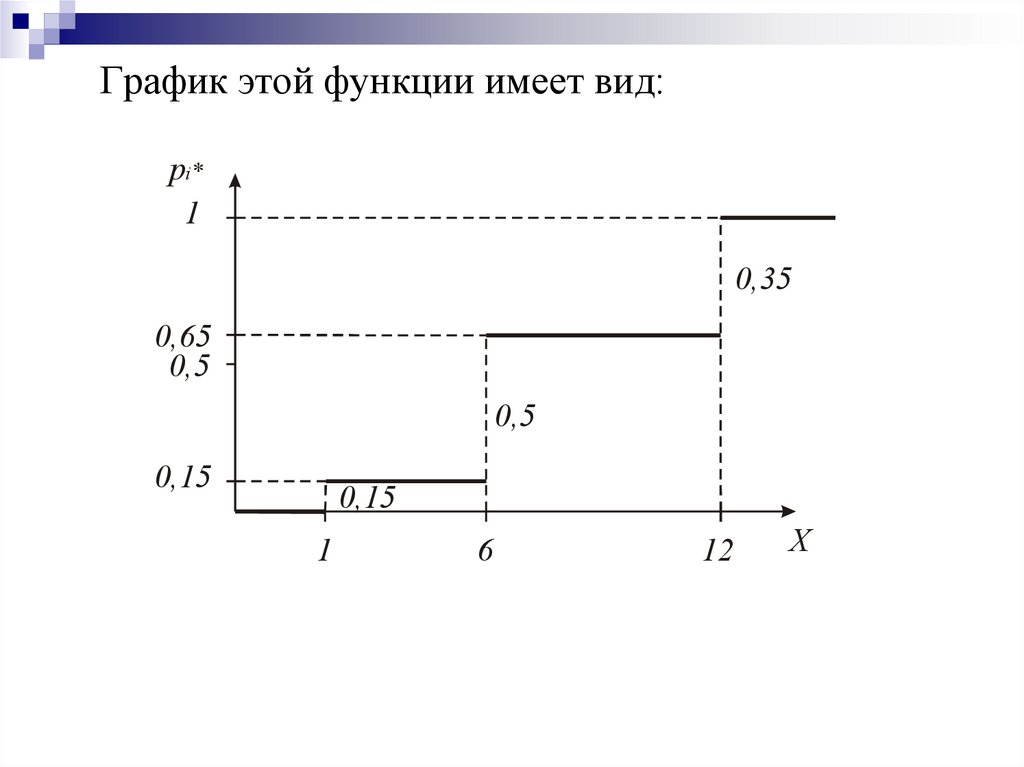
Найдем статистическую функцию распределения:
x 2;
0,
0,15, 2 x 6;
*
F ( x)
0,65, 6 x 12;
1,
x 12.
21.
График этой функции имеет вид:pi*
1
0,35
0,65
0,5
0,5
0,15
0,15
1
6
12
X
22. Полигон и гистограмма статистического распределения
23.
Для наглядности представления статистическогораспределения выборки строят различные графики. К
таким графикам относятся полигон и гистограмма.
Полигоном частот называется ломаная линия,
отрезки которой соединяют точки: (x1, n1), (x2, n2), …,
( xk, nk).
Полигоном относительных частот называется
ломаная линия, отрезки которой соединяют точки
(x1,p1*), (x2, p2*),…,( xk, pk*).
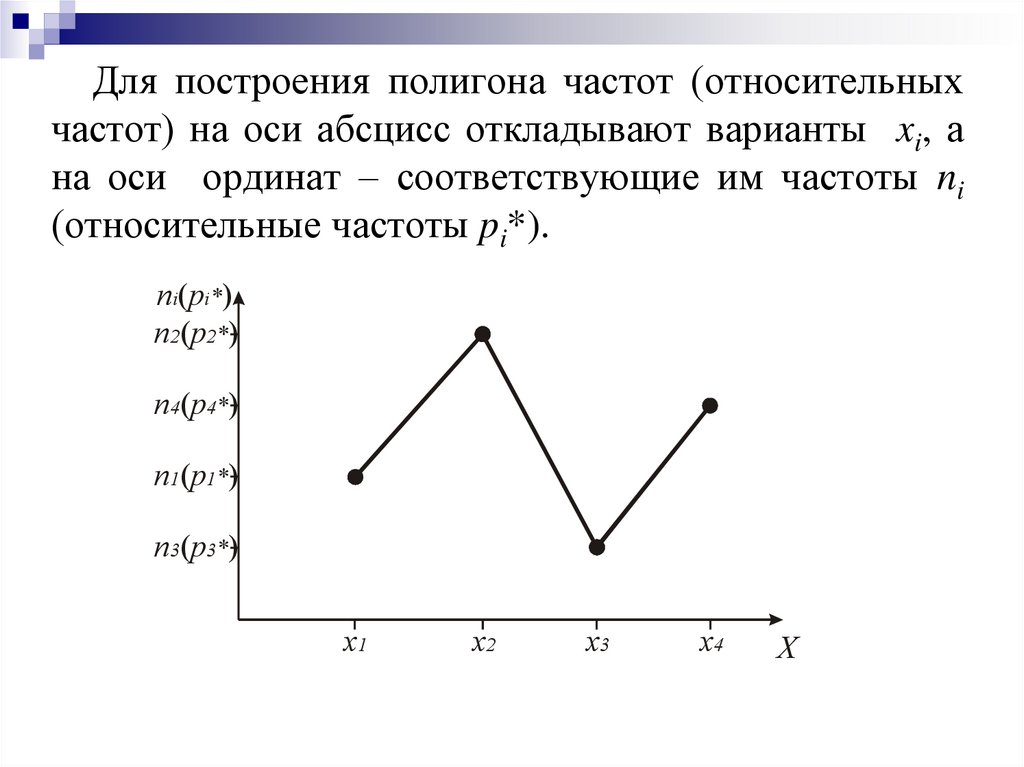
24.
Для построения полигона частот (относительныхчастот) на оси абсцисс откладывают варианты xi, а
на оси ординат – соответствующие им частоты ni
(относительные частоты pi*).
ni(pi*)
n2(p2*)
n4(p4*)
n1(p1*)
n3(p3*)
x1
x2
x3
x4
X
25.
Полигон можно строить и для статистическогораспределения
заданного
последовательностью
интервалов. В этом случае, в каждом интервале
выбирается одна варианта, в качестве которой могут
использоваться:
• левые границы интервалов;
• правые границы интервалов;
• середины интервалов (чаще всего).
Если величины интервалов постоянны и равны между
собой, то значения x1*, x2*, …, xk* называют
равноотстоящими вариантами.
26.
Гистограммой частот (относительных частот)называют ступенчатую фигуру, состоящую из
прямоугольников, основаниями которых служат
частичные интервалы статистической совокупности,
представленной в виде последовательности частичных
интервалов длиною h, а высоты равны плотности
*
n
h
p
частоты i
(плотности относительной частоты i h ).
Площадь гистограммы частот равна сумме всех
частот, то есть объему выборки.
Площадь гистограммы относительных частот равна
сумме всех относительных частот, то есть единице.
Гистограмма строится, как правило, для выборки
большой размерности.
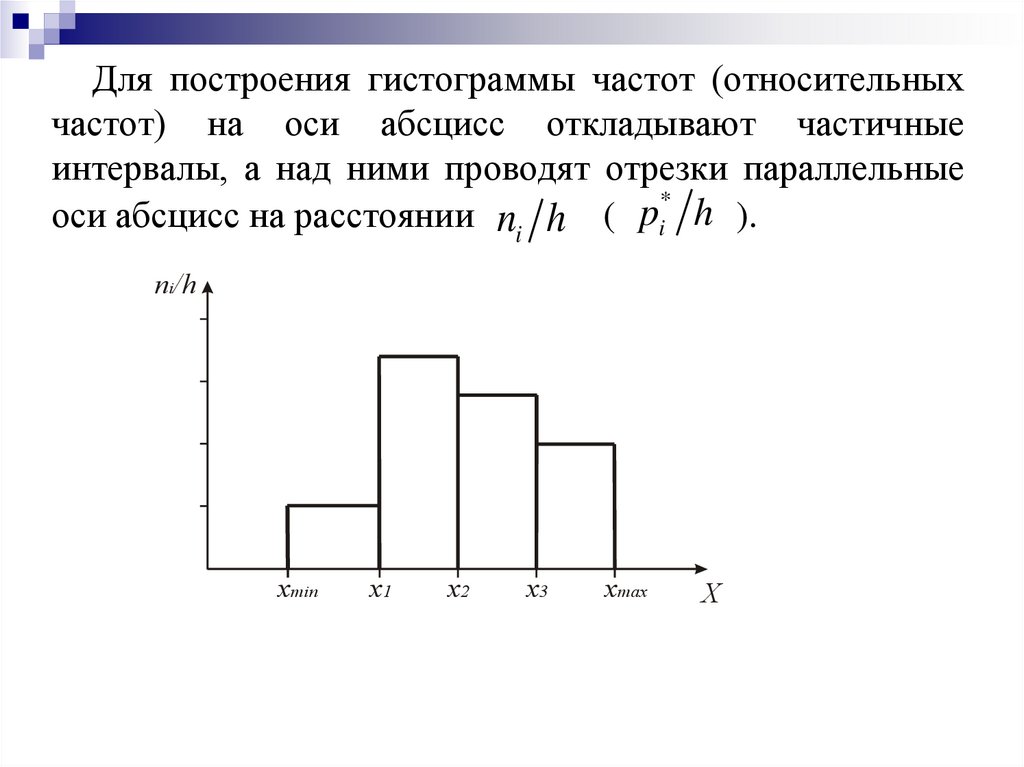
27.
Для построения гистограммы частот (относительныхчастот) на оси абсцисс откладывают частичные
интервалы, а над ними проводят отрезки параллельные
*
p
оси абсцисс на расстоянии ni h ( i h ).
ni/h
xmin
x1
x2
x3
xmax
X
28.
Наглядность гистограммы зависит от числачастичных интервалов k, определяемых по формуле:
xmax xmin
k
.
h
При этом число интервалов обычно определяется из
условия kmin 5.
На практике k часто определяется из условия k n.
29.
Пример. Известны урожайности в центнерах на одингектар яровой пшеницы в 20 хозяйствах: 13,9; 12,4; 13,1;
6,3; 11,8; 11,6; 10,5; 10,4; 10,6; 11,3; 15,1; 11,7; 11,3; 10,2;
11,0; 10,7; 8,2; 9,6; 10,2; 15,1. Получить интервальный ряд
распределения и начертить гистограмму относительных
частот.
Решение:
Запишем исходные данные в виде вариационного ряда:
6,3; 8,2; 9,6; 10,2; 10,2; 10,4; 10,5; 10,6; 10,7; 11,0; 11,3;
11,3; 11,6; 11,7; 11,8; 12,4; 13,1; 13,9; 15,1; 15,1.
Диапазон изменения составляет от 6 до 16. Разобьем
диапазон на несколько частичных интервалов.
Так как k 20 , то выберем k=5.
30.
Число частичных интервалов равно 5, тогда длиначастичного интервала равна h 16 6 2.
5
Таким образом, получили 5 интервалов:
(6; 8), (8; 10), (10; 12), (12; 14), (14; 16).
Определим частоту попадания вариант в каждый
частичный интервал: n1 = 1; n2 = 2; n3 = 12; n4 = 3; n5 = 2.
Определим относительные частоты:
1
2
16
*
*
p
0,05, p2
0,1, p3
0,6,
20
20
20
3
2
p4*
0,15, p5*
0,1.
20
20
*
1
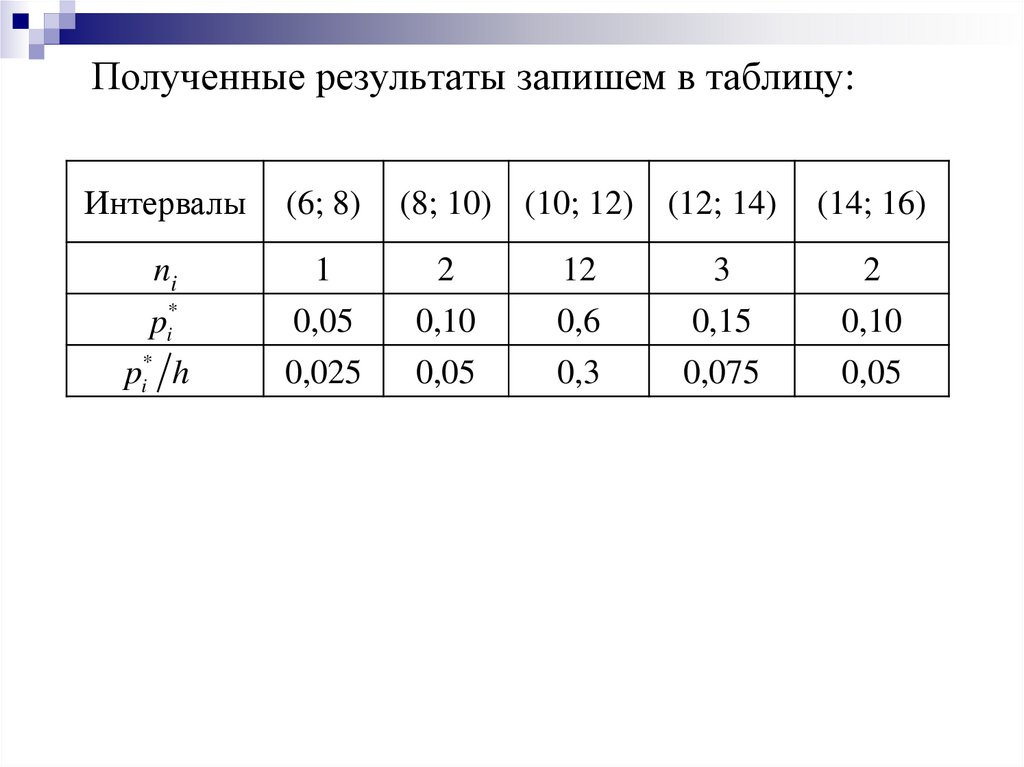
31.
Полученные результаты запишем в таблицу:Интервалы
(6; 8)
(8; 10) (10; 12) (12; 14)
ni
1
0,05
2
0,10
12
0,6
3
0,15
2
0,10
0,025
0,05
0,3
0,075
0,05
pi*
pi* h
(14; 16)
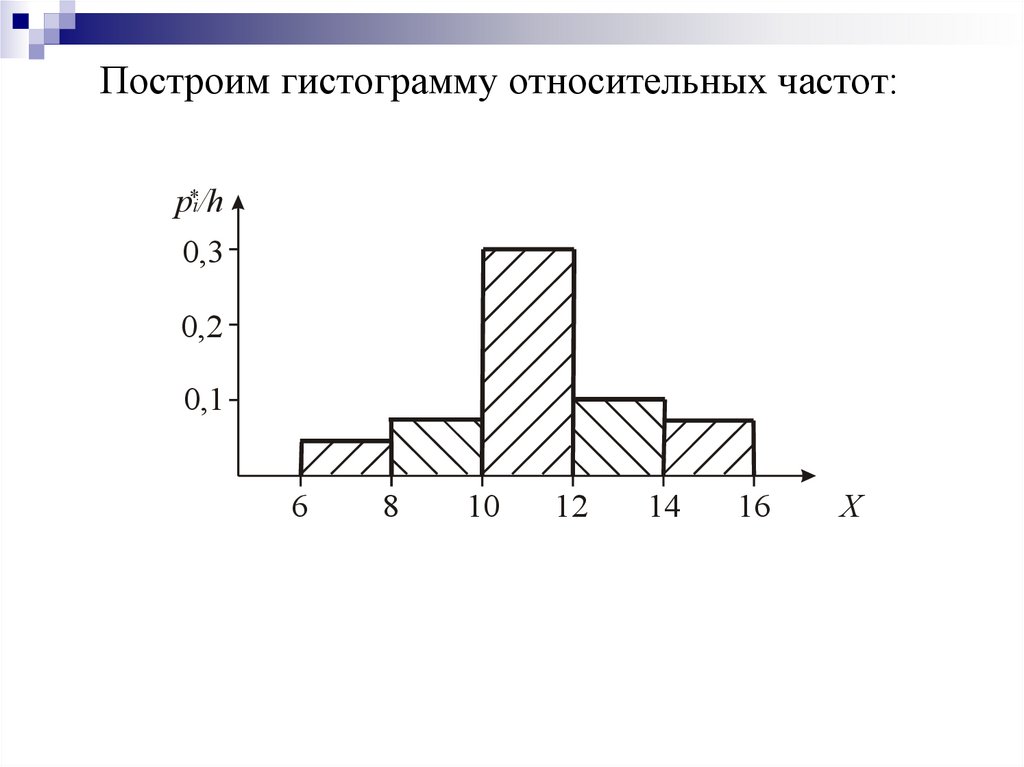
32.
Построим гистограмму относительных частот:p*i/h
0,3
0,2
0,1
6
8
10
12
14
16
X



























 mathematics
mathematics








