Математическая статистика. (Лекция 7)

1. Математическая статистика

Основные понятия

2. Вариационные ряды

Множество всех объектов, подлежащих исследованию, называют
генеральной совокупностью. Множество объектов, случайным образом
отобранных из генеральной совокупности, называется выборкой.
Объемом совокупности (генеральной или выборочной) называют
число объектов этой совокупности.
Последовательность результатов наблюдения
1
2
m
x , x , , x
записанных в порядке неубывания, т.е.
x1 x2 xm
называется вариационным рядом.
Если варианты
x1 , x2 , , xm
при наблюдении встретились соответственно
то числа
n1 , n2 , , nm
Если объем выборки равен п, то
n1 , n2 , , nm
называются частотами.
n1 n2 nm n
раз,

3.

Статистическая таблица частот
Варианты
xi
Частоты
ni
x1
n1
x2
n2
xm
nm
Отношения частот к объему выборки
nm
n1 n2
, , ,
n n
n
называются относительными частотами.
Статистическая таблица относительных частот
Варианты
xi
Относительные
частоты
ni
n
x1
x2
n1
n
n2
n
xm
nm
n

4.

Провели следующий эксперимент. Книгу открывали на случайной
странице, где выбирали случайное слово. При этом фиксировали
длину слова. В результате 20 опытов получена следующая выборка:
4, 1, 4, 5, 1, 13, 4, 10, 2, 4, 7, 2, 2, 4, 6, 4, 5, 6, 2, 4.
Ей соответствует вариационный ряд:
1, 1, 2, 2, 2, 2, 4, 4, 4, 4, 4, 4, 4, 5, 5, 6, 6, 7, 10, 13.
Статистическая таблица частот
xi
1
2
4
5
6
7
10
13
ni
2
4
7
2
2
1
1
1

5.

Статистическая таблица относительных частот
xi
ni
n
1
2
4
5
6
7
10
13
0,1
0,2
0,35
0,1
0,1
0,05
0,05
0,05

6.

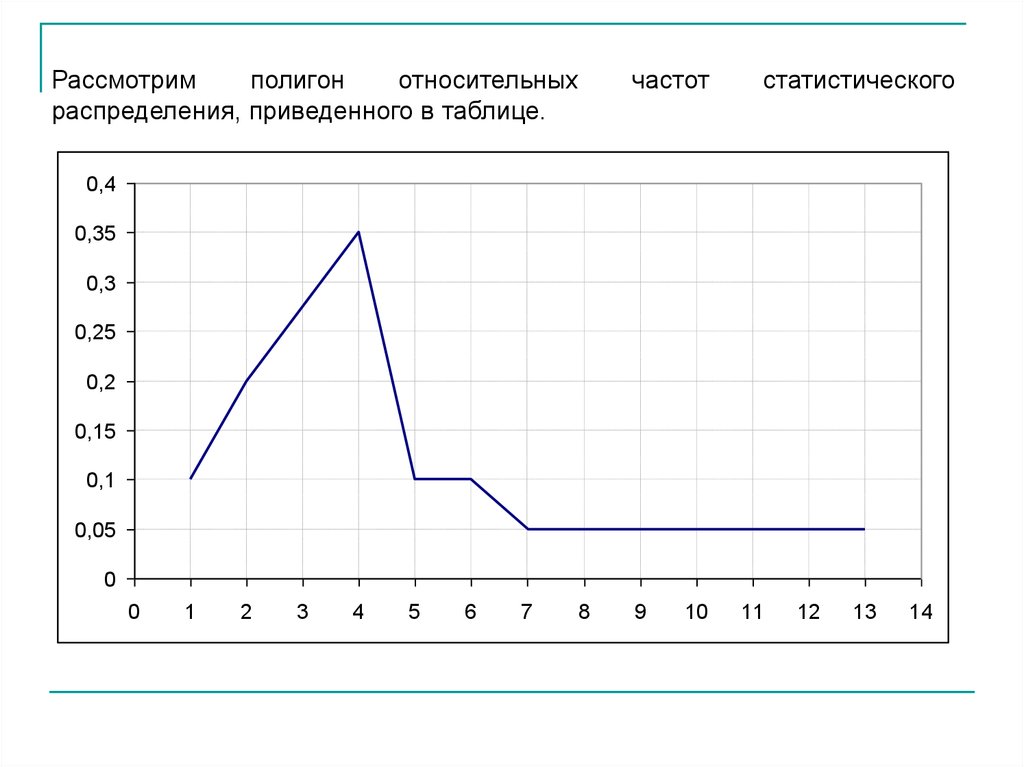
Рассмотрим
полигон
относительных
распределения, приведенного в таблице.
частот
статистического
0,4
0,35
0,3
0,25
0,2
0,15
0,1
0,05
0
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14

7.

Во многих задачах значения признака разбивают на группы.
Статистическое распределение выборки задают в виде
последовательности интервалов и соответствующих им частот. В
качестве частоты, соответствующей интервалу, принимают сумму
частот вариант, попавших в этот интервал.
Если каждое значение частоты разделить на длину
соответствующего интервала, то полученные числа
nm
n1 n2
, , ,
l1 l 2
lm
называют плотностями частот.
li

8.

Если каждое значение относительной частоты разделить на длину
li
соответствующего интервала, то полученные числа
nm
n1
n2
,
, ,
n l1 n l 2
n lm
называют плотностями относительных частот.
Для наглядности изображения статистической таблицы строят
ступенчатую фигуру, состоящую из прямоугольников, в основании
которых лежат интервалы, а высотами являются соответствующими
им плотности частот или относительные плотности частот.

9.

Гистограммой частот называется ступенчатая фигура, состоящая из
прямоугольников с основанием
h xi xi 1
ni
h
и высотами
На оси абсцисс откладывают частичные интервалы длиной h, на i-м
интервале строят прямоугольник высотой
ni
h
(плотность частоты).
Площадь S гистограммы частот равна сумме всех частот, т.е. объему
выборки.
Действительно, если
S i – площадь прямоугольника, то
ni
S i h ni
h
k
k
i 1
i 1
S S i ni n

10.

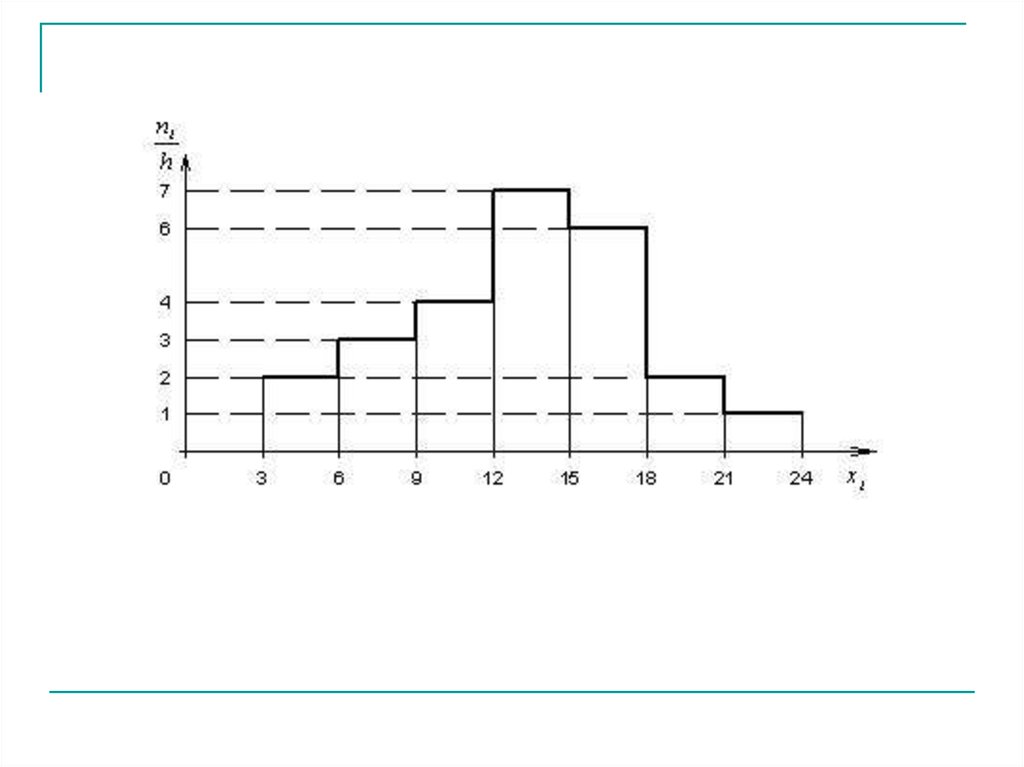
Приведем гистограмму частот распределения объема п = 75, указанного
в таблице.
nnii
h
Частичный
интервал длины
h=3
Сумма частот
частичного
интервала ni
Плотность
частоты
ni
h
[3; 6]
(6; 9]
(9; 12]
(12;15]
(15; 18]
(18; 21]
(21; 24]
6
9
12
21
18
6
3
2
3
4
7
6
2
1

11.

12. Эмпирическая функция распределения

Эмпирической функцией распределения (функцией распределения
выборки) называется функция
F * x
определяющая для каждого значения х частоту события
Пусть
nx
X x
– число вариант, меньших х, п – объем выборки. Тогда
nx
F * x
n

13.

Из определения эмпирической функции
1. Значения функции
2.
F * x
F * x
F * x
следуют ее свойства:
принадлежат отрезку [0,1].
– неубывающая функция.
3. Если а – наименьшая, b – наибольшая варианта, то
F * x 0
при
F * x 1
при
4. Функция
x a
x b
F * x
непрерывна слева, так как она постоянна на полуинтервалах
xi , xi 1

14.

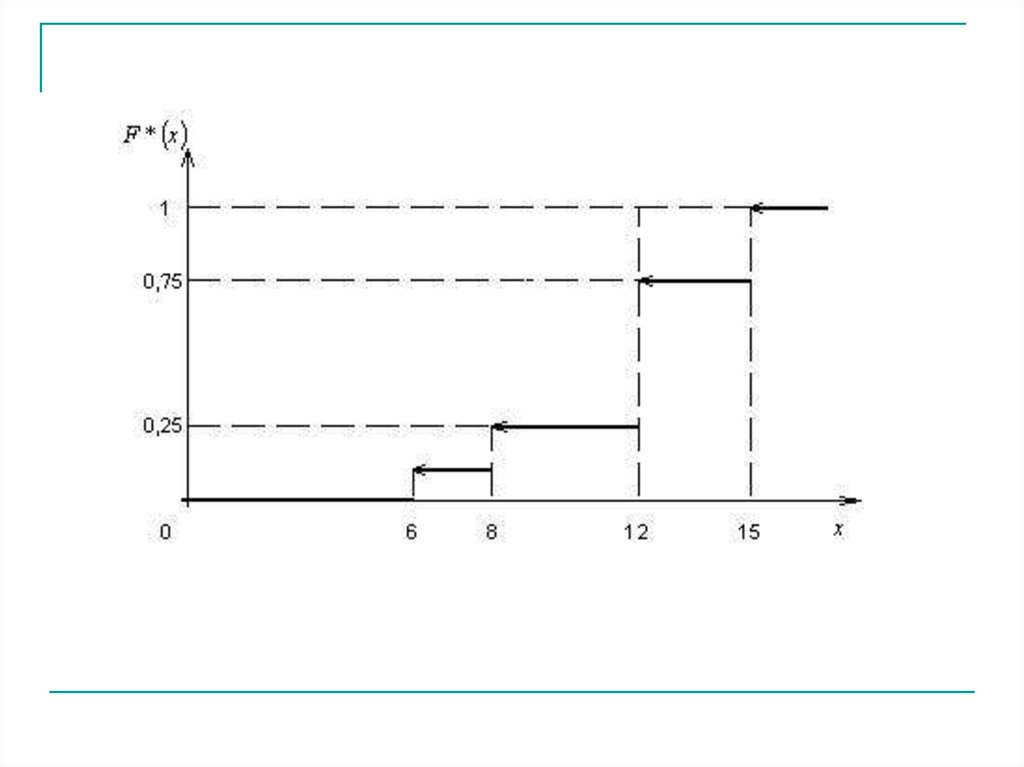
Пример 1. Построить эмпирическую функцию по данному распределению
выборки
Варианты
Частоты
xi
ni
6
8
12
15
2
3
10
5
Объем выборки
n 2 3 10 5 20
Наименьшая варианта
x1 6
x 6
Значение
X 8
x1 6
поэтому
F * x 0
если
2
F * x
0,1
20
если
наблюдалось 2 раза, поэтому
6 x 8

15.

X 12
Значения
наблюдались
если
x1 6, x2 8
2 3 5
раз, поэтому
8 x 12
Значения
X 15
наблюдались
2 3 10 15
15
F * x
0,75
20
Поскольку
F * x 1
x1 6,
x4 15
если
если
x2 8,
5
F * x
0,25
20
x3 12
раз, поэтому
12 x 15
– наибольшая варианта, то
x 15

16.

Итак, искомая эмпирическая функция определяется формулами
0
0,1
F * x 0,25
0,75
1
при x 6
при 6 x 8
при 8 x 12
при 12 x 15
при x 15

17.

18. Числовые характеристики вариационных рядов

Средним арифметическим называется постоянная, равная сумме
произведений значений признака на соответствующие значения
относительных частот
m
nm
n1
n2
x x1 x 2 x m
n
n
n
x n
i
i 1
i
n
Размахом вариации R называется разность между наибольшим и
наименьшим значениями признака
R xmax xmin

19.

Модой Мо называется значение признака, встречающееся с
наибольшей частотой, т.е. наиболее типичное в данном
вариационном ряду.
Медианой Ме называется значение признака, лежащее в середине
вариационного ряда, если этот ряд имеет нечетное число членов, и
среднее арифметическое двух значений признака, расположенных в
середине ряда, если ряд состоит из четного числа членов.

20. Статистические оценки параметров распределения

Статистическая таблица частот
Варианты
Частоты
xi
Ni
x1
N1
x2
N2
N1 N 2 N m N
xm
Nm

21.

Генеральную среднюю подсчитывают по формуле
x1 N1 x2 N 2 xm N m 1 m
xГ
xi N i
N
N i 1
а генеральную дисперсию по формулам:
1 m
2
DГ xi xГ N i
N i 1
1
1
2
DГ xi Ni xi Ni
N i 1
N i 1
m
m
2

22.

Выборочную среднюю подсчитывают по формуле
x1n1 x2 n2 xm nm 1 m
xВ
xi ni
n
n i 1
а выборочную дисперсию по формулам:
1 m
2
DВ xi xВ ni
n i 1
1
1
2
DB xi ni xi ni
n i 1
n i 1
m
m
2

23.

Выборочная дисперсия является заниженной оценкой генеральной
дисперсии. Несмещенной оценкой генеральной дисперсии является
исправленная дисперсия.
m
n
1
2
2
xi xВ ni
s
DВ
n 1
n 1 i 1

24.

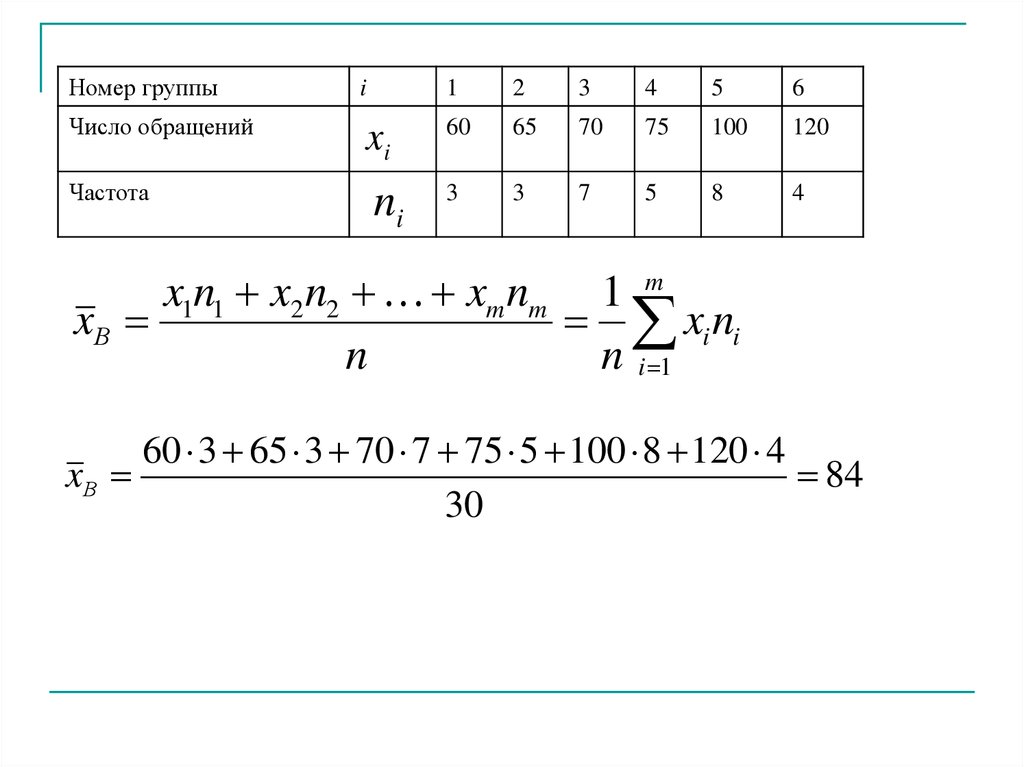
В супермаркете проводились наблюдения над числом покупателей,
обратившихся в кассу за 1 час. Наблюдения проводились в течение 30
часов (15 дней в период с 9 до 10 и с 10 до 11 часов) дали следующие
результаты:
70, 75, 100, 120, 75, 60, 100, 120, 70, 60, 65, 100, 65, 100, 70, 75, 60, 100,
100, 120, 70, 75, 70, 120, 65, 70, 75, 70, 100, 100.
Составить ряд распределения частот. Найти моду, медиану, размах
выборки. Найти выборочное среднее и несмещенную оценку
дисперсии.
Составим вариационный ряд
60, 60, 60, 65, 65, 65, 70, 70, 70, 70, 70, 70, 70, 75, 75, 75, 75, 75, 100, 100,
100, 100, 100, 100, 100, 100, 120, 120, 120, 120

25.

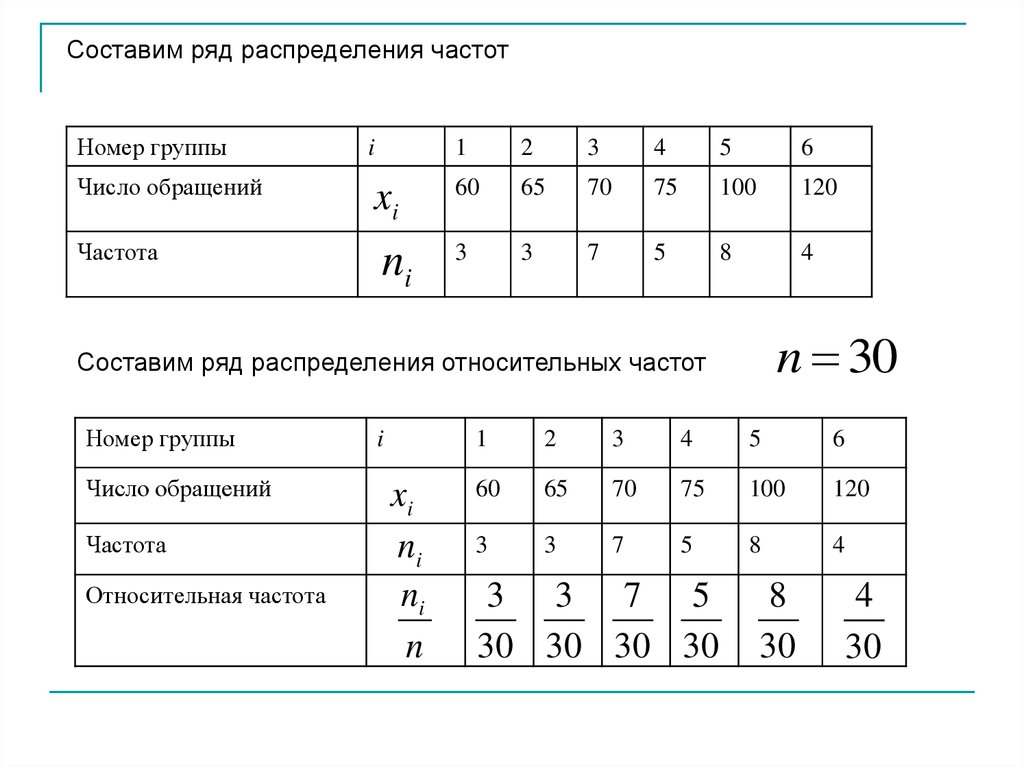
Составим ряд распределения частот
Номер группы
i
1
2
3
4
5
6
Число обращений
xi
60
65
70
75
100
120
3
3
7
5
8
4
Частота
ni
n 30
Составим ряд распределения относительных частот
Номер группы
Число обращений
Частота
Относительная частота
i
xi
ni
ni
n
1
2
3
4
5
6
60
65
70
75
100
120
3
3
7
5
8
4
3 3 7 5
30 30 30 30
8
30
4
30

26.

60, 60, 60, 65, 65, 65, 70, 70, 70, 70, 70, 70, 70, 75, 75, 75, 75, 75,
100, 100, 100, 100, 100, 100, 100, 100, 120, 120, 120, 120
Mo 100
60, 60, 60, 65, 65, 65, 70, 70, 70, 70, 70, 70, 70, 75, 75, 75, 75, 75,
100, 100, 100, 100, 100, 100, 100, 100, 120, 120, 120, 120
75 75
Me
75
2
R xmax xmin
R 120 60 60

27.

Номер группы
i
1
2
3
4
5
6
Число обращений
xi
60
65
70
75
100
120
3
3
7
5
8
4
Частота
ni
x1n1 x2 n2 xm nm 1 m
xВ
xi ni
n
n i 1
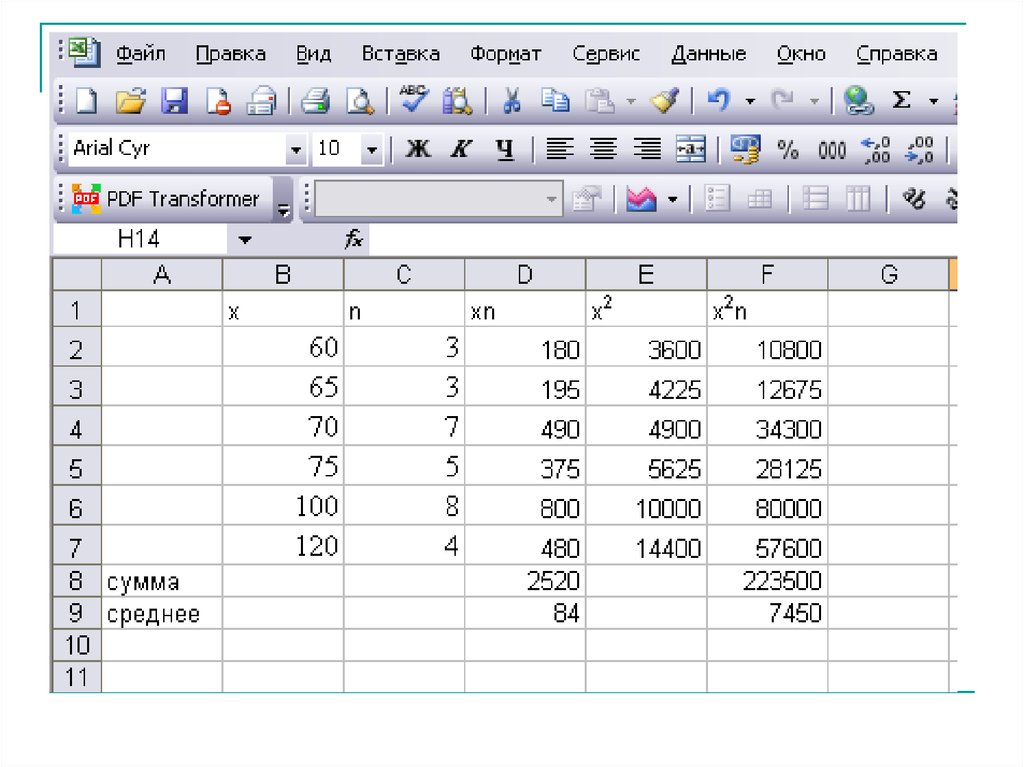
60 3 65 3 70 7 75 5 100 8 120 4
xВ
84
30

28.

29.

30.

Номер группы
i
Число обращений
xi
1 2 3 4 5
6
60 65 70 75 100 120
ni
3
Частота
3
7
5
8
4
1 m
2
DВ xi xВ ni
n i 1
1
2
2
2
60 84 3 65 84 3 70 84 7
DВ
30
2
2
2
75 84 5 100 84 8 120 84 4 394

31.

32.

33.

1
1
2
DB xi ni xi ni
n i 1
n i 1
m
m
2

34.

35.

1
1
2
DB xi ni xi ni
n i 1
n i 1
m
m
2
DB 7450 842 394
n
30
s
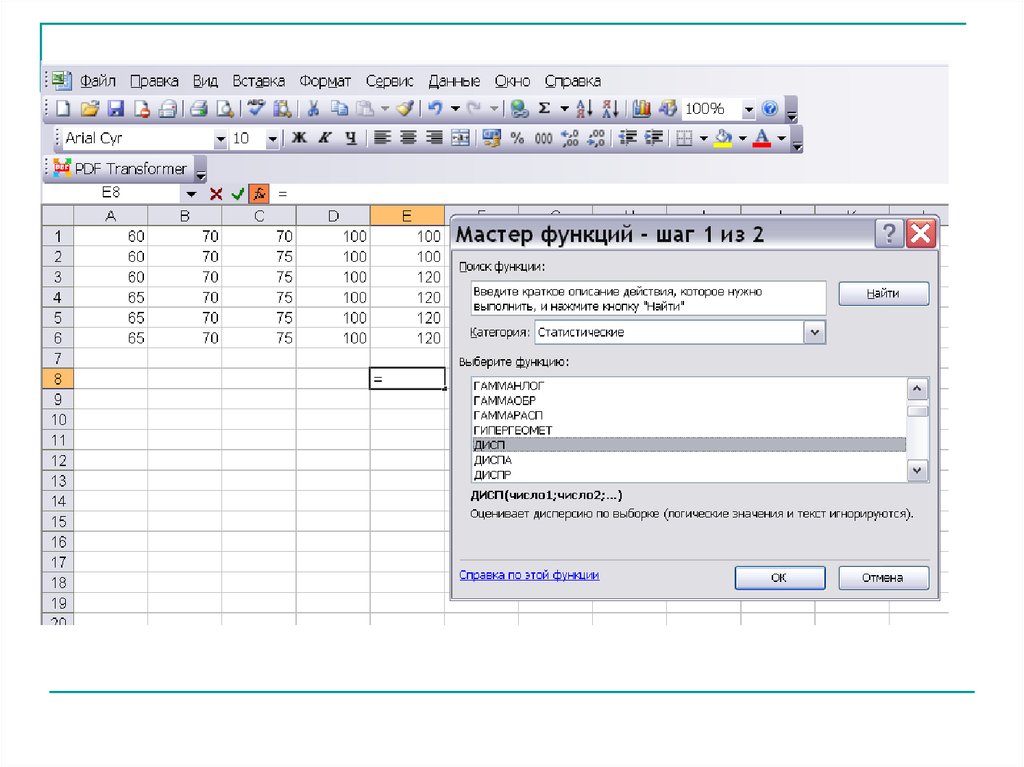
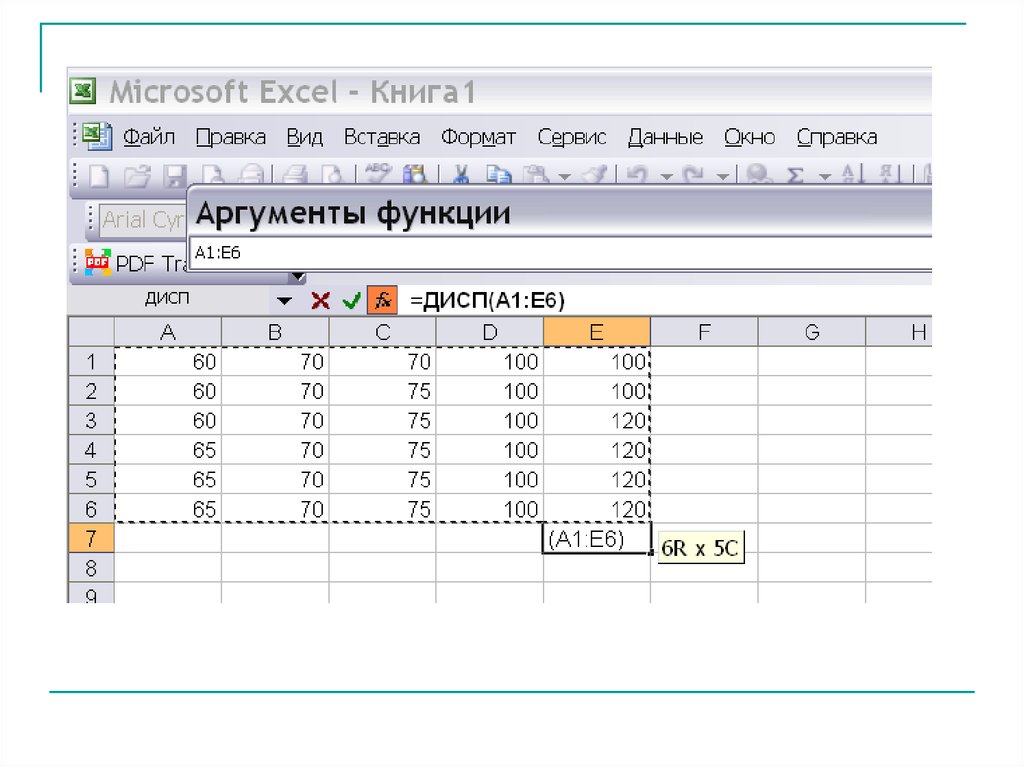
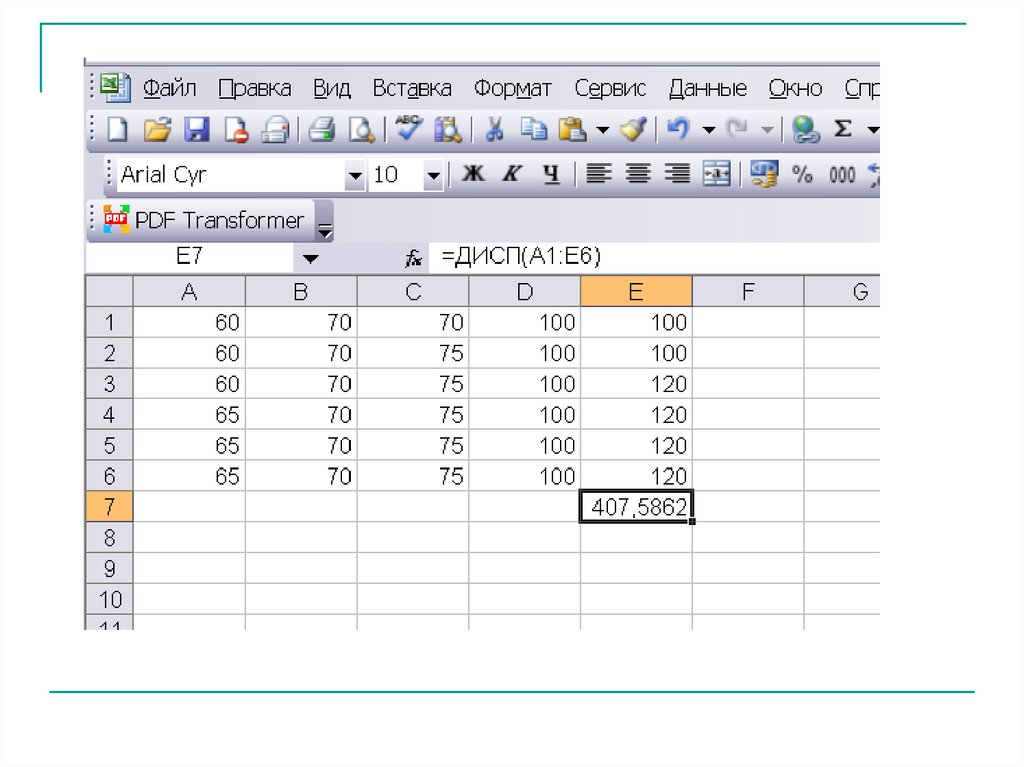
DВ
394 407,59
n 1
29
2

36.

37.

38.

39.

Составить эмпирическую функцию распределения
x
x 60
60 x 65
65 x 70
70 x 75
75 x 100
100 x 120
x 120
F*(x)
0
3
30
3
3
6
30 30 30
3
3
7 13
30 30 30 30
3
3
7
5 18
30 30 30 30 30
3
3
7
5
8 26
30 30 30 30 30 30
3
3
7
5
8
4
1
30 30 30 30 30 30

40.

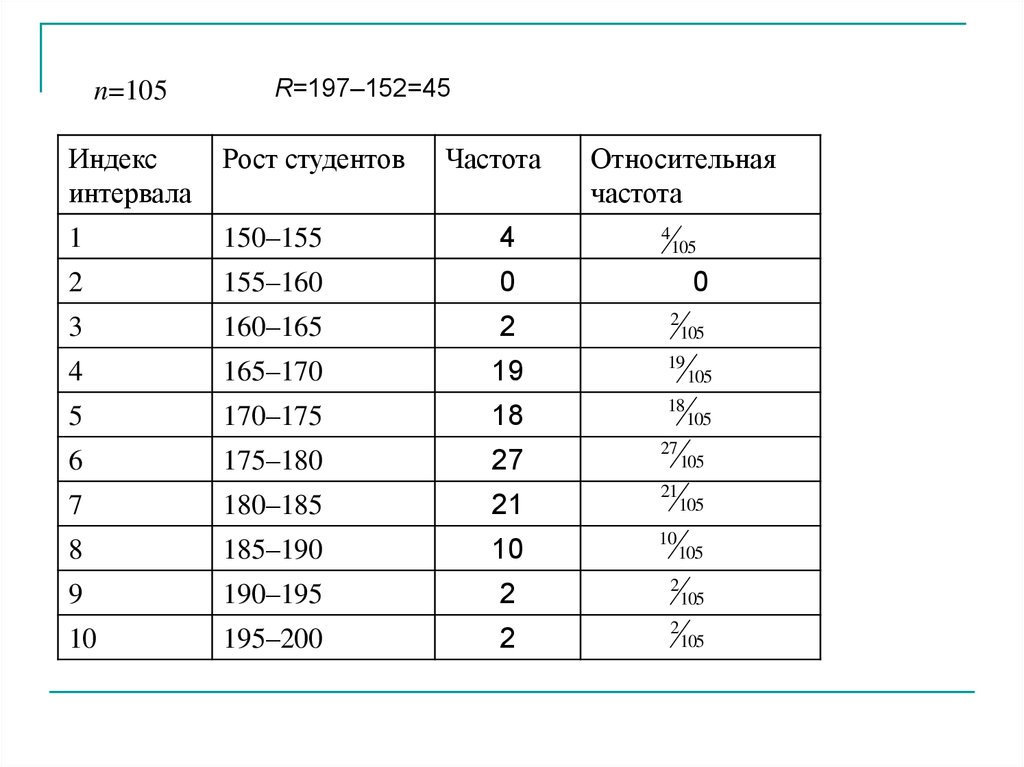
В таблице приведена выборка результатов измерения роста 105
студентов. Измерения проводились с точностью до 1 см. Требуется
составить интервальный вариационный ряд
155
170
185
180
188
152
173
178
178
168
185
173
170
183
175
173
170
183
175
180
175
193
178
183
180
197
178
181
187
168
174
179
184
183
178
180
178
163
166
178
175
182
190
167
170
178
183
170
178
181
173
168
185
175
170
155
169
186
179
189
155
174
179
179
169
186
174
171
184
175
193
178
184
180
196
175
181
188
168
179
178
183
184
178
181
177
163
166
178
175
183
190
167
170
178
183
170
178
182
173
168
186
176
171
188

41.

n=105
R=197–152=45
Индекс
интервала
Рост студентов
Частота
Относительная
частота
1
150–155
4
2
155–160
0
3
160–165
2
2
4
165–170
19
19
5
170–175
18
18
6
175–180
27
7
180–185
21
8
185–190
10
9
190–195
2
2
10
195–200
2
2
4
105
0
27
105
105
105
105
21
105
10
105
105
105

42. Интервальные оценки

В каждом рассмотренном примере результат зависит от рассмотренных
выборок. Вполне возможно, что для других выборок будет получен
другой результат.
Возникает вопрос: на сколько статистические характеристики
отличаются от соответствующих генеральных характеристик?
Для ответа на этот вопрос вводится понятие интервальных оценок
генеральных характеристик
Интервальной называют оценку, которая определяется двумя числами
– концами интервала
Пусть Θ* - оценка неизвестного параметра Θ, полученная по данным
выборки. Оценка тем точнее, чем меньше величина |Θ
- Θ*|
Если δ > 0 и |Θ - Θ*| < δ, то чем меньше δ, тем точнее оценка Θ*, т.е.
число δ характеризует точность оценки

43.

Доверительной вероятностью (надежностью) оценки Θ*
параметра Θ называется вероятность γ, с которой осуществляется
неравенство
|Θ - Θ*| < δ, т.е.
P *
Обычно доверительная вероятность задается заранее, причем в
качестве γ берут число, близкое к единице.
Наиболее часто надежность задается равной 0,95; 0,99; 0,999.

44.

- Θ*| < δ равносильно неравенству
-δ < Θ - Θ* < δ, или Θ* - δ < Θ < Θ* + δ, то формулу вероятности
Так как неравенство |Θ
можно записать в виде
P * *
Вероятность того, что интервал (Θ*
- δ, Θ* + δ) заключает в себе
неизвестный параметр Θ, равна γ.
- δ, Θ* + δ), который покрывает неизвестный параметр
Θ с заданной надежностью γ, называется доверительным
Интервал (Θ*
интервалом.
Концы доверительного интервала называются доверительными
границами.