Similar presentations:
Математическая статистика
1. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
2. Математическая статистика -
Математическая статистика этораздел
математики,
посвящённый
математическим методам сбора, систематизации,
обработки,
анализа
и
использования
экспериментальных данных.
3.
Вариационные ряды иих характеристики
4.
Пусть требуется изучить некоторую совокупностьобъектов относительно некоторого количественного
или качественного признака.
Иногда проводят сплошное обследование.
На практике чаще всего делают выборку, т.е.
отбирают часть объектов совокупности.
5.
x1, xn
i
2
, ... , x
n
n.
ni
wi
n
n
нак
i 1
n
нак
i
n i 1 ,
нак
1
n
n1
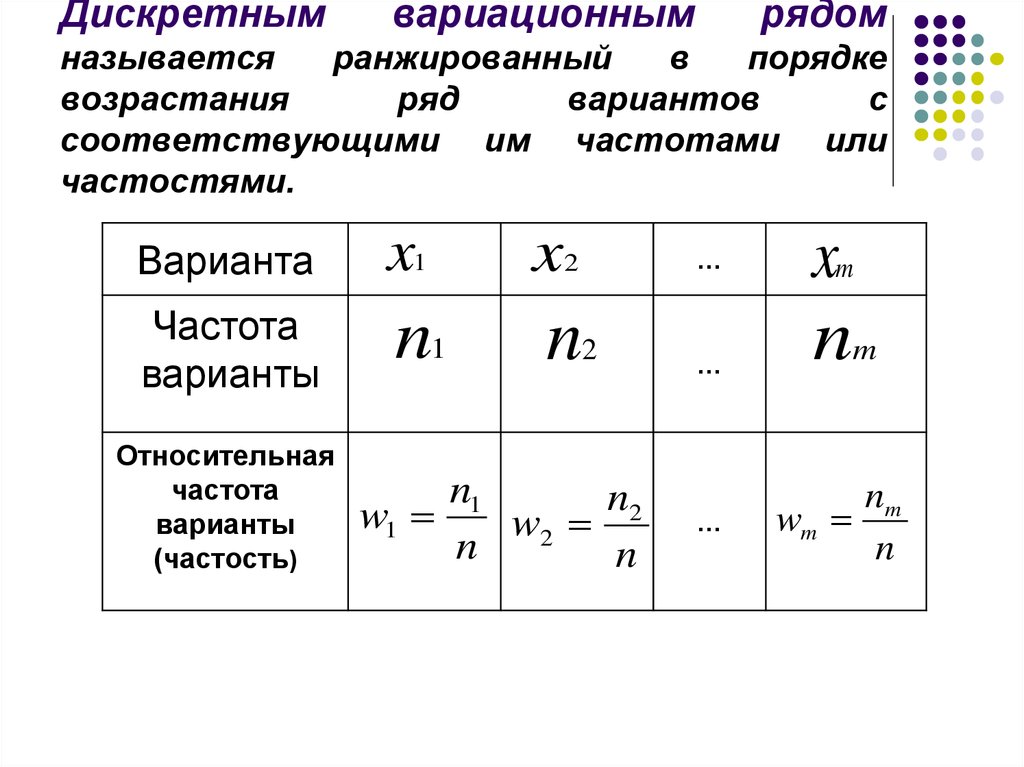
6. Дискретным вариационным рядом называется ранжированный в порядке возрастания ряд вариантов с соответствующими им частотами или
частостями.Варианта
x1
x2
Частота
варианты
n1
n2
Относительная
частота
варианты
(частость)
n1
n2
w1
w2
n
n
…
…
…
xm
nm
nm
wm
n
7.
Пример. 20 студентов на экзамене попсихологии получили такие оценки (по
пятибалльной системе): 5, 4, 4, 3, 3, 5, 2, 3,
4, 3, 3, 4, 4, 4, 3, 5, 4, 4, 3 ,5. Составить
дискретный вариационный ряд.
8. Дискретный вариационный ряд:
Варианта2
3
4
5
Частота
варианты
1
7
8
4
9.
Пример. Имеются данные о заработнойплате сотрудников предприятия за сентябрь
2012 г., тыс. руб.:
10,11, 21,13,14,15,14,15,15,19,15,15,16,16,
16,19,16,16,19,19,19,16,19,17,17,17,18,18,18,
18,18,18,18,18,19,15,19,20,21,20,21,21,20,12,
23,23, 12,22, 12,21,21,21, 17,17,17
10 11 12 13 14 15 16
17
18
19
20
21
22
23
Ито
го
1
1
3
1
55
1
2
5
6
55
10.
1 3,322 lg nЕсли число различных значений признака в выборке
велико, или признак является непрерывным (т.е.
может принять любое значение в некотором
интервале),
то
составляют
интервальный
вариационный ряд: нужно весь промежуток
изменения значений выборки (от минимального до
максимального) разбить на интервалы, а затем
подсчитать число значений из выборки, попадающих
в каждый интервал (частоты).
При этом оптимальное количество интервалов
определяется по формуле
k 1 3,322 lg n
а длина интервала
h
Х max X min
1 3,322 lg n
11. Интервальный вариационный ряд
[ x1 ; x 2 ) [ x ; x )2
n1
n1
w1
n
3
…
n2
…
n2
w2
n
…
[ xm ; xm 1]
nm
nm
wm
n
12.
hk 1 3,322 lg 55 6,8
23 10
6,8
2
Границы
интервала,
хi-xi+1
[10,12)
[12,14)
[14,16)
[16,18)
[18,20)
[20,22)
[22,24)
Середина
интервала
11
13
15
17
19
21
23
2
4
8
12
16
10
3
2
6
14
26
42
52
55
Частота,
ni
xi *
niнак
Накопленная
частота,
13. Графическое изображение вариационных рядов
14.
Полигоном частот (относительныхчастот)
интервального
ряда
называется ломаная с вершинами в
точках ( x , n ), i 1, k
(в точках ( x ,W ) ) ( х середины интервалов).
*
i
i
*
i
i
*
i
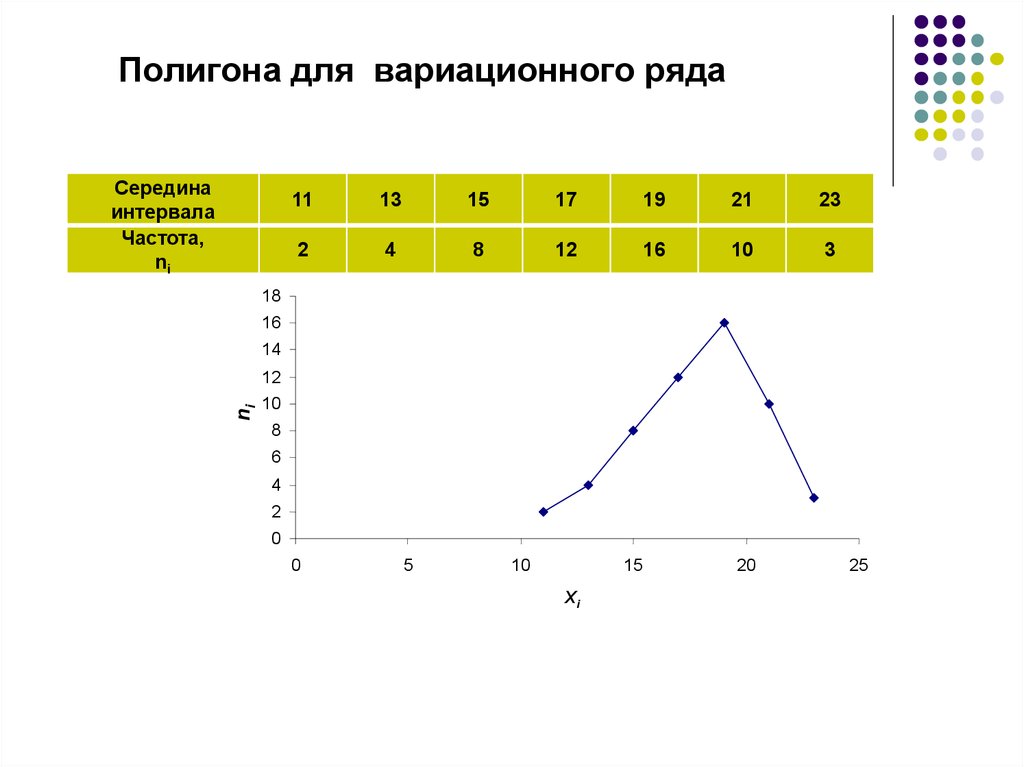
15. Полигона для вариационного ряда
Серединаинтервала
Частота,
ni
11
13
15
17
19
21
23
2
4
8
12
16
10
3
18
16
14
ni
12
10
8
6
4
2
0
0
5
10
15
Xi
20
25
16. Гистограмма
Применяется для изображения толькоинтервальных вариационных рядов и
представляет собой ступенчатую фигуру из
прямоугольников с основаниями, равными
интервалам значений признака и высотами,
равными частотам (частостям) интервалов.
При этом по оси абсцисс откладываются
интервалы, а по оси ординат – частоты (или
частости) в случае равенства интервалов,
или плотности распределения частот (или
частостей) в случае неравенства интервалов.
17. Гистограмма
Границыинтервала,
хi-xi+1
[10,12)
[12,14)
[14,16)
[16,18)
[18,20)
[20,22)
[22,24)
Частота,
ni
2
4
8
12
16
10
3
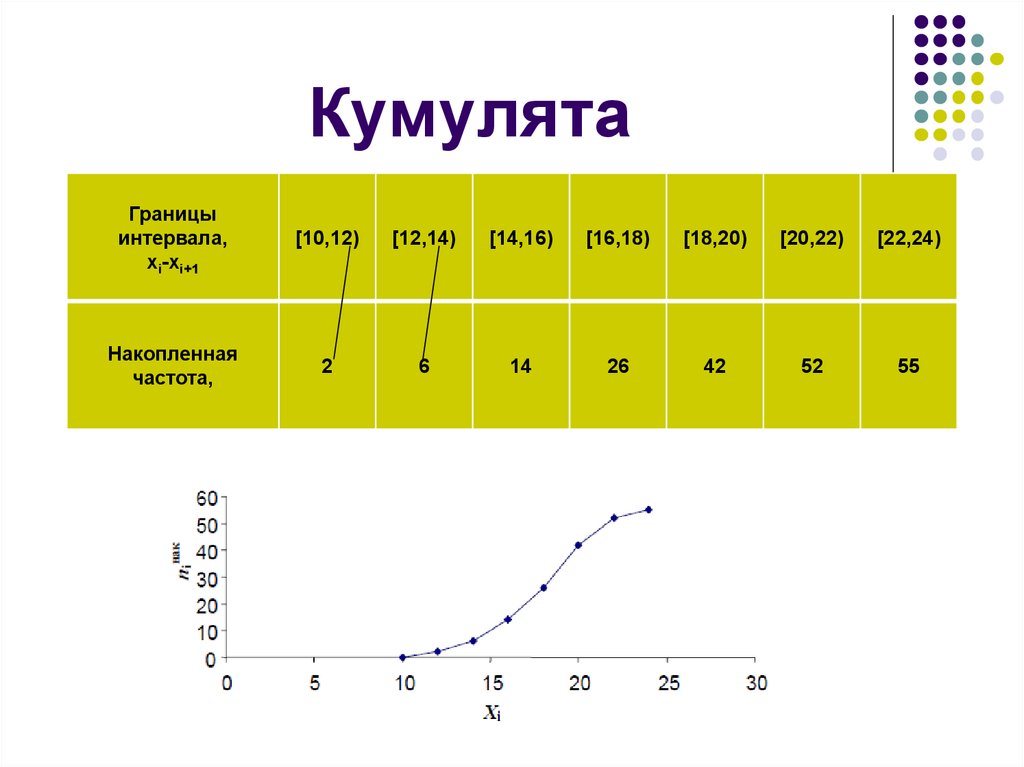
18. Кумулята
Кумулятивная кривая (кумулята) –кривая накопленных частот.
Представляет ломаную, соединяющую точки
( хi ; пiнак )
Для интервального вариационного ряда
ломаная начинается с точки ( x нач ; 0 ) .
19. Кумулята
Границыинтервала,
хi-xi+1
[10,12)
[12,14)
[14,16)
[16,18)
[18,20)
[20,22)
[22,24)
Накопленная
частота,
2
6
14
26
42
52
55
20. Числовые характеристики вариационного ряда:
Средние величины• Показатели вариации
21. Средние величины
Средние величины характеризуют значениепризнака, вокруг которого концентрируются
наблюдения или, как говорят, центральную
тенденцию распределения.
К ним относят:
среднюю арифметическую,
Моду,
медиану.
22.
Среднейарифметической
вариационного
ряда
называется сумма произведений всех вариантов на
соответствующие частоты, деленная на сумму частот:
m
х
x n
i 1
i
n
i
,
где xi
- варианты дискретного ряда или середины
интервалов интервального вариационного ряда;
ni - соответствующие им частоты.
23.
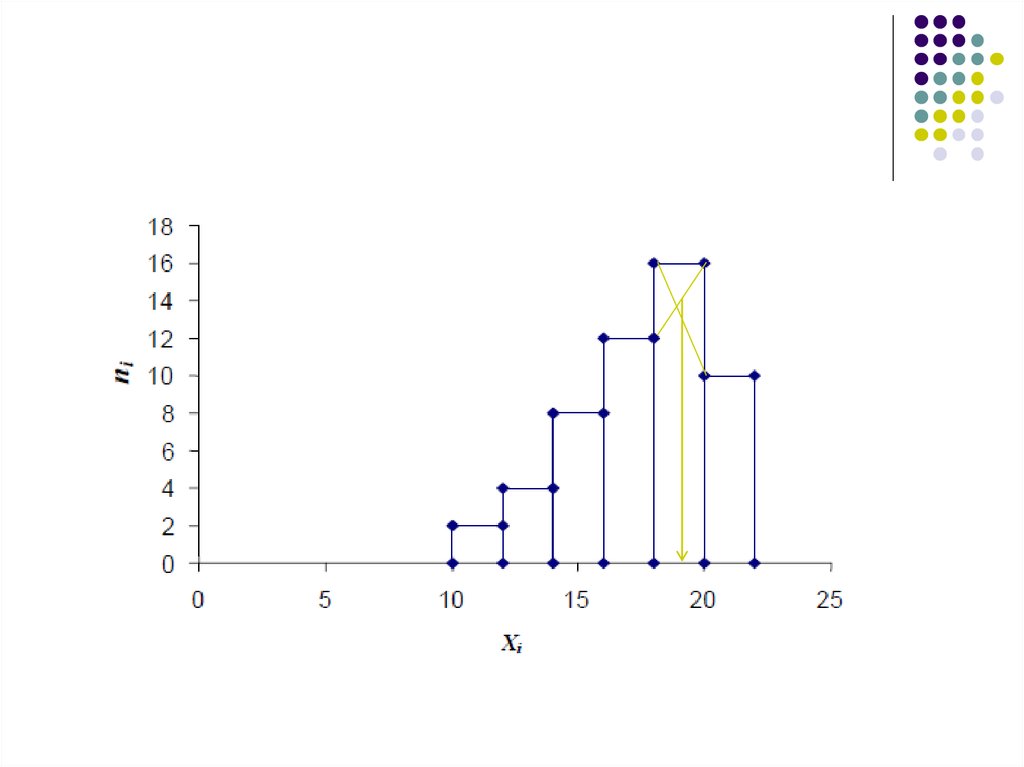
Мода(Mo) - это значение, которое
встречается в выборке наиболее часто.
Мода может быть приближённа найдена по
гистограмме: выбираем самую высокую
ступеньку, её вершины крест-накрест
соединяем с вершинами предшествующей
и следующей за ней степеньками, из точки
пересечения опускаем перпендикуляд на
ось ОХ, это и есть мода.
24.
25. Моду можно найти по формуле
26.
МедианаMe - это значение, которое
делит вариационный ряд пополам.
Медиана может быть приближенно найдена
с помощью кумуляты как значение признака,
для которого нак п
пх
2
27. Медиану можно найти по формуле
28. Показатели вариации
Дисперсиейвариационного
ряда
называется средняя арифметическая
квадратов отклонений вариантов от их
средней арифметической:
x
m
D
i 1
i
x
2
ni
n
Среднее квадратическое отклонение
D






























 mathematics
mathematics








