1_Obzor_osnovnykh_ponyatiy_MS_STS

1. Обзор. Основные понятия математической статистики

1

2. Основные понятия математической статистики

Генеральной совокупностью Х называется вся подлежащая
изучению совокупность объектов (наблюдений)
Отдельное значение признака Х называется вариантой
Выборочной совокупностью (выборкой) называют
множество результатов наблюдений, случайно отобранных
из генеральной совокупности.
Число вариант есть объем генеральной или выборочной
совокупности (N или n)
Объем генеральной совокупности может быть и
бесконечным
2

3. Дискретный вариационный ряд

Пусть из генеральной совокупности извлечена выборка, причем х1 наблюдается m1
k
раз, х2 – m2 раз, …, хк – mк раз, и mk n, где п – объем выборки.
i 1
Определение: Перечень ранжированных
дискретным вариационным рядом
Дискретный вариационный ряд:
x1
x2
X
m2
m1
mi
w2
w1
wi
вариант и их частот называется
….
…
…
xk
mk
wk
n
1
k
mi
- относительные частоты или частости, wi 1 .
хi.- варианты; mi – частоты; wi
n
i 1
нак
Накопленная частота в точке x ( mx )- показывает сколько наблюдалось вариант
меньших x
нак
x
Накопленная частость w
mхнак
n
3

4. Интервальный вариационный ряд

Этапы построения интервальных рядов:
1. Находятся наибольшее и наименьшее значение признака xmin и xmax .
2. Определяется количество интервалов k 1 3.32 lg n и длина интервала
h ( xmax xmin ) / k
3. За начало первого интервала рекомендуется брать величину õíà÷ xmin
4. xmax принадлежит последнему интервалу.
Интервальный вариационный ряд:
Интервал
Частоты
Частости
x0 x1
x1 x2
m1
w1
m2
w2
….
…
…
xk 1 xk
mk
wk
n
1
Интервальный ряд может быть условно перестроен в дискретный ряд путем замены
каждого интервала его серединой
4

5. Графическое изображение вариационных рядов - полигон частот (служит для изображения дискретного вариационного ряда): ломаная,

отрезки которой соединяют точки с координатами (x1, m1), (x2,m2),…,
(xk, mk), где xi откладываются на оси абсцисс, а mi – на оси ординат. Если на оси
ординат откладывать относительные (wi) частоты, то получим полигон
относительных частот;
-гистограмма (служит для изображения интервальных вариационных рядов), представляет собой ступенчатую фигуру, состоящую из прямоугольников,
основаниями которых служат интервалы длиной h, а высотами – частоты
(гистограмма частот) или частости (гистограмма относительных частот);
-кумулятивная кривая (кумулята) – кривая накопленных частот (частостей).
5

6. Эмпирическая функция распределения

Эмпирической функцией распределения Fn (x) называется относительная
частота того, что признак Х примет значение, меньше заданного х, то есть:
Fn ( x) w( X x) wxíàê
при x x1 ;
0,
w ,
при x1 x x2 ;
1
при x2 x x3 ;
Fn ( x) w1 w2 ,
...
....... .....
w1 w2 ... wk при x xk
Функция Fn (x) является «ступенчатой», имеются разрывы в точках, которым
соответствуют наблюдаемые значения вариант. Величина скачка равна
относительной частоте варианты.
6

7. Числовые характеристики выборочной совокупности

1 Характеристики положения
- выборочная средняя - это среднее арифметическое значение признака
выборочной совокупности:
XВ
х1 х2 ... хп
простая (невзвешенная ) средняя,
п
k
x i mi
m1 x1 m 2 x 2 ... m k x k
i 1
XÂ
взвешенная средняя,
n
n
где xi – варианты дискретного ряда или середины интервалов
интервального вариационного ряда,
mi – соответствующие частоты,
k – число интервалов.
~
- медиана дискретного вариационного ряда М е - значение признака,
приходящееся на середину ранжированного ряда наблюдений.
~
- мода М о - варианта, которая имеет наибольшую частоту.

8. Числовые характеристики выборочной совокупности

2 Характеристики вариации
- размах вариации: R= xmax - xmin
- среднее линейное отклонение вариационного ряда:
k
x X m
d
i 1
i
i
n
- выборочная дисперсия:
n
(x X )
2
i
S 2 i 1
, - простая дисперсия
n
k
(x X ) m
2
S
2
i 1
Легко доказать: S 2
i
i
n
- для сгруппированных данных
1 k 2
xi mi ( X ) 2
n i 1
- выборочное среднее квадратическое отклонение: S S 2 .
- коэффициент вариации: KV~
S
100%
X

9. Числовые характеристики выборочной совокупности

3 Характеристики форм
- коэффициент асимметрии вариационного ряда:
k
~
À
~
S
3
3
(x X ) m
3
i
i 1
i
nS 3
- эксцесс вариационного ряда:
k
~
Å
~
S
(x X ) m
4
4
4
3
i
i 1
i
nS 4
3
Моменты случайных величин
- начальный момент l -ого порядка
mx
~l i i .
n
l
- центральный момент l -ого порядка:
( x X ) mi
~l i
n
l

10. Точечные оценки и требования к ним

Точечной оценкой называют некоторую вектор – функцию
результатов наблюдения ˆ ( x ,..., x ) , значения компонент которой
1
n
принимают за наилучшее приближение, в данных условиях, к
значениям компонент вектора
параметров генеральной
совокупности.
Свойства оценок
1. Оценка ˆ параметра называется состоятельной, если она
удовлетворяет закону больших чисел, т. е. сходится по вероятности
к оцениваемому параметру:
P
ˆ
ˆ
lim P 1 или
2. Оценка ˆ параметра называется несмещенной, если ее
математическое ожидание равно оцениваемому параметру, т. е. если
выполняется равенство
M ( ˆ) .
Если данное равенство не выполняется, то оценку будут
называть смещенной.
3. Несмещенная оценка ˆ
параметра называется
эффективной, если она имеет наименьшую дисперсию среди всех
возможных несмещенных оценок параметра θ, вычисленных по
выборкам одного и того же объема n.
D( ˆ ) min .
íåñì
10

11. Проверка статистических гипотез

12. Основные понятия

Слайд №1
Основные понятия
Определение: Статистической гипотезой называется любое
предположение о виде или параметрах неизвестного закона распределения
генеральной совокупности.
Определение: Подлежащую проверке гипотезу
основной или нулевой и обозначать Н0.
Гипотезы разделяют на простые и сложные.
будем
называть
Определение: Гипотеза называется простой, если она однозначно
характеризует параметр или свойство генеральной совокупности (Н0: генеральная совокупность распределена по нормальному закону). В
противном случае гипотеза называется сложной.
Определение: Конкурирующей (альтернативной) гипотезой (Н1) будем
называть гипотезу противоположную нулевой.
Определение: Статистическим критерием называют однозначно
определенное правило, устанавливающее условия, при которых
проверяемую гипотезу (Н0) следует либо отвергнуть, либо принять.

13.

Продолжение слайда №1
Пусть из генеральной совокупности извлечена выборка объемом n и вычислена
статистика n* ( x1 ,..., xn ) , точное или приближенное распределение которой известно.
Затем по этому выборочному распределению определяется критическое значение
кр , которое все множество возможных значений статистики n* будет разбивать на
два непересекающихся подмножества (области): критическую область 0 (область
отклонения гипотезы) и область принятия решений 1 (гипотезы).
Точки, разделяющие критическую область и область принятия решения,
называются критическими.
- Если, полученное по данным выборки, значение статистики критерия попадает
в критическую область n* 0 , то гипотеза Н0 отвергается.
- Если наблюденное значение статистики критерия не попадает в критическую
область n* 0 , то гипотеза Н0 не отклоняется.

14.

Продолжение слайда №1
Рассмотрим ситуации:
- гипотеза Н0 верна и ее не отвергают согласно критерию;
- гипотеза Н0 не верна и ее отвергают согласно критерию;
- гипотеза Н0 верна, но ее отвергают согласно критерию (говорят об ошибке
первого рода);
- гипотеза Н0 не верна, но ее принимают согласно критерию (говорят об
ошибке второго рода).
Определение: Уровнем значимости 1 называют вероятность совершить
ошибку первого рода
Определение:
Мощностью статистического критерия будем называть
вероятность того, что нулевая гипотеза (Н0) будет отвергнута, если верна
конкурирующая гипотеза (Н1), то есть вероятность P 1 не совершить ошибку
второго рода.
Пусть P( / H ) - вероятность попадания статистики критерия в критическую
область, если верна гипотеза Н0 - вероятность совершить ошибку первого рода, а
P( / H ) - вероятность не совершить ошибку второго рода, тогда естественно
требовать:
*
n
*
n
0
0
0
1
*
P( n 0 / H 0 )
*
P( n 0 / H1 ) 1 max

15. Общая схема проверки статистической гипотезы

Слайд №2
В зависимости от содержания конкурирующей гипотезы Н1 выбирают
правостороннюю, левостороннюю или двустороннюю
критические области.
Критические точки kp (точки, разделяющие критическую область и область
принятия решения) при заданном уровне значимости "α" находят из уравнений:
- для правосторонней критической области:
P( n* kp )
Рисунок 1 - График плотности распределения статистики n* , выделения правосторонней
критической области (II) и области принятия решения(I)
- для левосторонней критической области:
P( n* kp )
Рисунок 2 - График плотности распределения статистики n* , выделения левосторонней
критической области (II) и области принятия решения (I)

16.

Продолжение слайда №2
- для двусторонней критической области
P( n* kp2 ) , P( n* kp1 ) , где kp1 kp2
2
2
Рисунок 3 - График плотности распределения статистики n* и областей: критической – II,
принятия решения -I
Определив в каждом случае границы критической области, проверяем гипотезу Н0 ,
предварительно вычислив по выборочным данным :
- для правосторонней критической области: если n* kp , то гипотеза
n
Н0 отвергается;
- для левосторонней критической области: если
n* kp ,
то гипотеза Н0
отвергается;
- для двусторонней критической области: если êð 2 n* kp1, то гипотеза Н0
отвергается.

17.

Продолжение слайда №4
Пример: На основании сделанного прогноза средняя дебиторская
задолженность однотипных предприятий региона должна составить α0 =120
ден, ед. выборочная проверка 10 предприятий установила, что средняя
задолженность х =135 ден.ед. s= 20 ден.ед.
На уровне значимости =0,05 выяснить можно ли принять данный прогноз.
Решение:
Для проверки нулевой гипотезы Н0: α0=120
при альтернативной
Н1: α1=135 построим статистику
t
X a0
135 120
n 1
10 1 2,25 ,
S
20
1 0 строим правостороннюю критическую область
t kp (2 , n 1) St 1 (2 , n 1)
tkp (2 0,05, n 1) tkp (0,1;9) 1,83
Н0 отвергаем, т.е на 5% уровне значимости сделанный
прогноз должен быть отвергнут.
tнабл tkp

18. Классификация методов исследования взаимосвязи компонент многомерного случайного вектора признаков

Тип случайных величин
Количественные
Порядковые
Номинальные
Многомерный
корреляционный
анализ
Методы
ранговой
корреляции
Анализ
таблиц
сопряженности
Методы исследования взаимосязи

19. Многомерный корреляционный анализ

Корреляционный анализ – это совокупность
методов оценки корреляционных характеристик и
проверки статистических гипотез о них по
выборочным данным, извлеченным из генеральной
совокупности, распределенной по многомерному
нормальному закону с плотностью распределения
вида:
f ( x)
1
( 2 ) n / 2
1
exp ( x a ) T 1 ( x a ) .
2

20. ОСНОВНЫЕ ВИДЫ ЗАВИСИМОСТЕЙ

Слайд № 1
ОСНОВНЫЕ ВИДЫ ЗАВИСИМОСТЕЙ
Главной задачей корреляционного анализа является оценка
взаимосвязей между переменными величинами на основе выборочных
данных.
Различают два вида зависимостей:
Функциональная зависимость – зависимость, при которой каждому
значению одной переменной соответствует определенное значение другой.
Стохастическая (вероятностная, статистическая) – зависимость,
когда каждому значению одной переменной соответствует условное
распределение другой.
Частным случаем статистической зависимости является корреляционная
зависимость.
Корреляционная зависимость между двумя переменными величинами
называется функциональная зависимость между условным математическим
ожиданием одной из них и возможными значениями другой.

21. КОРРЕЛЯЦИОННОЕ ПОЛЕ

Слайд № 8
КОРРЕЛЯЦИОННОЕ ПОЛЕ

22. Постановка задачи

Рассмотрим
случайный
вектор
количественных
признаков X ( X 1 , X 2 ,..., X n ) T . Ставится задача на основе
выборочных данных объемом N, извлеченных из n-мерной
нормально распределенной генеральной совокупности и
представленных в виде матрицы типа «объект-свойство»,
исследовать взаимосвязи между компонентами случайного
вектора X.
Матрица исходных данных имеет вид:
x11 x12 x1n
x 21 x 22 x 2 n
,
X
x N 1 x N 2 x Nn
где xij – наблюдаемое значение j-го признака на i-ом объекте
выборочной совокупности.

23. Классификация основных корреляционных характеристик

Корреляционные характеристики
парной связи
Ковариация
Частный
коэффициент
корреляции
Парный
коэффициент
корреляции
множественной связи
Коэффициент
детерминации
Множественный
коэффициент
корреляции

24. Парный коэффициент корреляции

Определение парного коэффициента корреляции между
признаками X j и X k :
( X j MX j ) ( X MX )
jk
k
k
X j X k jk M
,
Xj
Xk
Xj
Xk
где jk – ковариация случайных величин X j и X k ;
X j и X k – средние квадратические отклонения признаков X j и X k
соответственно.
Оценка парного коэффициента корреляции между признаками X j и X k :
S jk
1 N ( xij X j ) ( xik X k )
rX j X k r jk
,
N i 1
Sj
Sk
S j S k
где X j и X k – средние арифметические значения признаков X j и X k
соответственно;
S j и S k – выборочные средние квадратические отклонения признаков X j и
X k соответственно;
S jk – оценка ковариации признаков X j и X k .

25. Матрица парных коэффициентов корреляции

Матрица парных коэффициентов корреляции:
12 1n
1
1 2n
21
.
R
n1 n 2 1
Оценка матрицы парных коэффициентов корреляции:
1 r12 r1n
r21 1 r2 n
ˆ
.
R
r
r
1
n1 n 2

26. Свойства парного коэффициента корреляции

1) парный коэффициент корреляции принимает значения от -1
до +1;
2) если парный коэффициент корреляции между признаками
X j и X k равен нулю, то признаки X j и X k являются
некоррелированными;
3) парный коэффициент корреляции между признаками X j и
X k по модулю равен единице, тогда и только тогда, когда
признаки X j и X k связаны линейной функциональной
зависимостью;
4) положительное
значение
парного
коэффициента
корреляции между признаками X j и X k указывает на
прямую линейную связь, отрицательное значение – на
обратную линейную связь признаков.

27. Частный коэффициент корреляции

Коэффициент корреляции между признаками X j и
X k , «очищенный» от влияния остальных (n-2)
X1, X 2 ,..., X j 1 , X j 1,..., X k 1, X k 1,..., X n ,
признаков
называется частным коэффициентом корреляции.

28.

Определение частного коэффициента корреляции между
признаками X j и X k при устранении влияния всех остальных
признаков:
Rij
ij /(...)
,
Rii R jj
где Rsm – алгебраическое дополнение элемента sm матрицы парных
коэффициентов корреляции.
Оценка частного коэффициента корреляции между признаками X j
и X k при устранении влияния всех остальных признаков:
Rˆ ij
rij /(...)
,
Rˆ ii Rˆ jj
где R̂sm – алгебраическое дополнение элемента rsm выборочной
матрицы парных коэффициентов корреляции.

29. Коэффициент детерминации

Определение коэффициента детерминации между
признаком X j и остальными (n-1) компонентами вектора
Х:
R
2
X j /(...) 1
.
R jj
Оценка коэффициента детерминации между признаком X j
и остальными (n-1) компонентами вектора Х:
ˆ
R
R X2 j /(...) 1
.
ˆ
R jj

30. Множественный коэффициент корреляции

Определение множественного коэффициента
корреляции между признаком X j и остальными
(n-1) компонентами вектора Х:
Xj /(...) X2 j /(...) .
Оценка множественного коэффициента
корреляции между признаком X j и остальными
(n-1) компонентами вектора Х:
R Xj /(...) R X2 j /(...) .

31.

Свойства коэффициента детерминации
1)
2)
3)
коэффициент детерминации принимает значения
от 0 до 1;
если коэффициент детерминации между признаком
X j и всеми остальными признаками равен нулю,
то признак X j не коррелирован с признаками
X 1 , X 2 ,..., X j 1 , X j 1 ,..., X n ;
если коэффициент детерминации между признаком
X j и всеми остальными признаками равен
единице, то между признаком X j и признаками
X 1 , X 2 ,..., X j 1 , X j 1 ,..., X n существует линейная
функциональная зависимость.

32.

Проверка значимости парных
коэффициентов корреляции
H 0 : jk 0 (парный коэффициент корреляции между
признаками X j и X k незначим);
H 1 : jk 0 (парный коэффициент корреляции между
признаками X j и X k значим).
Для
проверки
статистика
нулевой гипотезы используется
r jk
t
N 2,
имеющая
при
1 r jk2
справедливости
гипотезы
H0
распределение
Стьюдента с числом степеней свободы N-2.

33.

Проверка значимости частных
коэффициентов корреляции
H 0 : jk /(...) 0 (частный коэффициент корреляции между
признаками X j и X k при устранении влияния
всех остальных признаков незначим);
H 1 : jk /(...) 0 (частный коэффициент корреляции между
признаками X j и X k при устранении влияния
всех остальных признаков значим).
Для проверки нулевой гипотезы используется статистика
r jk /(...)
t
N n , имеющая при справедливости
1 r jk2 /(...)
гипотезы H 0 распределение Стьюдента с числом степеней
свободы N-n-2.

34. Доверительные интервалы для значимо отличных от нуля характеристик линейной зависимости

Если частный коэффициент корреляции ij /(...) значимо отличен от нуля и
имеет выборочную оценку rij /(...) , то для построения доверительного интервала
осуществим над rij /(...) Z – преобразование Фишера
Zr
1 1 rij /(...)
ln
2 1 rij /(...)
1 1
1
).
Статистика Z r N ( ln
,
2 1 n l 3
Следовательно, статистика t
Из уравнения
интервал для Z
Zr Z
1/(n l 3)
N (0,1) .
P( t ) , находим Ф 1 ( )
2
Zr
n l 3
Z Zr
и доверительный
n l 3
zmin z zmax
Осуществив преобразование обратное Z – преобразованию Фишера
получим доверительный интервал для ij /(...)
rmin rmax .

35.

Проверка значимости коэффициентов
детерминации
H 0 : 2j /(...) 0 (признаки X 1 , X 2 ,..., X j 1 , X j 1 ,..., X n не
оказывают значимого влияния на признак X j );
H 1 : 2j /(...) 0 (признаки X 1 , X 2 ,..., X j 1 , X j 1 ,..., X n оказывают
значимое влияние на признак X j ).
Для проверки нулевой гипотезы используется статистика
R 2j /(...) /( n 1)
, имеющая при справедливости гипотезы
F
2
1 R j /(...) /( N n)
H 0 распределение Фишера с числом степеней свободы n-1 и
N-n.

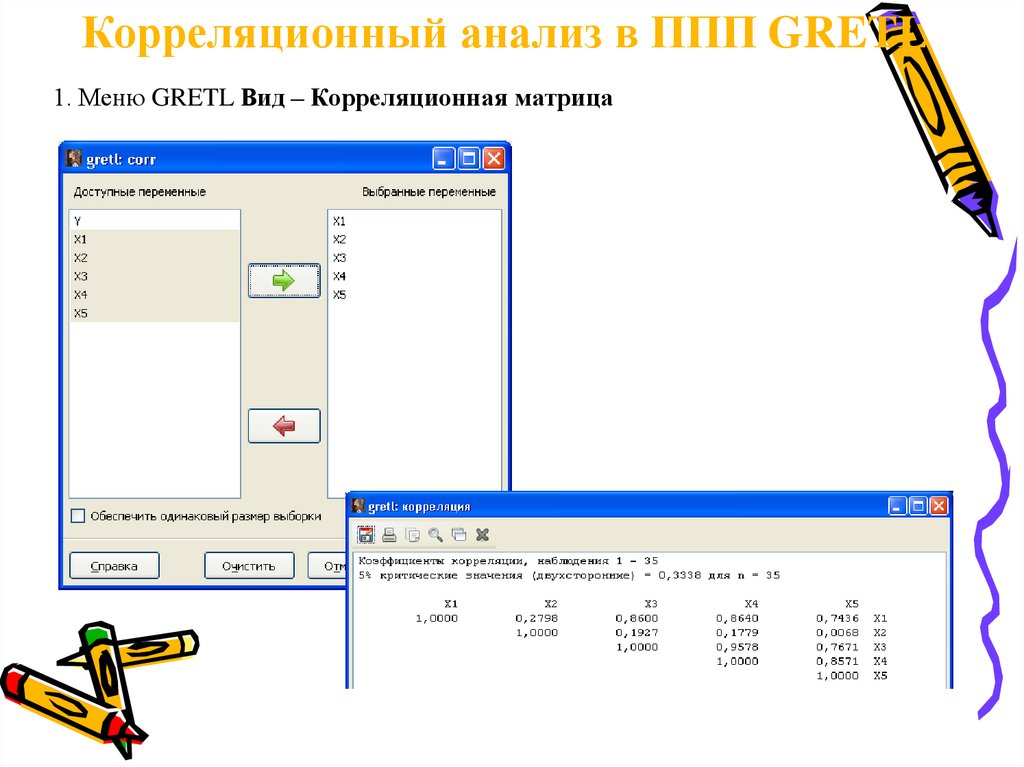
36.

Корреляционный анализ в ППП GRETL
1. Меню GRETL Вид – Корреляционная матрица