Математическая статистика. Лекция 1. Основные понятия математической статистики

1.

Математическая статистика
Пастухова Ю.И.

2.

Лекция 1
основные понятия математической
статистики
• 1. задачи математической статистики
• 2.виды выборок
• 3. Способы отбора
• 4. Статистическое распределение выборки
• 5. Эмпирическая функция распределения6.
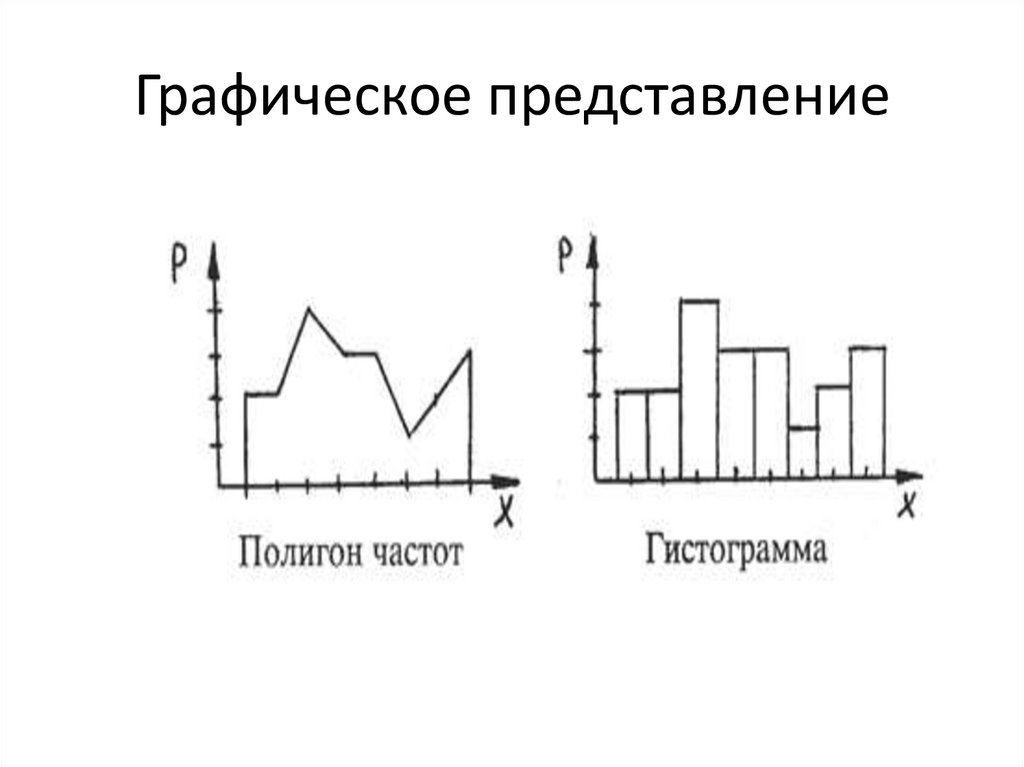
Полигон и гистограмма

3.

• 6. Числовые характеристики вариационного
ряда
• 7. Числовые характеристики вариационного
ряда
Математическая статистика – раздел
математики, посвященный методам сбора,
анализа и обработки результатов
статистических наблюдений.

4.

5.

Вариационный ряд
Признак
X1
…
Xk
Частота
n1
…
nk

6.

Графическое представление

7.

8.

Лекция 2
основные понятия теории
статистического оценивания
• 1. Понятие статистической оценки
• 2. достаточные статистики
• 3. Функция потерь
• 4. функция риска. Среднеквадратический
риск
• 5. Состоятельные оценки

9.

Точечная оценка
Оценку ̂ неизвестного параметра нужно
рассматривать как некоторую функцию
ˆ ˆ ( X1 , X 2 ,..., X n ) элементов выборки. Такие
̂
функции называются выборочными функциями
или статистиками. Значения статистики
меняются от выборки к выборке случайным
образом, поэтому статистика ˆ ( X 1 , X 2 ,..., X n )
является случайной величиной.

10.

Достаточная статистика
для семейства распределений
вероятностей {Pθ; θ ∈ Θ} или для параметра
θ ∈ Θ - статистика (векторная случайная
величина) такая, что для любого события А
существует вариант условной вероятности
Pθ(A|X = x), не зависящий от θ. Это
эквивалентно требованию, что условное
распределение любой другой статистики Y
при условии Х = х не зависит от θ.

11.

Функция потерь.
Пусть A – множество, которому принадлежит
оцениваемый параметр (параметрическое
множество.
Функция потерь W – функция, определенная на
множестве AxA, обладающая свойствами:
1.W(u,v)=w(u-v)
2. Функция w(u) определена и неотрицательна
на множестве Rk где k – размерность
параметрического множества, причем w(0)=0,
непрерывна при u=0 и отлична от
тождественного нуля.

12.

3. Функция w симметрична, т.е. w(u)=w(-u).
4. Множества {u:w(u)<c} выпуклы при всех c>0.
4'. Множества {u:w(u)<c} выпуклы при всех c>0 и
ограничены при всех достаточно малых c>0.
Чаще всего ис пользуют квадратическую
функцию потерь w(u,v)=(u-v)2.
Риском называется математическое ожидание
(среднее по всевозможным значениям
выборки) функции потерь. Риск для
квадратической функции потерь называется
среднеквадратическим риском.

13.

Состоятельные оценки
ˆ ( X , X ,..., X )
Оценка
параметра
1
2
n
называется
состоятельной,
если
при
увеличении объема n выборки она сходится по
вероятности к параметру , то есть для
любого 0
lim P ˆ ( X 1 , X 2 ,..., X n ) 1
n
.

14.

Лекция 3
Виды статистических оценок
• 1. Смещенные и несмещенные оценки
• 2. Примеры несмещенных и смещенных
оценок
• 3 Эффективные оценки

15.

Смещенные и несмещенные оценки
Оценка ̂ называется несмещенной, если ее
математическое ожидание равно оцениваемому
параметру,
то
M [ ˆ ] b( )
есть
M [ ˆ ] .
Разность
называется
смещением.
Требование
несмещенности
устраняет
систематические ошибки в определении оценок,
обусловленные ограниченным объемом выборки.
M [( ˆ ) 2 ] D[ ˆ ] b 2 ( ) .
Отсюда видно, что для несмещенных оценок
среднеквадратическая ошибка совпадает с
дисперсией оценки.

16.

Пример несмещенной оценки
Пусть ( X 1 , X 2 ,..., X n ) – выборка объема n
из генеральной совокупности с функцией
FX ( x)
распределения
и
числовыми
характеристиками M [ X ] m и.
1
1 n
1 n
M [ X ] M X k M [ X k ] nM [ X ] M [ X ] m
n
n k 1 n k 1
Это означает, что выборочное среднее X –
несмещенная
оценка
математического
2
D
[
X
]
ожидания.

17.

Пример смещенной оценки
Несложно
проверить,
что
выборочная
дисперсия является смещенной оценкой
дисперсии случайной величины X . Для
получения несмещенной оценки выборочную
дисперсию исправляют, умножая ее на n n 1 .
Исправленная выборочная дисперсия имеет вид
n
1
2
S02
(
X
X
)
k
n 1 k 1
и является
дисперсии.
уже
несмещенной
(2)
оценкой

18.

19.

Лекция 4
методы построения состоятельных
оценок
1. Метод моментов
Этот метод был предложен К. Пирсоном и
является исторически первым общим методом
построения оценок и срстоит в следующем
Будем предполагать, что у случайной величины
существуют первые k моментов mi =M ( i ), i
=1,…k. Так как закон распределения известен с
точностью до параметров 1, 2,…, k ,
величины mi будут функциями параметров 1,
2,…, k , то есть
mi = f i ( 1, 2,…, k) , i=1,…,k
(1)

20.

Предположим, что система уравнений (1)
разрешима относительно 1, 2,…, k , то
есть существуют такие функции i(m1,
m2,,…, mk ), i = 1,…,k , что
I = i(m1, m2,,…, m) k ), i = 1,…,k.
Вычислим mi* = (1/n)
, i=1,…,k.
Тогда вектор n=( n,1, n,2,…, n,k , где
i= i(m1*, m2*,,…, mk* ), будет представлять
собой значение оценки по методу
моментов неизвестных параметров 1, 2,…,
k в распределении
F =(x, 1, 2,…, k).

21.

2. Метод максимального правдоподобия
Плотность распределения выборочной совокупности
( X 1 , X 2 ,..., X n ) в силу независимости составляющих можно
записать в виде
p X1 , X 2 ,..., X n ( x1 , x2 ,..., xn , ) p X ( x1 , ) p X ( x2 , )... p X ( xn , ) .
Если X – дискретная случайная величина и вероятность
P{ X xi } p( xi , ) i 1, 2,..., n есть функция неизвестного
параметра , то вероятность при n независимых наблюдениях
получить
выборку
( x1 , x2 ,..., xn )
вероятностей P{ X xi } , то есть
равна
произведению
P{ X x1 , X x2 ,..., X xn } p( x1 , ) p( x2 , )... p( xn ,
и также является функцией лишь аргумента .

22.

Функция L( x1 , x2 ,..., xn , ) , определяемая
соотношением
n
L( x1 , x2 ,..., xn , ) p( xk , ) p( x1 , ) p( x2 , )... p( xn , )
k 1
где p( xk , ) – плотность распределения для
непрерывной случайной величины и вероятность
принять значение x для дискретной случайной
величины, называется функцией правдоподобия.
k
,

23.

• Метод максимального правдоподобия
состоит в том, что в качестве оценки
неизвестного параметра принимается
значение , доставляющее максимум
функции правдоподобия, то есть то
значение , при котором вероятность
получения данных значений выборки
максимальна.
L( ˆ 1 , ˆ 2 ,..., ˆ k )
max
( 1 , 2 ,..., k )
L( 1 , 2 ,..., k )
• Оценки, полученные с помощью этого
метода, называются оценками
максимального правдоподобия или
сокращенно МП-оценками.

24.

Лекция 5
Интервальное оценивание
1.Идея интервального оценивания
2. Понятие доверительного интервала
3. Методы построения доверительных
интервалов
4.Примеры доверительных интервалов
5. Интервалы правдоподобия и толерантные
интервалы

25.

Можно построить такой интервал, внутри
которого с заданной вероятностью находится
точное значение оцениваемого параметра.
Такой подход к задаче оценивания параметров
называют интервальным оцениванием.
Интервальное оценивание особенно
актуально в тех случаях, когда объем выборки
мал и использование точечных оценок может
привести к значительным ошибкам.
Интервал, содержащий истинное значение
параметра с заданной вероятностью ,
называется доверительным интервалом для
оцениваемого параметра.

26.

При интервальном оценивании строят две такие
статистики 1 ( X 1 , X 2 ,..., X n ) и 2 ( X 1 , X 2 ,..., X n ) , для
которых при заданном значении вероятности выполняется
условие
P{ 1 ( X 1 , X 2 ,..., X n ) 2 ( X 1 , X 2 ,..., X n )} 1 .
(7)
] 1 ; 2 [ , содержащий истинное значение
параметра с заданной вероятностью 1 , называется
Интервал
доверительным интервалом для параметра
1
Число
называется
.
вероятностью (надежностью), а число
значимости.
доверительной
– уровнем

27.

• Толерантные пределы можно рассматривать
как критические значения случайной
величины Х, построенные по большому
количеству выборок наблюдений. Например,
исходя из конкретной выборки измерений
роста мужчин, мы с вероятностью (1-a) = 0.95
нашли двусторонние границы толерантного
интервала, при которых рост у Р = 99% мужчин
будет не меньше Lt и не больше Ut. Это
означает, что при взятии повторных выборок
выполненные измерения могут выйти за эти
пределы, но это будет иметь место менее, чем
в 5% случаев.

28.

• Отметим, что задаваемая доля Р
вероятностной меры (как и граничные
значения Lt и Ut ) является случайной
величиной, в чем принципиальное отличие
толерантного интервала от доверительного,
который строится относительно постоянной
величины – параметра

29.

• Интервалы правдоподобия. Подход,
развитый в предыдущих разделах, наводит
на мысль, что значение , такое, что
отношение L( )/L( max) лишь немногом
менее правдоподобным, чем max, в то
время как значение , для которого
L( )/L( max) много меньше единицы,
является намного мене правдоподобным,
чем max .

30.

• Определение Интервалы правдоподобия
(один параметр). Для данных X1,…,Xn ,
совместное выборочное распределение
которых зависит от единственного параметра
, обозначим функцию правдоподобия через
L( ). Если существуют такие значения 1 и 2 ,
что
L( )/L( max) 0,10
для 1< < 2 , то интервал называется 10% ным интервалом правдоподобия для данной
выборки (аналогично для интервалов других
процентных уровней

31.

Лекция 6
основные понятия теории проверки
статистических гипотез
• 1. Статистическая гипотеза. статистические
критерии
• 2. Критерии значимости простой нулевой
гипотезы
• 3. Область значимости, уровень значимости
• 4. Ошибки

32.

• Пример:
• Увеличение числа заболевших некоторым
заболеванием дает возможность выдвинуть
гипотезу о наличии эпидемии. Для сравнения
доли заболевших в обычных и экстремальных
условиях используются статистические
данные, на основании которых делается вывод
о том, является ли данное массовое
заболевание эпидемией. Предполагается, что
существует некоторый критерий- уровень доли
заболевших, критический для этого
заболевания, который устанавливается по
ранее имевшимся случаям.

33.

• Статистическая гипотеза- это утверждение
о виде неизвестного распределения или
параметрах известного распределения.
Статистические гипотезы проверяются по
результатам выборки статистическими
методами
в
ходе
эксперимента
(эмпирическим
путем)
с
помощью
статистических критериев.

34.

• В тех случаях, когда известен закон
распределения генеральной совокупности, но
неизвестны
значения
его
параметров
(дисперсия или математическое ожидание) в
конкретной ситуации, статистическую гипотезу
называют параметрической
• Когда закон распределения генеральной
совокупности не известен, но есть основания
предположить, каков его конкретный вид,
выдвигаемые
гипотезы
о
виде
его
распределения
называются
непараметрическими.

35.

• Критерии значимости (или критерии
проверки гипотез) – это, возможно.
простейшие, но наиболее широко
используемые статистические средства.
• Ключевыми понятиями являются область
значимости и уровень значимости.

36.

Порядок построения критерия
• Вероятностная модель (подбор данных и их
анализ)
• Сокращение данных. Статистика критерия
(данные сводятся в одну статистику).
• Нулевая гипотеза (чаще всего предположение о согласованности данных со
значениями параметров). Нулевое
распределение (распределение статистики
критерия при условии справедливости
гипотезы).

37.

• Альтернативная гипотеза
• Согласованности выборки с гипотезой
• Область значимости (множество
значений статистики критерия, выбираемое
так, что когда гипотеза верна, то и его
вероятность мала), уровень значимости
(вероятность значимости0. Критическая
область (условное множество значимости,
которое при фактических наблюдени0х
имеет довольно низкий уровень
значимости, например =0,05).

38.

Лекция 7
Проверка статистических критериев
• Схема применения статистического критерия
• Параметрические критерии.Сравнение
средних и дисперсий
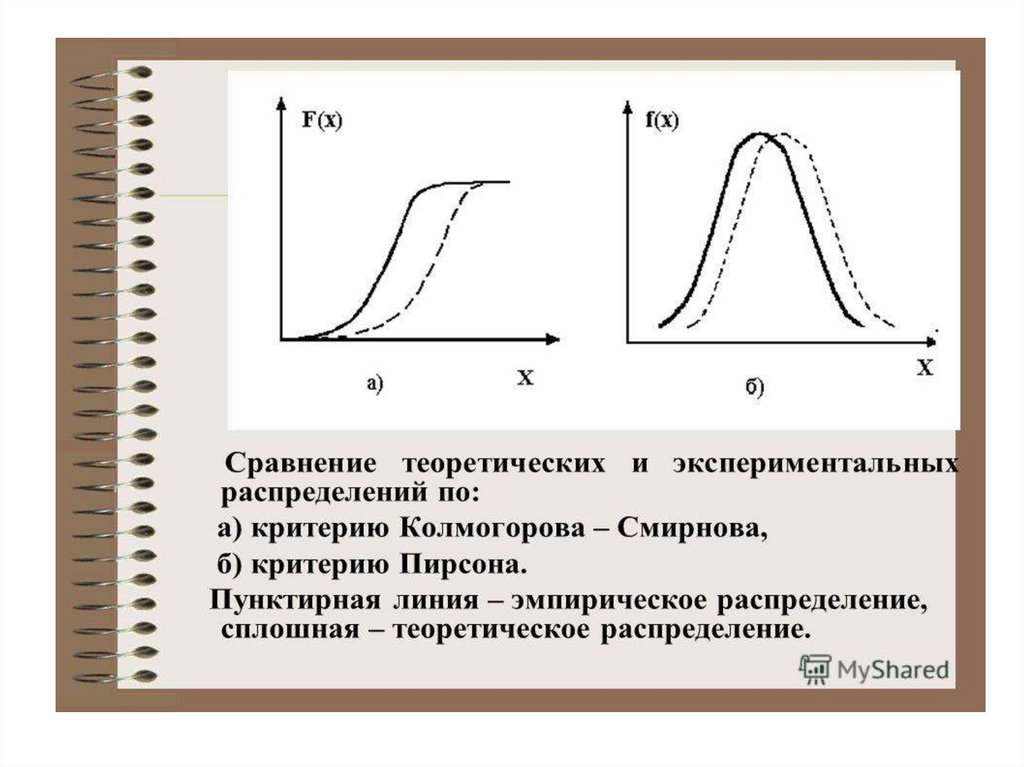
• Критерии согласия (проверки гипотезы о виде
распределения генеральной совокупности)
• Критерий Колмогорова (Колмогорова –
Смирнова)
• Критерий согласия Пирсонек

39.

• Процедура проверки гипотез обычно проводится по
следующей схеме:
• Формулируются гипотезы Н0 и Н1.
• Выбирается уровень значимости критерия a.
• По выборочным данным вычисляется значение
некоторой случайной величины K, называемой
статистикой критерия, или просто критерием, который
имеет известное стандартное распределение
(нормальное, Т-распределение Стьюдента и т.п.)
• Вычисляется критическая область и область принятия
гипотезы. То есть находится критическое (граничное)
значение критерия при уровне значимости a, взятым из
соответствующих таблиц.
• Найденное значение Kнабл критерия сравнивается с
Ккритич и по результатам сравнения делается вывод:
принять гипотезу или отвергнуть.

40.

• Если вычисленное по выборке значение
критерия Kнабл меньше чем Ккритич, то гипотеза
Но принимается на заданном уровне
значимости a. Однако принятие гипотезы Н0
совсем не означает доказательства равенства
параметров генеральных совокупностей.
Просто имеющийся в распоряжении
статистический материал не дает оснований
для отклонения гипотезы о том, что эти
параметры одинаковы. Возможно, появится
другой экспериментальный материал, на
основании которого эта гипотеза будет
отклонена.)

41.

• Если вычисленное значение критерия Kнабл больше
Ккритич, то гипотеза Н0 отклоняется в пользу
альтернативной гипотезы Н1 при данном уровне
значимости .
• Целью первичной обработки экспериментальных
наблюдений обычно является выбор закона
распределения, наиболее хорошо описывающего
случайную величину, выборку которой наблюдают.
Насколько хорошо наблюдаемая выборка описывается
теоретическим законом, проверяют с помощью
различных критериев согласия. Цель проверки гипотезы
о согласии опытного распределения с теоретическим –
это стремление удостовериться в том, что данная
модель теоретического закона не противоречит
наблюдаемым данным, и использование ее не
приведет к существенным ошибкам при вероятностных расчетах.

42.

43.

44.

45.

46.

47.

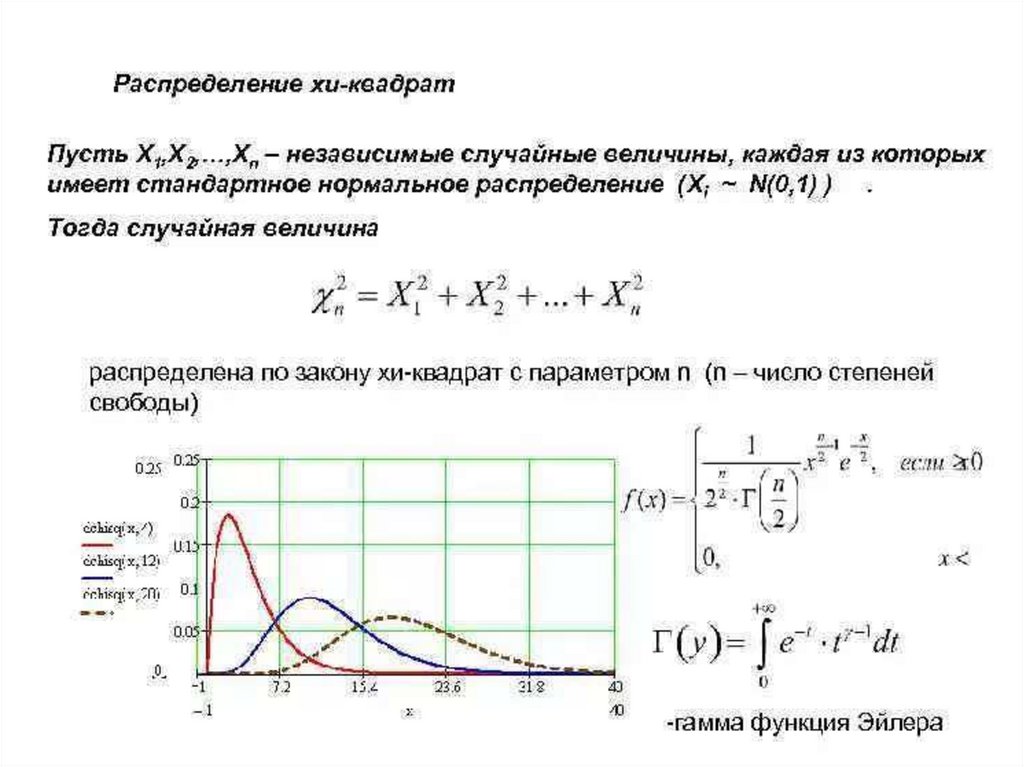
Лекция 8
Критерии, основанные
на статистике 2
• Распределение 2
• Критерий однородности
• Критерий годности подбора
• Критерии контингенции

48.

49.

50.

Запишем алгоритм проверки гипотезы
оододнородности с помощью критерия 2:
• 1. По выборкам X1, …, Xk строим вектор
наблюдаемых значений Y.
• 2. Для каждого исхода Y1, …, Ys вычисляем число его
реализа-ций в j-й серии.
• 3. Получаем оценки вероятностей p1, …, ps по
формуле (6.1).
• 4. Вычисляем значение статистики 2 по формуле .
• 5. По заданному уровню значимости α найдем C(α)
из условия 2(s-1)(k-1)(C(α)) =1- α
• 6. Гипотезу однородности принимаем, если
• 2 < C(α) и отклоняем в противном случае.

51.

• Таблицы сопряженности могут принимать
различные формы, простейшая таблица
сопряженности выглядит следующим
образом:
Фактор риска есть
Фактора риска нет
Всего
Исход есть Исхода нет Всего
A
C
A+C
B
D
B+D
A+B
C+D
A+B+C+D

52.

• Тип данных: параметры должны быть
качественными цельночисленными частотами,
измеренными в номинальной шкале (Например,
тип диагноза)
• бинарными (пол: мужской/женский, наличие или
отсутствие заболевания)
порядковыми (степень артериальной гипертензии),
• Желательно, чтобы общее количество наблюдений
было более 20,
• Ожидаемая частота, соответствующая нулевой
гипотезе должна быть более 5, если ожидаемое
явление принимает значение менее 5, то
необходимо использовать точный Критерий
Фишера.

53.

• Для четырехпольных таблиц (2х2): Если ожидаемое
значение принимает значение менее 10 (а именно
5<x<10), необходим расчет поправки Йетса таблиц
сопряженности
• Сравниваемые частоты должны быть примерно
одного размера
• Сопоставляемые группы должны быть
независимыми (то есть единицы наблюдения в них
разные, в отличие от связанных групп,
анализирующих изменения «до-после» у одних и
тех единиц наблюдений до и после вмешательства.
Для таких ситуаций существует отдельный тест
МакНемара (McNemar)
• Запрещается: использовать хи-квадрат для анализа
непрерывных абсолютных данных, процентов и
долей.

54.

Лекция 9
Порядковые статистики. Критерии,
основанные на рангах
• Порядковые статистики
• Критерий медианы
• Ранги
• Некоторые ранговые критерии

55.

56.

• Медианный критерий. Статистика критерия
строится следующим образом. Находится
медиана общего упорядоченного ряда и
подсчитывается число наблюдений
выборки , превосходящих медиану (если
нечетно и медиана принадлежит выборке ,
то это число увеличивается на 1/2). Тогда
статистика критерия может быть записана
как. , где.

57.

• Определение. Рангом наблюдения
называют тот номер, который получит
это наблюдение в упорядоченной
совокупности всех данных — после их
упорядочения по определенному правилу
(например, от меньших значений к
большим или наоборот).
• Определение. Процедура перехода от
совокупности наблюдений к
последовательности их рангов
называется ранжированием. Результат
ранжирования называется ранжировкой

58.

59.

60.

Лекция10
Линейная корреляция
• Коэффициент корреляции. Свойства
• Значимость коэффициента корреляции
• Доверительный интервал для
коэффициента корреляции
• Ранговый коэффициент корреляции
Спирмана. Значимость
• Коэффициент ранговой корреляции
Кендэла

61.

62.

63.

64.

• Построение доверительного интервала для
коэффициента корреляции
• Распределение выборочного коэффициента
корреляции сложное, поэтому часто пользуются
преобразованием Фишера для аппроксимации
точного распределения коэффициента корреляции.
• При больших значениях n распределение
выборочного коэффициента корреляции r
стремится к нормальному z.
• Преобразование Фишера:
• Z=0.5ln((1+r)/(1-r))
• Для преобразованного z стандартная ошибка
среднего равна σ=(n-3)1/2

65.

66.

67.

68.

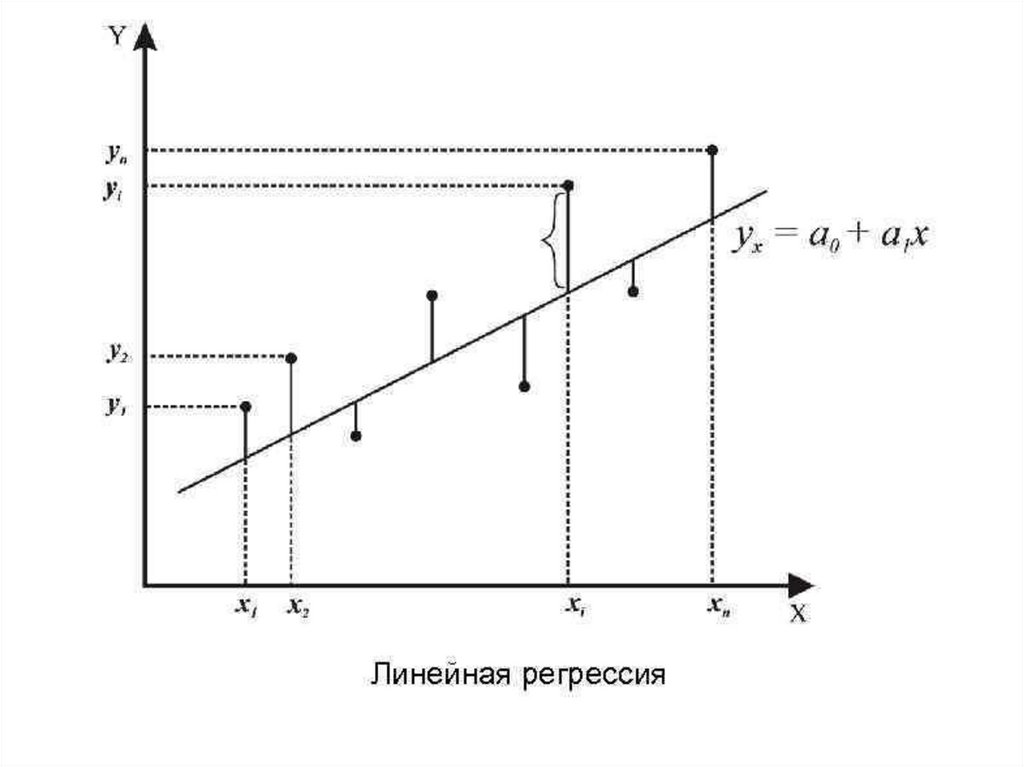
Лекция 11
Линейная регрессия. Метод
наименьших квадратов
• Линейная регрессия
• Оценка параметров. Метод наименьших
квадратов
• Значимость уравнения регрессии
• Нелинейнвя регрессия. Линеаризация

69.

• Регрессия — способ выбрать из семейства
функций ту, которая минимизирует
функцию потерь. Последняя характеризует
насколько сильно пробная функция
отклоняется от значений в заданных точках.
Если точки получены в эксперименте, они
неизбежно содержат ошибку измерений,
шум, поэтому разумнее требовать, чтобы
функция передавала общую тенденцию, а
не точно проходила через все точки.

70.

71.

72.

73.

74.

Лекция 12
Множественная регрессия
• Линейная множественная регрессия
• Матричный метод наименьших квадратов
• Теорема Гпусса - Маркова
• Проверка значимости коэффициентов
линейной множественной регрессии
• Проверка значимости уравнения
множественной регрессии
• Полиномиальная регрессия

75.

Множественной регрессией называется
условное математическое ожидание
переменной Y как функция от переменных
X2,…,Xk. Модель множественной линейной
регрессии имеет вид:
Yi = β0 + β1 X1i + ... + βk Xki +εi , i = 1,…, n,
где n – число наблюдений, X1 ,..., Xk независимые переменные, Y – зависимая
переменная, ε – лучайная составляющая, β0 ,β1
,...,βk - коэффициенты регрессии.
Для нахождения оценок параметров β0 ,β1 ,...,βk
используется метод наименьших квадратов
(МНК), сводящийся к минимизации β0 ,β1 ,...,βk
суммы квадратов отклонений

76.

77.

78.

79.

Пусть m – число переменных в линейном уравнении
регрессии, тогда статистика Фишера F имеет вид:

80.

81.

Лекция 13
Основы множественного
корреляционного и регрессионного
анализа
• Частные коэффициенты детерминации
• Корреляционная матрица
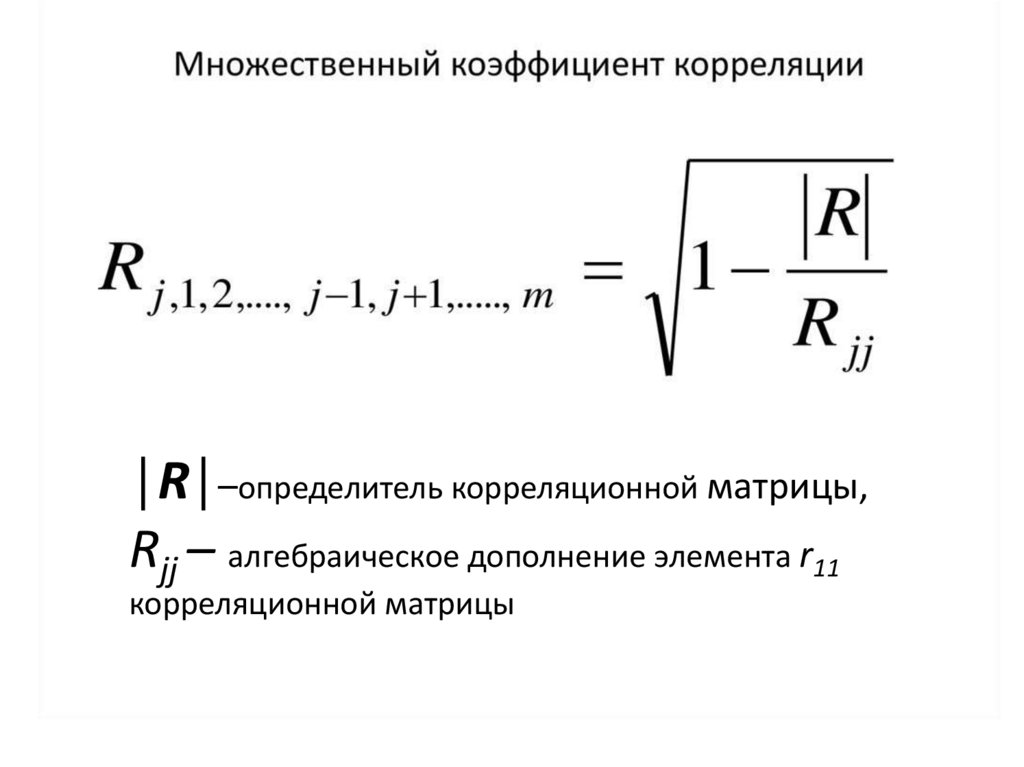
• Множественный коэффициент корреляции
• Частные коэффициенты корреляции

82.

Частный коэффициент детерминации:

83.

84.

│R│–определитель корреляционной матрицы,
Rjj – алгебраическое дополнение элемента r11
корреляционной матрицы

85.

86.

87.

88.

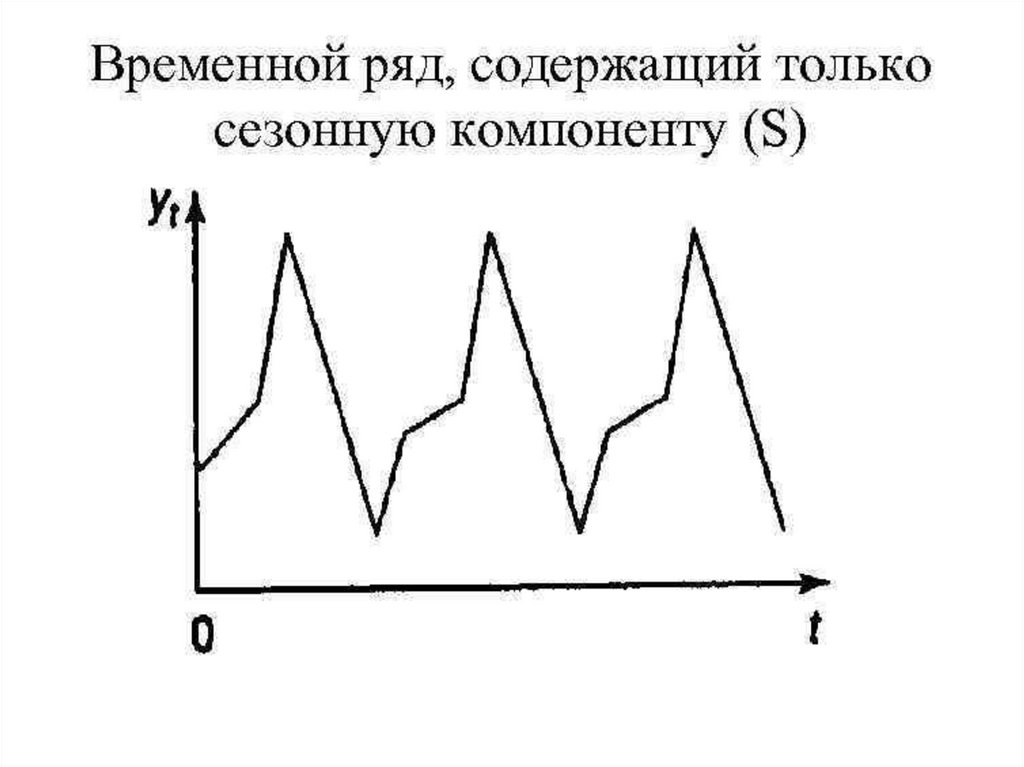
Лекция 14
Временные ряды
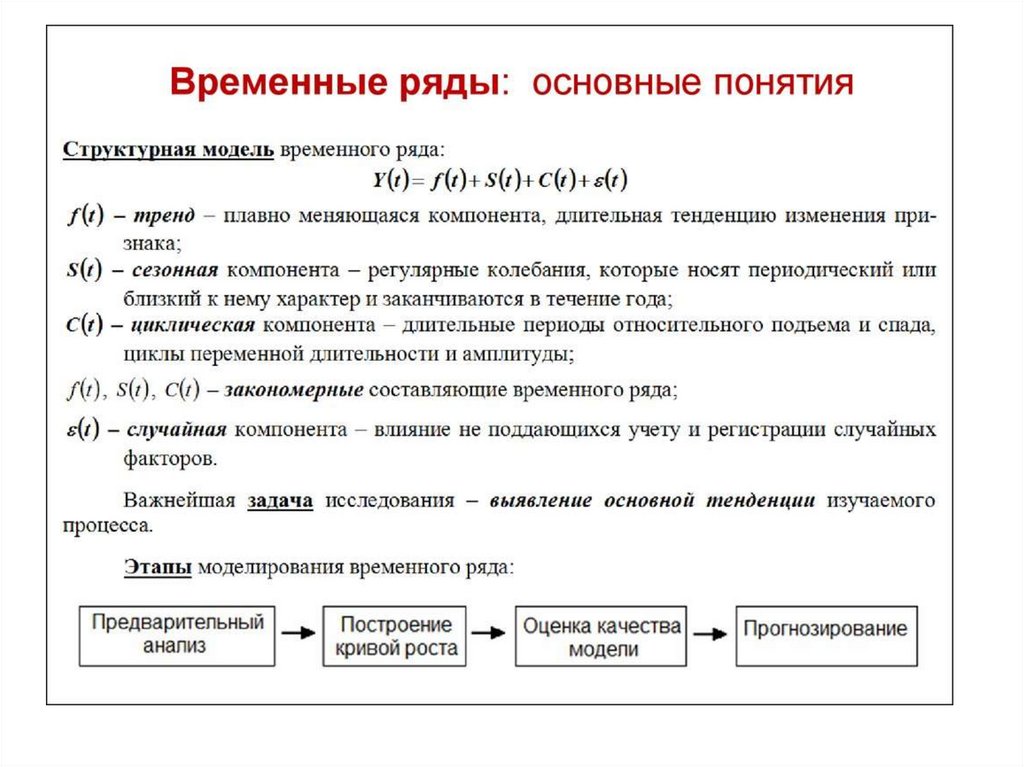
• Основные понятия теории временных
рядов
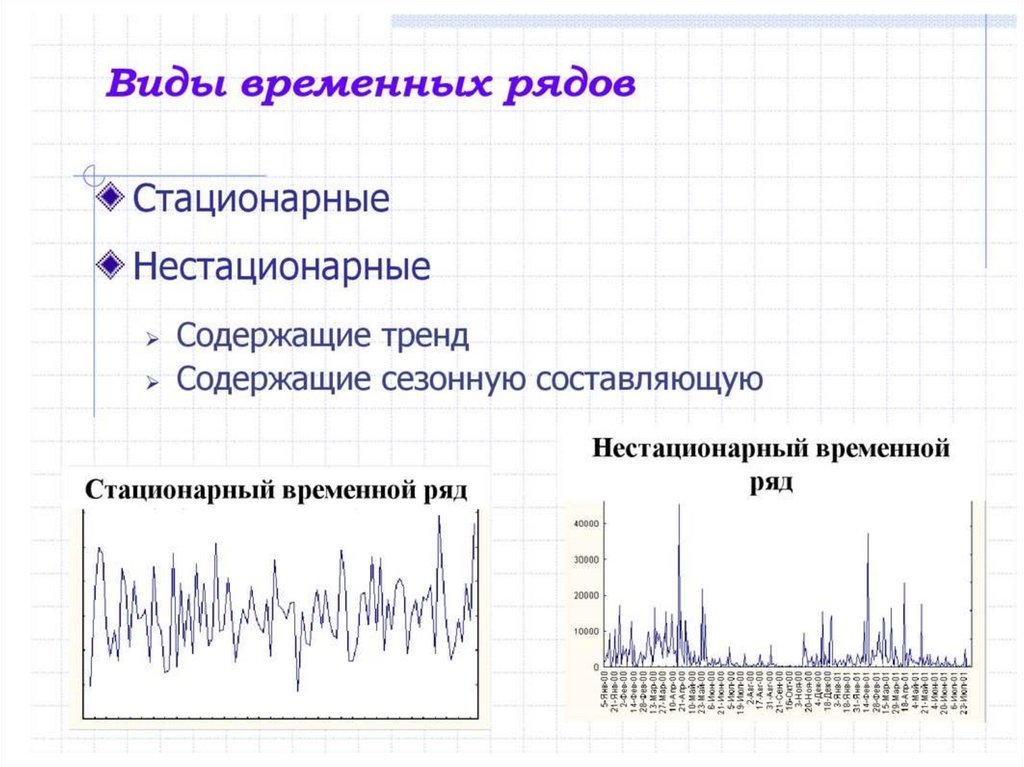
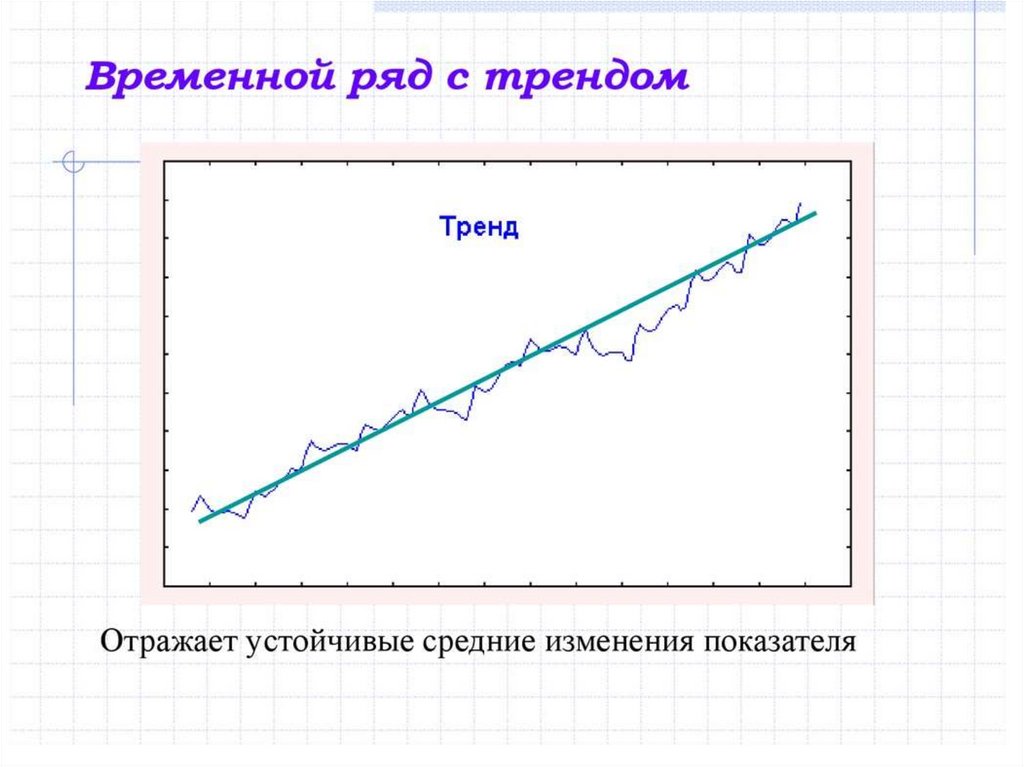
• Тренд. Сезонность
• Стационарные временные ряды
• Автокорреляция
• Модель авторегрессии

89.

90.

91.

92.

93.

94.

95.

96.

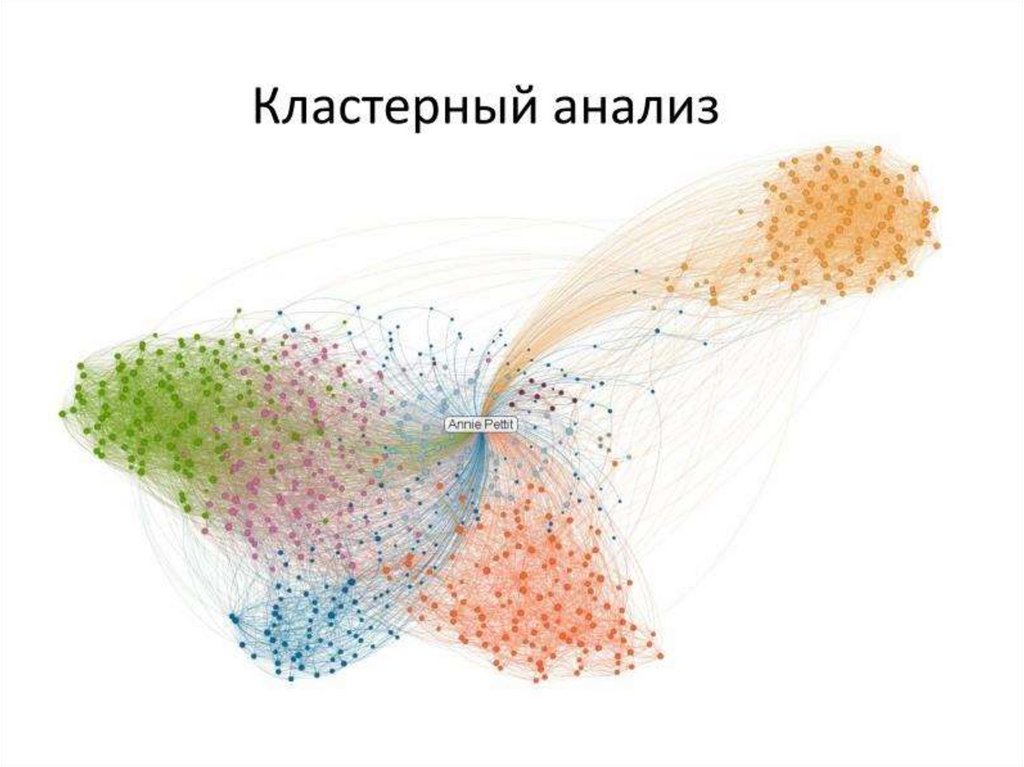
Лекция 15
элементы кластерного анализа
• Цели и задачи
• Кластеры. Алгоритмы кластеризации
• Этапы кластерного анализа
• Описание элементов
• Расстояния между элементами
• Метод k-средних

97.

98.

99.

100.

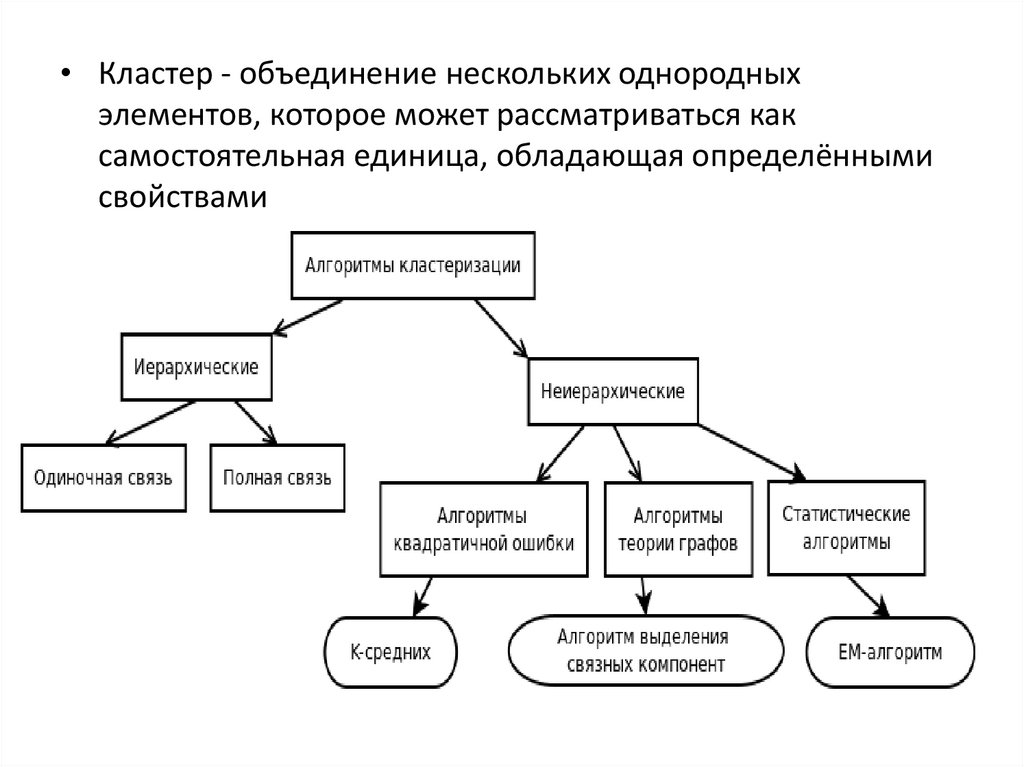
• Кластер - объединение нескольких однородных
элементов, которое может рассматриваться как
самостоятельная единица, обладающая определёнными
свойствами

101.

102.

Метод k-средних
Наиболее популярный метод
кластеризации. Был изобретён в 1950-х
годах математиком Гуго Штейнгаузом и
почти одновременно Стюартом Ллойдом .
Действие алгоритма таково, что он
стремится минимизировать суммарное
квадратичное отклонение точек кластеров
от центров этих кластеров:

103.

Алгоритм k-средних
• 1) Выбрать k случайных центров в
пространстве, содержащем исходные данные
2) Приписать каждый объект из множества
исходных данных кластеру исходя из того,
какой центр к нему ближе
3) Пересчитать центры кластеров используя
полученное распределение объектов
4) Если алгоритм не сошелся, то перейти к п. 2.
Типичные критерии схождения алгоритма это
либо среднеквадратичная ошибка, либо
отсутствие перемещений объектов из кластера
в кластер.

104.

Лекция 16
Иерархические алгоритмы
кластеризации
• Типы алгоритмов иерархической
кластеризации
• Расстояния между объектами. Матрица
расстояний
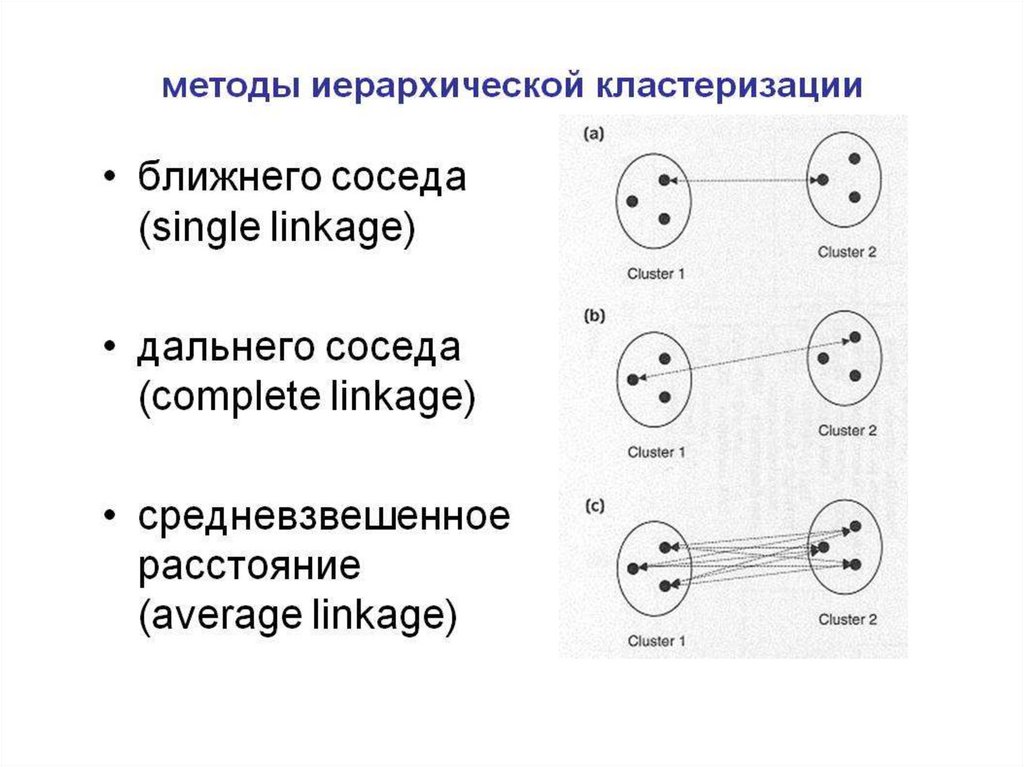
• Расстояния между кластерами
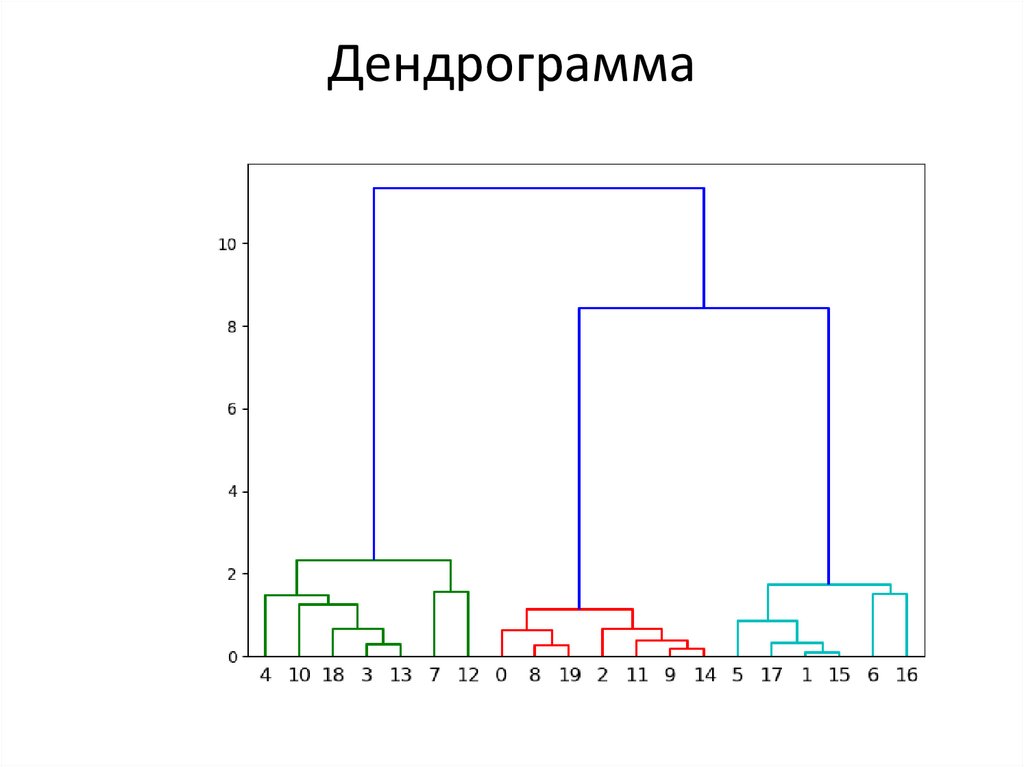
• Дендрограммы

105.

• По своему подходу, все алгоритмы
иерархической кластеризации делятся на
два типа: сверху-вниз и снизу-вверх.
Первые начинают с одного большого
кластера состоящего из всех элементов, а за
тем, шаг за шагом разбивают его на все
более и более мелкие кластеры. Вторые,
напротив, начинают с отдельных элементов
постепенно объединяя их в более и более
крупные кластеры.

106.

• Матрица расстояний — это матрица n x n,
которая содержит значения меры
расстояния/сходства между объектами в
метрическом пространстве. Существует
множество мер расстояния/сходства, выбор из
которых зависит от типа данных. К сожалению, не
существует универсального правила выбора.

107.

108.

109.

Дендрограмма