Основные определения теории проверки гипотез

1. Основные определения теории проверки гипотез

Пусть имеется выборка X 1 , X 2 ,... X n из генеральной совокупности с
неизвестной теоретической функцией распределения.
Определение: Статистической гипотезой называется любое
предположение о виде теоретической функции распределения, то есть
статистическая гипотеза – это рассматриваемое предположение о
величине параметра генеральной совокупности.. Имеются две
непересекающиеся гипотезы: Н0 и H1. Н0 – нулевая (основная) гипотеза,
H1 – альтернативная (конкурирующая) гипотеза. Принято считать, что Н0
–гипотеза о сходстве, H1 –гипотеза о различии.
• Нулевая гипотеза – это допущение, которое считается верным до тех
пор, пока не будет доказано обратное, исходя из результатов
статистической проверки.
• Альтернативная гипотеза – это гипотеза, которая принимается, если в
результате статистической проверки отвергается нулевая гипотеза.
Лекция №3, Статистическое
моделирование, Лакман И.А.
1

2. Основные определения теории проверки гипотез

Определение: Статистическим критерием (тестом) называется
правило, позволяющее на основании наблюдений X 1 , X 2 ,...X n принять
нулевую гипотезу Н0 или отвергнуть ее в пользу альтернативной H1.
Проверка гипотезы может быть односторонней или двусторонней.
Определение: Односторонний критерий используется в тех случаях,
когда необходимо знать, является ли параметр генеральной совокупности
> (правосторонний критерий) или < (левосторонний критерий)
предполагаемого значения.
Определение: Двусторонний критерий используется в тех случаях,
когда интересует, отличаются ли реальные значения параметра от
предполагаемого значения.
Определение: Критическую область составляют те значения
выборочных статистических показателей, которые ведут к отказу от
нулевой гипотезы.
Лекция №3, Статистическое
моделирование, Лакман И.А.
2

3. Уровень значимости

Определение: Уровень значимости – вероятность ошибочного
отклонения нулевой гипотезы Н0 (вероятность ошибки I рода). При
статистическом анализе исследователь должен выбрать необходимый
уровень значимости. При этом считают низшим уровнем значимости
значение α=0.05, достаточным уровнем - α=0.01, высшем уровнем α =0.001.
Иногда, доверительной вероятностью считается величина р=1- α
Возможные решения статистического критерия:
Результат
проверки
гипотезы
Н0 отклоняется
Н0
отклоняется
не
Возможные состояния проверяемой
гипотезы
Верна гипотеза
Верна гипотеза
Н0
H1
Ошибка I рода
Правильное
решение
Правильное
решение
Лекция №3, Статистическое
моделирование, Лакман И.А.
Ошибка II рода
3

4. Ошибки I и II рода

Определение 1: В процессе проверки гипотезы существует вероятность
того, что Н0 будет отвергнута, когда в действительности она должна быть
принята. Это называется ошибкой первого рода. Вероятность допущения
ошибки первого рода это уровень значимости. Таким образом, когда
выбирают 5% уровень значимости для проверки, одновременно допускают,
что в 5% случаев должны отвергнуть Н0, хотя она и верна.
Определение 2: Второй вид ошибок имеет место при принятии нулевой
гипотезы, в то время как в действительности она должна быть
отвергнута.такая ошибка называется ошибкой второго рода.
Действительность
Р
Е
Ш
Е
Н
И
Е
Н0 - верна
Обвиняемый
невиновен
Н0 - принята
Обвиняемый
освобожден
Х
Ошибка I рода
Н0 - отвергнута
Обвиняемый
Лекция №3, Статистическое
наказан
моделирование, Лакман И.А.
Н0 - ложна
Обвиняемый
виновен
Ошибка II рода
Х
4

5. Этапы принятия статистического решения

1.
2.
3.
4.
5.
6.
7.
8.
Формулировка нулевой и альтернативной гипотез.
Определение объема выборки.
Выбор соответствующего уровня значимости или вероятности
отклонения гипотезы Н0 ( p 0.05).
Выбор статистического метода, который зависит от типа решаемой
задачи.
Вычисление значения выборочной статистики K n K n ( X 1 , X 2 ,...X n ) на
основании наблюдений X 1 , X 2 ,...X n .
Если гипотеза Н0 верна, то распределение случайной величины K n
известно (затабулировано). Нахождение по таблице для выбранного
статистического метода критической области K для определенного
уровня значимости.
Сравнение эмпирического и критического значений. Если K n K ,
то принимается Н0; если K n K , то Н0 отвергается в пользу
альтернативной.
Формулировка принятия решения (выбор гипотезы Н0 или H1).
Лекция №3, Статистическое
моделирование, Лакман И.А.
5

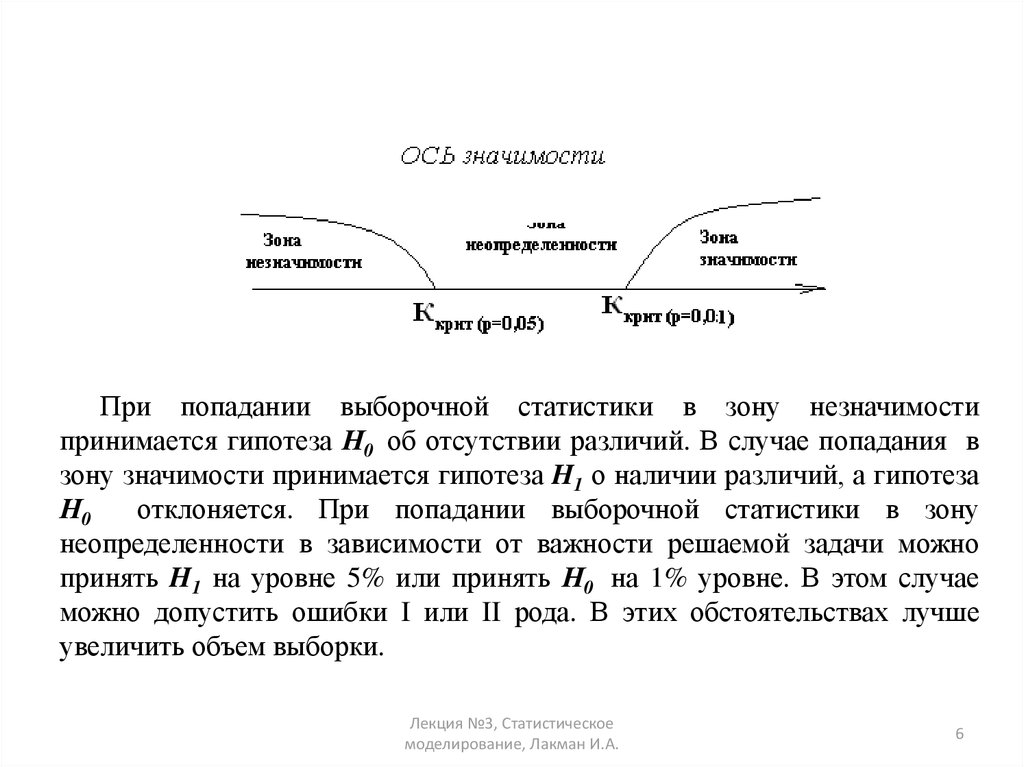
6.

При попадании выборочной статистики в зону незначимости
принимается гипотеза Н0 об отсутствии различий. В случае попадания в
зону значимости принимается гипотеза H1 о наличии различий, а гипотеза
Н0
отклоняется. При попадании выборочной статистики в зону
неопределенности в зависимости от важности решаемой задачи можно
принять H1 на уровне 5% или принять Н0 на 1% уровне. В этом случае
можно допустить ошибки I или II рода. В этих обстоятельствах лучше
увеличить объем выборки.
Лекция №3, Статистическое
моделирование, Лакман И.А.
6

7. Проверка гипотезы о соответствии исправленной выборочной дисперсии величине генеральной дисперсии нормальной совокупности

Стандартизированный статистический критерий (тест) для проверки такой
(n 1) S 2
2
расч
гипотезы рассчитывается как:
,
(1)
02
где σ02– проверяемое значение генеральной дисперсии,
а S2– исправленная выборочная дисперсия, n – объем выборки.
Левосторонняя проверка: нулевая и альтернативная гипотезы имеют
вид:
Н0: S2=σ2 – равенство неизвестной генеральной дисперсии S2;
Н1: S2<σ2.
2
2
расч
1 , k ,
Правило принятия решения: принять Н0, если
отвергнуть Н0, если 2 2
расч
,k
Здесь α – уровень значимости принятия гипотезы, k=n-1 – число
степеней свободы 12 ,k - определяется по таблице χ2–распределения.
Лекция №3, Статистическое
моделирование, Лакман И.А.
7

8. Проверка гипотезы о соответствии исправленной выборочной дисперсии величине генеральной дисперсии нормальной совокупности

Правосторонняя проверка: нулевая и альтернативная гипотезы имеют вид:
Н0: S2=σ2 – равенство неизвестной генеральной дисперсии S2;
Н1: S2>σ2.
2
2
Правило принятия решения: принять Н0, если расч , k ,
отвергнуть Н0, если 2 2 .
расч
,k
Двусторонняя проверка: нулевая и альтернативная гипотезы имеют вид:
Н0: S2=σ2 – равенство неизвестной генеральной дисперсии S2;
Н1: S2≠σ2.
2
2
2
расч
Правило принятия решения: принять Н0, если 1 , k
,
,k
2
2
отвергнуть Н0 в противном случае.
Лекция №3, Статистическое
моделирование, Лакман И.А.
8

9. Проверка гипотезы о соответствии выборочной средней величине генеральной средней нормальной совокупности

Формируем гипотезы о равенстве генеральной μ и выборочной средней
μ0 .
Н0: μ=μ0;
Н1: μ≠μ0.
x 0
zкрит ,
Правило принятия решения: принять Н0, если zкрит
2
S /n
в противном случае принять Н1.
Zкрит определяется из таблиц функции Лапласа
из равенства Ф(zкрит)=(1-α)/2.
Лекция №3, Статистическое
моделирование, Лакман И.А.
9

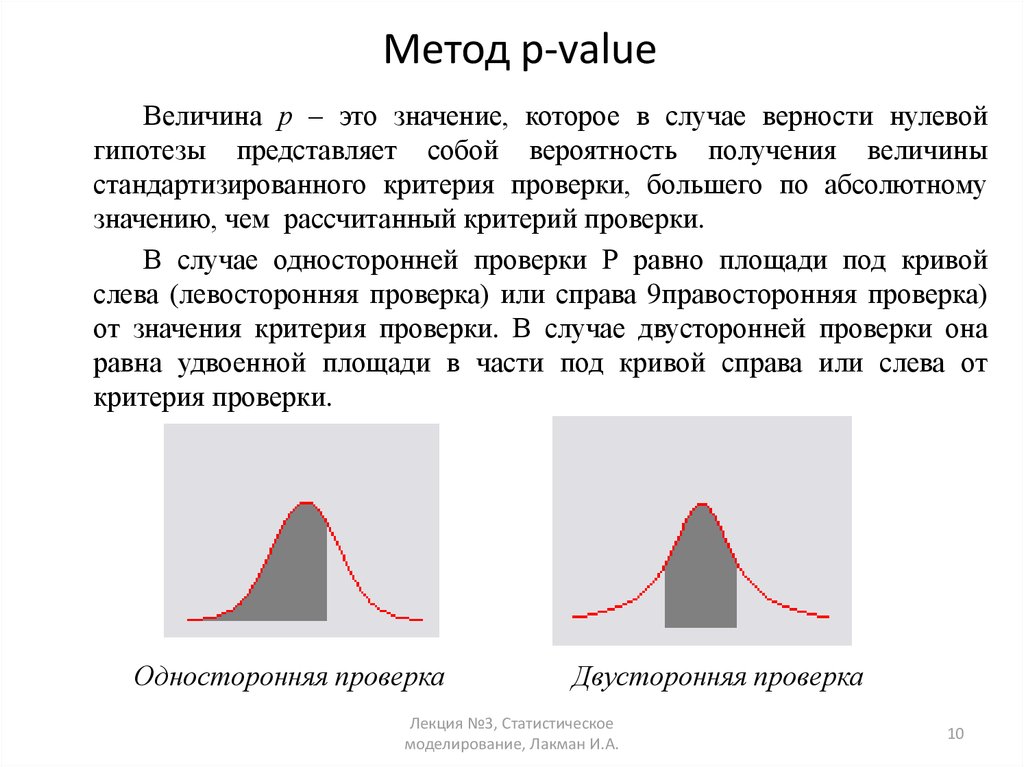
10. Метод p-value

Величина р – это значение, которое в случае верности нулевой
гипотезы представляет собой вероятность получения величины
стандартизированного критерия проверки, большего по абсолютному
значению, чем рассчитанный критерий проверки.
В случае односторонней проверки Р равно площади под кривой
слева (левосторонняя проверка) или справа 9правосторонняя проверка)
от значения критерия проверки. В случае двусторонней проверки она
равна удвоенной площади в части под кривой справа или слева от
критерия проверки.
Односторонняя проверка
Двусторонняя проверка
Лекция №3, Статистическое
моделирование, Лакман И.А.
10

11. Метод p-value

В методе p-value правило принятия решения одинаково независимо то
того, выполняется левосторонняя, правосторонняя или двусторонняя
проверка. Обозначив степень значимости для проверки через α, получим
следующее правило принятия решения:
• Принять Н0, если p-value≥ α
• В противном случае, отвергнуть Н0.
Расчет величины р:
Для того чтобы найти величину р, прежде всего рассчитывают
стандартный критерий проверки, а затем, зная число степеней свободы,
находят вероятности (площади в граничных областях), соответствующие
показателям статистики (F или t или z), которые охватывают снизу и
сверху рассчитанный критерий проверки. После этого с помощью
интерполяции, исходя из полученных вероятностей, находят величину р.
Лекция №3, Статистическое
моделирование, Лакман И.А.
11

12. Задача оценивания

Пусть имеются данные выборки, например значения некоторого
признака, Х1, Х2,…, Хn, полученные в результате n наблюдений. Для
того чтобы найти статистическую оценку θ неизвестного
параметра теоретического распределения через эти данные
необходимо найти функцию от наблюдаемых случайных величин,
которые дают приближенное значение оцениваемого параметра.
Статистическую оценку, которая определяется одним числом,
называют точечной.
Лекция №3, Статистическое моделирование,
Лакман И.А.
12

13. Свойства оценок

Полученные оценки должны быть достоверными, т.е. обладать
свойствами несмещенности, эффективности и состоятельности.
• Несмешанной называют статистическую оценку θ*, математическое
ожидание которой равно оценивающему параметру θ при любом
объеме выборки, т.е. М(θ*)= θ .
• Эффективной оценкой называют статистическую оценку θ*, которая
при заданном объеме выборки n имеет наименьшую возможную
дисперсию.
• Состоятельной называют статистическую оценку, которая при n→ ∞
и стремится по вероятности к оцениваемому параметру, т.е.:
lim P ( *) .
n
Лекция №3, Статистическое
моделирование, Лакман И.А.
13

14. Метод моментов для точечной оценки параметра распределения

Оценка одного параметра
Вид плотности распределения f(x, θ).
Требуется найти точечную оценку ˆ .
Для оценки одного параметра достаточно
относительного этого параметра.
Пусть M ( x ) xв
Тогда M ( x )
x f ( x, )dx ( )
одного
уравнения,
( ) xв
Решив уравнение
относительно параметра θ , найдем точечную оценку ˆ
Следовательно оценка есть функция от вариант выборки:
ˆ ( x1 , x2 ,..., xn )
Лекция №3, Статистическое
моделирование, Лакман И.А.
14

15. Метод моментов для точечной оценки параметра распределения

Оценка двух параметров
Вид плотности распределения f(x, θ1, θ2).
Требуется найти точечные оценки ˆ и ˆ
1
2
Для оценки двух параметров достаточно системы двух уравнений,
относительного этих параметров.
M ( x ) xв
Пусть
D( x ) Dв
Тогда M ( x ) x f ( x, 1 , 2 )dx 1 ( 1 )
D( x ) M ( x 2 ) M ( x ) 2 ( )
2 2
Решив систему относительно параметров θ1, θ2 , найдем точечные оценки ˆ1 ˆ2
Следовательно оценки есть функции от вариант выборки:
ˆ1 1( x1 , x2 ,..., xn )
ˆ2 2 ( x1 , x2 ,..., xn )
Лекция №3, Статистическое
моделирование, Лакман И.А.
15

16. Метод максимального правдоподобия

Для дискретных случайных величин.
Пусть Х дискретная случайная величина, которая принимает возможные
значения х1, х2,…,хп. Пусть закон распределения задан, но неизвестен
параметр распределения θ . Требуется найти точечную оценку ˆ .
Вероятность того, что величина Х , примет значение хi , р(хi , θ).
Определение: Функцией правдоподобия дискретной случайной величины
Х называют функцию аргумента θ
n
L( x1 , x2 ,..., xn ; ) p( x1; ) p( x2 ; ) ... p( xn ; ) П p( xi ; )
i 1
Где х1, х2,…,хп. – фиксированные числа.
Определение: Логарифмической функцией правдоподобия дискретной
случайной величины Х называют функцию аргумента θ
n
l ln L( x1 , x2 ,..., xn ; ) p( xi ; )
i 1
Лекция №3, Статистическое
моделирование, Лакман И.А.
16

17. Метод максимального правдоподобия

Определение: Оценкой максимального правдоподобия называют такую
оценку ˆ , для которой функция правдоподобия достигает максимума.
ˆ max L( x1, x2 ,..., xn ; ) max l ( x1, x2 ,..., xn ; )
i 1
i 1
Для ее нахождения решают
правдоподобия: d ln L
0
d
уравнение,
называемое
уравнением
2
d
ln L
ˆ
ˆ
Если при θ= ,
0 , то - точка максимума.
d 2
Лекция №3, Статистическое
моделирование, Лакман И.А.
17

18. Метод максимального правдоподобия

Для непрерывных случайных величин.
Пусть Х непрерывная случайная величина, которая пв результате
испытания приняла значения х1, х2,…,хп. Пусть вид плотности
распределения f(x) известен, но неизвестен параметр распределения θ.
Требуется найти точечную оценку ˆ .
Определение: Функцией правдоподобия непрерывной
величины Х называют функцию аргумента θ:
случайной
n
L( x1, x2 ,..., xn ; ) f ( x1; ) f ( x2 ; ) ... f ( xn ; ) П f ( xi ; )
Где х1, х2,…,хп. – фиксированные числа.
i 1
Оценку максимального правдоподобия неизвестного параметра
распределения непрерывной случайной величины ищут также, как и в
случае с дискретной случайной величины.
Лекция №3, Статистическое
моделирование, Лакман И.А.
18

19. Метод максимального правдоподобия

Для непрерывных случайных величин.
Если плотность распределения f(x) непрерывной случайной величины Х
определяется двумя неизвестными параметрами θ1, θ2, то функция
правдоподобия является функцией двух аргументов θ1, θ2 :
n
L( x1 , x2 ,..., xn ; 1 , 2 ) f ( x1; 1 , 2 ) f ( x2 ; 1 , 2 ) ... f ( xn ; 1 , 2 ) П f ( xi ; 1 , 2 )
Где х1, х2,…,хп. – фиксированные числа.
i 1
Для нахождения параметров θ1, θ2 решают систему уравнений:
ln L
0,
ln1L
0.
2
Лекция №3, Статистическое
моделирование, Лакман И.А.
19

20. Статистическая задача оценивания

Задача: по наблюдениям х1, х2,…,хп над случайной величиной Х,
распределенной равномерно на отрезке [0, a], оценить неизвестный
параметр а.
Сравним три способа оценивания:
1.
2 n
ˆ
Метод моментов a1 n xi
i 1
2.
Метод максимального правдоподобия aˆ 2
3.
Метод порядковых статистик
Где
xˆ 0,5
x( k ) x( k 1)
n 1
max xi
n
i
aˆ3 2 xˆ0,5 x( k ) x( k 1)
- выборочная квантиль порядка 0,5, т.е.
2
выборочная медиана, х(k) - член вариационного ряда с номером k.
(причем n=2k).
Лекция №3, Статистическое
моделирование, Лакман И.А.
20

21. Теоретическое сравнение оценок

1.
Все оценки aˆ1 , aˆ 2 , aˆ 3 являются несмещенными, их математические
ожидания равны истинным параметрам а. (доказать сам-но)
2.
Дисперсии оценок: (будет доказано на лекции)
2 n a2
Daˆ1 D xi
n i 1 n
a2
n 1
Daˆ 2 D
max xi
i
n
n( n 2)
a2
Daˆ3 D x( k ) x( k 1)
n
3.
Наименьшую дисперсию имеет третья оценка
Примечание: Для получения значения дисперсии для третьей оценки использовали:
Теорема Крамера: Выборочная р-квантиль имеет дисперсию приближенно равную
1 p(1 p )
n f 2 ( x p ) , где хр – истинная р-квантиль, f(x) – плотность
распределения наблюдений выборки.
Лекция №3, Статистическое
моделирование, Лакман И.А.
21

22. Статистическое сравнение оценок

1.
Значение оценок концентрируются в окрестности оцениваемого
параметра (свойство несмещенности).
2.
С ростом числа наблюдений в выборке точность (величина разброса)
оценок улучшается (свойство несмещенности).
То есть размах R и стандартное отклонение S уменьшается.
R max ai min ai
3.
1 n
Sa
( ai a ) 2
n 1 i 1
1 n
a ai
n i 1
Различные оценки различаются по величине средней ошибки. Откуда
следует, что различные способы обработки наблюдений нужно
сравнивать по величине среднего значения некоторого критерия
качества, например среднего квадрата ошибки.
Лекция №3, Статистическое
моделирование, Лакман И.А.
22

23. Виды плотностей распределения основных распределений

Распределение Фишера с т и п степенями свободы
n m
m
n m
m
1
m 2
2 m 2
2
f ( x)
x
1 x
n
n m n
2 2
Распределение «Хи-квадрат» с п степенями свободы
1
f ( x)
2
n
2
n
2
x
n 1
2
e
x
2
Распределение Стьюдента с т степенями свободы
m 1
m 1
2
1
x 2 2
f ( x)
1
m
m m
2
Здесь 0 x , а Г – гамма-функция.
Лекция №3, Статистическое
моделирование, Лакман И.А.
23