Основные понятия математической статистики

1.

Дисциплина:
МАТЕМАТИКА ППИ
Лектор: Ахкамова Юлия Абдулловна
доцент кафедры математики и методики
обучения математике ЮУрГГПУ
[email protected]

2.

МАТЕМАТИКА ППИ
ЛЕКЦИЯ № 20.
Основные понятия
математической статистики

3. ЛИТЕРАТУРА

Шолохович Ф.А. Высшая
математика в кратком изложении.
Баврин И.И. Высшая математика.
Данко П.Е., Попов А.Г и др. Высшая
математика в упражнениях и
задачах, часть II.

4.

ЛИТЕРАТУРА
Гмурман В.Е.
Теория вероятностей
и математическая
статистика,
Высшее образование,
2009.

5.

ЛИТЕРАТУРА
Гмурман В.Е. Теория вероятностей и
математическая статистика, Высшее
образование,2006, с. 17-30.
Гмурман В.Е. Руководство к решению
задач по теории вероятностей и
математической статистике. М.:
Высшее образование. 2007.

6. Учебные вопросы

1.Выборочный метод. Выборка.
2. Вариационный ряд.
Графическое представление
вариационного ряда.
3.Основные числовые
характеристики вариационного
ряда. Примеры задач.

7.

4.Статистическая проверка гипотез
5.Корреляция.Коэффициент
. Основы регрессионного
корреляции
анализа

8. УЧЕБНЫЙ ВОПРОС.

Выборочный метод.
Выборка.

9.

Математическая статистика — наука о
математических методах анализа
данных полученных при проведении
массовых наблюдений (измерений
опытов).
В зависимости от математической природы
конкретных результатов наблюдений статистика
математическая делится на статистику чисел ,
многомерный статистический анализ функций
(процессов) и временных рядов, статистику
объектов нечисловой природы.

10.

Математическая статистика,
которая изучает методы сбора,
обработки и анализа данных,
получаемых в результате
наблюдений многократных
случайных явлений.

11.

К числу задач, решаемых методами
математической статистики, относятся:
изучение большой совокупности объектов
по небольшому их количеству,
извлеченному из совокупности случайным
образом (выборочный метод);
выяснение характера распределения,
нахождение приближенных значений
параметров распределения;
определение формы и силы связи между
случайными величинами.

12.

Генеральная совокупность — это общая
группа предметов, подлежащих
статистическому исследованию.
Она может быть большой, поэтому
физически невозможно исследовать всю
генеральную совокупность. К тому же
затраты на сбор данных во всей
генеральной совокупности очень высоки, да
и риск ошибки многократно возрастает.
Кроме того, наблюдение может быть
также связано с уничтожением
исследуемого образца (например, проверка
качества консервов).

13.

Пример привести.
Принимая во внимание все
вышеперечисленные причины, из
генеральной совокупности случайным
образом отбирается выборка —небольшое
количество предметов, после изучения
которой и делаются выводы о
генеральной совокупности.
При составлении выборки можно поступать
2-мя способами: после того, как объем
отобран и изучен, его можно возвращать в
генеральную совокупность, а можно не
возвращать.

14.

Пример привести.
Повторная выборка – это выборка, при
которой выбранный объект перед
отбором следующего возвращается в
генеральную совокупность,
а бесповторной выборкой называют
выборку при которой объект не
возвращается в совокупность.
На практике обычно пользуются
бесповторным случайным отбором.

15.

Для того, чтобы по данным выборки
можно было уверенно судить об
интересующем признаке, необходимо,
чтобы объекты выборки ее правильно
представили, т. е. выборка должна
правильно отображать объекты
генеральной совокупности. Если объем
генеральной совокупности большой, а
выборка невелика, то грань между
повторной и бесповторной выборкой
практически неразличима.

16.

В общем случае генеральную
совокупность считают бесконечной.
Пример повторной и бесповторной
выборки привести.

17. Опрос по учебному вопросу

В чем отличие подхода к решению
задач математической статистикой и
теорией вероятностей?
В чем отличие генеральной
совокупности от выборки?
Привести примеры повторной и
бесповторной выборки.

18. УЧЕБНЫЙ ВОПРОС

Вариационный ряд.
Графическое представление
вариационного ряда.

19.

20.

21.

22.

Статистическое распределение выборки удобно
представлять в форме таблицы распределения
частот,
называемой статистическим дискретным рядом
распределения:
(сумма всех частот равна объему выборки
∑ni=n)
...
n1
n2
...
nk

23.

или
в виде таблицы распределения относительных частот:
(сумма всех относительных частот равна единице
∑рi*=1)
...
р1*
р2*
...
рm*

24.

Пример . При измерениях в однородных группах
обследуемых получены следующие выборки:
71, 72, 74, 70, 70, 72, 71, 74, 71, 72, 71, 73, 72, 72,
72, 74, 72, 73, 72, 74 (частота пульса).
Составить по этим результатам статистический
ряд распределения
частот и относительных частот.
Решение. 1) Статистический ряд распределения
частот:
ni
70
71
72
73
74
2
4
8
2
4

25.

2) Объем выборки: n=2+4+8+2+4=20.
Найдем относительные частоты, для чего
разделим частоты на
объем выборки ni /n =рi*:
2/20=0.1; 4/20=0.2; 0.4; 4/20=0.2;
2/20=0.1. Напишем распределение относительных
частот:
Контроль: 0,1+0,2+0,4+0,2+0,1=1.
р i*
70
71
72
73
74
0.1
0.2
0.4
0.2
0.1

26.

2) Объем выборки: n=2+4+8+2+4=20.
Найдем относительные частоты, для чего
разделим частоты на
объем выборки ni /n =рi*:
2/20=0.1; 4/20=0.2; 0.4; 4/20=0.2;
2/20=0.1. Напишем распределение относительных
частот:
Контроль: 0,1+0,2+0,4+0,2+0,1=1.
р i*
70
71
72
73
74
0.1
0.2
0.4
0.2
0.1

27.

28.

Пример. Постройте полигон частот и
относительных частот по данным
предыдущего примера.
Решение:
Используя дискретный статистический
ряд распределения, составленный в
примере 1 построим полигон частот и
полигон относительных частот р i*

29.

30.

Если
же интересующий нас
признак генеральной
совокупности Х распределен
непрерывно или его
дискретность учитывать
нецелесообразно ( или
невозможно), то варианты
группируются в интервалы.

31.

32.

33.

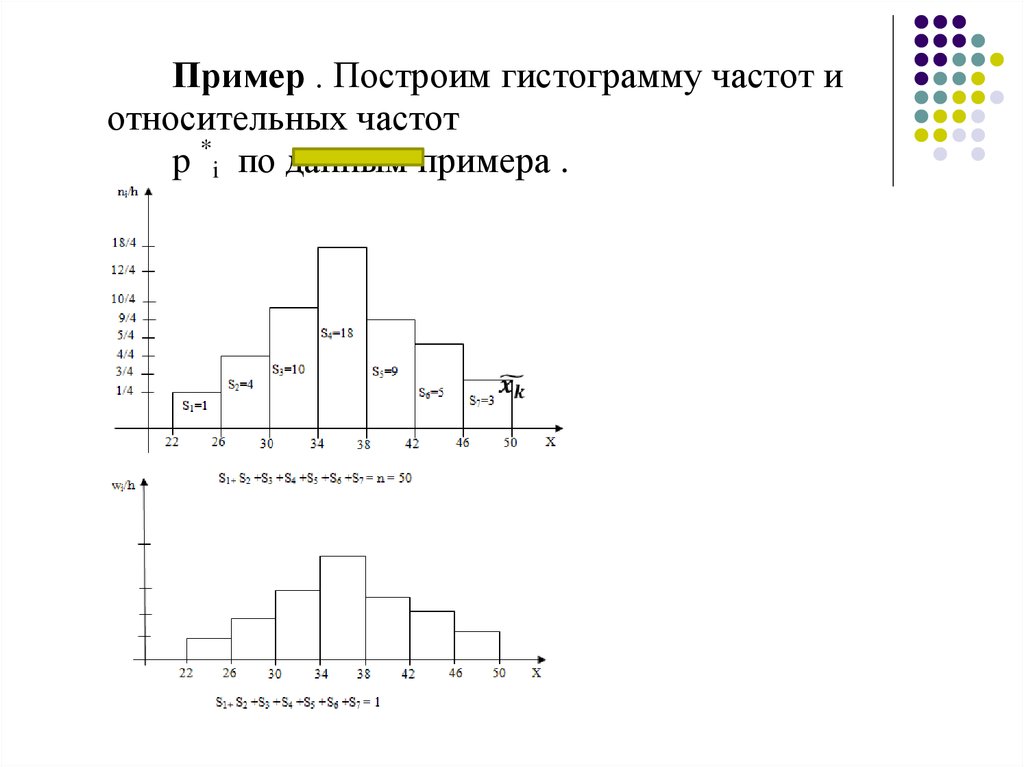
Пример . Построим гистограмму частот и
относительных частот
p *i по данным примера .

34. Опрос по учебному вопросу

35. УЧЕБНЫЙ ВОПРОС.

Основные числовые
характеристики
вариационного ряда.
Примеры задач.

36.

37.

Пусть
из генеральной
совокупности в результате
независимых наблюдений
над количественным
признаком извлечена
выборка объема n со
значениями
признака x1,x2,x3,…,xk.

38.

39.

40.

41.

42.

43. ПРИМЕР

Рост
134137
137140
140143
143146
146149
149152
152155
155158
158161
161164
164167
167170
170173
Число
женщин
1
4
16
53
121
193
229
186
121
53
71
5
1

44.

рi*
70
71
72
73
74
0.1
0.2
0.4
0.2
0.1

45.

46. Опрос по учебному вопросу

Дать определение выборочной
средней. Ее обозначение, формула по
определению?
Дать определение выборочной
среднеквадратического отклонения. Ее
обозначение, формула по
определению?

47.

Учебный вопрос
Статистическая проверка
гипотез

48. подвопросы

1. Понятие о точечных и
интервальных оценках. Виды
статистических оценок параметров
распределения (несмещенная,
эффективная и т.п.).
2.Основные понятия статистической
проверки гипотез.
3. Критерий χ-квадрат. Примеры
задач.

49. ПОДВОПРОС

Понятие о точечных и
интервальных оценках. Виды
статистических оценок
параметров распределения

50.

51.

Использование статистической оценки,
математическое ожидание которой не
равно оцениваемому параметру,
приводит к систематическим ошибкам.
Соблюдение требования устраняет
систематические ошибки.
Несмещенной оценкой называют
статистическую оценку , математическое
ожидание которой равно оцениваемому
параметру.

52.