Similar presentations:
Неопределённый интеграл
1. Неопределённый интеграл.
2. Первообразная.
Задача дифференциального исчисления: поданной функции найти её производную.
Задача интегрального исчисления:
функцию, зная её производную.
найти
• Функция F(x) называется первообразной для
функции f(x) на заданном промежутке, если
для любого х из этого промежутка справедливо
равенство Fʹ(x)=f(x).
3. Пример 1. Найти первообразные для функций:
1)f ( x) 3 x
2)
f ( x) x
3)
1
f ( x)
x
1
f ( x) ,
x
1
f ( x) ,
x
2
5
F ( x) x
3
x R,
x 3x
3
2
1 6
F ( x) x
6
1 6
x R, x x 5
6
F ( x) ln x
x R \ 0
x 0;
x ; 0
1
F ( x) ln x, ln x
x
1
1
F ( x) ln( x), ln( x)
1
x
x
4.
Для всякой ли функции f(x) существуетпервообразная?
Теорема.
Если функция непрерывна на какомнибудь промежутке, то она имеет на
нём первообразную.
5.
Найти первообразную для функции f(x)=4x3.F3 ( x) x 4 3
F2 ( x) x 5
4
F1 ( x) x 4
F ( x) x 4 C
f ( x) 4 x
3
Т.о. функция f(x)=4x3, х∈R имеет бесконечное множество
первообразных.
6.
Теорема.Если функция F(x) является первообразной для
функции f(x) на некотором промежутке, то
множество всех первообразных этой функции
имеет вид F(x)+C, где C∈R.
y
Геометрически:
F(x)+C представляет собой
семейство
кривых,
получаемых из каждой из них
параллельным
переносом
вдоль оси ОУ.
С
0
интегральная кривая
x
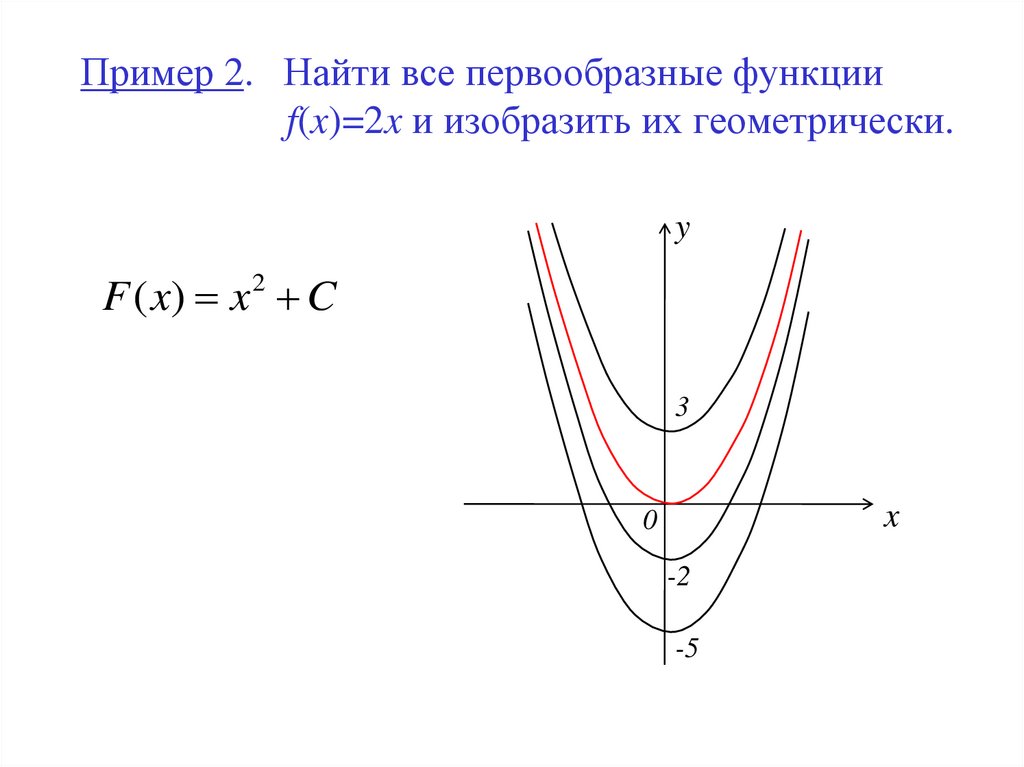
7. Пример 2. Найти все первообразные функции f(x)=2x и изобразить их геометрически.
yF ( x) x 2 C
3
x
0
-2
-5
8. Неопределённый интеграл.
Множество всех первообразных F(x)+C
функции f(x) на некотором промежутке
называется неопределённым интегралом и
обозначается символом f ( x)dx , т.е
f ( x) dx F ( x) C
9.
f ( x) dx F ( x) Cf (x ) - подынтегральная функция
f ( x) dx - подынтегральное выражение
х – переменная интегрирования
- знак неопределённого интеграла
F(x)+C – множество всех первообразных
С – постоянная интегрирования
Процесс нахождения первообразной функции называется
интегрированием, а раздел математики- интегральным
исчислением.
10. Свойства неопределённого интеграла.
• 10. Дифференциал от неопределённогоинтеграла
равен
подынтегральному
выражению, а производная неопределённого
интеграла равна подынтегральной функции:
d f ( x) dx f ( x) dx,
f ( x) dx f ( x)
11.
Доказательство:d f ( x) dx d F ( x) C d F ( x) d C F ( x) dx f ( x) dx
f ( x) dx ( F ( x) C ) F ( x) C f ( x)
То есть правильность
дифференцированием.
Равенство
интегрирования
проверяется
3x 4 dx x 4 x C верно, так как
2
3
x 4x C 3x 4
3
2
12.
• 20.Неопределённый
интеграл
от
дифференциала некоторой функции равен этой
функции плюс произвольная постоянная, т.е
d F ( x) F ( x) C
Доказательство.
d
F
(
x
)
F
x dx f ( x) dx F x C
13.
• 30.Неопределённый
интеграл
от
алгебраической суммы двух или нескольких
функций равен алгебраической сумме их
интегралов, т.е
f ( x) g ( x) dx f ( x) dx g ( x) dx
Доказательство:
воспользуемся свойством 10.
f ( x) g ( x) dx f ( x) g ( x)
f ( x) dx g ( x) dx f ( x) dx g ( x) dx f ( x) g ( x)
14.
• 40. Постоянный множитель можно выносить зазнак интеграла, т.е
a f ( x) dx a f ( x) dx , a 0
Доказательство: воспользуемся свойством 10:
a f ( x) dx a f ( x)
a f ( x) dx a f ( x) dx a f ( x)
15. Таблица интегралов.
1)0dx C, C const
n 1
x
2) x n dx
C , n 1
n 1
В частности:
dx x C
dx
3)
ln x C
x
ax
4) a dx
C , a 0, a 1
ln a
x
5)
cos xdx sin x C
6)
sin xdx cos x C
x
x
e
dx
e
C
В частности:
16.
7)dx
cos 2 x tan x C
9)
dx
1
x
arctan
C, a 0
a2 x2 a
a
8)
В частности:
10)
dx
a x
2
2
arcsin
dx
sin 2 x cot x C
dx
1 x 2 arctan x C
x
C, a 0
a
В частности:
dx
1 x arcsin x C
2
11)
12)
dx
1
x a
ln
x 2 a 2 2a x a C
dx
x a
2
2
a 0
ln x x 2 a 2 C
17. Основные методы интегрирования.
Метод непосредственного интегрирования.Непосредственным интегрированием называется
такой метод вычисления интегралов, при котором
они сводятся к табличным путём применения к ним
основных свойств неопределённого интеграла. При
этом
подынтегральную
функцию
обычно
соответствующим образом преобразуют.
18. Пример 3. Вычислить интеграл
2 x 4 3 sin x 5e x dx2 x 3sin x 5e dx 2 x dx 3sin x dx 5e dx
4
x
4
x
4 1
x
2 x 4 dx 3 sin x dx 5 e x dx 2
C1 3 cos x C2 5 e x C3
4 1
2 5
x 3 cos x 5e x C ,
5
C C1 C 2 C3
19. Пример 4. Вычислить интеграл
2x xdx
Пример 4. Вычислить интеграл 3
x
2x x
3
6
2
dx
2
x
x
x
dx
2
x
3x
dx
1
13
6
1
7
x
12 6 13
12 2 6
2
C x C x x C
13
13
13
6
20. Пример 5. Вычислить интеграл
2 x4x dx
2 x4
2 x4
2
3
dx
dx
dx
x
x
x x x dx
4
dx
x
2 x 3 dx 2 ln x C
x
4
21. Пример 6. Вычислить интеграл
x2x
3
4
dx
x
48
x
2x
x
x
x
3
4
dx
3
16
dx
48
dx ln 48 C
22. Пример 7. Вычислить интеграл
dxПример 7. Вычислить интеграл 2
sin x cos 2 x
dx
1
sin 2 x cos 2 x
sin 2 x cos 2 x sin 2 x cos 2 x dx sin 2 x cos 2 x dx
sin 2 x
cos 2 x
1
1
dx
2
dx
2
2
2
2
2
cos x sin x
sin x cos x sin x cos x
dx
dx
2 tan x cot x C
2
cos x
sin x
23. Пример 8. Вычислить интеграл
dx25 4 x 2
dx
25 4 x 2
dx
1
dx
2
4 5
25
2
2
4 x
x
4
2
1 2
2x
1
2x
arctan
C arctan
C
4 5
5
10
5
24. Пример 9. Вычислить интеграл
x2x 2 1 dx
x2 1
x2
x2 1 1
1
x 2 1 dx x 2 1 dx x 2 1 x 2 1 dx
1
dx
1 2
x arctan x C
dx dx 2
x 1
x 1
25. Пример 10. Вычислить интеграл
2cot
x dx
2
2
2
cos
x
1
sin
x
1
sin
x
2
cot x dx sin 2 x dx sin 2 x dx sin 2 x sin 2 x dx
dx
1
2 1 dx 2 dx cot x x C
sin x
sin x
26. Пример 11. Вычислить интеграл
x 3 3x 2 3x 1Пример 11. Вычислить интеграл
dx
2
x x
x 3 3x 2 3x 1
x 3 1 3 x x 1
dx
dx
2
x x
x x 1
x 1 x 2 x 1 3 x x 1
x 1 x 2 2 x 1
dx
dx
x x 1
x x 1
x2 2x 1
x2 2x 1
dx
dx
dx x dx 2 dx
x
x x
x
x
x2
2 x ln x C
2
27. Пример 12. Вычислить интеграл
1 2x2x 2 1 x 2 dx
1 x2
1 2x2
1 x2 x2
x2
x 2 1 x 2 dx x 2 1 x 2 dx x 2 1 x 2 x 2 1 x 2 dx
1
dx
dx
dx
1
2
2
dx 2
x dx
2
2
2
x
1 x
1 x
x 1 x
x 1
1
arctan x C arctan x C
1
x


























 mathematics
mathematics








