Урок №3. Тема 1. Аксиомы стереометрии и их следствия

1.

Урок №3
Тема 1. Аксиомы
стереометрии и их
следствия.

2. Цели обучения:

• 10.2.1 - знать аксиомы стереометрии, их
следствия; иллюстрировать и записывать их
с помощью математических символов;

3. Геометрия

Планиметрия
Стереометрия
stereos
телесный, твердый,
объемный,
пространственный

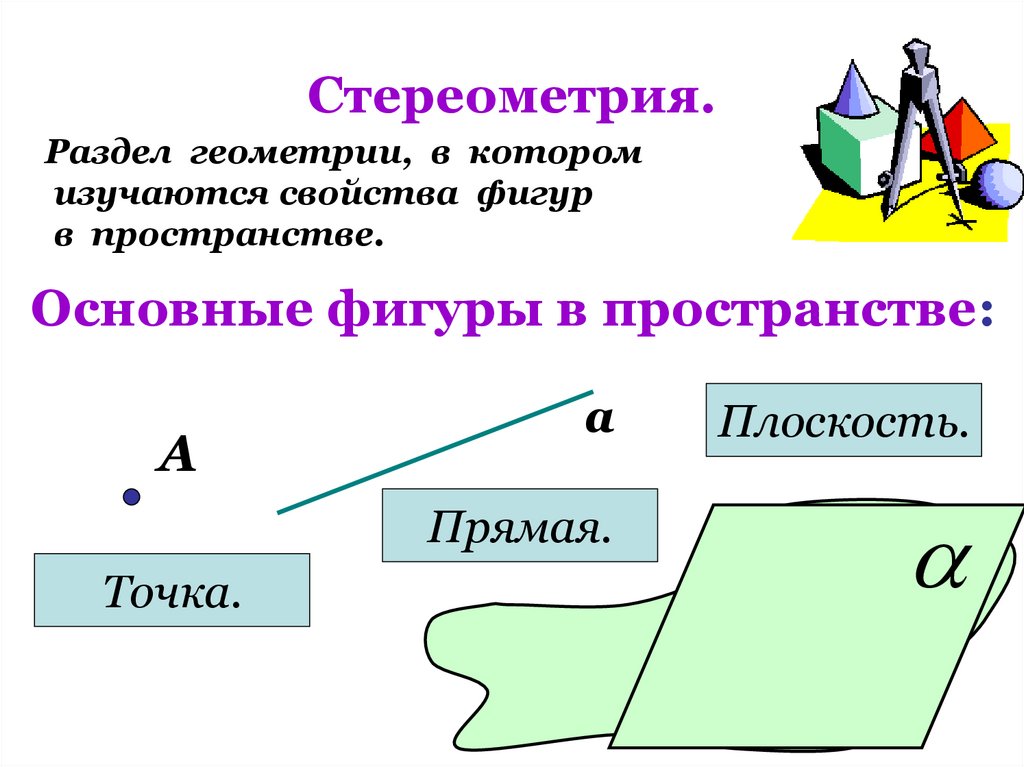
4. Стереометрия.

Раздел геометрии, в котором
изучаются свойства фигур
в пространстве.
Основные фигуры в пространстве:
А
Точка.
а
Плоскость.
Прямая.

5.

A, B, C, …
a, b, c, …
или
AВ, BС, CD, …
, , ,

6.

7. Аксиома

(от греч. axíõma – принятие положения)
исходное положение
научной теории,
принимаемое без
доказательства

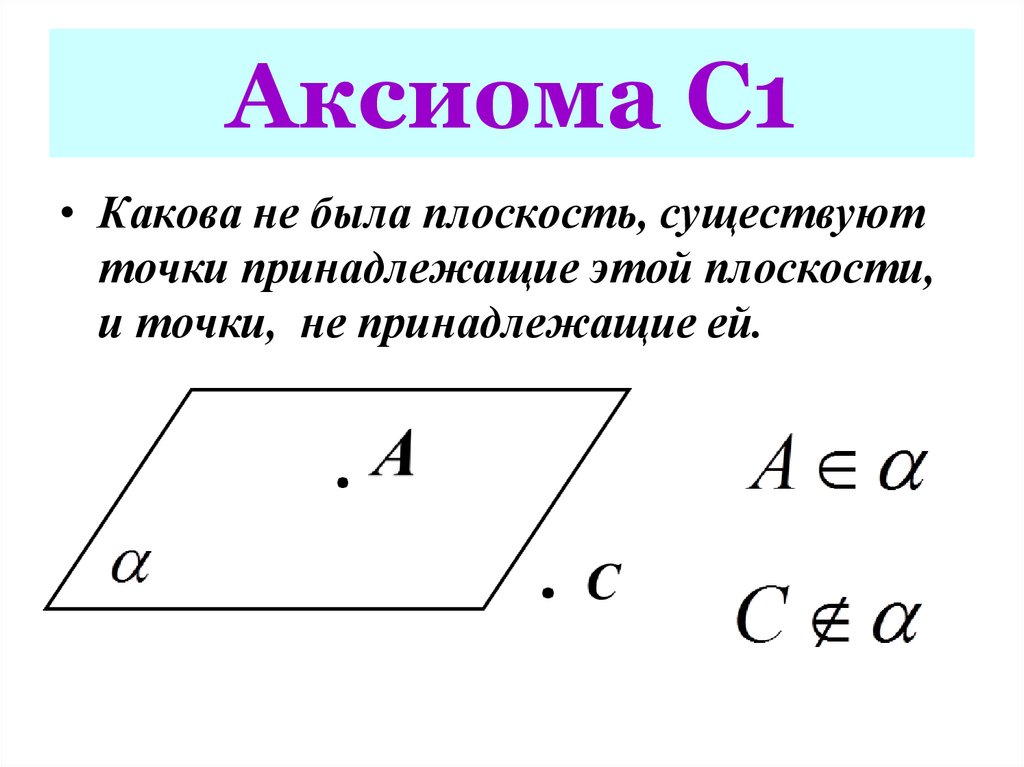
8. Аксиома С1

• Какова не была плоскость, существуют
точки принадлежащие этой плоскости,
и точки, не принадлежащие ей.

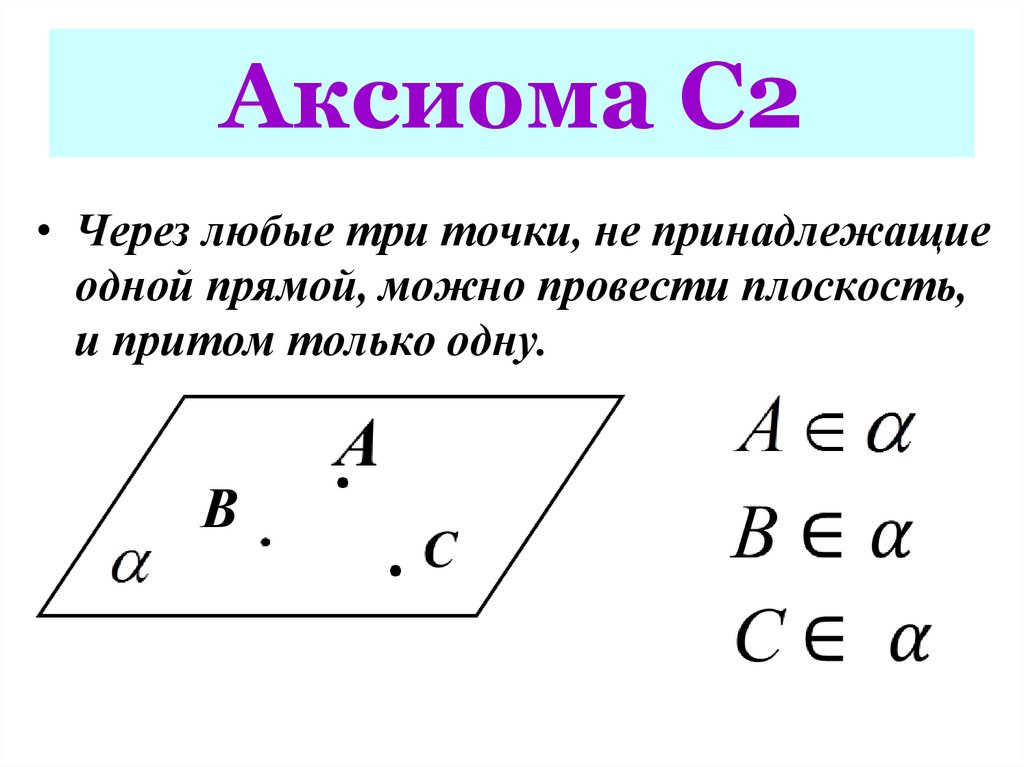
9. Аксиома С2

• Через любые три точки, не принадлежащие
одной прямой, можно провести плоскость,
и притом только одну.
В

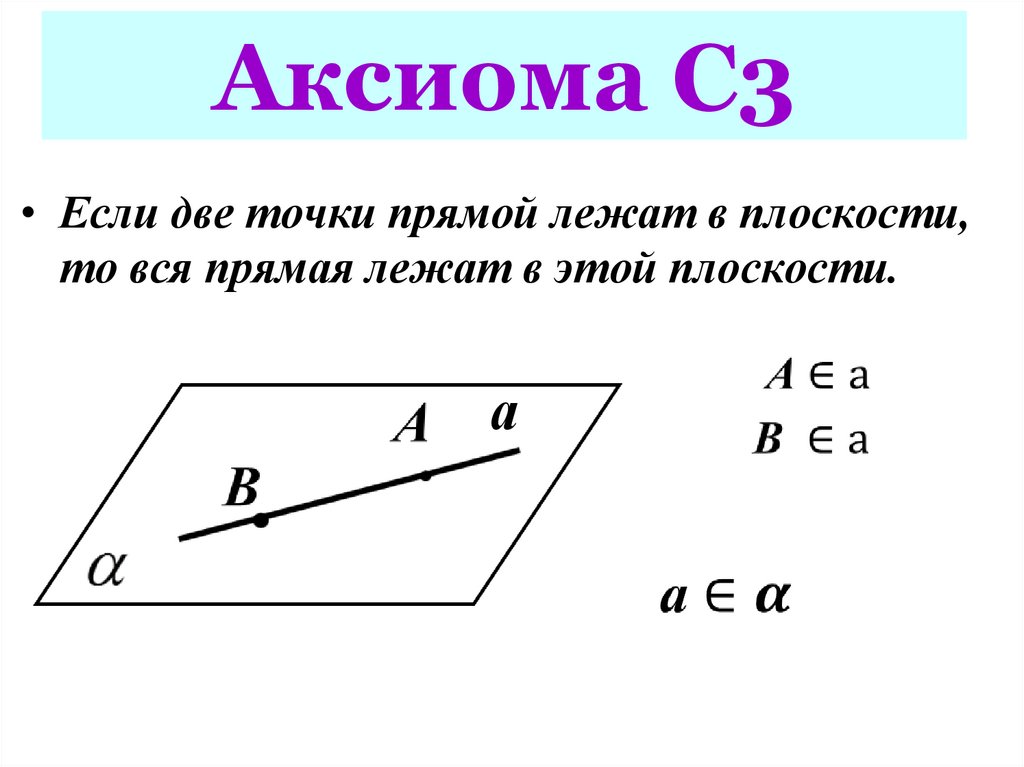
10. Аксиома С3

• Если две точки прямой лежат в плоскости,
то вся прямая лежат в этой плоскости.
а

11.

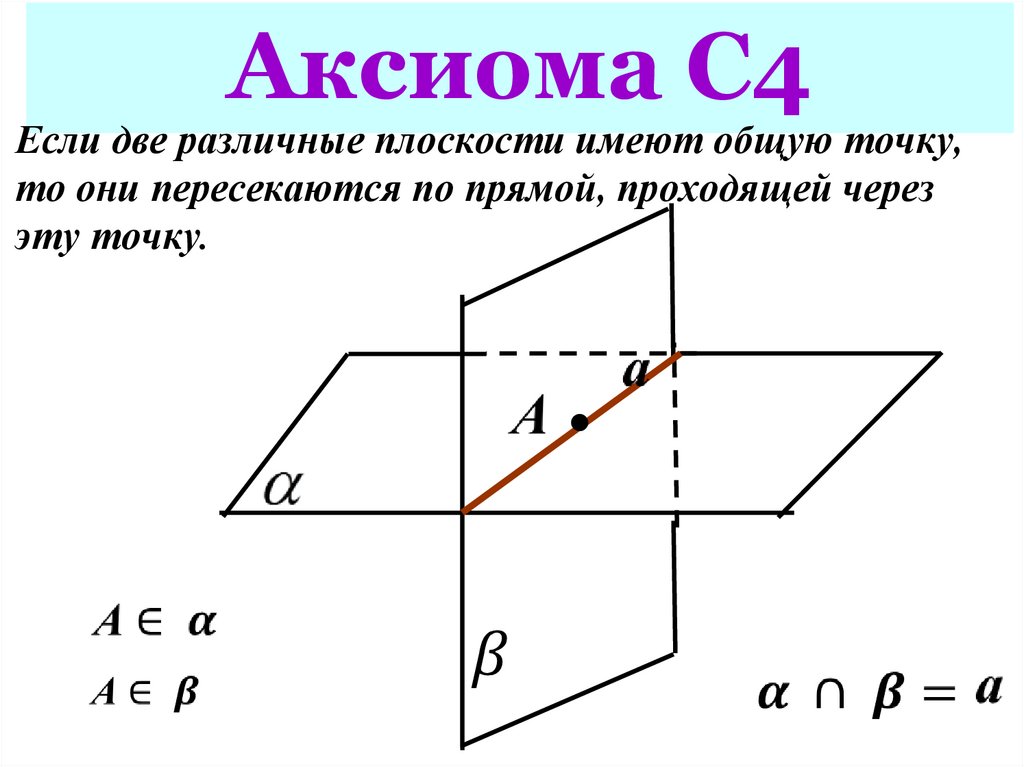
Аксиома С4
Если две различные плоскости имеют общую точку,
то они пересекаются по прямой, проходящей через
эту точку.

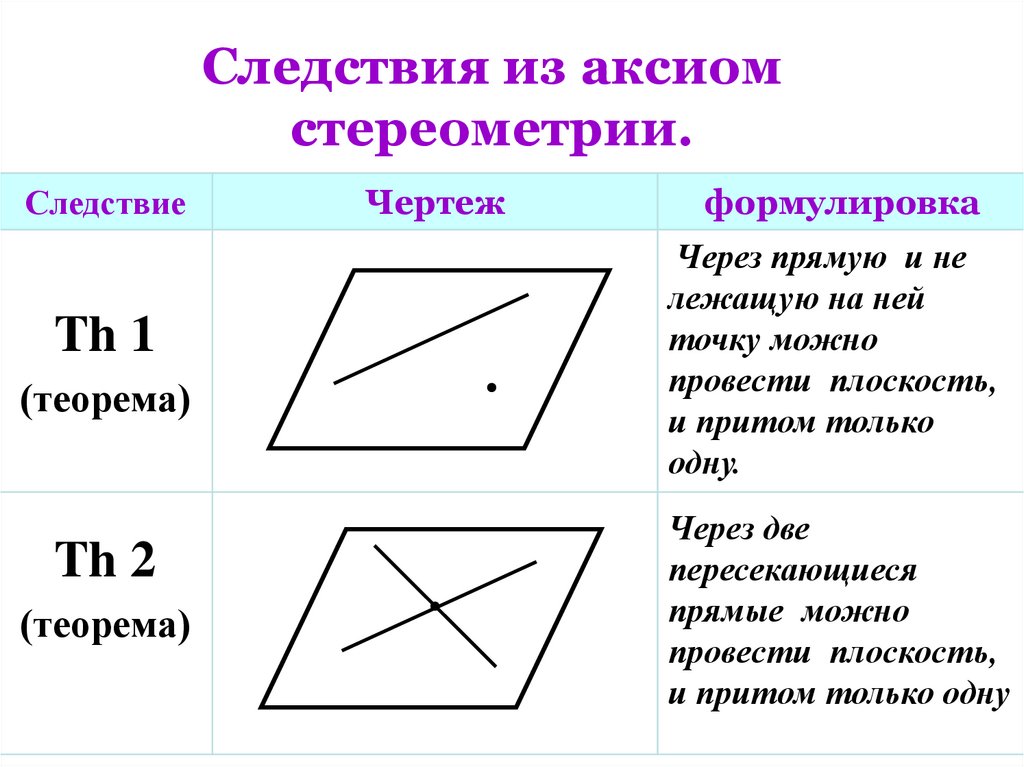
12. Следствия из аксиом стереометрии.

Следствие
Th 1
(теорема)
Th 2
(теорема)
Чертеж
формулировка
Через прямую и не
лежащую на ней
точку можно
провести плоскость,
и притом только
одну.
Через две
пересекающиеся
прямые можно
провести плоскость,
и притом только одну

13.

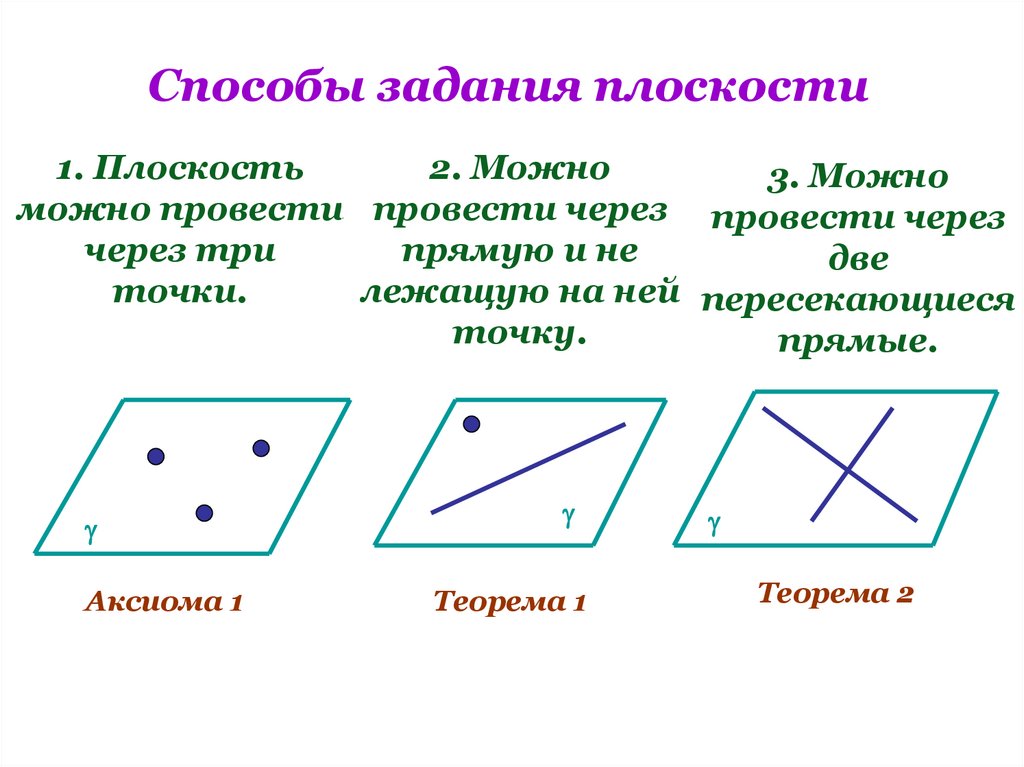
Способы задания плоскости
1. Плоскость
2. Можно
3. Можно
можно провести провести через провести через
через три
прямую и не
две
точки.
лежащую на ней пересекающиеся
точку.
прямые.
Аксиома 1
Теорема 1
Теорема 2

14. Рефлексия