Аксиомы стереометрии и простейшие следствия из них

1. Аксиомы стереометрии и простейшие следствия из них

2. Историческая справка

3.

ПЛАНИМЕТРИЯ СТЕРЕОМЕТРИЯ
Изучает свойства
геометрических фигур
на плоскости
Изучает свойства фигур
в пространстве
В переводе с греческого
слово «геометрия»
означает «землемерие»
«гео» – по-гречески
земля, «метрео» –
мерить
Слово «стереометрия»
происходит от
греческих слов
«стереос» объемный,
пространственный,
«метрео» – мерить

4.

ПЛАНИМЕТРИЯ СТЕРЕОМЕТРИЯ
Основные фигуры: точка,
прямая
Основные фигуры: точка,
прямая, плоскость
Другие фигуры: отрезок,
луч, треугольник, квадрат,
ромб, параллелограмм,
трапеция, прямоугольник,
выпуклые и невыпуклые nугольники, круг,
окружность, дуга и др.
Наряду с этими фигурами
мы будем рассматривать
геометрические тела и их
поверхности.
Например, многогранники.
Куб, параллелепипед,
призма, пирамида.
Тела вращения.
Шар, сфера, цилиндр,
конус.

5.

Для обозначения точек как и в планиметрии
используют прописные латинские буквы:
F
A
D
Прямую обозначают одной строчной
латинской буквой или двумя прописными
латинскими буквами:
l
A
B

6.

Плоскость в стереометрии обозначают
греческими буквами, например:
А на рисунках чаще всего плоскость
изображают в виде параллелограмма. Но
следует понимать и представлять себе
данную геометрическую фигуру как
неограниченную во все стороны.

7.

Изучая свойства геометрических фигур –
воображаемых объектов, мы получаем
представление о геометрических свойствах
реальных предметов (их форме, взаимном
расположении и т. д.) и можем использовать эти
свойства в практической деятельности. В этом
состоит прикладное значение геометрии.
Геометрия, в частности стереометрия, широко
используется в строительном деле, архитектуре,
машиностроении, геодезии, во многих
других областях науки и техники.

8.

Аксиома – это утверждение о свойствах
геометрических фигур, принимается в
качестве исходных положений, на основе
которых доказываются далее теоремы и
вообще строится вся геометрия.
Аксиомы планиметрии:
- через любые две точки можно провести прямую и
притом только одну.
-из трех точек прямой одна, и только одна, лежит
между двумя другими.
-имеются по крайней мере три точки, не лежащие
на одной прямой…

9.

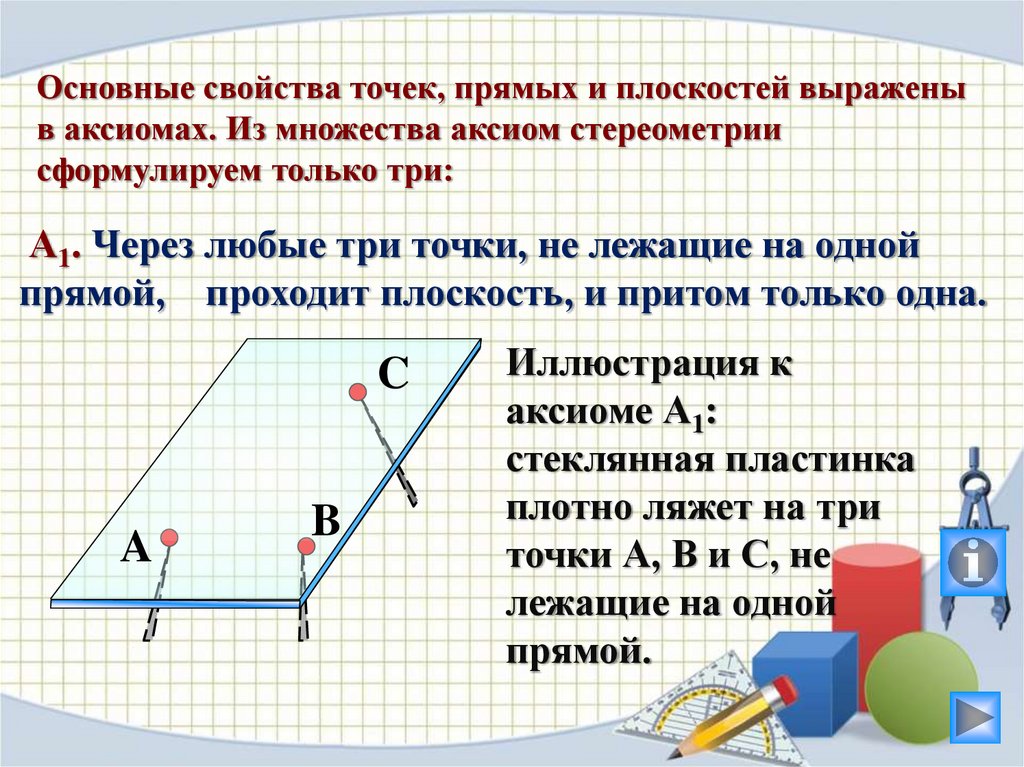
Основные свойства точек, прямых и плоскостей выражены
в аксиомах. Из множества аксиом стереометрии
сформулируем только три:
А1. Через любые три точки, не лежащие на одной
прямой, проходит плоскость, и притом только одна.
C
A
B
Иллюстрация к
аксиоме А1:
стеклянная пластинка
плотно ляжет на три
точки А, В и С, не
лежащие на одной
прямой.

10.

Самый простой пример к аксиоме А1 из
повседневной жизни:
Табурет с тремя ножками всегда идеально
встанет на пол и не будет качаться. У
табурета с четырьмя ножками бывают
проблемы с устойчивостью, если ножки стула
не одинаковые по длине.
Табурет качается, т. е. опирается на три
ножки, а четвертая ножка (четвертая
«точка») не лежит в плоскости
пола, а висит в воздухе.

11.

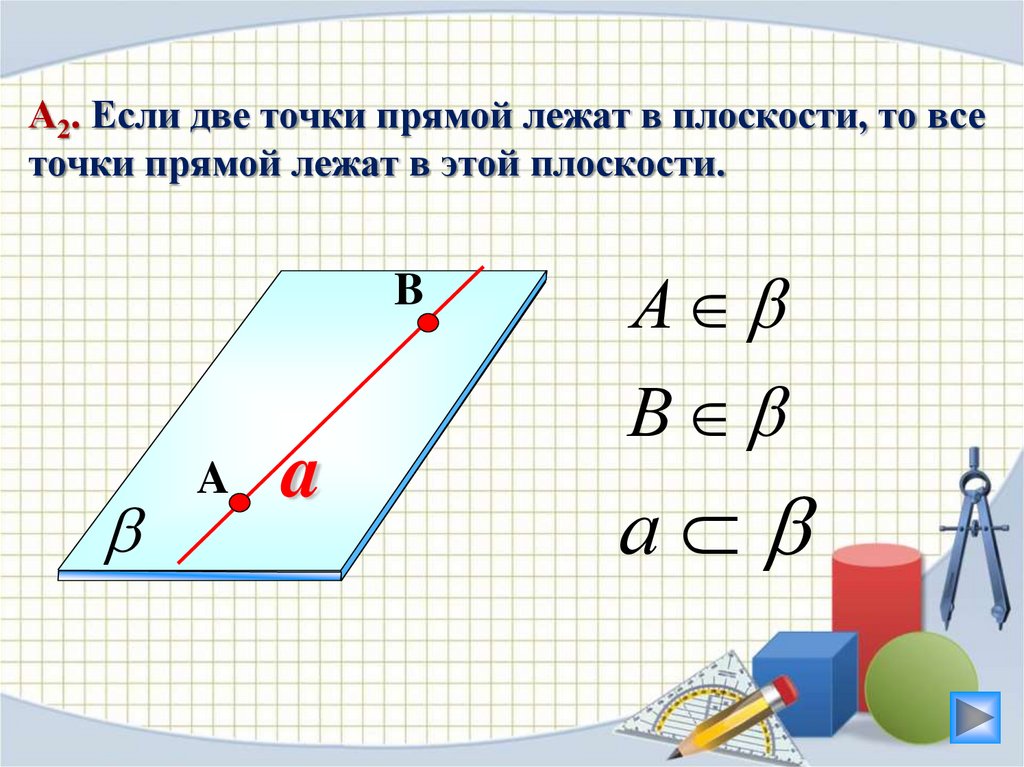
А2. Если две точки прямой лежат в плоскости, то все
точки прямой лежат в этой плоскости.
B
A
a
А
В
а

12.

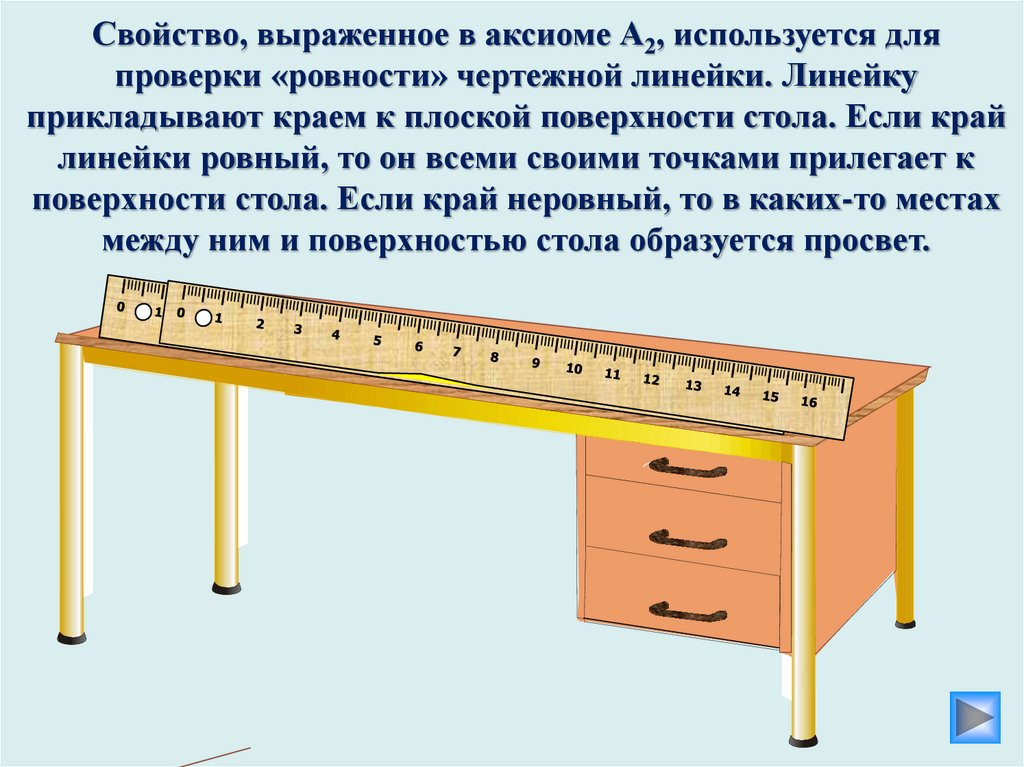
Свойство, выраженное в аксиоме А2, используется для
проверки «ровности» чертежной линейки. Линейку
прикладывают краем к плоской поверхности стола. Если край
линейки ровный, то он всеми своими точками прилегает к
поверхности стола. Если край неровный, то в каких-то местах
между ним и поверхностью стола образуется просвет.

13.

А3. Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие
точки этих плоскостей.
Самый простой пример
к аксиоме А3 из
повседневной жизни
является пересечение
двух смежных стен
комнаты.
a
a

14.

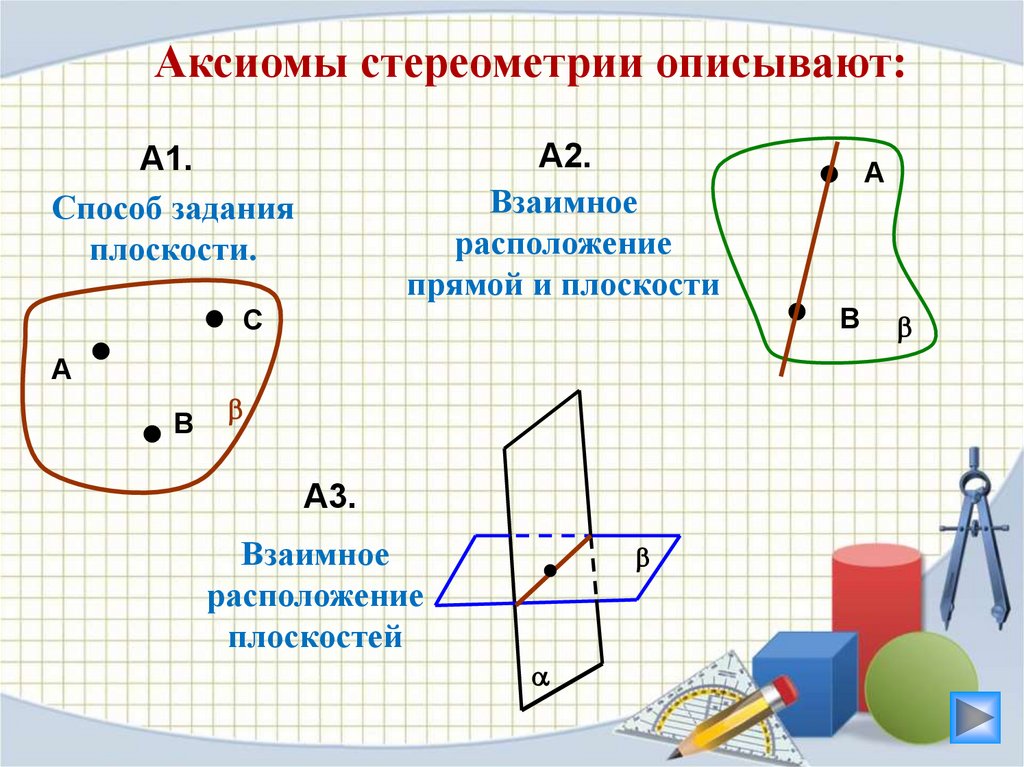
Аксиомы стереометрии описывают:
А2.
Взаимное
расположение
прямой и плоскости
А1.
Способ задания
плоскости.
В
С
А
В
А
А3.
Взаимное
расположение
плоскостей

15.

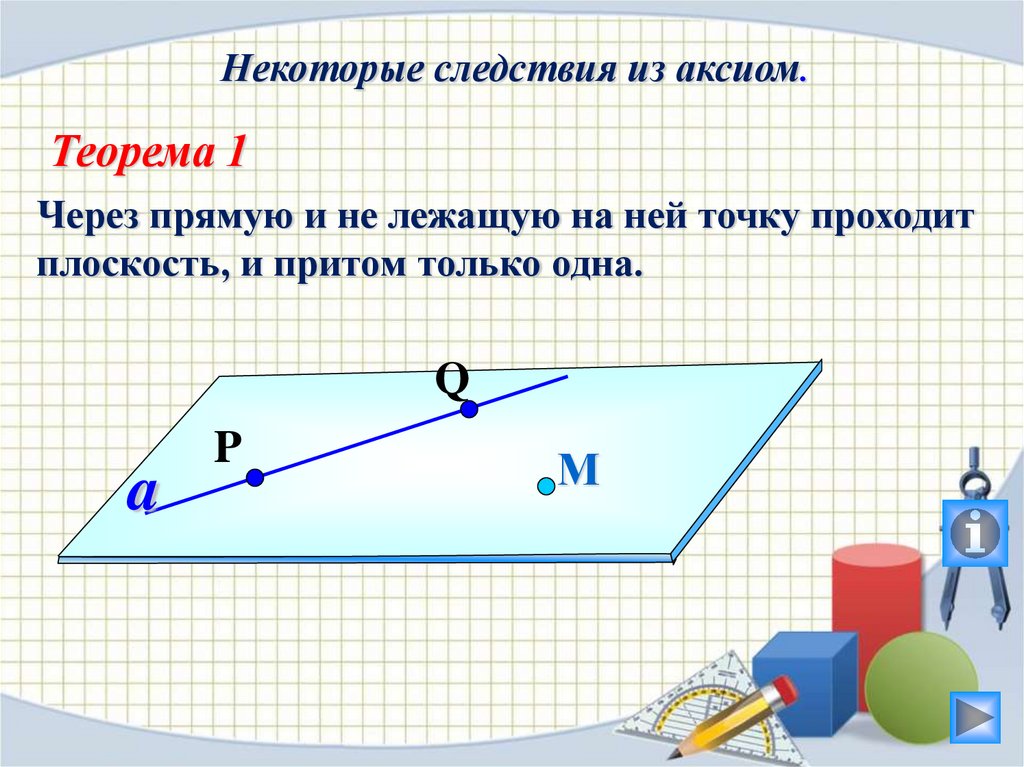
Некоторые следствия из аксиом.
Теорема 1
Через прямую и не лежащую на ней точку проходит
плоскость, и притом только одна.
Q
a
P
М

16.

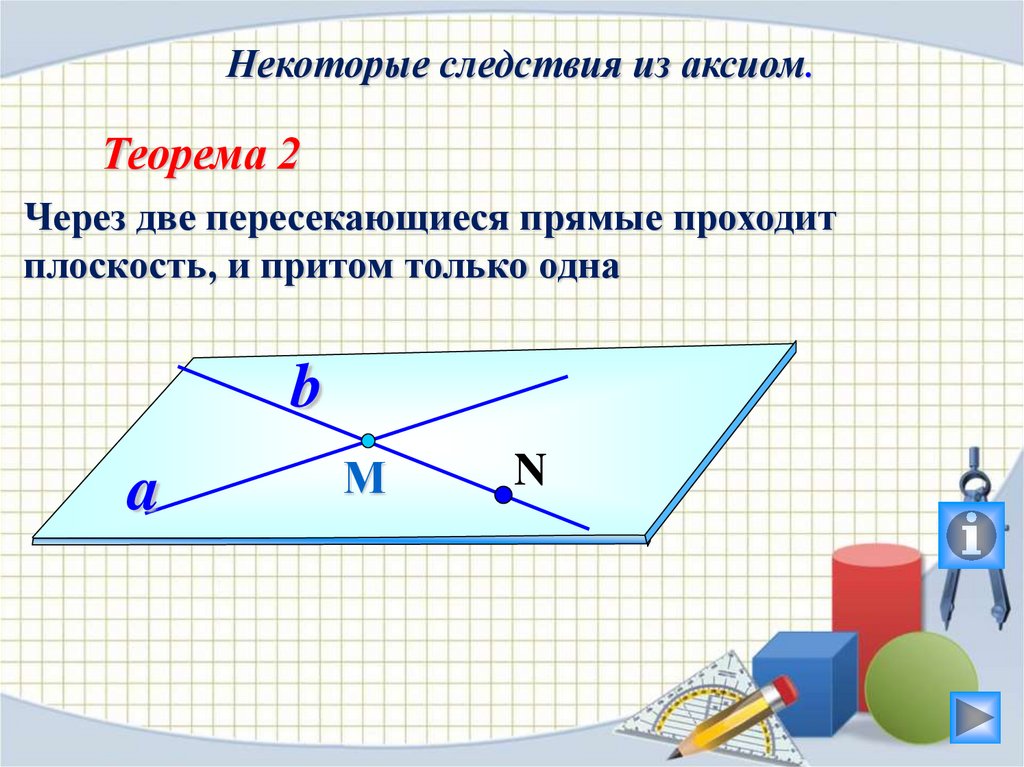
Некоторые следствия из аксиом.
Теорема 2
Через две пересекающиеся прямые проходит
плоскость, и притом только одна
b
a
М
N

17.

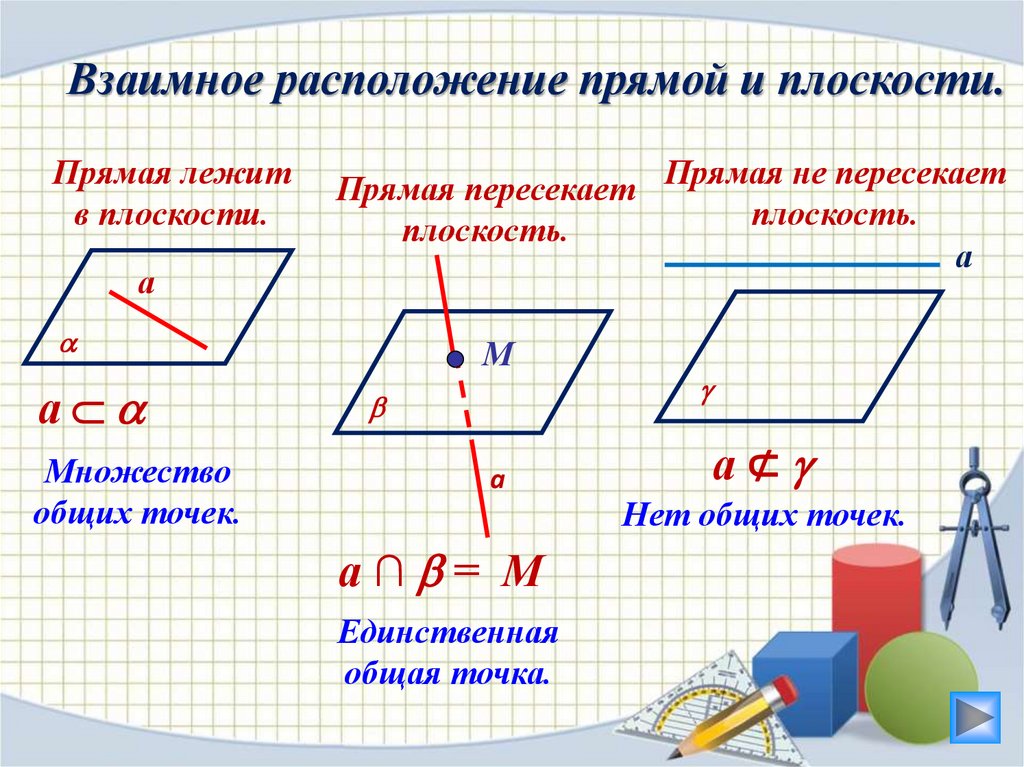
Взаимное расположение прямой и плоскости.
Прямая лежит
в плоскости.
а
Прямая пересекает Прямая не пересекает
плоскость.
плоскость.
а
а
Множество
общих точек.
М
а
а∩ = М
Единственная
общая точка.
а⊄
Нет общих точек.

18.

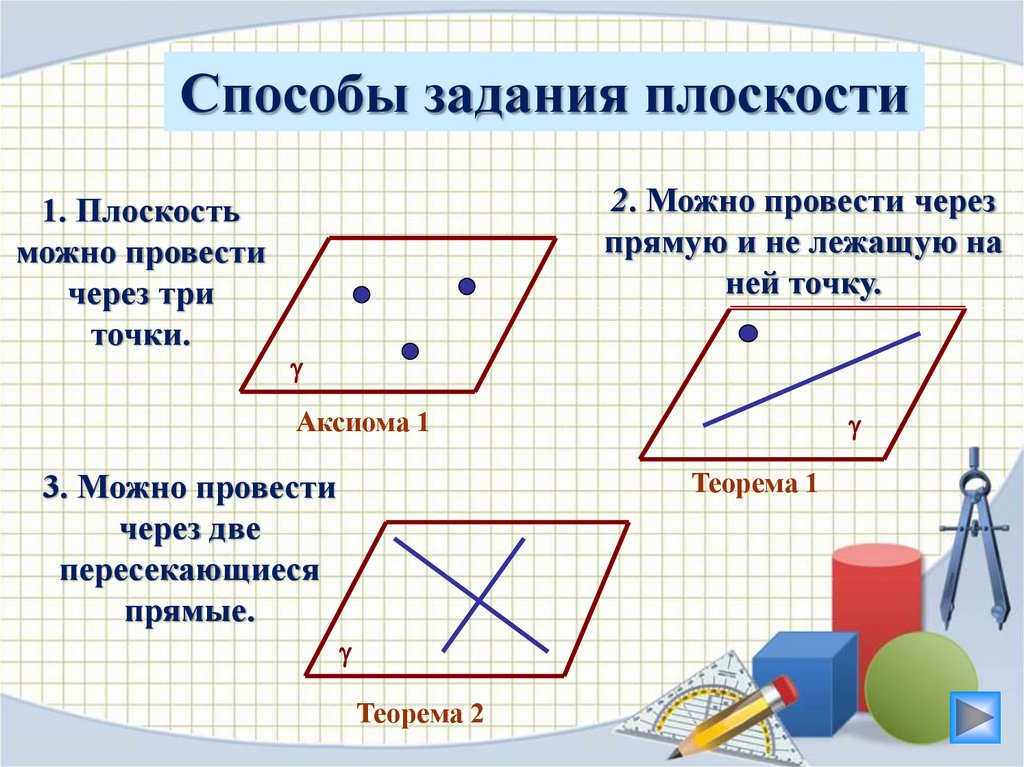
Способы задания плоскости
1. Плоскость
можно провести
через три
точки.
2. Можно провести через
прямую и не лежащую на
ней точку.
Аксиома 1
Теорема 1
3. Можно провести
через две
пересекающиеся
прямые.
Теорема 2

19.

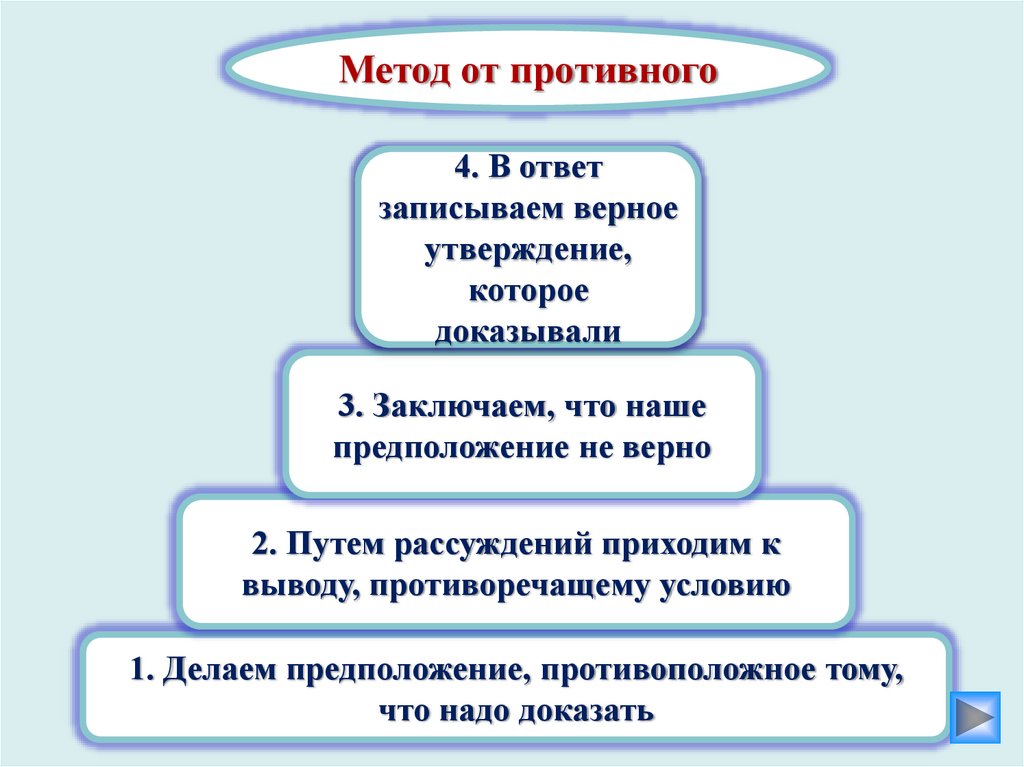
Метод от противного
4. В ответ
записываем верное
утверждение,
которое
доказывали
3. Заключаем, что наше
предположение не верно
2. Путем рассуждений приходим к
выводу, противоречащему условию
1. Делаем предположение, противоположное тому,
что надо доказать

20.

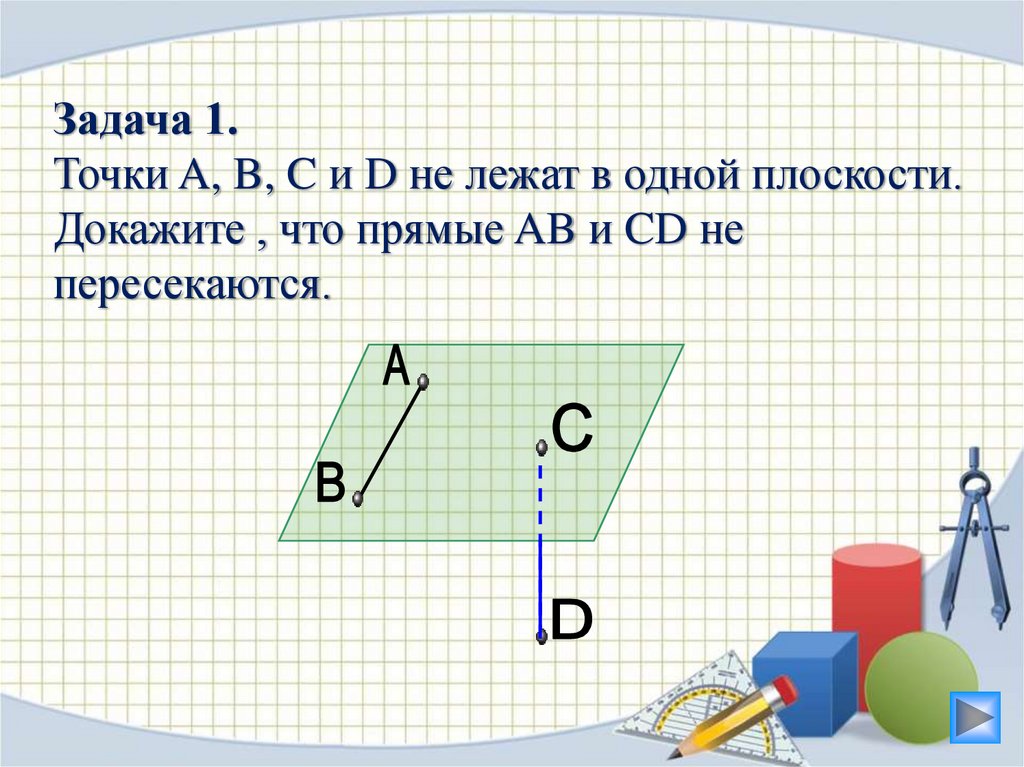
Задача 1.
Точки A, B, C и D не лежат в одной плоскости.
Докажите , что прямые AB и CD не
пересекаются.

21. Математический диктант

1). Сформулируйте аксиомы стереометрии.
• Аксиома 1. Через любые три точки, не
лежащие на одной прямой, проходит
плоскость и притом только одна.
• Аксиома 2. Если две точки прямой лежат в
плоскости, то и все точки этой прямой лежат
в этой плоскости.
• Аксиома 3. Если две плоскости имеют общую
точку, то они имеют общую прямую, на
которой лежат все общие точки этих
плоскостей.

22. Математический диктант

2). Заполните пропуски.
а). Для любой прямой существуют точки,
принадлежащие ей, и _______.
б). Через прямую и не лежащую на ней точку
проходит плоскость, и притом _______.
в). Через две пересекающиеся прямые проходит
плоскость, и притом _______.
г). Если А а, а , то А … .
д). Если А , В , С АВ, то С … .

23.

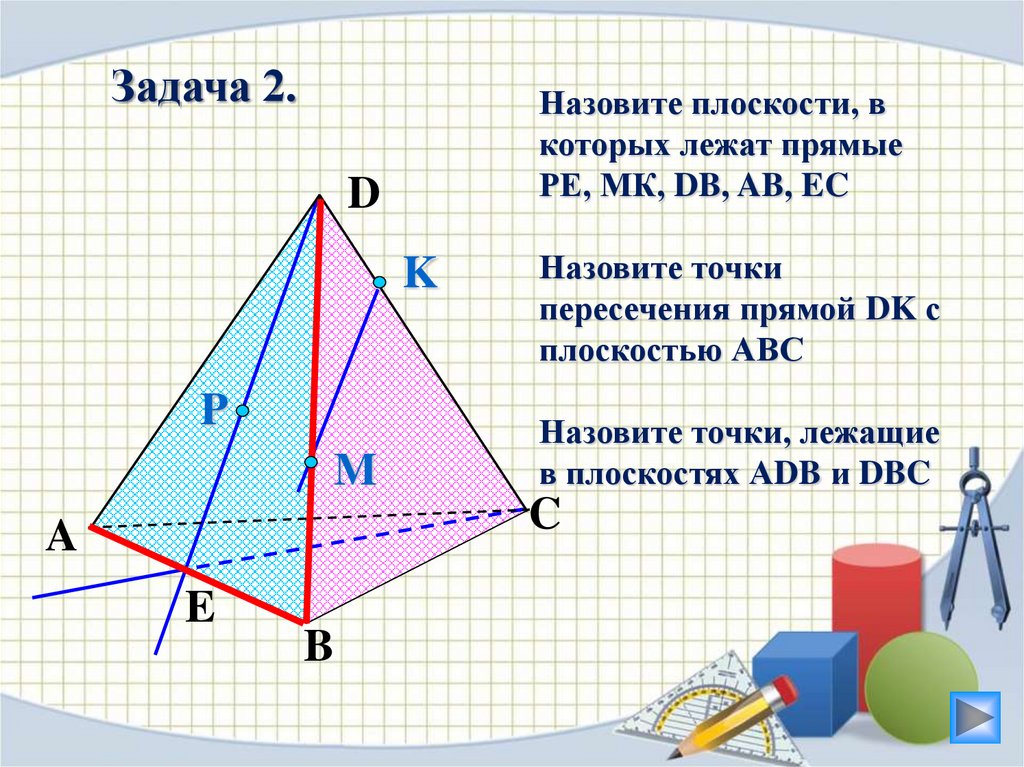
Задача 2.
Назовите плоскости, в
которых лежат прямые
РЕ, МК, DB, AB, EC
D
K
P
M
Назовите точки
пересечения прямой DK с
плоскостью АВС
Назовите точки, лежащие
в плоскостях АDB и DBC
C
A
E
B

24.

Задача 3.
B1
Q
P
A1
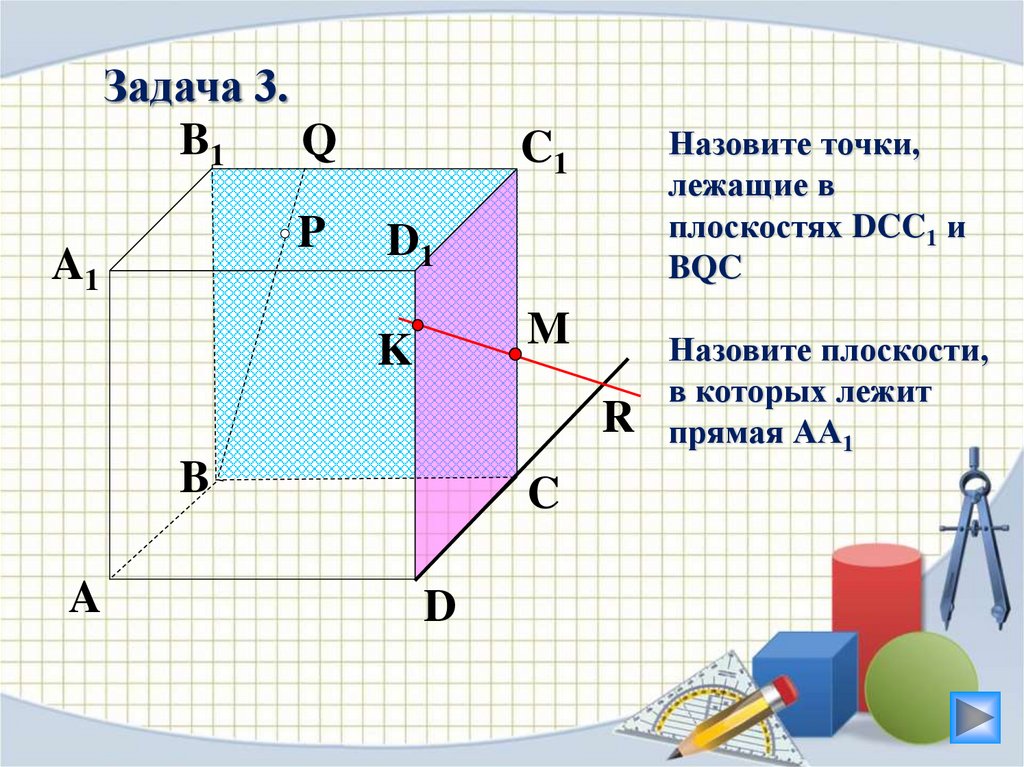
Назовите точки,
лежащие в
плоскостях DCC1 и
BQC
C1
D1
M
K
R
B
A
C
D
Назовите плоскости,
в которых лежит
прямая АА1

25. Самостоятельная работа.

II Уровень
• Прямые а, b и с имеют общую точку. Верно ли, что
данные прямые лежат в одной плоскости? Ответ
объясните.
III Уровень
• Четыре прямые попарно пересекаются. Верно
ли, что если любые три из них лежат в одной
плоскости, то все четыре прямые лежат в
одной плоскости? Ответ объясните.

26. Ответы.

II Уровень
• По Теореме 2 через две пересекающиеся
прямые проходит единственная плоскость.
Рассмотрим эту плоскость и третью прямую:
у них есть одна точка пересечения по
условию. И тут возможно два варианта: либо
прямая пересекает плоскость в этой точке,
либо вся лежит в этой плоскости.

27. Ответы.

28. Подведение итогов.

1. Рассмотрели сходства и различия
планиметрии и стереометрии.
2. Изучили аксиомы стереометрии и
некоторые следствия из них.
3. Научились применять полученные
знания при решении задач.
4. Домашнее задание.