Similar presentations:
Стереометрия. Аксиомы стереометрии
1. «Стереометрия Аксиомы стереометрии»
ГОБПОУ(ЛМсК)Липецкий машиностроительный колледж
Презентация на тему:
«Стереометрия
Аксиомы стереометрии»
Выполнил:
Студент 1го. Курса
Гр.Э-19-2
Денисов Павел
Александрович
2.
Стереометрия - изучает свойства фигурв пространстве.
Слово «стереометрия» происходит от
греческих слов «стереос» объемный,
пространственный, «метрео» – мерить.
Основные фигуры: точка, прямая,
плоскость.
3.
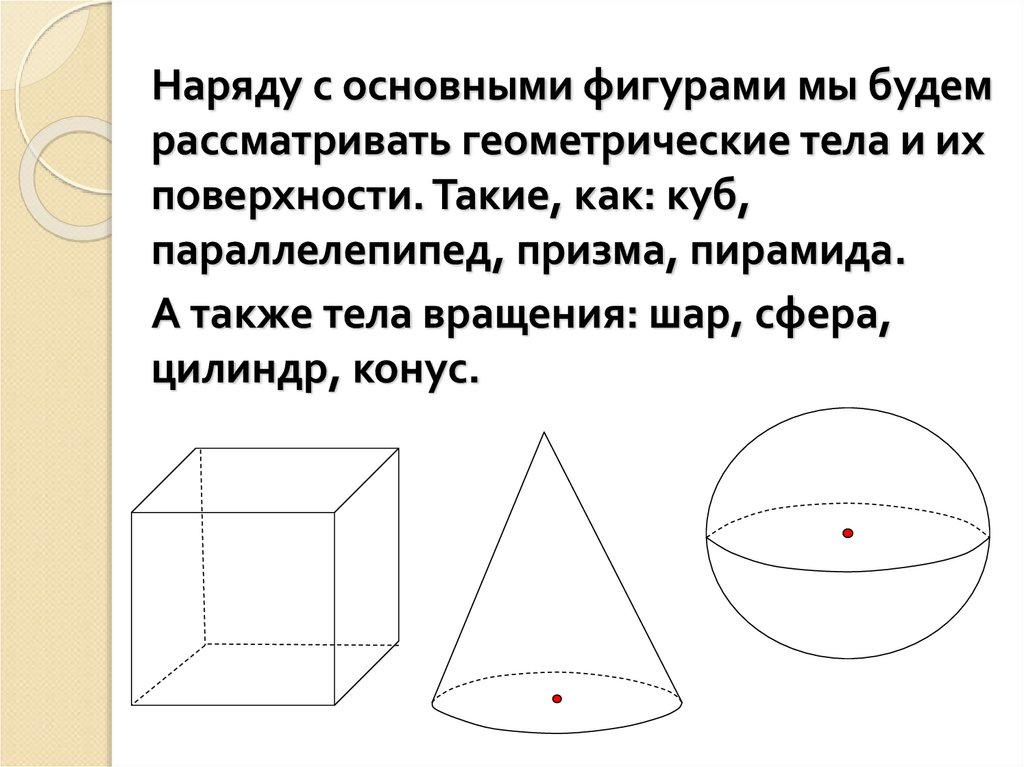
Наряду с основными фигурами мы будемрассматривать геометрические тела и их
поверхности. Такие, как: куб,
параллелепипед, призма, пирамида.
А также тела вращения: шар, сфера,
цилиндр, конус.
4.
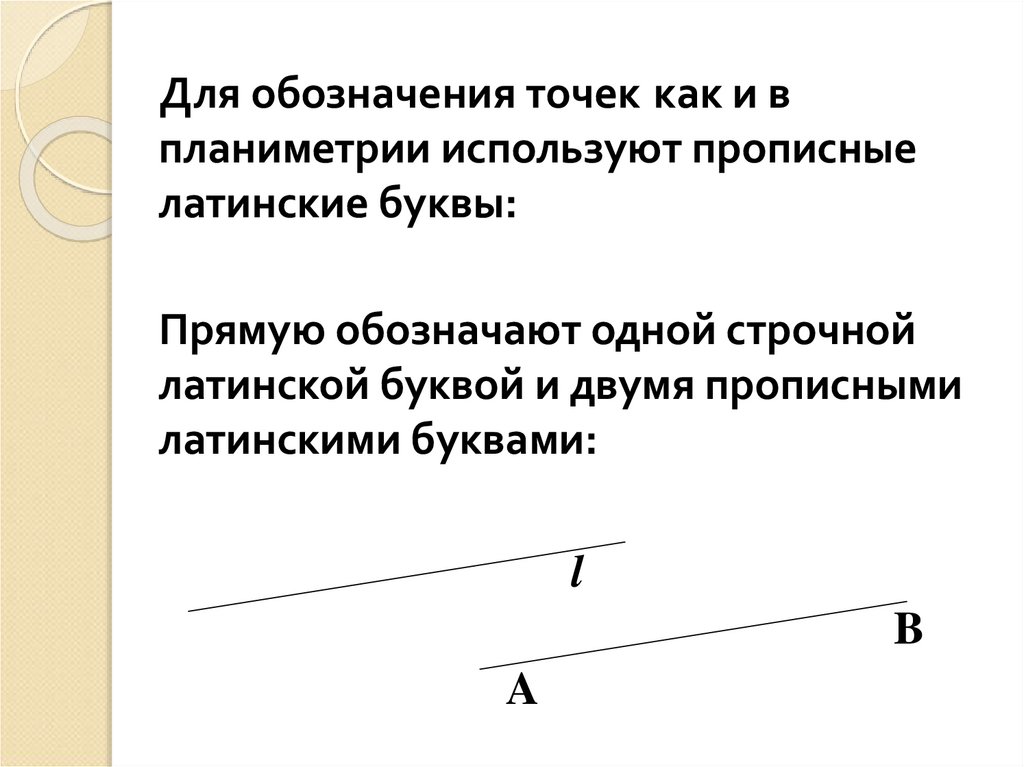
Для обозначения точек как и впланиметрии используют прописные
латинские буквы:
Прямую обозначают одной строчной
латинской буквой и двумя прописными
латинскими буквами:
l
B
A
5.
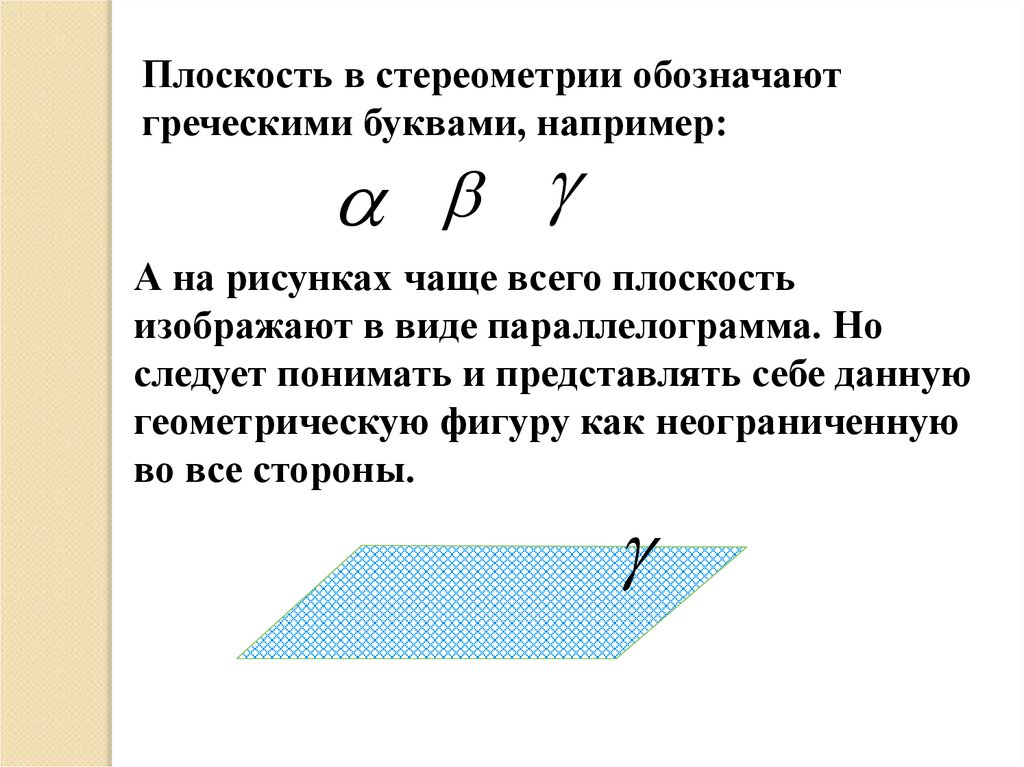
Плоскость в стереометрии обозначаютгреческими буквами, например:
А на рисунках чаще всего плоскость
изображают в виде параллелограмма. Но
следует понимать и представлять себе данную
геометрическую фигуру как неограниченную
во все стороны.
6.
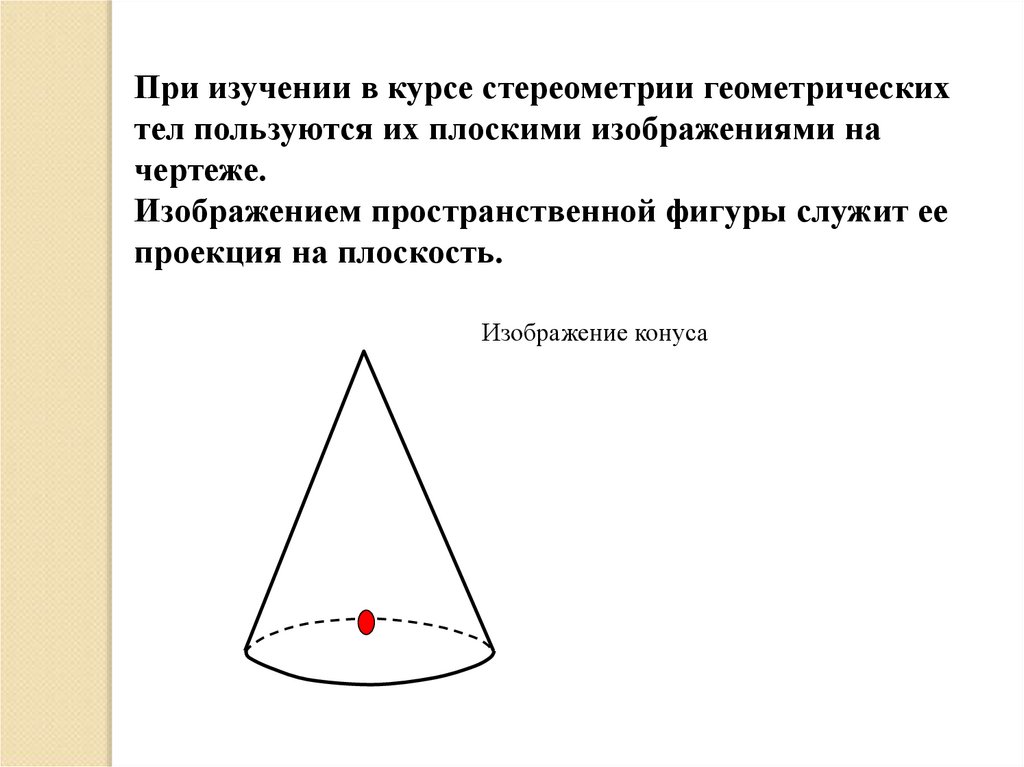
При изучении в курсе стереометрии геометрическихтел пользуются их плоскими изображениями на
чертеже.
Изображением пространственной фигуры служит ее
проекция на плоскость.
Изображение конуса
7.
Изучая свойства геометрических фигур –воображаемых объектов, мы получаем представление
о геометрических свойствах реальных предметов (их
форме, взаимном расположении и т. д.) и можем
использовать эти свойства в практической
деятельности. В этом состоит прикладное значение
геометрии.
Геометрия, в частности стереометрия, широко
используется в строительном деле, архитектуре,
машиностроении, геодезии, во многих
других областях науки и техники.
8.
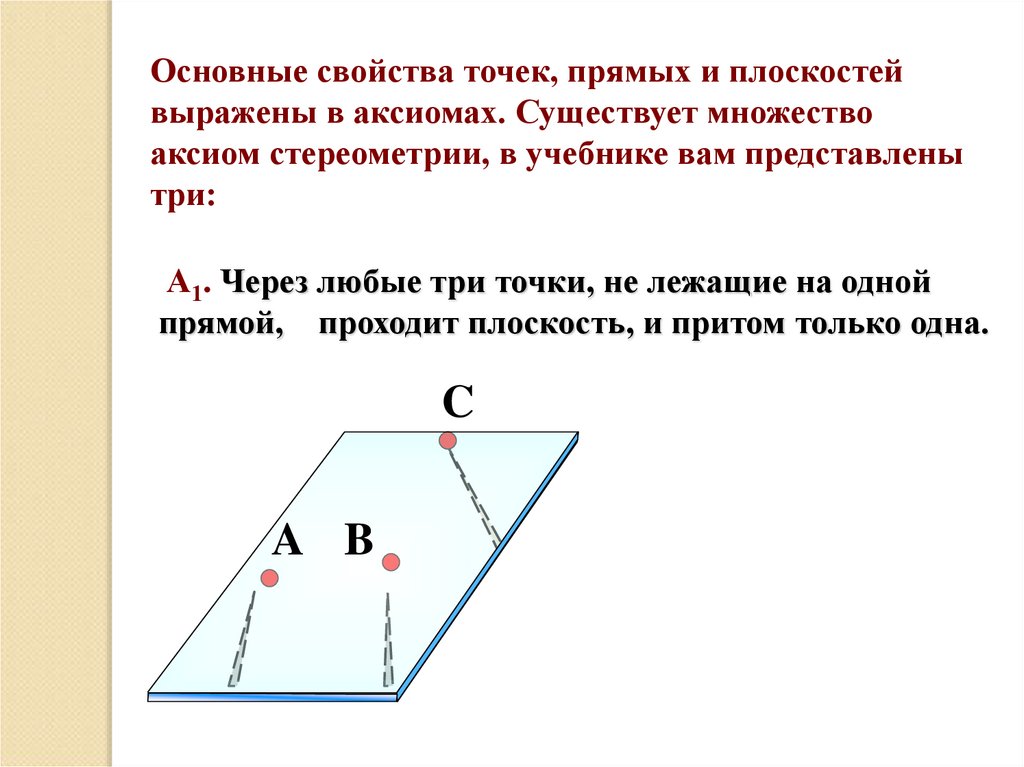
Основные свойства точек, прямых и плоскостейвыражены в аксиомах. Существует множество
аксиом стереометрии, в учебнике вам представлены
три:
А1. Через любые три точки, не лежащие на одной
прямой, проходит плоскость, и притом только одна.
C
A B
9.
Самый простой пример к аксиоме А1 изповседневной жизни:
Табурет с тремя ножками всегда
идеально встанет на пол и не будет
качаться. У табурета с четырьмя
ножками бывают проблемы с
устойчивостью, если ножки стула не
одинаковые по длине.
Табурет качается, т. е. опирается на три
ножки, а четвертая ножка (четвертая
«точка») не лежит в плоскости
пола, а висит в воздухе.
10.
А2. Если две точки прямой лежат в плоскости, то всеточки прямой лежат в этой плоскости.
B
A
a
А
В
а
11.
Свойство, выраженное в аксиоме А2, используется дляпроверки «ровности» чертежной линейки.
Линейку прикладывают краем к плоской поверхности
стола. Если край линейки ровный, то он всеми своими
точками прилегает к поверхности стола.
Если край неровный, то в каких-то местах между ним
и поверхностью стола образуется просвет.
12.
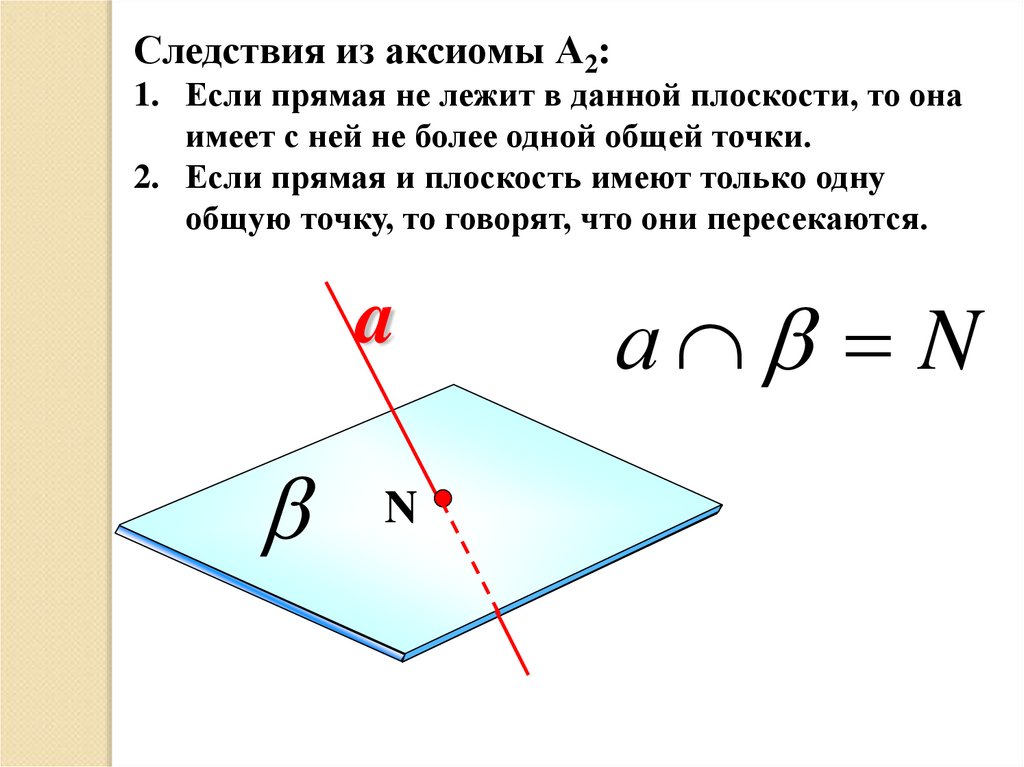
Следствия из аксиомы А2:1. Если прямая не лежит в данной плоскости, то она
имеет с ней не более одной общей точки.
2. Если прямая и плоскость имеют только одну
общую точку, то говорят, что они пересекаются.
a
N
а N
13.
А3. Если две плоскости имеют общую точку, то ониимеют общую прямую, на которой лежат все общие
точки этих плоскостей.
Самый простой
пример к аксиоме
А3 из повседневной
жизни
является
пересечение двух
смежных стен
комнаты.
a
a
14.
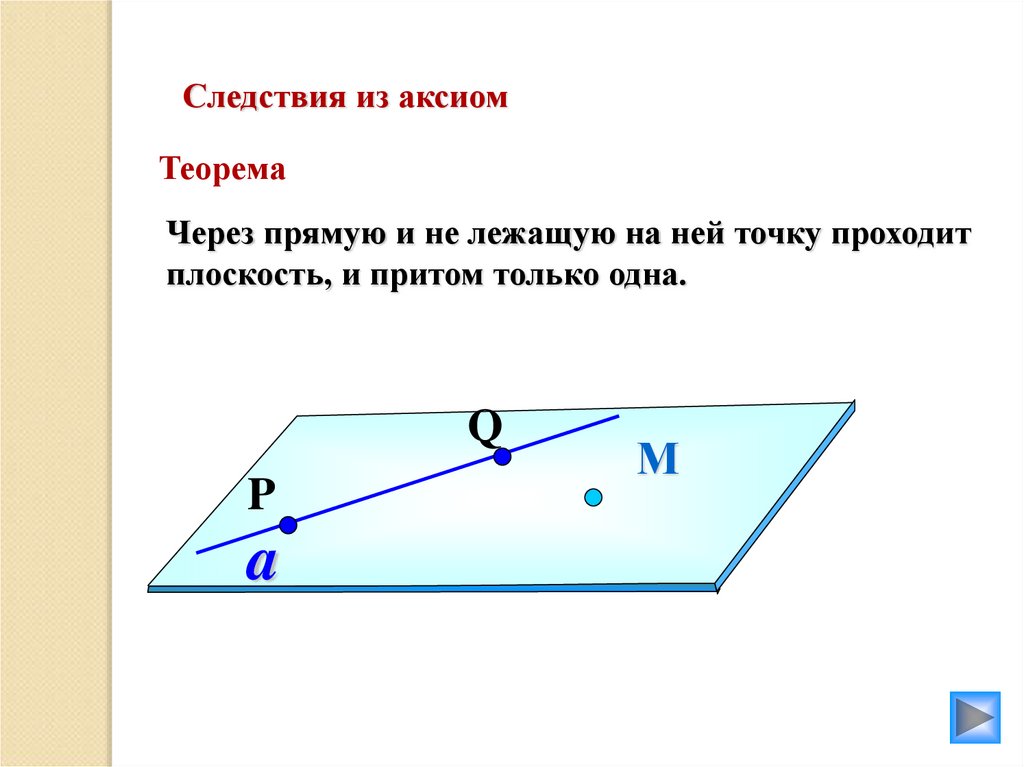
Следствия из аксиомТеорема
Через прямую и не лежащую на ней точку проходит
плоскость, и притом только одна.
Q
P
a
М
15.
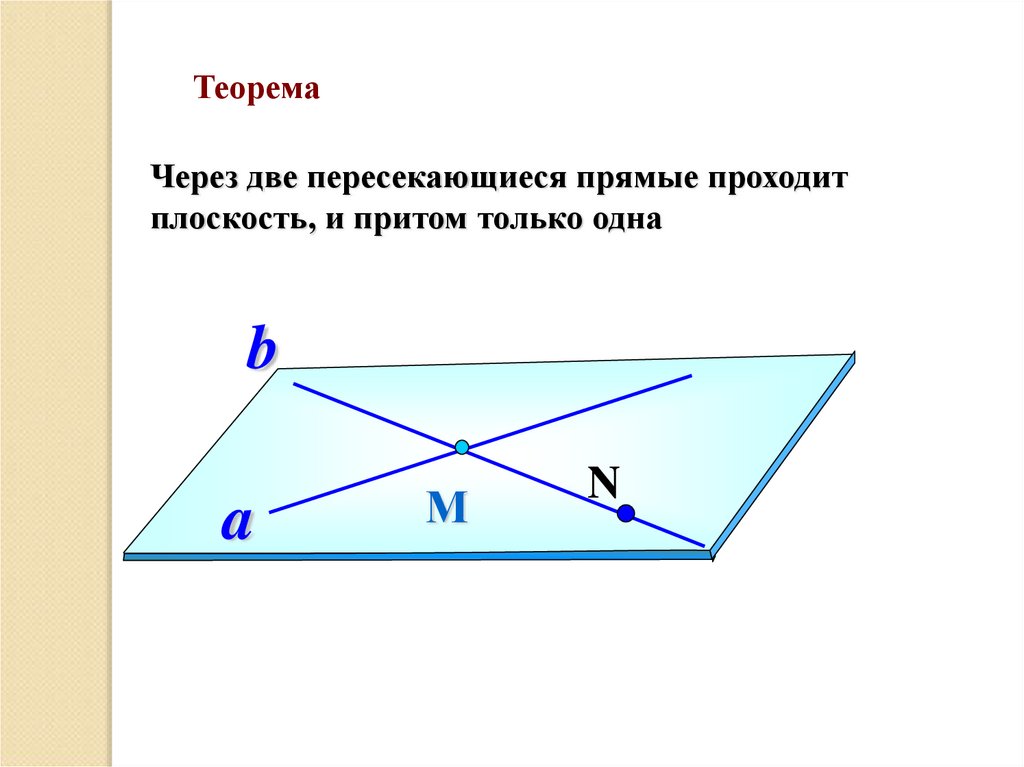
ТеоремаЧерез две пересекающиеся прямые проходит
плоскость, и притом только одна
b
a
М
N
16.
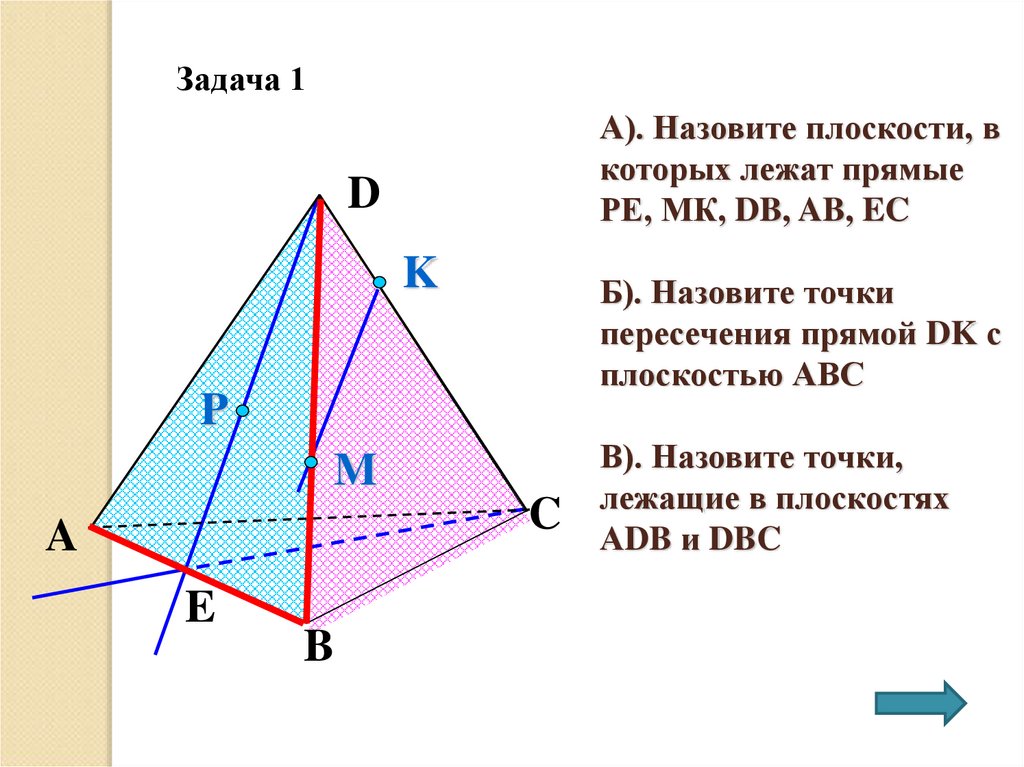
Задача 1А). Назовите плоскости, в
которых лежат прямые
РЕ, МК, DB, AB, EC
D
K
Б). Назовите точки
пересечения прямой DK с
плоскостью АВС
P
M
C
A
E
B
В). Назовите точки,
лежащие в плоскостях
АDB и DBC
17.
а) Прямая РЕ лежит в плоскости ADB, таккак точки Р и Е принадлежат плоскости
ADB, а через две точки можно провести
единственную прямую.Прямая МК лежит в
плоскости DBС, так как точки М и К
принадлежат плоскости DBС.Прямая DB
лежит в плоскостях ADB и DBС и является
линией пересечения этих
плоскостей.Прямая АB лежит в плоскостях
ADB и АBС и является линией
пересечения этих плоскостей. Прямая ЕС
лежит в плоскости ABС.
в) В плоскости ADB лежат точки A, D, B, P и
Е.В плоскости DBС лежат точки D, B, С, К и
М.г) Плоскости АВС и DBC пересекаются
по прямой ВС,плоскости АВD и СDА
пересекаются по прямой АD,плоскости РDС
и АВС пересекаются по прямой
б) Прямая DK пересекает
плоскость АВС в точке С,
так как точка С
принадлежит прямой DK и
плоскости АВС.Прямая СЕ
пересекает плоскость АDВ
в точке Е, так как точка Е
принадлежит прямой СЕ и
плоскости









 mathematics
mathematics








