Similar presentations:
Аксиомы стереометрии
1.
Аксиомыстереометрии
2. Геометрия (греч.)
наука о свойствах геометрических фигургео –земля
метрео - измерять
3. Геометрия
Планиметрияот лат. planum —
плоскость и... метрия
Стереометрия
от др.-греч. στερεός, «стереос» —
«пространственный,объемный»
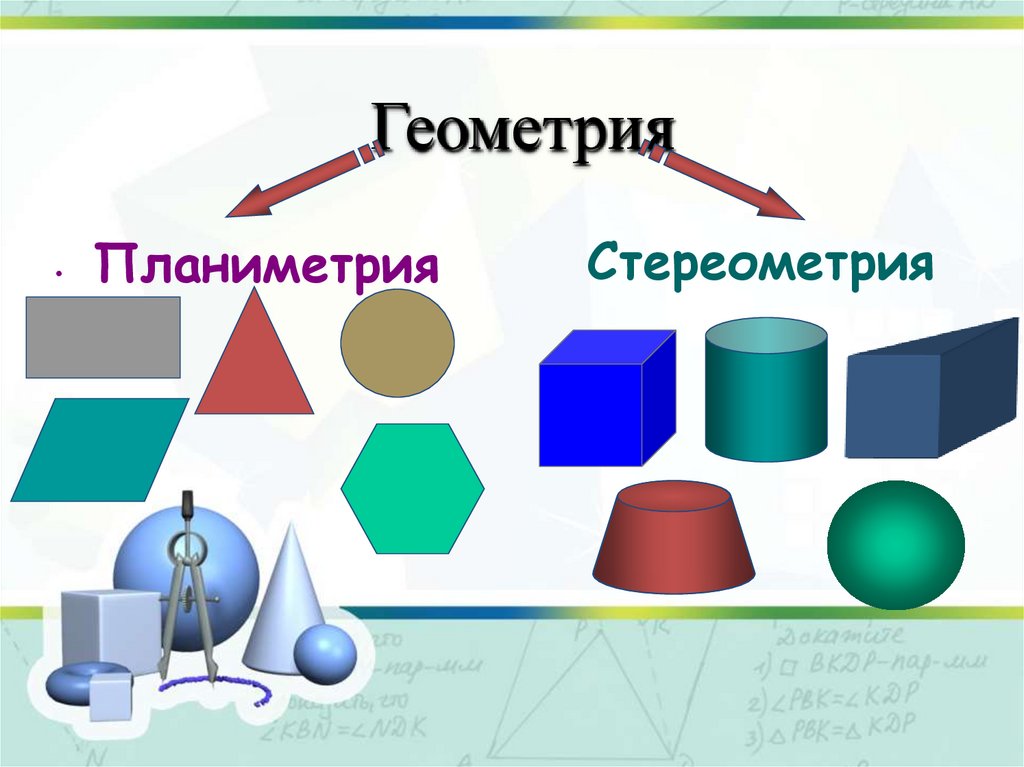
4. Геометрия
Планиметрия
Стереометрия
5.
раздел геометрии, в котором изучаютсясвойства тел в пространстве
6.
Евклид — жил около 300 г. до н. э,первый математик Александрийской школы.
Его
главная
работа
«Начала»
содержит
изложение планиметрии, стереометрии.
Его называют «отцом геометрии».
Дави́д Ги́льберт
(1862-1943)
—
немецкий математик-универсал,
внёс значительный вклад в развитие многих
областей математики.
Разработал аксиоматику евклидовой геометрии.
7.
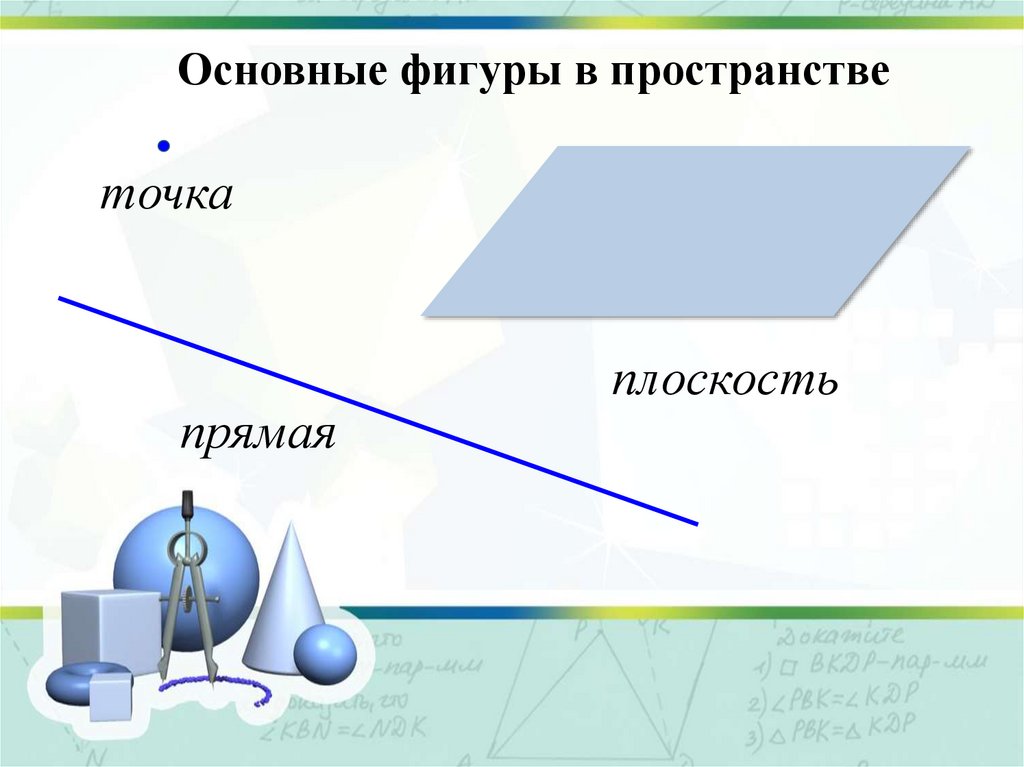
Основные фигуры в пространстветочка
прямая
плоскость
8.
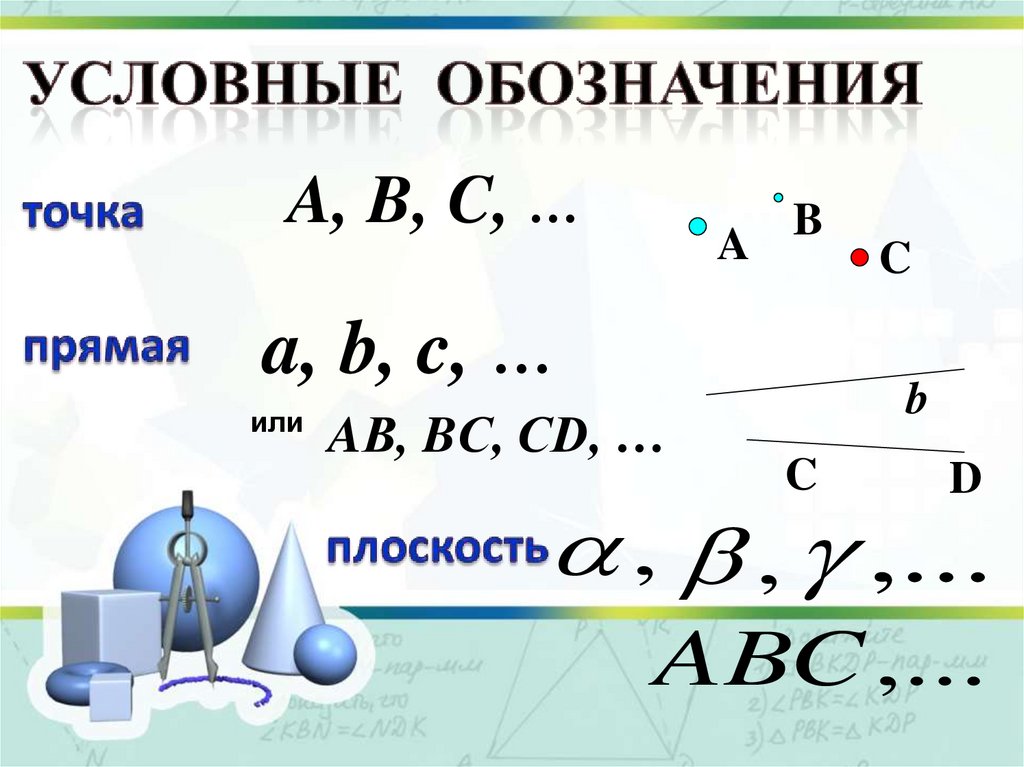
A, B, C, …A
B
a, b, c, …
или
AВ, BС, CD, …
C
b
C
D
, , ,...
ABC ,...
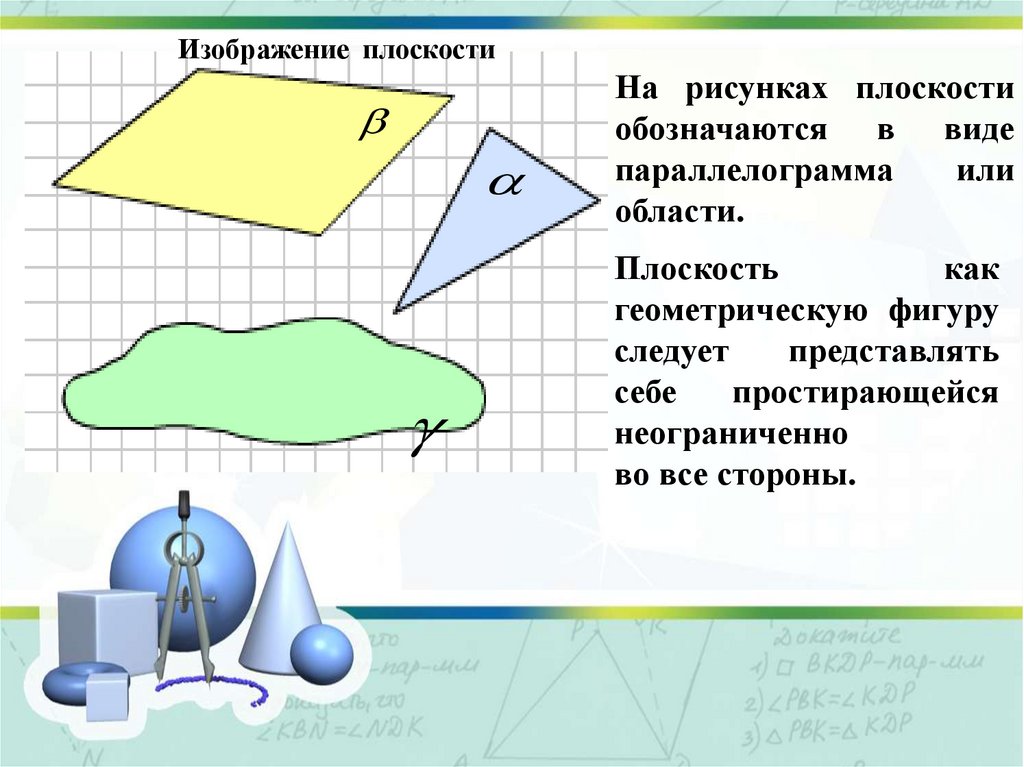
9. Изображение плоскости
На рисунках плоскостиобозначаются в виде
параллелограмма
или
области.
Плоскость
как
геометрическую фигуру
следует
представлять
себе
простирающейся
неограниченно
во все стороны.
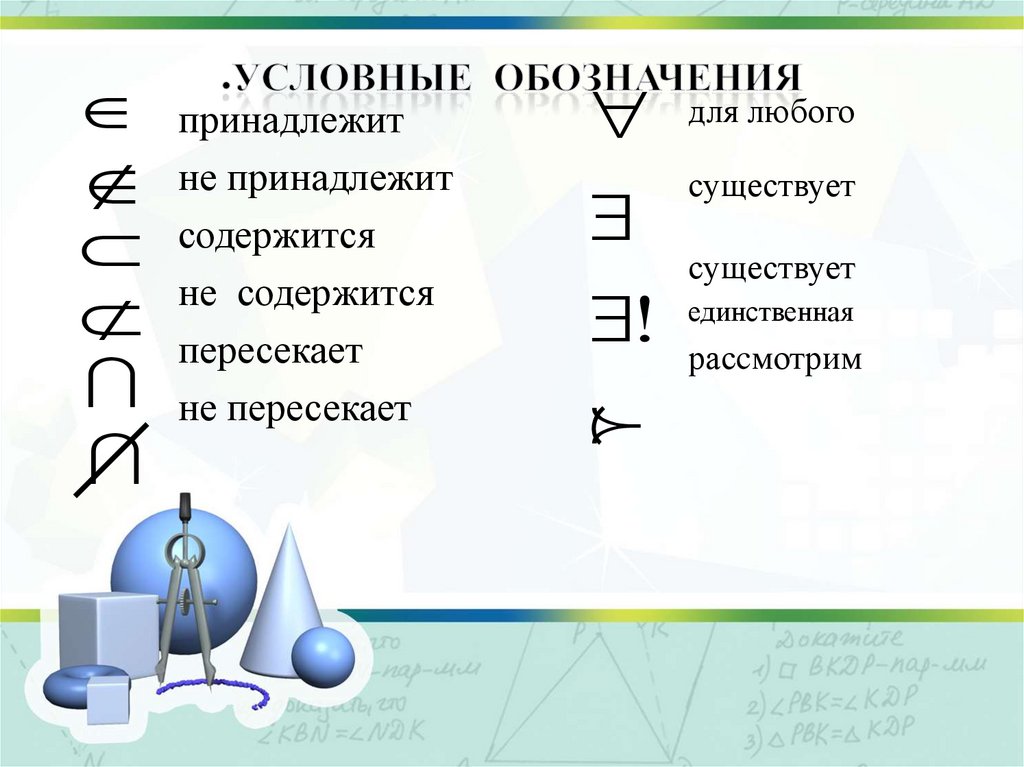
10. Условные обозначения
принадлежитне принадлежит
содержится
не содержится
пересекает
не пересекает
для любого
существует
существует
единственная
! расcмотрим
11. Что такое аксиома?
АКСИОМА (axíõma - греческое слово, означающее «бесспорноеположение») – это высказывание,
принимается без доказательства.
истинность
которого
Аксиомы были сформулированы Евклидом ( III в. до н. э.) в его знаменитом
сочинении «Начала».
На основе аксиом доказываются теоремы и строится вся геометрия
12.
Аксиомы стереометрииВ
А
С
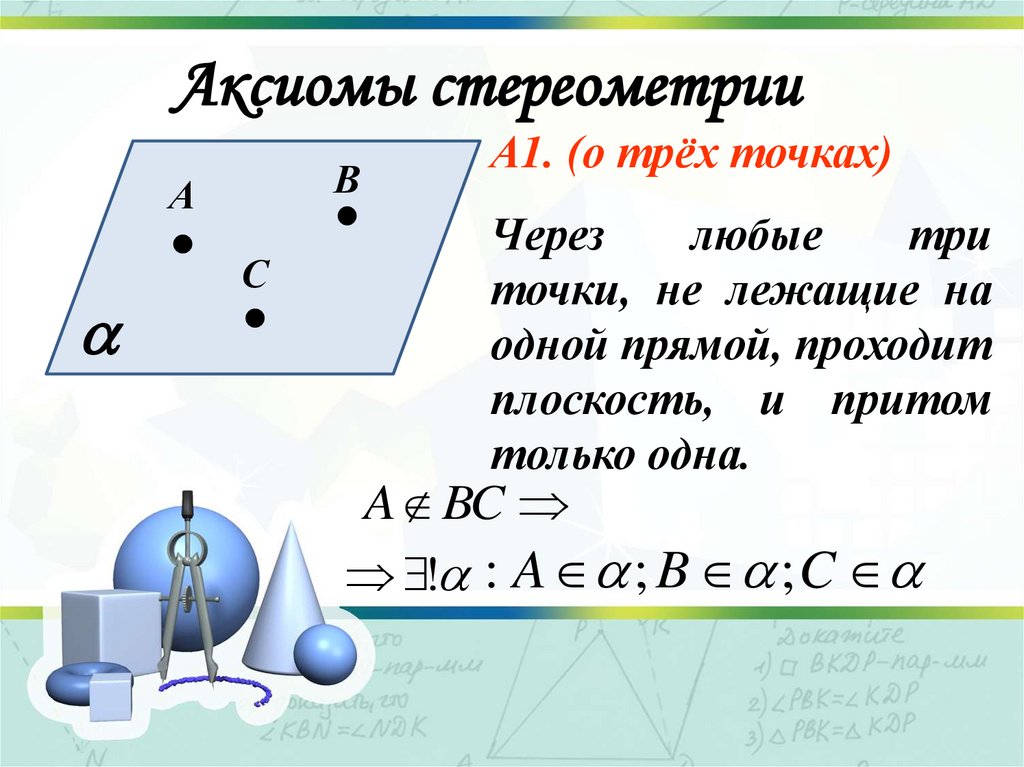
А1. (о трёх точках)
Через
любые
три
точки, не лежащие на
одной прямой, проходит
плоскость, и притом
только одна.
A BC
! : A ; B ; C
13.
Иллюстрации к аксиоме А1:Табурет с тремя ножками всегда
идеально встанет на пол и не будет
качаться.
14.
Для видеокамеры, фотосъемки и для других приборов частоиспользуют штатив – треногу. Три ножки штатива устойчиво
расположатся на любом полу в помещениях, на асфальте или
прямо на газоне на улице, на песке на пляже или в траве в
лесу. Три ножки штатива всегда найдут плоскость.
15.
Аксиомы стереометрииB
a
A
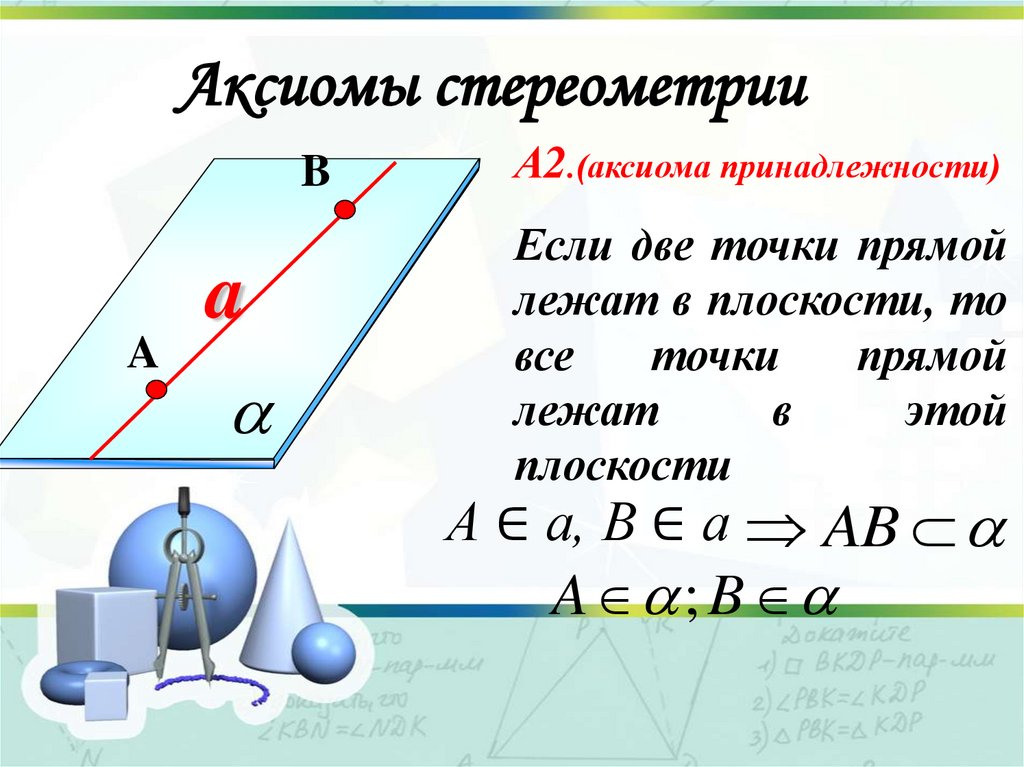
А2.(аксиома принадлежности)
Если две точки прямой
лежат в плоскости, то
все
точки
прямой
лежат
в
этой
плоскости
А ∈ а, В ∈ а AB
A ; B
16.
Свойство, выраженное в аксиоме А2, используется для проверки «ровности» чертежнойлинейки. Линейку прикладывают краем к плоской поверхности стола. Если край линейки
ровный, то он всеми своими точками прилегает к поверхности стола. Если край неровный
то в каких-то местах между ним и поверхностью стола образуется просвет.
17.
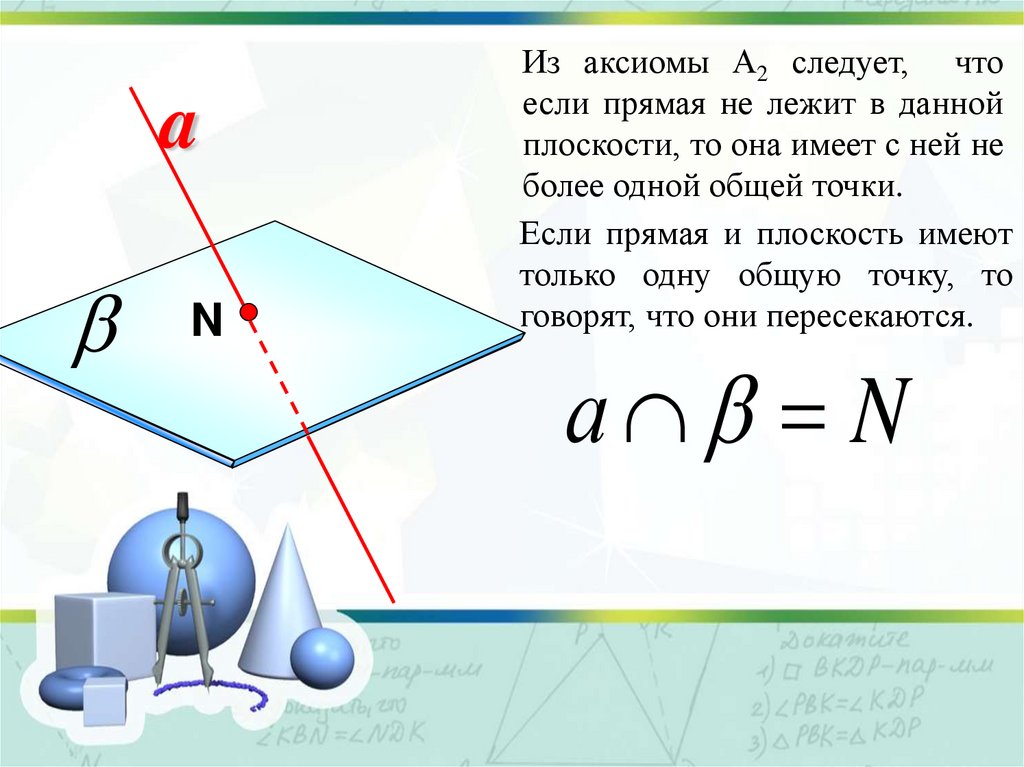
aN
Из аксиомы А2 следует, что
если прямая не лежит в данной
плоскости, то она имеет с ней не
более одной общей точки.
Если прямая и плоскость имеют
только одну общую точку, то
говорят, что они пересекаются.
а N
18.
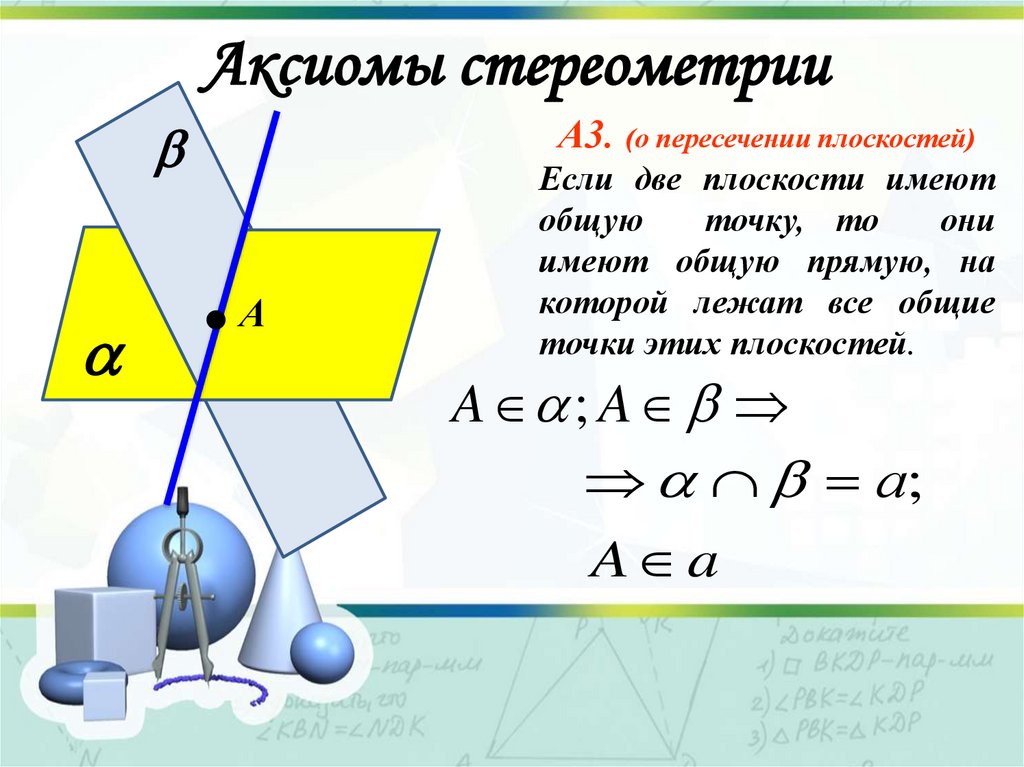
Аксиомы стереометрииА3. (о пересечении плоскостей)
А
Если две плоскости имеют
общую
точку, то
они
имеют общую прямую, на
которой лежат все общие
точки этих плоскостей.
A ; A
а;
A a
19.
Наглядной иллюстрацией аксиомы А3является пересечение двух смежных стен,
стены и потолка классной комнаты.
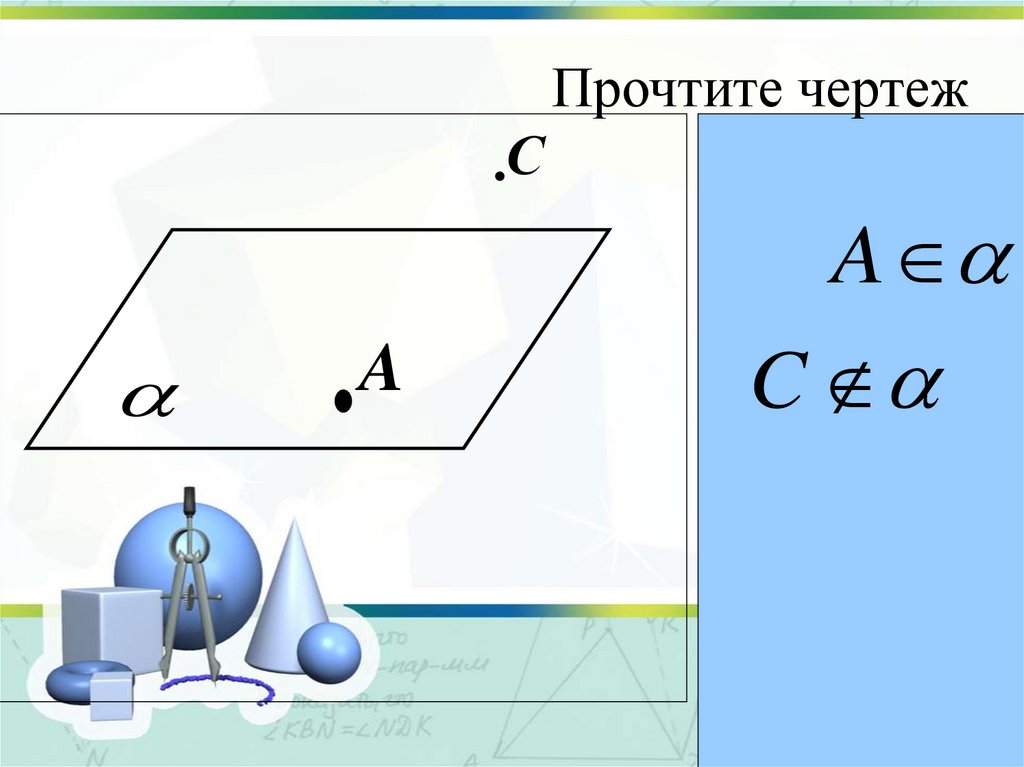
20. Прочтите чертеж
СA
A
C
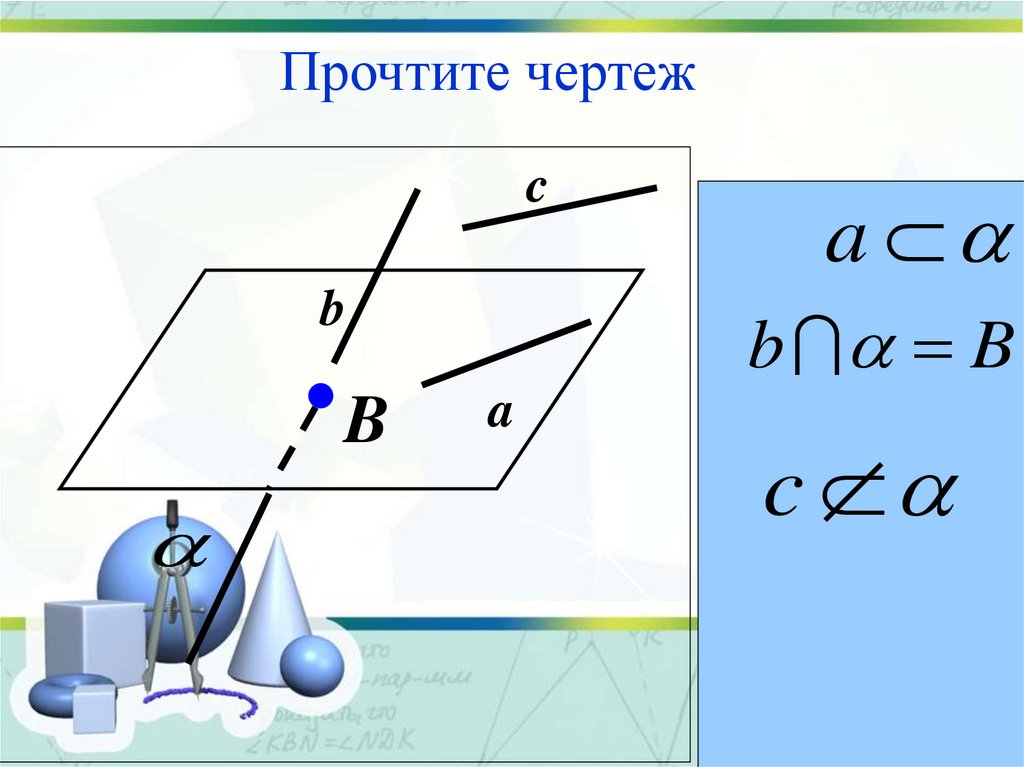
21.
Прочтите чертежc
b
B
a
b B
a
c
22.
23.
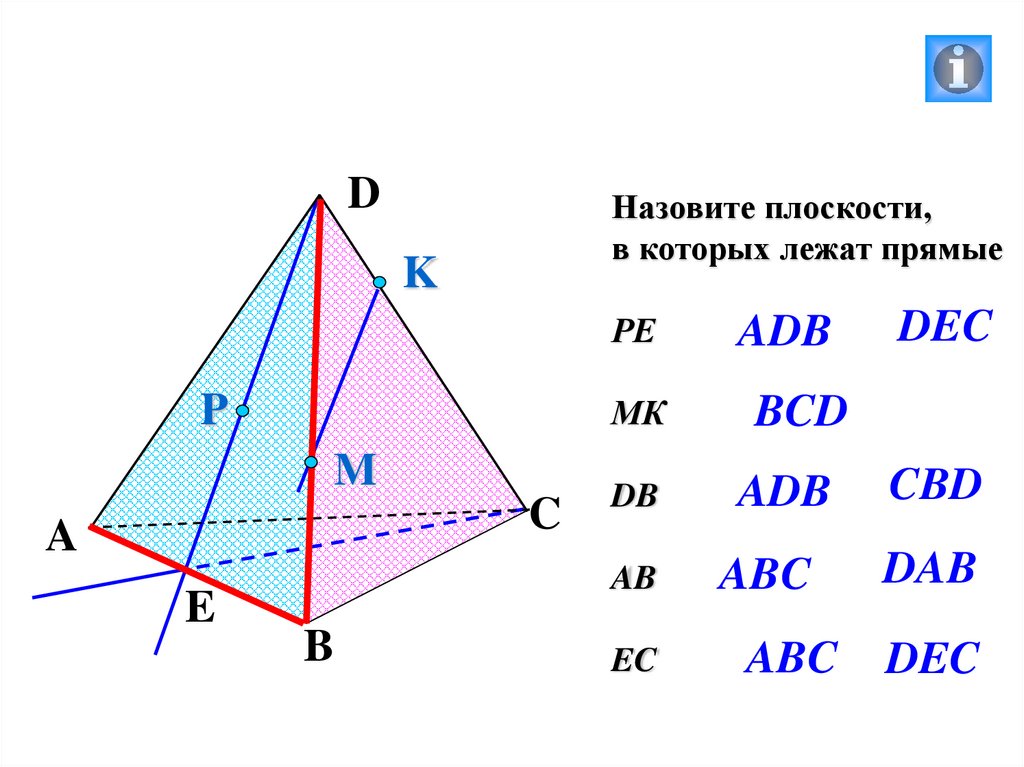
DНазовите плоскости,
в которых лежат прямые
K
P
M
C
A
E
B
DEC
РЕ
ADB
МК
BCD
DB
ADB
CBD
AB
ABC
DAB
ABC
DEC
EC
24.
НазовитеD
K
точки пересечения
прямой DK с плоскостью
АВС,
DK ∩ ABC = C
P
M
A
E
B
прямой СЕ с плоскостью
АDB.
C
СЕ ∩ ADB = E
25.
DK
P
M
A
E
B
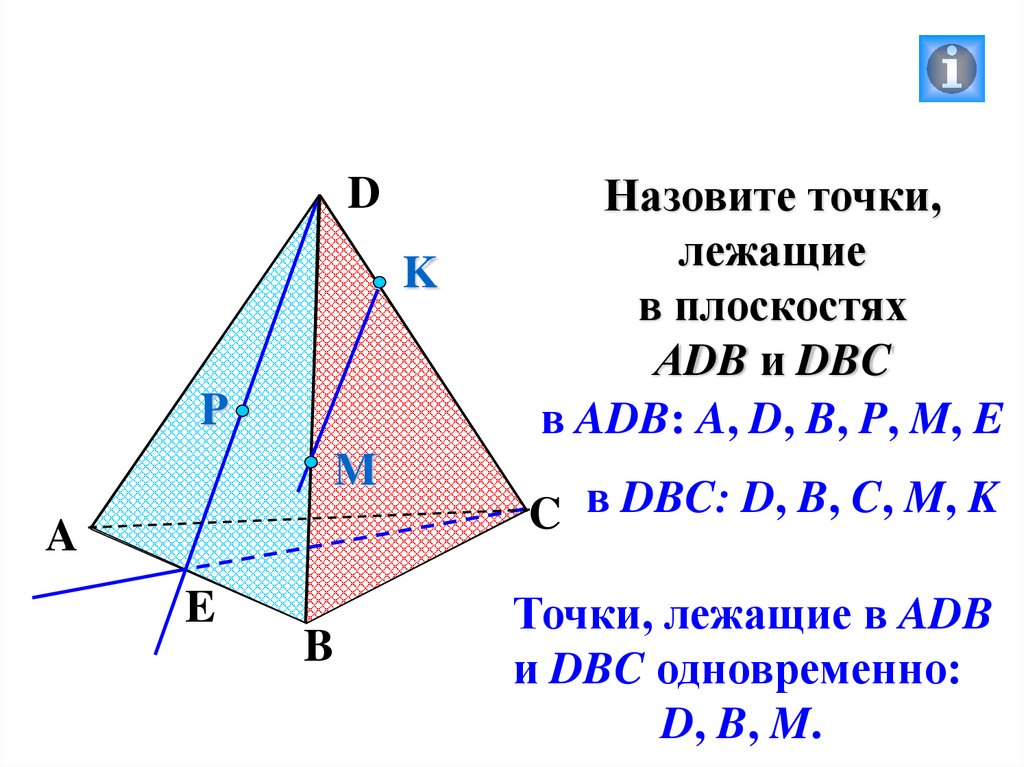
Назовите точки,
лежащие
в плоскостях
АDB и DBC
в ADB: A, D, B, P, M, E
C в DBC: D, B, C, M, K
Точки, лежащие в ADB
и DBC одновременно:
D, B, M.
26.
№2B1
Q
P
A1
C1
D1
K
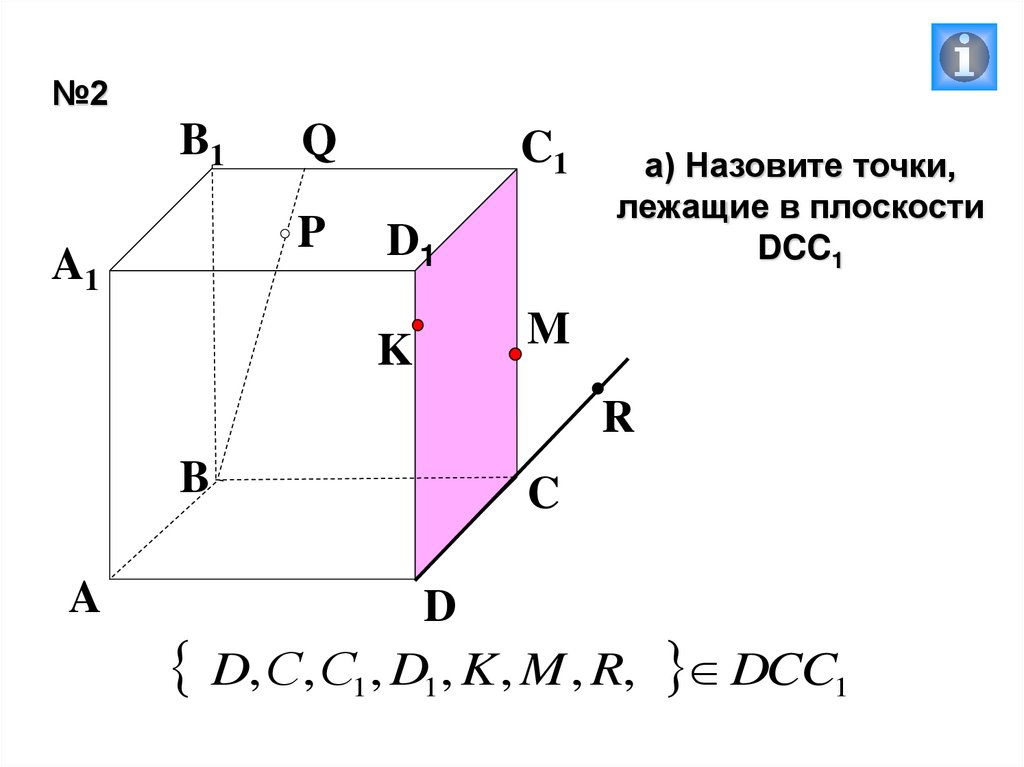
а) Назовите точки,
лежащие в плоскости
DCC1
M
R
B
A
C
D
D, С, С1, D1, K , M , R, DCC1
27.
B1Q
P
A1
C1
D1
K
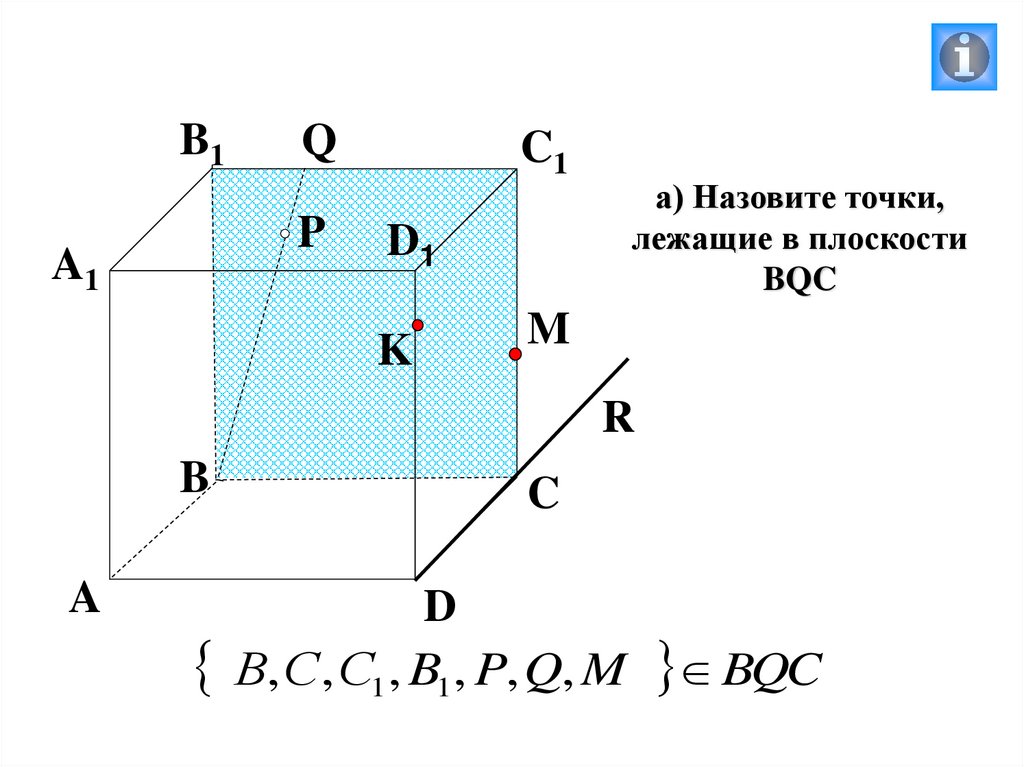
а) Назовите точки,
лежащие в плоскости
BQC
M
R
B
A
C
D
В, С, С1, B1, P, Q, M BQC
28.
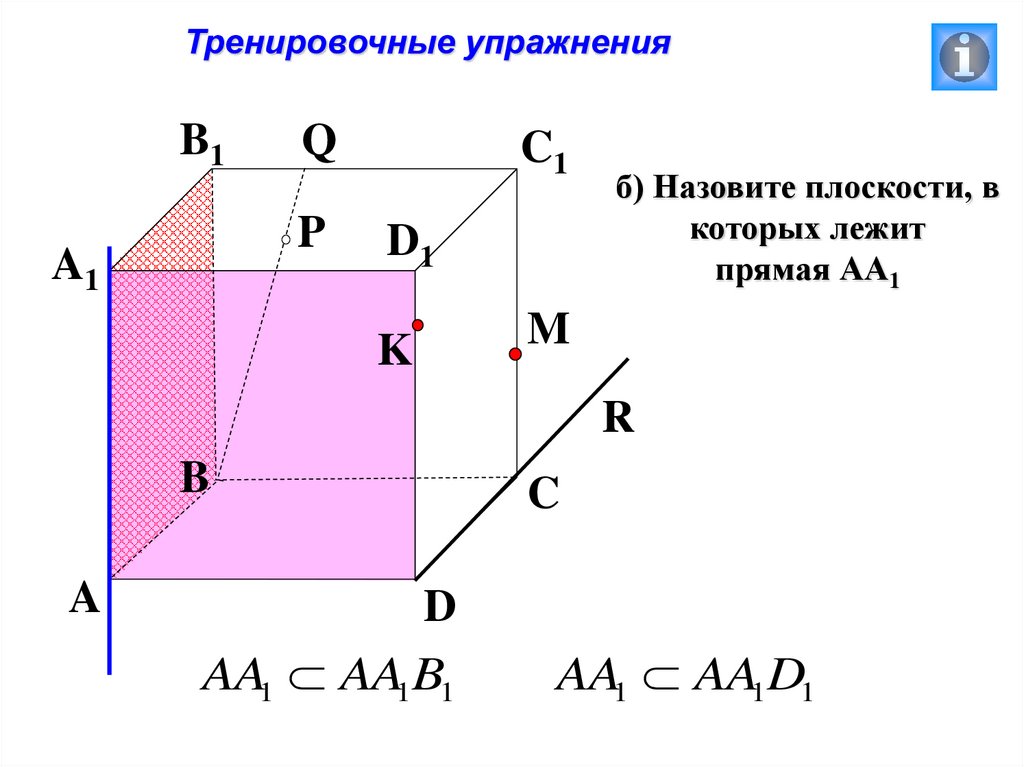
Тренировочные упражненияB1
Q
P
A1
C1
D1
K
б) Назовите плоскости, в
которых лежит
прямая АА1
M
R
A
B
C
D
AA1 AA1B1
AA1 AA1D1
29.
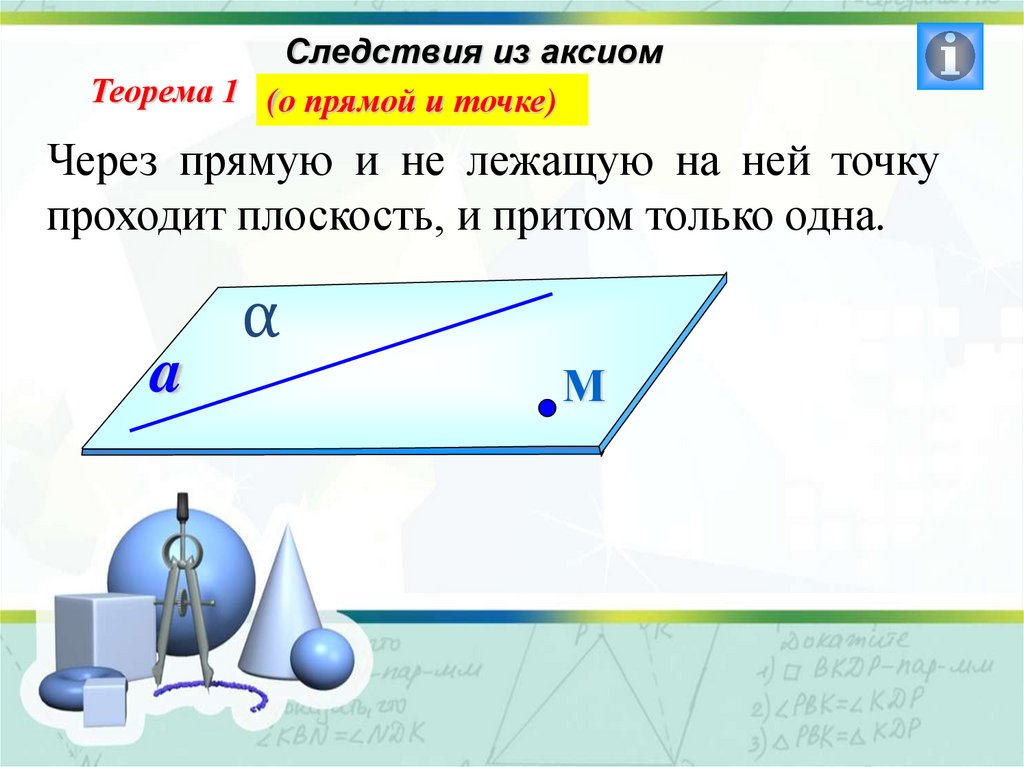
Следствия из аксиомТеорема 1 (о прямой и точке)
Через прямую и не лежащую на ней точку
проходит плоскость, и притом только одна.
a
⍺
М
30.
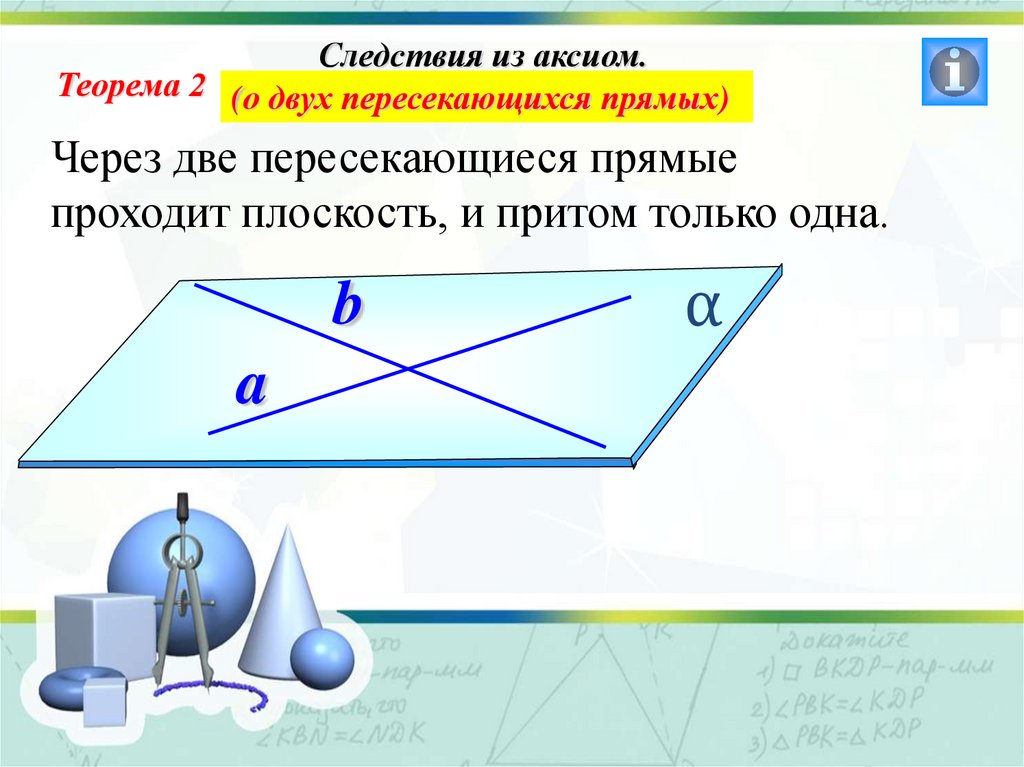
Следствия из аксиом.Теорема 2 (о двух пересекающихся прямых)
Через две пересекающиеся прямые
проходит плоскость, и притом только одна.
b
a
⍺
31.
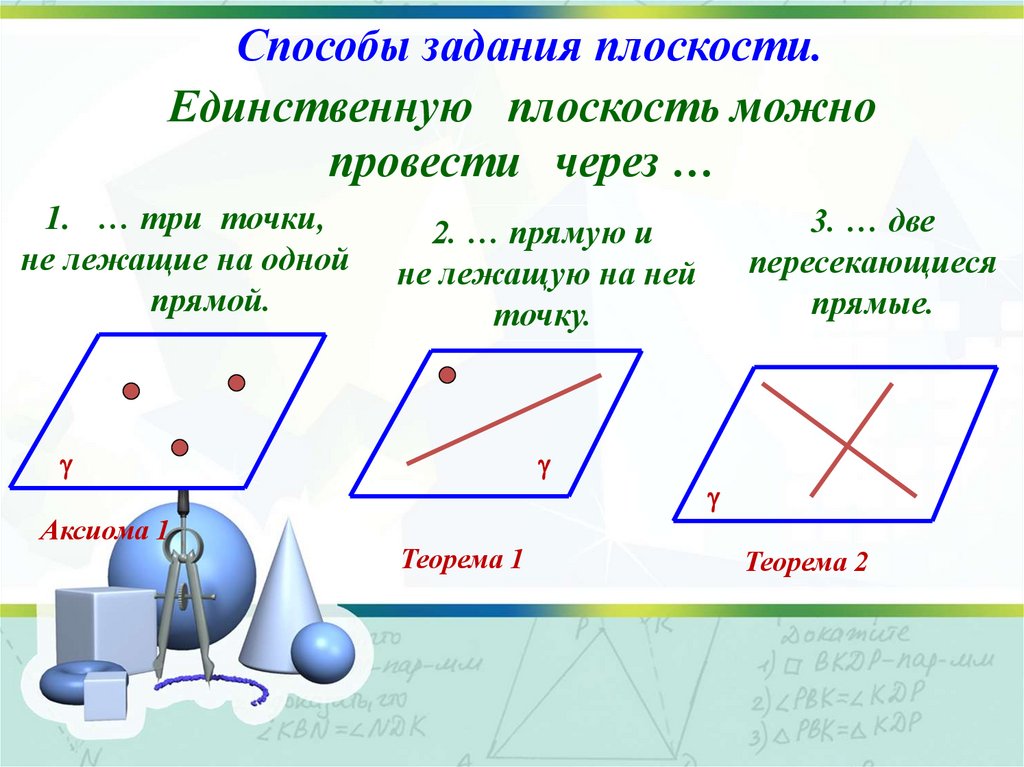
Способы задания плоскости.Единственную плоскость можно
провести через …
1. … три точки,
не лежащие на одной
прямой.
Аксиома 1
3. … две
пересекающиеся
прямые.
2. … прямую и
не лежащую на ней
точку.
Теорема 1
Теорема 2











 mathematics
mathematics








