Функция y=sinx

1.

2.

y
y = sin x
2
2
т
3
2
1
-1
2
x
3
2
2

3.

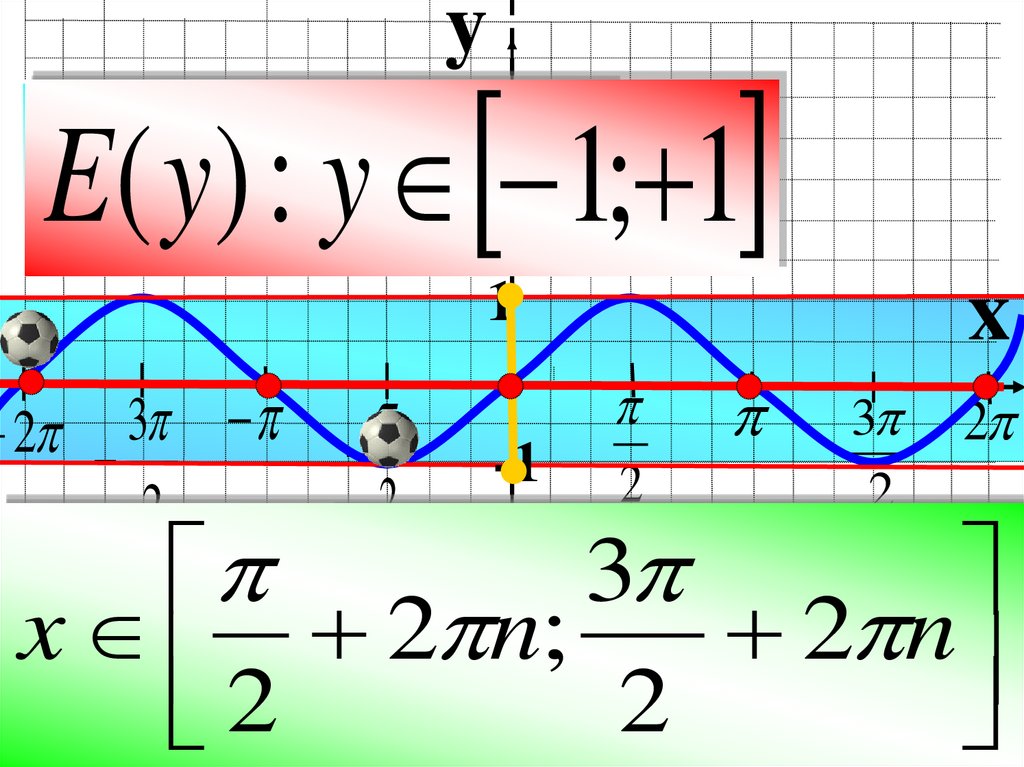
y
ED((yy))::yx R1; 1
x
1
2 3
2
2
-1
2
3
2
2
3
=2n ;n;n, n
xy = 0 x 2
2 nZ
22
22

4.

yy 00
x 0;
y
x
1
2 3
2
2
-1
2
3
2
2
x
2 nx;2 n ;2 ;n0
x

5.

Преобразование
графиков

6.

y
y = sin x 2
x
1
2 3
2
2
-1
2
E ( y ) : y [1; 3]
3
2
2

7.

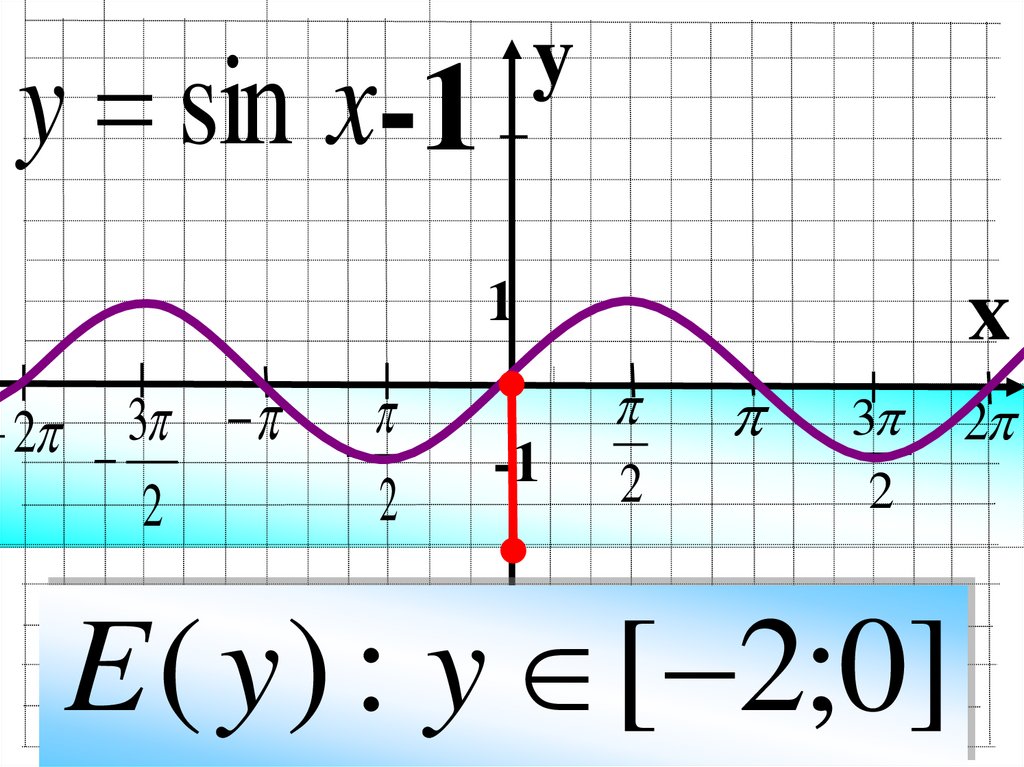
y = sin x-1
y
x
1
2 3
2
2
-1
2
3
2
E ( y ) : y [ 2;0]
2

8.

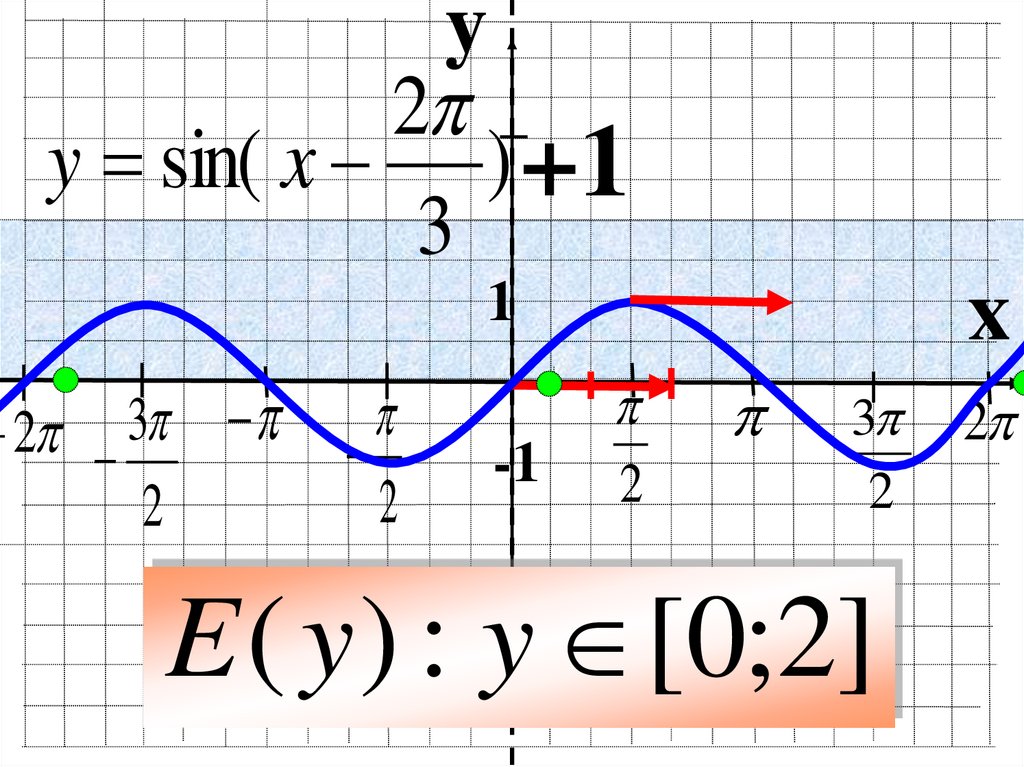
y
2
y = sin( x ) +1
3
x
1
2 3
2
2
-1
2
3
2
E ( y ) : y [0;2]
2

9.

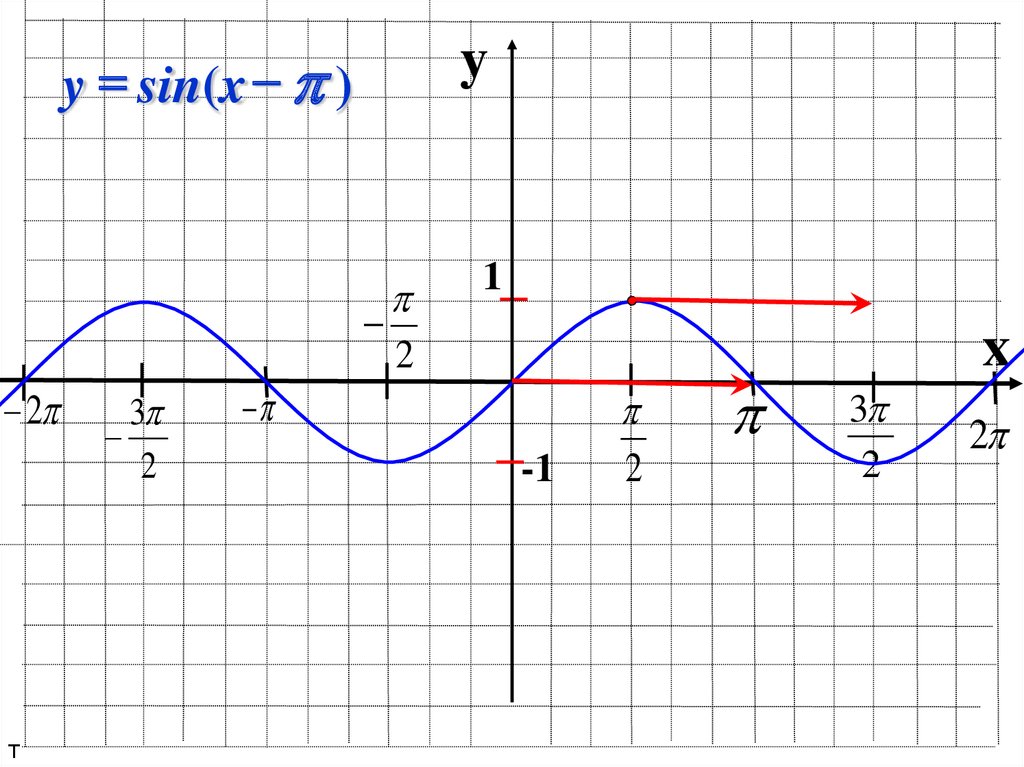
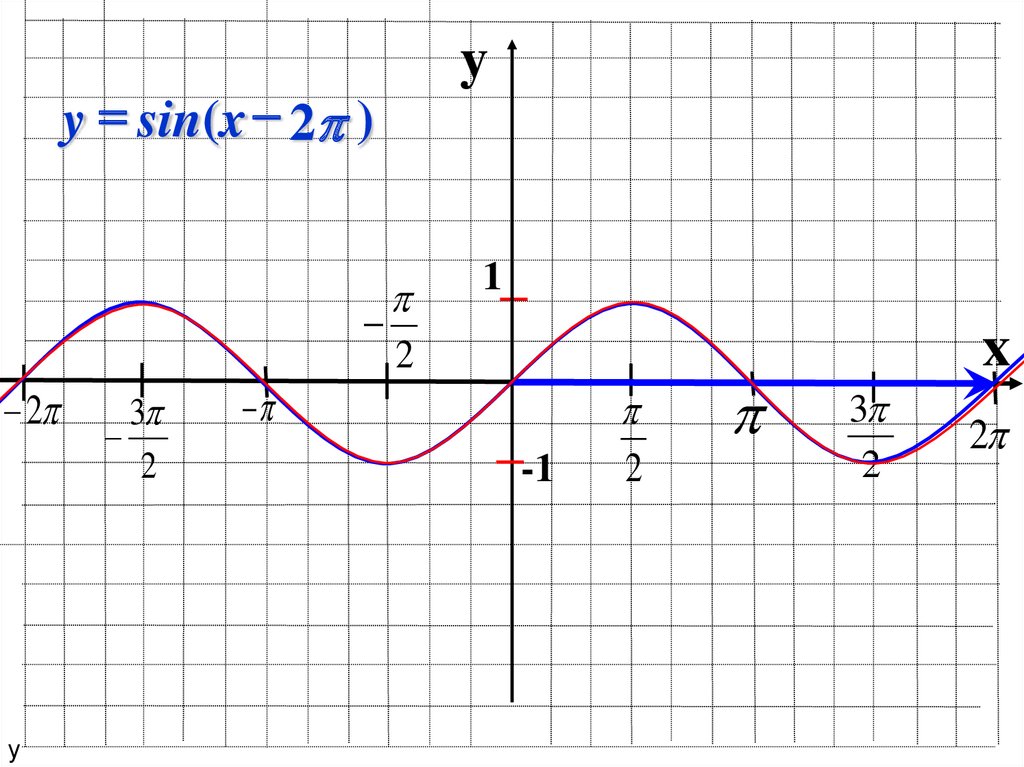
y = sin(x )
y
2
2
т
3
2
1
-1
2
x
3
2
2

10.

y = sin(x 2 )
2
2
у
3
2
y
1
-1
2
x
3
2
2

11.

y
y = sin(x )
3
2
2
т
3
2
1
-1
2
x
3
2
2

12.

13.

2 3
2
y
x
1
2
-1
2
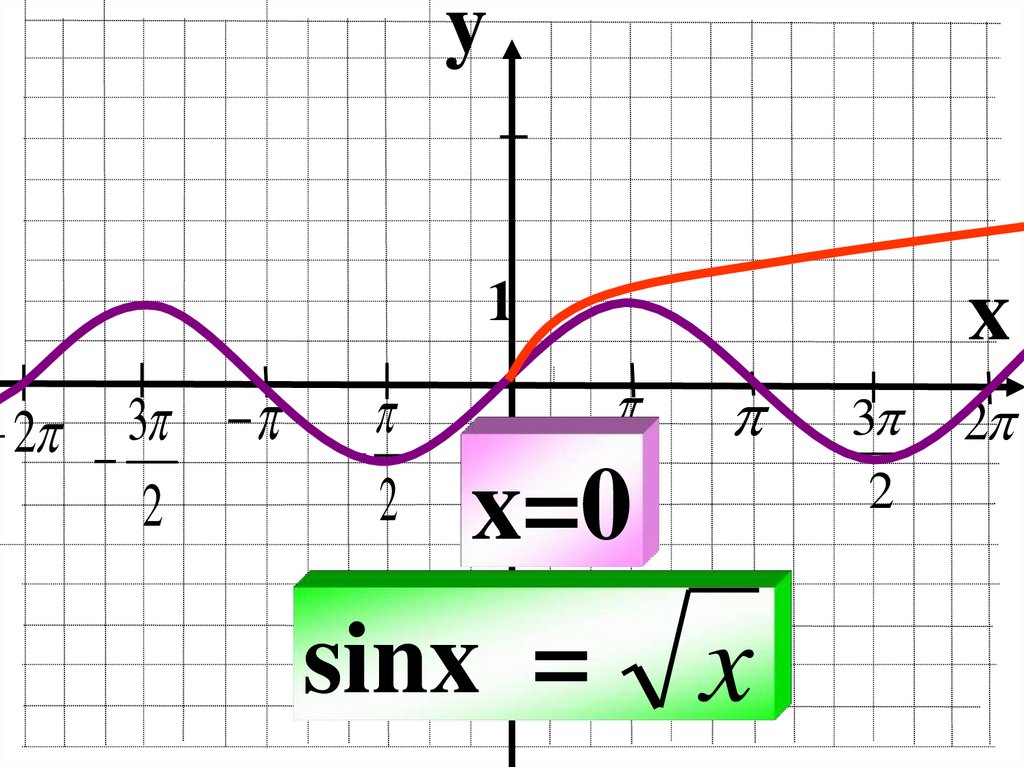
x=0
sinx = x
3
2
2

14.

y
Ø
2
2
3
2
1
-1
2
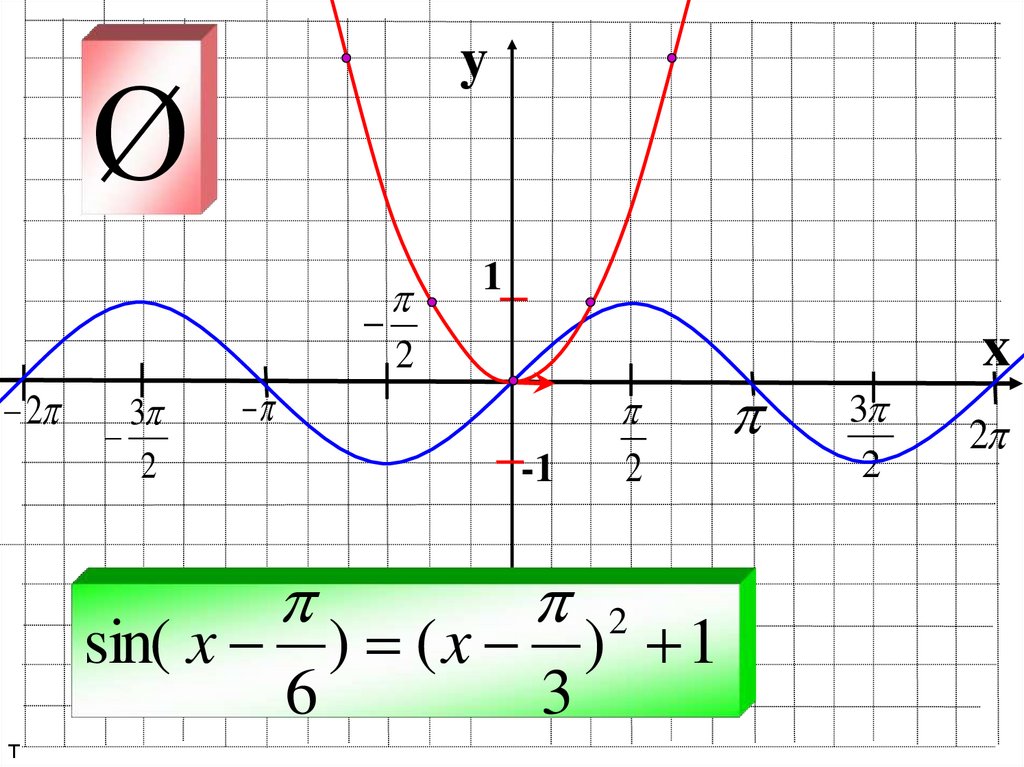
sin( x ) = ( x ) 1
6
3
т
2
x
3
2
2

15.

y
Ø
2 3
2
x
1
2
-1
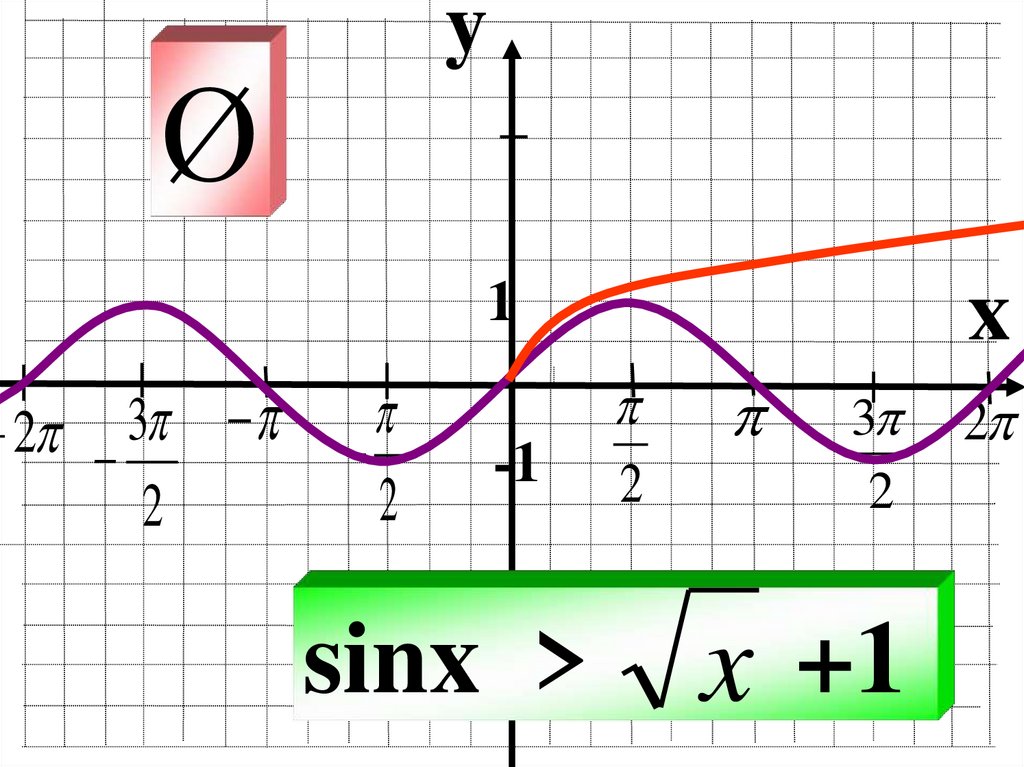
sinx >
2
3
2
x +1
2

16.

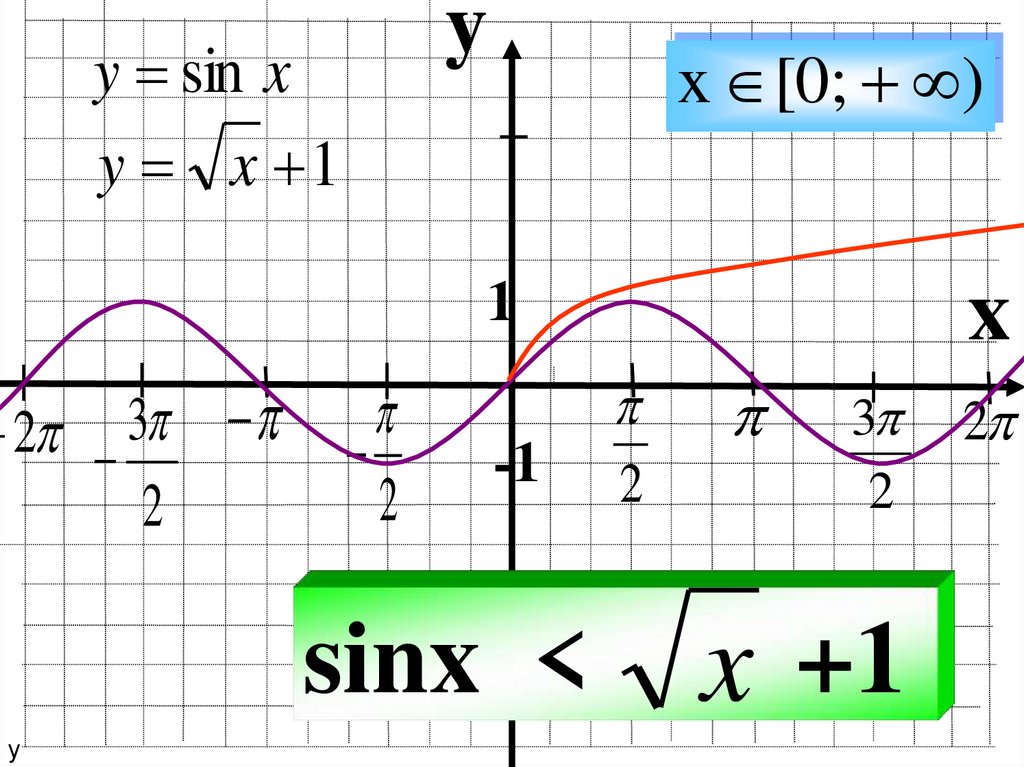
y
y = sin x
y = x 1
x [0; )
x
1
2 3
2
2
-1
sinx <
у
2
3
2
x +1
2

17.

2
1
sin(x
)<–
3
2
5
6
2
2
т
3
2
y
1
7
6
-1
2
x
3
2
2

18.

y
I
I
3
2
2
I
I
-1
2
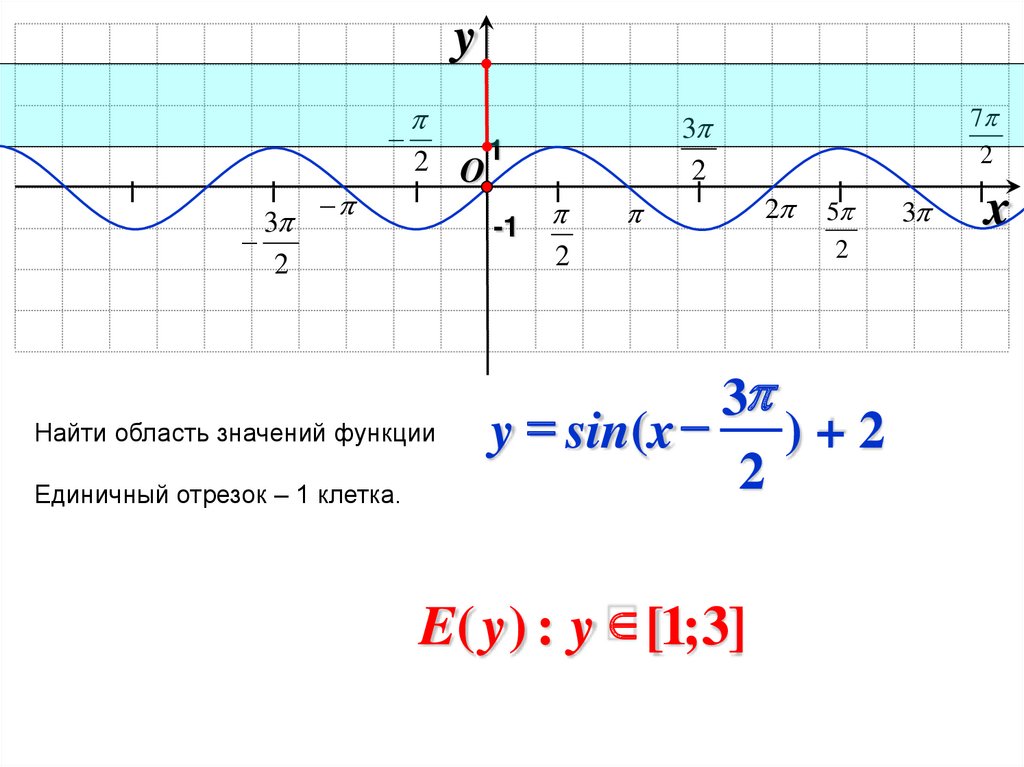
Найти область значений функции
Единичный отрезок – 1 клетка.
O
1
3
2
I
7
2
2
I
5
2
3
y = sin(x ) + 2
2
E( y ) : y [1;3]
3
I
x

19.

Умение строить графики нам нужны при …
решении уравнений;
решении неравенств;
решении заданий, связанных с исследованием
свойств функций.
Рассмотрим графики функций, аналитическая запись
которых содержит знак абсолютной величины.

20.

y = sin x
2 3
2
y
x
1
2
-1
2
3
2
2

21.

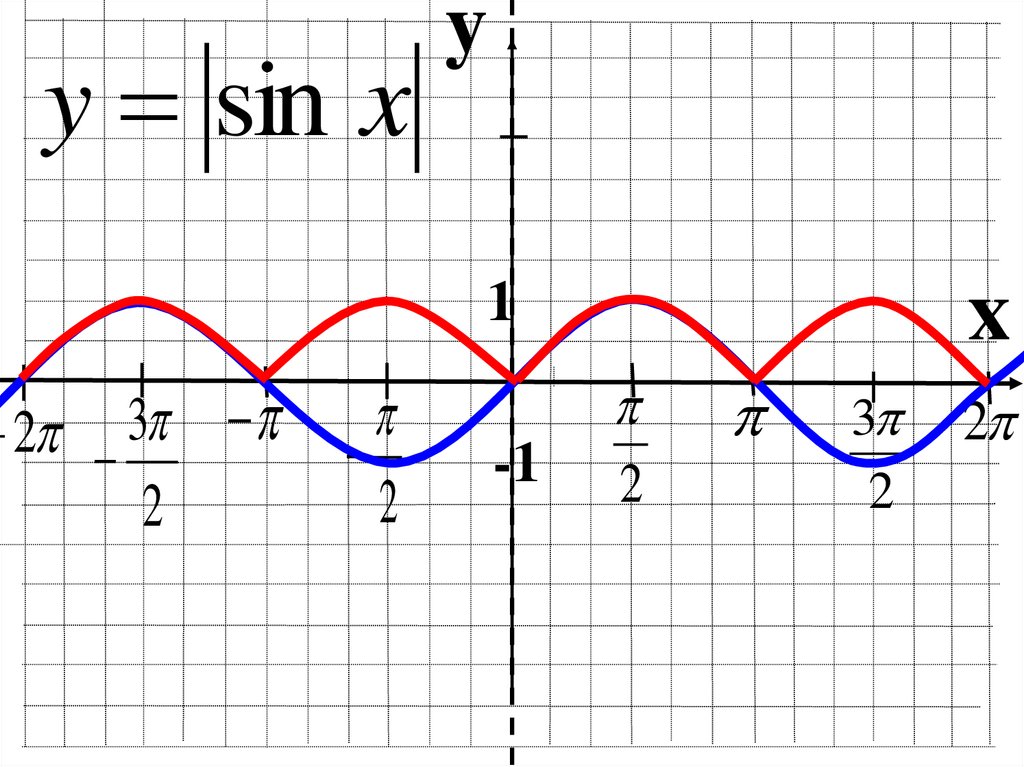
y
y = sin x
2 3
2
x
1
2
-1
2
3
2
2