Производные элементарных функций

1. Производные элементарных функций

2.

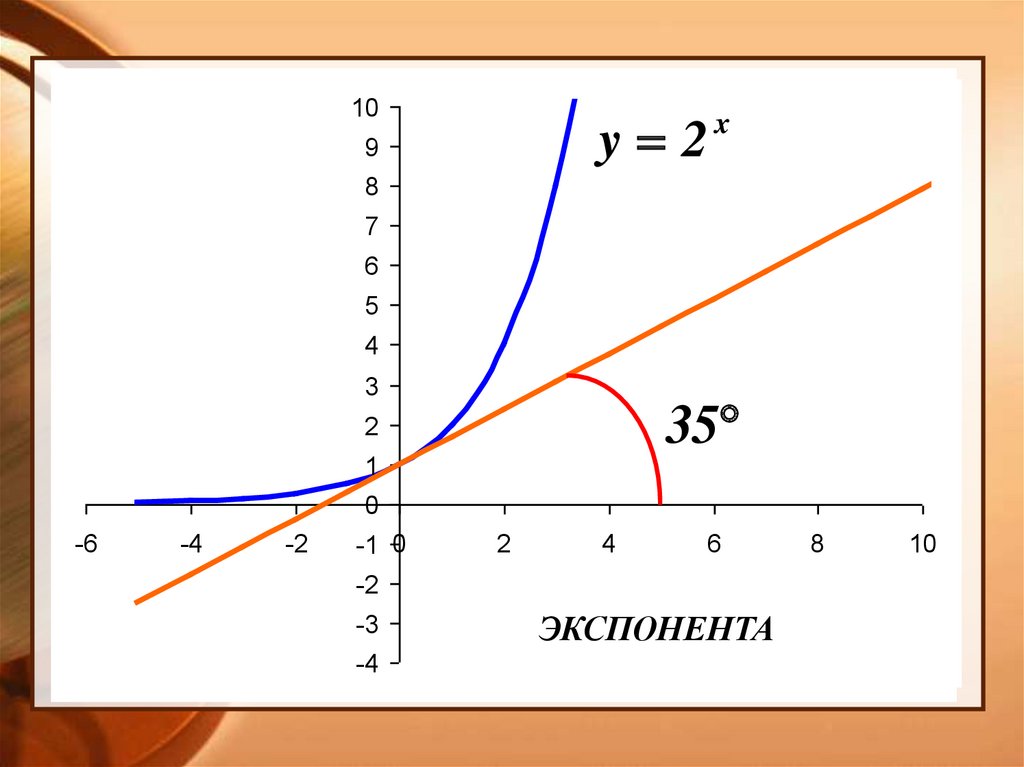
10
y 2
9
x
8
7
6
5
4
3
35
2
1
0
-6
-4
-2
-1 0
2
4
6
-2
-3
-4
ЭКСПОНЕНТА
8
10

3.

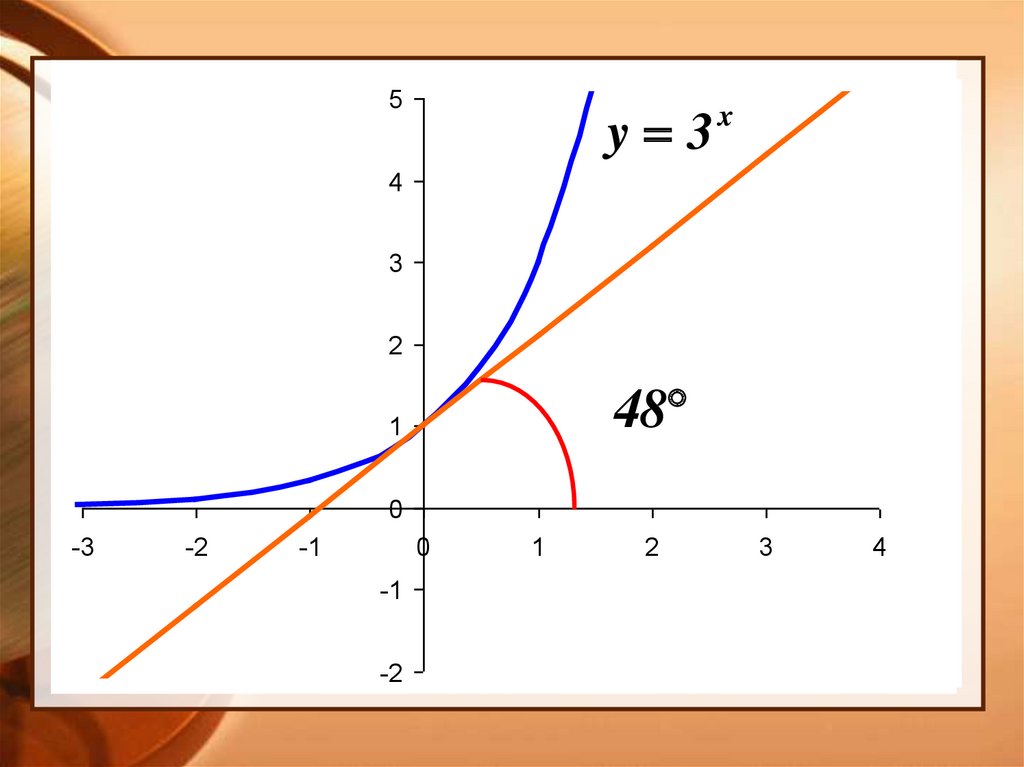
5
y 3
x
4
3
2
48
1
0
-3
-2
-1
0
-1
-2
1
2
3
4

4.

10
y 2
9
5
x
8
y 3x
4
7
6
3
5
4
2
3
35
2
1
-6
-4
-2
0
-1 0
-2
-3
-4
2
4
6
48
1
8
-3 10
0
-2
-1
0
1
2
3
-1
-2
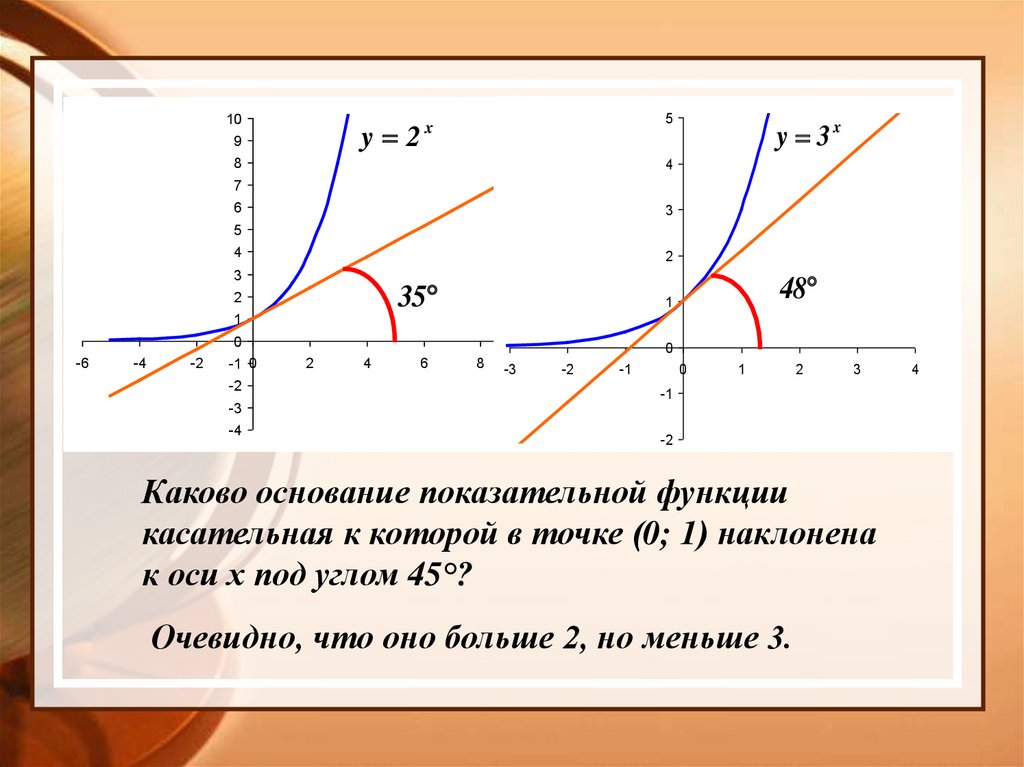
Каково основание показательной функции
касательная к которой в точке (0; 1) наклонена
к оси х под углом 45°?
Очевидно, что оно больше 2, но меньше 3.
4

5.

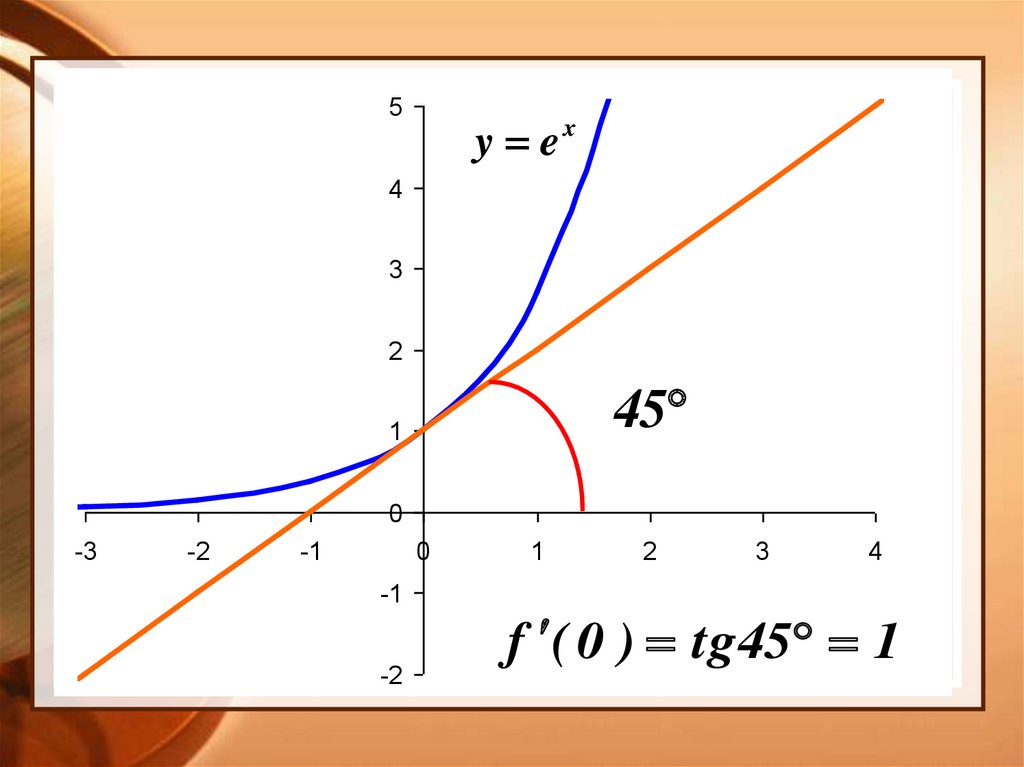
5
y ex
4
3
2
45
1
0
-3
-2
-1
0
-1
-2
1
2
3
4
f ( 0 ) tg45 1

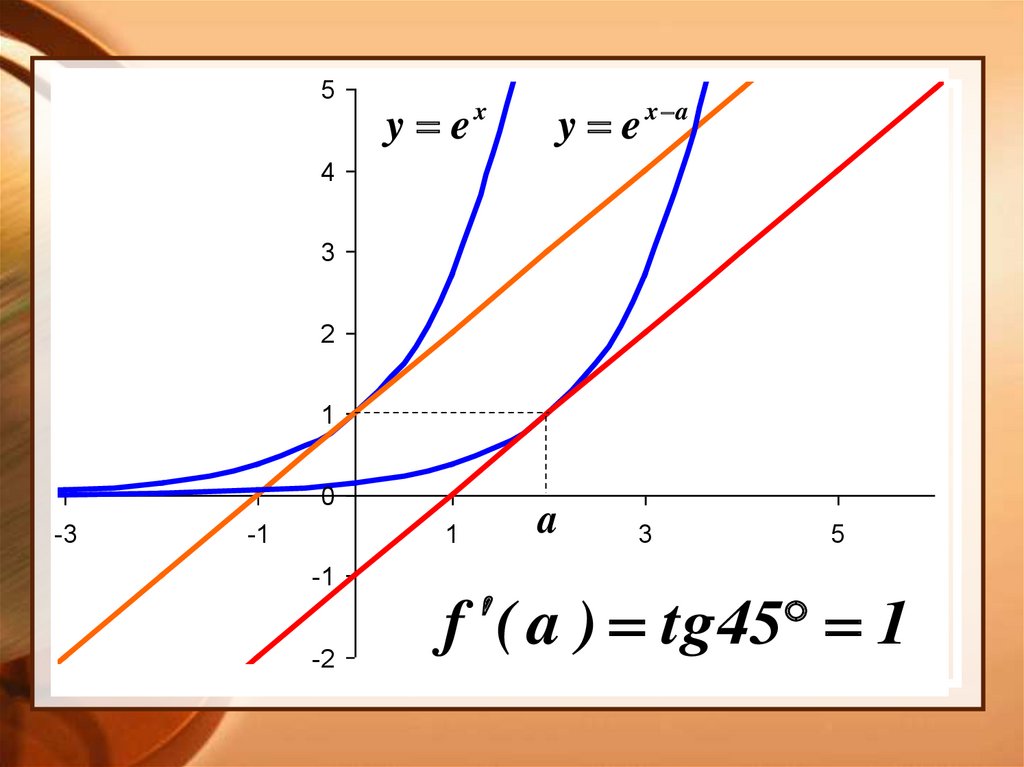
6.

5
y ex
y e x a
4
3
2
1
0
-3
-1
1
-1
-2
a
3
5
f ( a ) tg45 1

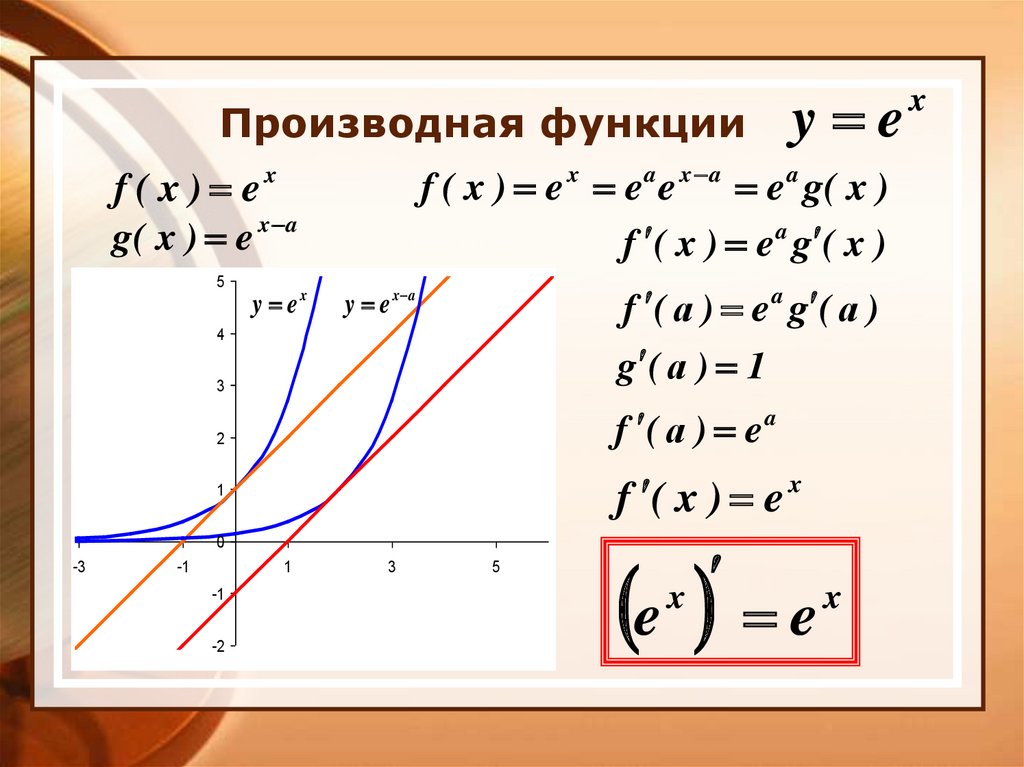
7. Производная функции

f ( x ) e x e a e x a e a g( x )
f ( x ) e a g ( x )
f ( x ) ex
x a
g( x ) e
5
3
f ( а ) e a g ( а )
g ( а ) 1
2
f ( а ) e a
y ex
y e x a
4
f ( x ) e x
1
0
-3
y e
1
-1
-1
-2
3
5
e e
x
x
x

8.

Производная функции
y a
x
a e
x
x ln a
a e
x lna
x
x ln a
a e ln a ae
ln a
a ln a a
x
x

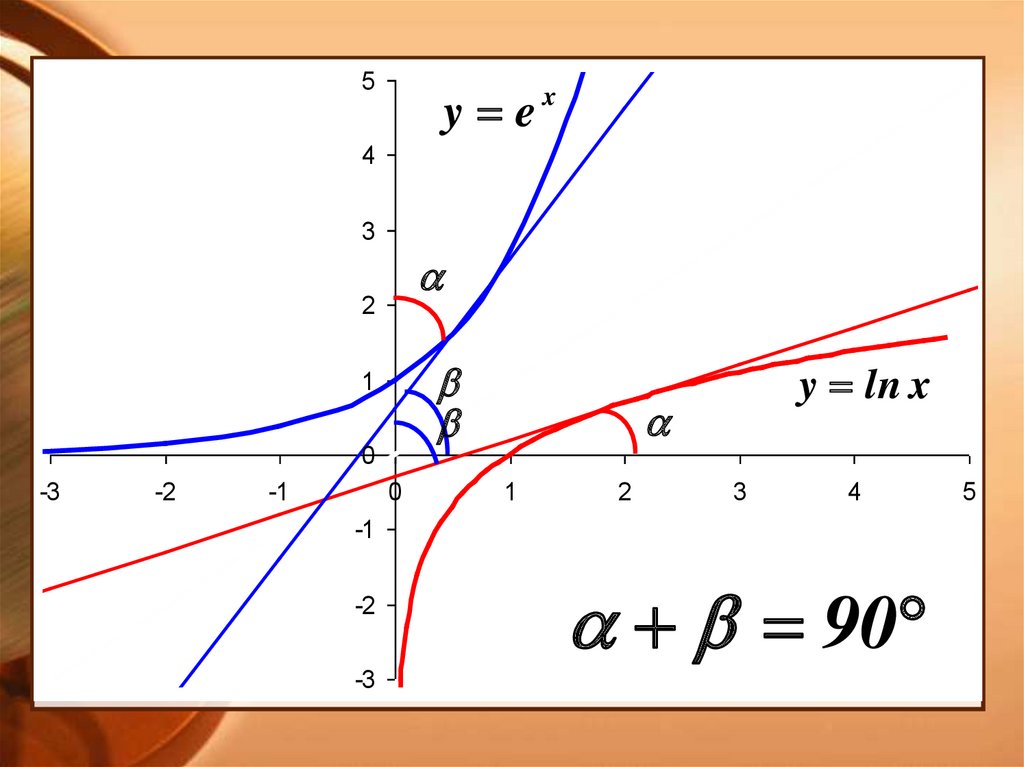
9.

5
y e
x
4
3
2
1
0
-3
-2
-1
0
y ln x
1
2
3
4
-1
-2
-3
90
5

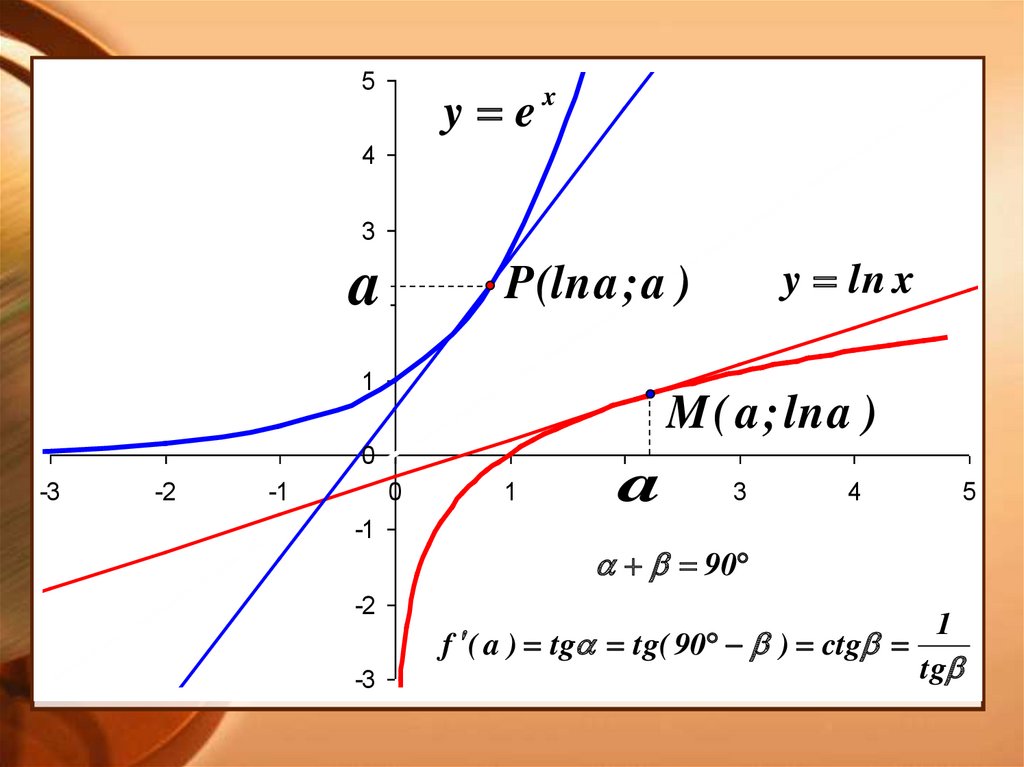
10.

5
y e
x
4
3
a
2
1
M ( a ; ln a )
0
-3
-2
-1
0
-1
y ln x
P (ln a ; a )
1
a
2
3
4
90
-2
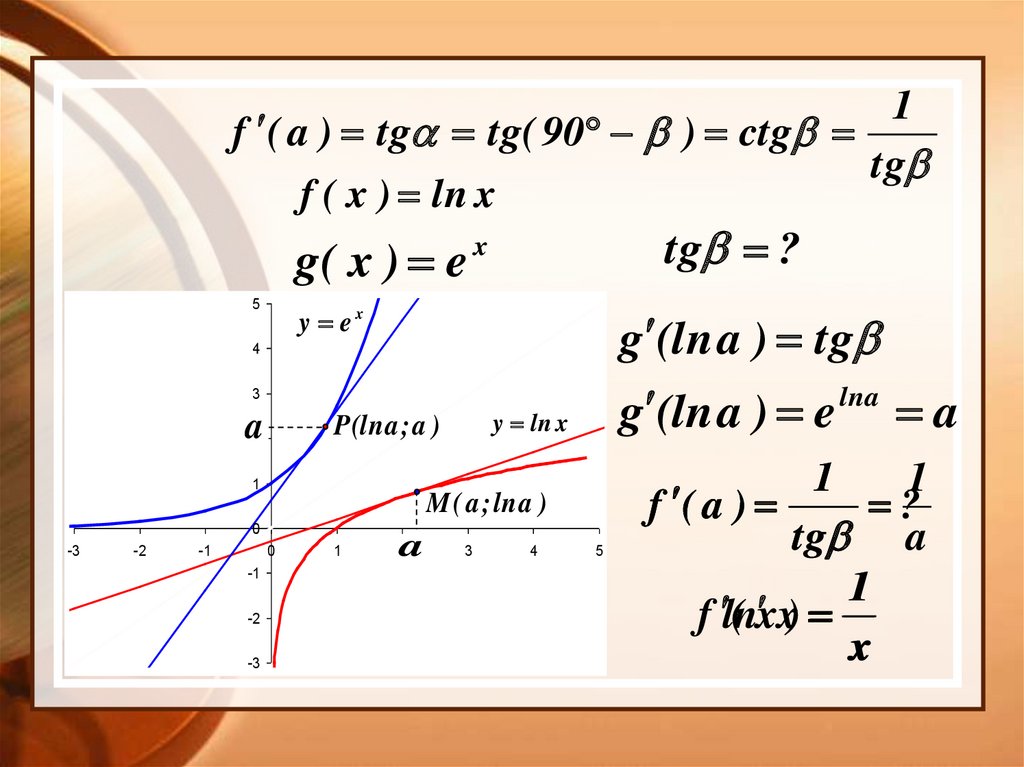
f ( a ) tg tg( 90 ) ctg
-3
5
1
tg

11.

1
f ( a ) tg tg( 90 ) ctg
tg
f ( x ) ln x
g( x ) e
5
tg ?
x
y ex
g (ln a ) tg
lna
g (ln a ) e a
4
3
a
y ln x
P (ln a ; a )
2
1
M ( a ; ln a )
0
-3
-2
-1
0
-1
-2
-3
1
a
2
3
4
5
1
1
f ( a )
?
tg a
1
f l(nx x)
x

12.

1
ln x
x
1
loga x
х ln a
ln x
loga x
ln a
ln x
loga x
ln a
1
1 1
1
ln x
ln a
ln a x x ln a

13.

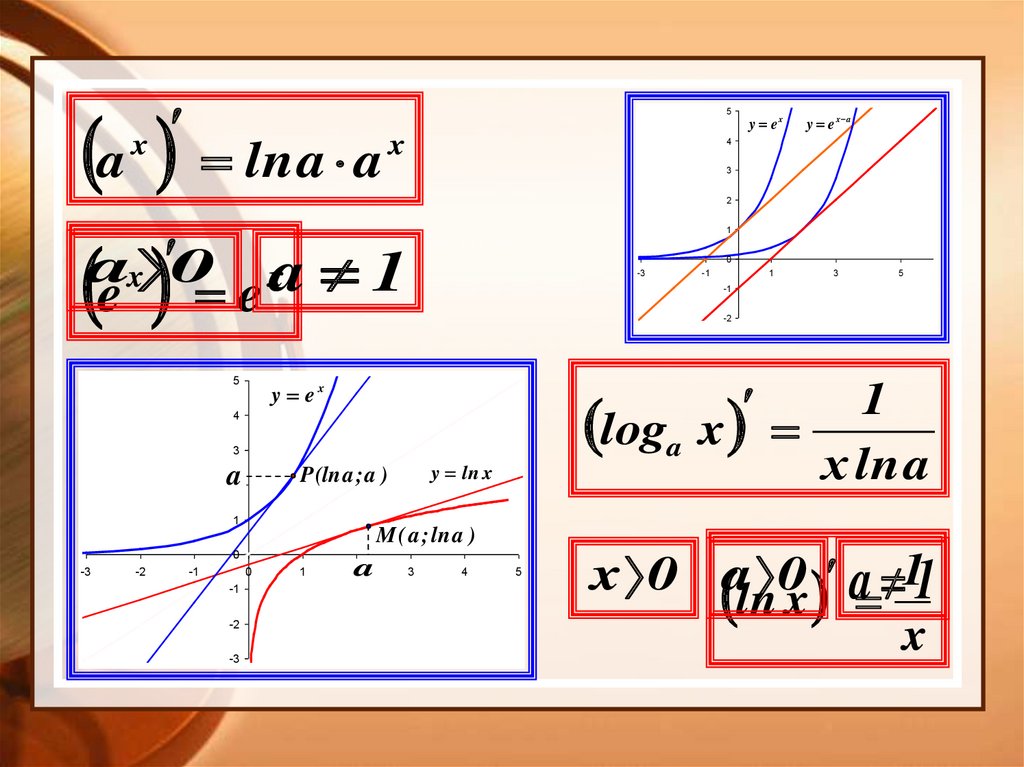
a
x
5
ln a a
x
y ex
y e x a
4
3
2
a
x 0
e
1
ea 1
0
x
5
-3
1
3
5
-1
-2
loga x
y ex
4
3
a2
-1
y ln x
P (ln a ; a )
1
х ln a
1
M ( a ; ln a )
0
-3
-2
-1
0
-1
-2
-3
1
a
2
3
4
5
x 0 a 0 a 11
ln x
x

14.

e
3x
3e
e 2e
2 x
x
2 x
e 2 xe x 2
x2
e
3 5 x
e e
3x
3 5 x
5
e
x

15.

e e a ln a a
x
x
x
a 0
2 2
x
x
a 1
ln 2
5 3 5
3 x
3 x
x
ln 5

16.

loga x
1
ln x
x
1
х ln a
x 0 a 0
1
1
ln 2 x 2
2x x
log
0 ,3
1
x
x ln 0 ,3
a 1

17.

Вариант II
Вариант I
f ( x ) 3e 3
x
f( x) e
2 x
f ( x ) xe
f ( x ) 2 2e
x
x
0 ,5
x
0 ,2 x
f ( x ) x 2 e 2 x 1
1 2 x 2
x2
2
x
f( x) x
e
f ( x ) sin e
f( x) e
x2 x
x
e
f( x) 2
x
x
2
2 x x2
f ( x ) cos e
x2 x
3
2 x 1

18.

Вариант I
f ( x ) 3e 3
x
f ( x ) xe
2
f ( x) e
e
1 2 x 2
x
x
3e
0 ,5
1 2 x 2
x
e
3 x ln 3
e2 x
x
0 ,5 ln 0 ,5
x
x
1 2 x 2
2 1 2 x 2
4x e
1 4 x
2
x
f ( x ) x
e
2
2 xe x x 2 e x 2 x x 2
2x
x
e
e

19.

Вариант II
f ( x ) 2 2e
x
x
2
x
ln 2 2e x
f ( x ) e
0 ,2
( 2 x 1 )e
x
0 ,2 ln 0 ,2
2 2 x 1
2 x 1
2 2 x 1
f ( x ) x e
2 xe
2x e
2 xe 2 x 1 ( 1 x )
x2 x
e
f ( x ) 2
x
x2
x
x2 x
2 xe x 2 x 2 2 xe x 2 2 xe x 2 ( x 2 1 )
4
4
x
x
x2
2
2e ( x 1 )
x3

20.

f ( x ) sin e
cos e
x
e
cos e x e
2 x
x
x
x
sin e
sin e
x x
2
2 x
( 2 2 x ) 2
( 2 2 x ) 2
f ( x ) cos e
x2 x
2
1
2 x x2
x2 x
e
x2 x
e
x x
2
3
2 x x2
2 x 1
2 x x2
ln 2
ln 2
( 2x 1 ) 3
( 2x 1)
3
2 x 1
1
2 ln 3
2 2x 1
2 x 1
ln 3
2x 1