Similar presentations:
Производная и дифференциал. Вычисление производной путем логарифмирования
1. Производная и дифференциал.
2. Вычисление производной путем логарифмирования.
u• Функцию вида y u x
называют
показательно-степенной
сложной показательной функцией.
v( x)
v
или
3.
y uv
ln y ln u
v
ln y v ln u
ln y
v ln u
y
v ln u v ln u
y
4.
yu
v ln u v
y
u
u
y y v ln u v
u
u
y u v ln u v
u
v
5.
1. Продифференцировать функцию:y x
x
ln y ln x
y
1
ln x x
y
x
x
ln y x ln x
y x
x
ln y x ln x
y
x ln x x ln x
y
y
ln x 1
y
y y 1 ln x
y x x 1 ln x
6.
2. Продифференцировать функцию:ln y ln 3
x x2 1
x 1 2
x x2 1
ln y ln
2
x
1
1
3
1 x x2 1
ln y ln
2
3
x 1
y 3
x x2 1
2
x 1
7.
12
2
ln y ln x ln x 1 ln x 1
3
1
ln y ln x ln x 2 1 2 ln x 1
3
1
2
ln y ln x ln x 1 2 ln x 1
3
2
y 1 1 x 1
2 x 1
2
y 3 x
x 1
x 1
8.
y 1 12x
2
2
y 3 x x 1 x 1
1 1
2x
2
y y 2
3 x x 1 x 1
1
1 x x 1
Ответ: y 3
2
3
x 1
2
x
2x
2
2
x 1 x 1
9.
3. Продифференцировать функцию:sin x
y
y log sin x tan x
tan x
ln sin x ln tan x
y
y ln sin x ln tan x
ln tan x
y
ln sin x
10.
ln tan xy
ln sin x
ln tan x ln sin x ln tan x ln sin x
y
2
ln sin x
tan x
y tan x
sin x
ln sin x ln tan x
2
ln sin x
sin x
11.
1cos x ln tan x
ln sin x
2
2
sin x
ln sin x tan x cos x
1
cos x ln tan x
ln sin x
2
sin x
ln sin x sin x cos x
1
ln sin x cos 2 x ln tan x
2
sin x cos x
ln sin x
12.
1ln sin x cos x ln tan x
2
1
ln sin x
sin 2 x
2
2
2 ln sin x cos x ln tan x
2
sin 2 x ln sin x
2
13. Производная неявной функции.
явная функцияy=f(x)
неявная функция
y-f(x)=0 или F(x,y)=0
1
y 1
x
xy x 1 0
y x 2
y x 2
2
2
xy3 x sin y
14.
Пустьxy x 1 0
xy x 1
0
x y xy x 1 0
y xy 1 0
xy 1 y
1 y
y
x
1 x 1
y
1
x
x
1
1
y 1 2
x
x
15.
1 yy
x
y
1
1
y 1 2
x
x
1
1
x
1
1 1
1 y
1
x
y
2
x
x
x
16.
4. Продифференцировать функцию:xy
3
xy x sin y
3
x sin y
x y x y
3
3
x sin y
y x 3 y y 1 y cos y
3
3 y
2
2
x cos y y 1 y 3
Ответ:
1 y 3
1 y3
y 2
2
3 y x cos y
3 y x cos y
17. Производная функции, заданная параметрически.
Пустьx x(t )
y y (t )
t (x ) - обратная для функции
x x(t )
Тогда функцию y=f(x) можно рассматривать как
сложную функцию: y
y (x) , т.е y y t , t ( x)
где t- промежуточный аргумент.
18.
По правилу дифференцирования сложной функции,получим:
1
1 yt
y x yt t x t x yt
x
x
x
t
t
t
теорема о дифференцировании
обратной функции
yt
y x
xt
19. Пример: найти , если
Пример: найти y x , если1
xt ln t
t
x ln t
y arctan t
1
yt arctan t
2
1 t
yt
1
1
t
y x
:
2
2
xt 1 t t 1 t
Ответ:
t
y x
1 t2










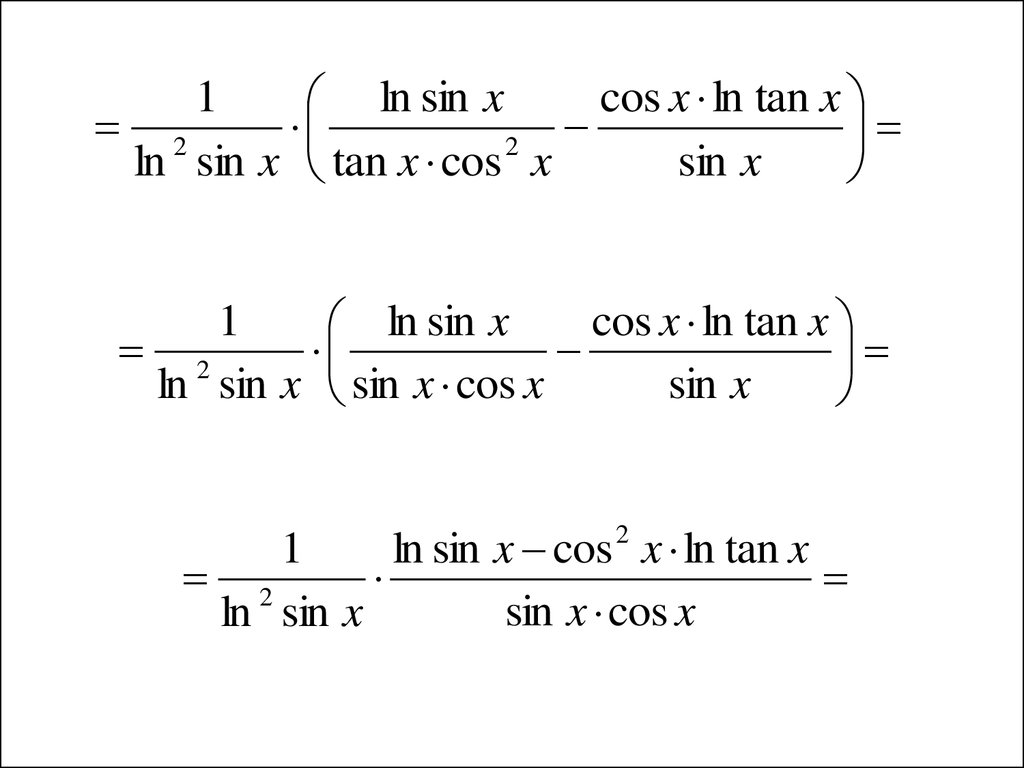








 mathematics
mathematics








