Сложное движение точки и твердого тела. Изучить лекцию и написать конспект

1. РАЗДЕЛ КИНЕМАТИКА

Тема 2.3
Сложное движение точки
и твердого тела
Изучить лекцию и написать конспект

2. 1. Сложное движение точки

Понятие сложного
движения.
Основные
определения
сложного движения
точки.
Понятие относительного
движения.
Понятие переносного
движения.
Понятие абсолютного
движение.
Кинематические
характеристики
точки при ее
сложном движении.
Определение скорости.
Определение ускорения
точки.

3.

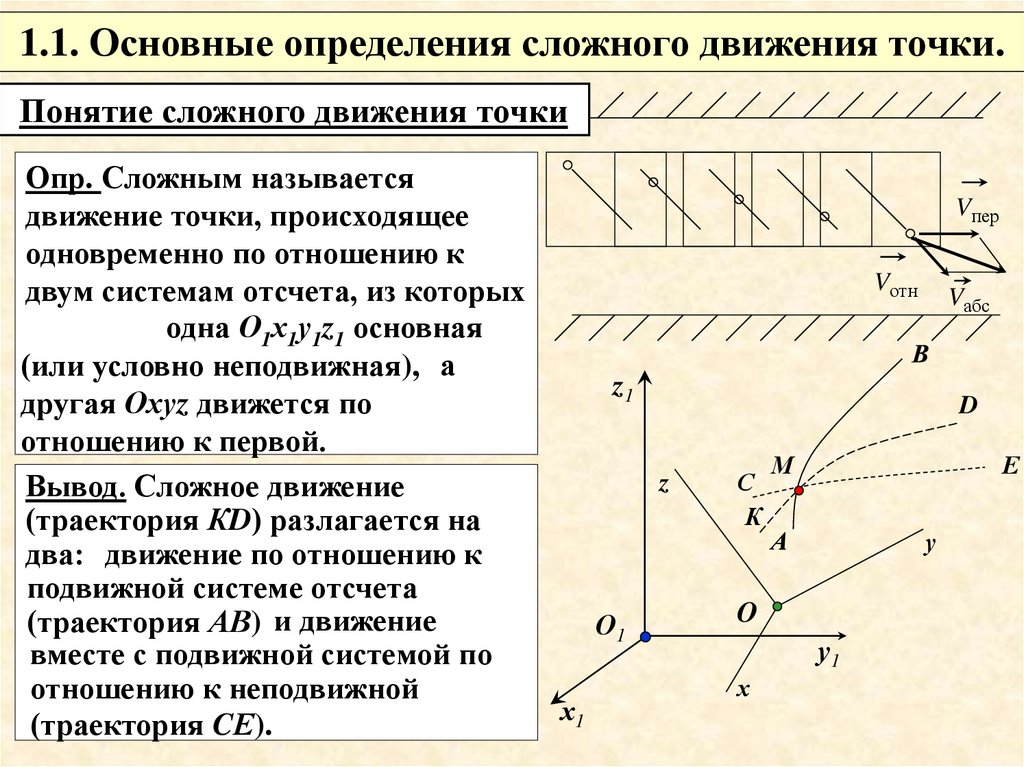
1.1. Основные определения сложного движения точки.
Понятие сложного движения точки
Опр. Сложным называется
движение точки, происходящее
одновременно по отношению к
двум системам отсчета, из которых
одна О1х1у1z1 основная
(или условно неподвижная), а
другая Охуz движется по
отношению к первой.
Вывод. Сложное движение
(траектория КD) разлагается на
два: движение по отношению к
подвижной системе отсчета
(траектория АВ) и движение
вместе с подвижной системой по
отношению к неподвижной
(траектория CЕ).
Vпер
Vотн
Vабс
z1
D
z
О1
х1
С
К
М
Е
у
O
у1
х

4.

Понятие относительного движения точки
Опр. Движение, совершаемое точкой
М по отношению к подвижной
системой отсчета Охуz, называется
относительным движением.
Опр. Траектория АВ,
описываемая точкой в
относительном движении (по
отношению к подвижной системе
отсчета Охуz), называется
относительной траекторией.
z1
z
D
М
С
Е
К
О1
х1
Vr
у
O
у1
х
Опр. Скорость точки М по отношению к осям
Охуz
называется относительной скоростью (Vотн или Vr ) , а
ускорение точки М по отношению к осям Охуz называется
относительным ускорением (аотн или аr ).

5.

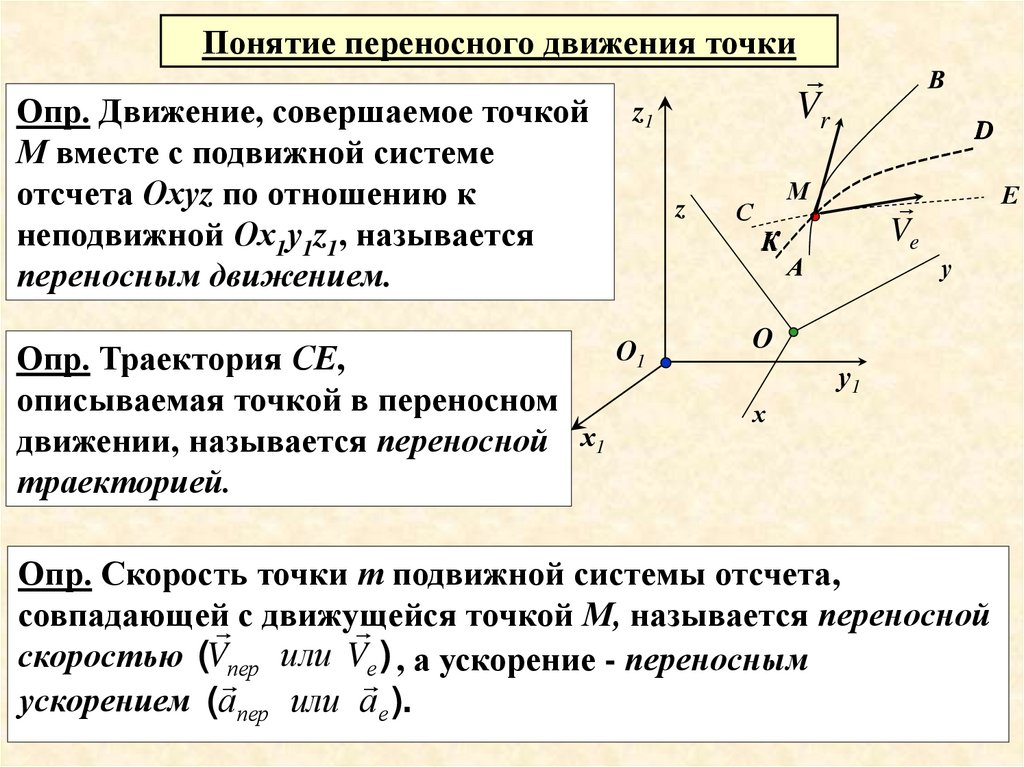
Понятие переносного движения точки
Опр. Движение, совершаемое точкой
М вместе с подвижной системе
отсчета Охуz по отношению к
неподвижной Ох1у1z1, называется
переносным движением.
Vr
z1
О1
Опр. Траектория СЕ,
описываемая точкой в переносном
движении, называется переносной х1
траекторией.
z
D
М
С
Ve
К
Е
у
O
у1
х
Опр. Скорость точки т подвижной системы отсчета,
совпадающей с движущейся
точкой М, называется переносной
скоростью (Vпер или Vе ) , а ускорение - переносным
ускорением (апер или ае ).

6.

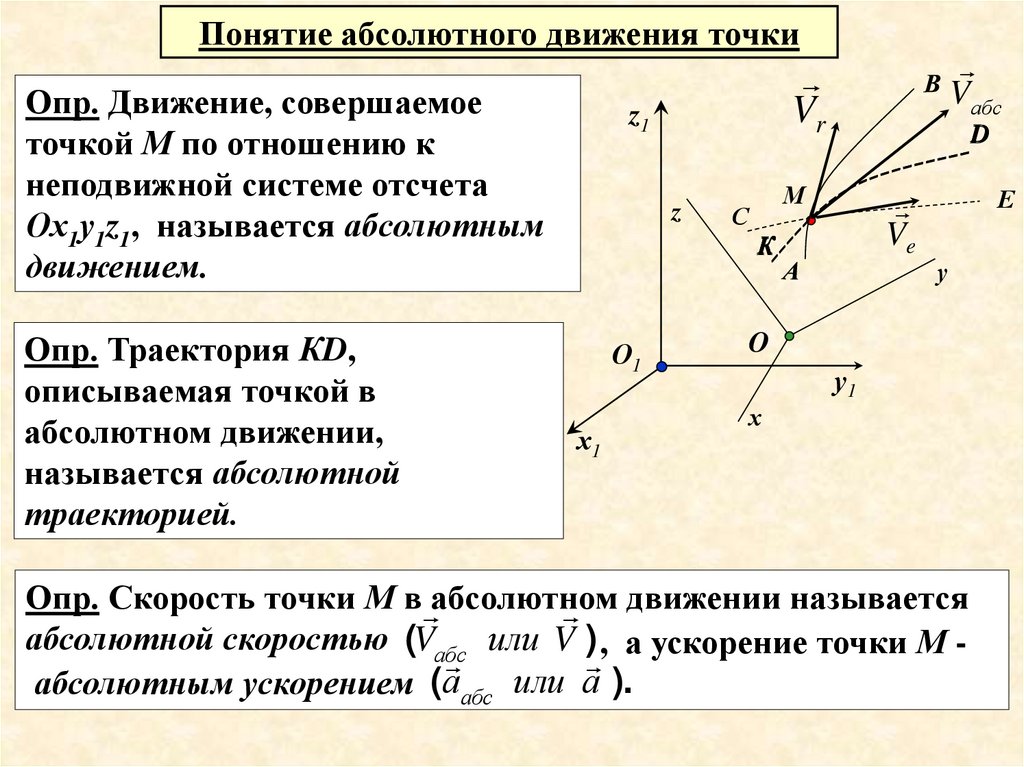
Понятие абсолютного движения точки
Опр. Движение, совершаемое
точкой М по отношению к
неподвижной системе отсчета
Ох1у1z1, называется абсолютным
движением.
Опр. Траектория КD,
описываемая точкой в
абсолютном движении,
называется абсолютной
траекторией.
Vабс
Vr
z1
z
D
М
С
Ve
К
О1
х1
Е
у
O
у1
х
Опр. Скорость точки М в абсолютном
движении называется
абсолютной скоростью (Vабс или V ) , а ускорение точки М
абсолютным ускорением (аабс или а ).

7.

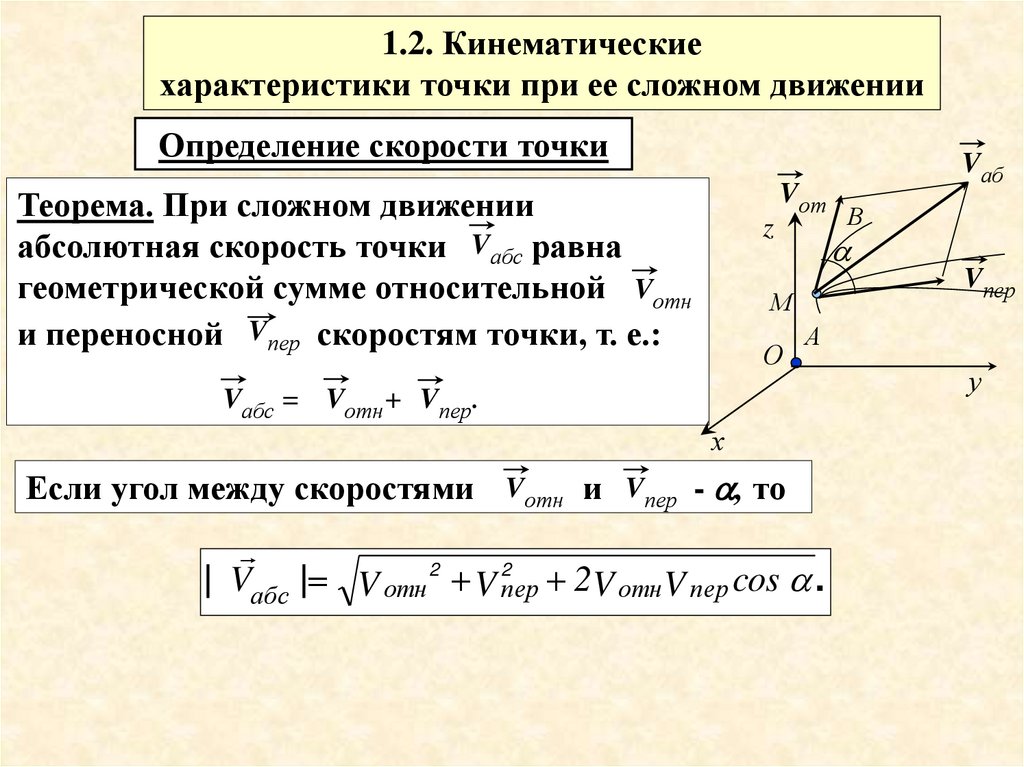
1.2. Кинематические
характеристики точки при ее сложном движении
Определение скорости точки
Теорема. При сложном движении
абсолютная скорость точки Vабс равна
геометрической сумме относительной Vотн
и переносной Vпер скоростям точки, т. е.:
z
Vот
В
М
О
Vаб
Vпер
А
Vабс = Vотн + Vпер.
х
Если угол между скоростями Vотн и Vпер - , то
| Vабс | V отн 2 V 2пер 2V отн V пер cos .
у

8.

Определение ускорения точки
Теорема Кориолиса. При сложном движении ускорение точки
равно
геометрической
сумме
трех
ускорений:
относительного,
переносного
и
поворотного,
или
кориолисова.
где
аабс аотн апер акор ,
аот – относительное ускорение, характеризующее изменение
относительной скорости только при относительном
движении;
апер– переносное ускорение, характеризующее изменение
переносной скорости только при переносном движении;
акор 2 Vотн – кориолисово (поворотное) ускорение,
характеризующее изменение относительной скорости при
переносном движении и переносной скорости точки при ее
относительном движении.

9.

Определение модуля и направления кориолисова ускорения
а) модуль определится по формуле:
акор= 2.| |.|VОТ|. sin .
акор= 0, если
– = 0 (нет переносного вращения);
– вектор относительной скорости Vотn
параллелен оси переносного
0);
вращения
(
=
0
или
=
180
Vотн 0.
Vот
z
х
V Пот
акор
900
П
б) направление вектора ако р определяется по правилу
векторного произведения или по правилу Жуковского:
- проводят плоскость, перпендикулярную вектору угловой
скорости ;
- проектируют вектор Vотn на эту плоскость;
- полученный вектор проекции V Пот поворачивают в
сторону вращения на угол 900.
у

10.

Определение модуля и направления абсолютного
ускорения точки
Модуль и направление абсолютного ускорения точки
определяются по методу проекций:
аабс аотн апер акор ,
аабcХ = аотнХ + аперХ + акорХ ,
аабcУ = аотнУ + аперУ + акорУ ,
| аабс | аабсx 2 а2абсу аабсz 2 ,
аабcZ = аотнZ + аперZ + акорZ .
соs аабсx / | а |, сos аабсу / | а |, cos аабсz / | а | .
Теорема о сложении ускорений в случае поступательного
переносного движения
Теорема. При поступательном переносном движении
абсолютное ускорение точки равно геометрической сумме
относительного и переносного ускорений
аабс аотн апер .

11.

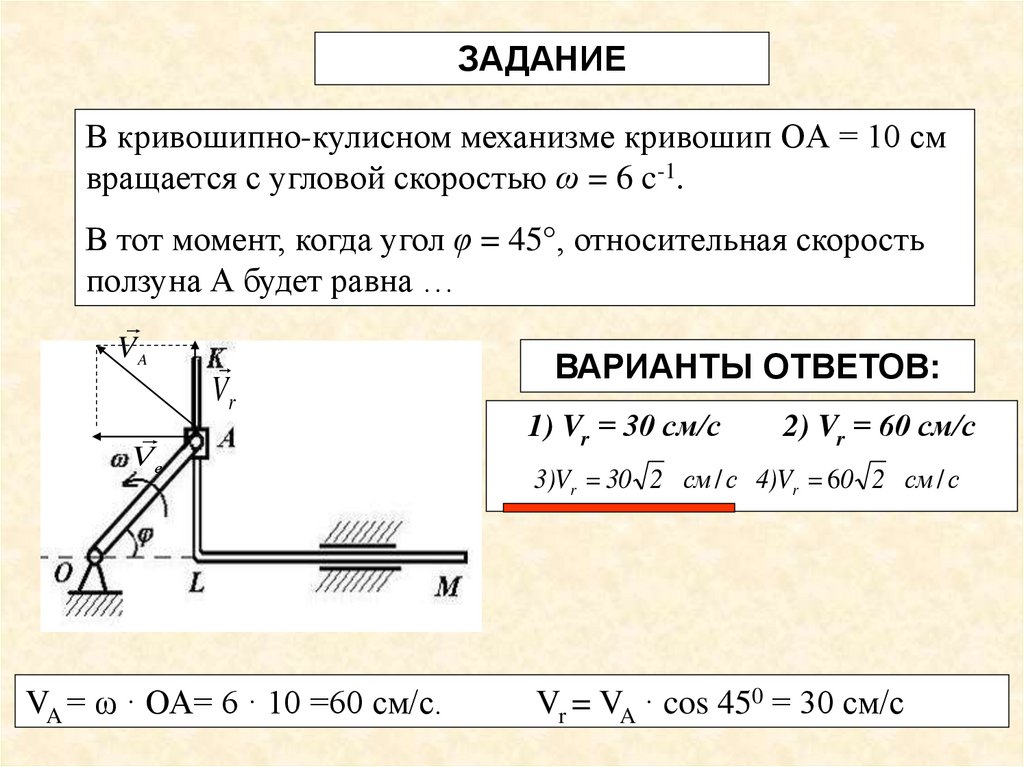
ЗАДАНИЕ
В кривошипно-кулисном механизме кривошип OА = 10 см
вращается с угловой скоростью ω = 6 c-1.
В тот момент, когда угол φ = 45°, относительная скорость
ползуна А будет равна …
VA
Vr
Vе
VA = ω · ОА= 6 · 10 =60 см/с.
ВАРИАНТЫ ОТВЕТОВ:
1) Vr = 30 см/с
2) Vr = 60 см/с
3)Vr 30 2 см / с 4)Vr 60 2 см / с
Vr = VA · cos 450 = 30 см/с

12.

ЗАДАНИЕ
Прямоугольная пластинка вращается вокруг вертикальной
оси по закону φ = π t/3 рад. По одной из сторон пластинки
движется точка по закону ОМ = 2 t м.
Ускорение Кориолиса для точки М, равно…
ВАРИАНТЫ ОТВЕТОВ:
е
| акор |
Vr
1) 2π/3 м/с2
2) 0 м/с2
3) 2πt/3 м/с2
4) 2π 3 /3 м / с 2
2 | | | Vотн | sin( ,Vотн ) 2 | | | Vотн | sin(180 0 ) 0.

13.

2. Сложение движение тела
Опр. Движение тела называется
сложным , если оно движется
относительно подвижных Охуz, а эти
оси совершают переносное движение
по отношению к неподвижным осям
О1х1у1z1.
z1
z
у
О
О1
х
у1
х1
Сложение поступательных движений
Пусть относительное
движение является поступательным со
скоростью V1 , а переносное движение – тоже поступательное
со скоростью V2 .
Тогда все точки
тела в относительном движении
будут иметь
скорость V1 , а в переносном – скорость V2 .

14.

По теореме о сложении скоростей все точки тела в
абсолютном
движении имеют одну и ту же скорость
V V1 V2 , т.е. абсолютное движение тела будет тоже
поступательным.
Вывод. При сложении
двух поступательных движений со
скоростями V V1 и V2 результирующее
также
движение
будет поступательным со скоростью V V1 V2 .
Сложение вращений вокруг двух параллельных осей
Рассмотрим случай, когда
относительное движение тела
является вращением с угловой
скоростью 1 вокруг оси аа/,
укрепленной на оси bа, а переносное
– вращением кривошипа bа вокруг
/, с угловой
оси bb/, параллельной
аа
скоростью 2 .
b/
2
В
b
а/
1
А
а

15.

Случай 2.1. Вращения направлены в одну сторону
Рассмотрим сечение (S) осям вращения аа/ и bb/. Точки А и
В – следы от осей вращения. Точка А имеет скорость только
за счет вращения вокруг оси Вb/, следовательно, VА = 2 ·АВ.
Точно так же VВ = 1· АВ. М.ц.с. для (S) в точке С.
Угловая скорость (S) - = VА/АС = VВ/ВС.
Откуда = (VА+VВ)/АВ = 1 + 2.
Вывод. При сложении вращений,
направленных в одну сторону,
результирующее движение будет
мгновенным вращением с абсолютной
угловой скоростью = 1 + 2 вокруг
мгновенной оси, параллельной
данным осям.
b
/
а /
2
1
В
С
А
VА
В
VВ
с/
2
А
С
(S)
1

16.

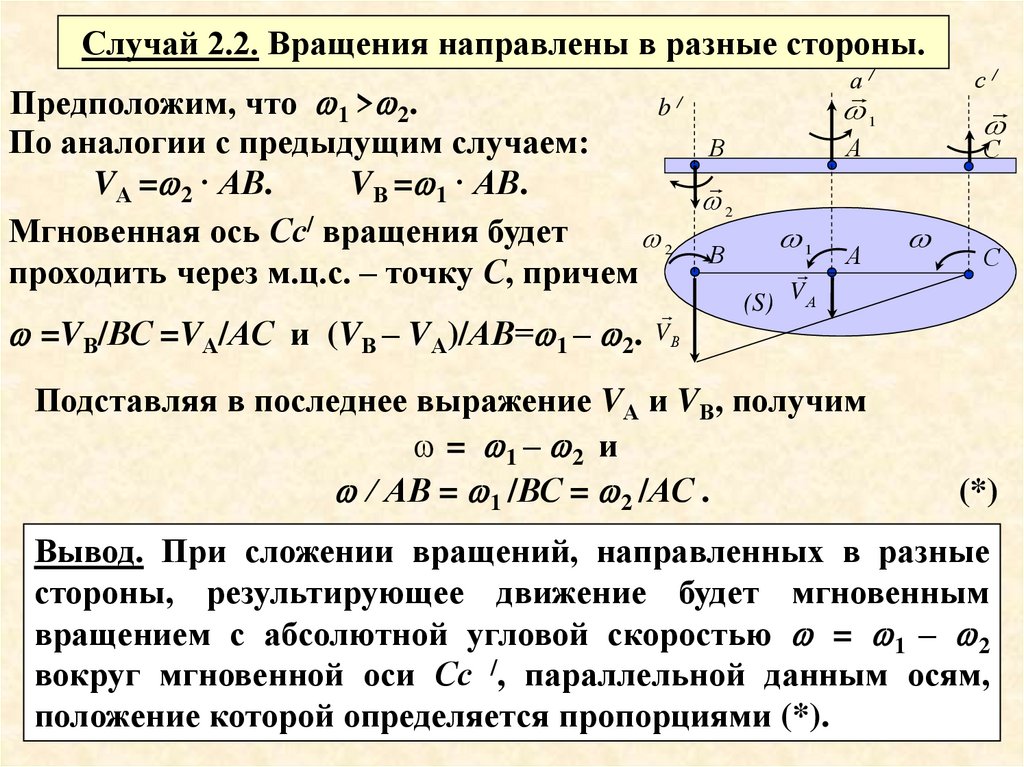
Случай 2.2. Вращения направлены в разные стороны.
Предположим, что 1 > 2.
b/
По аналогии с предыдущим случаем:
В
VА = 2 · АВ.
VВ = 1 · АВ.
2
/
Мгновенная ось Сс вращения будет
2
В
проходить через м.ц.с. – точку С, причем
=VВ/ВС =VА/АС и (VВ – VА)/АВ= 1 – 2.
VВ
а /
с/
А
С
1
1
V
(S) А
А
Подставляя в последнее выражение VА и VВ, получим
= 1 – 2 и
/ АВ = 1 /ВС = 2 /АС .
С
(*)
Вывод. При сложении вращений, направленных в разные
стороны, результирующее движение будет мгновенным
вращением с абсолютной угловой скоростью = 1 – 2
вокруг мгновенной оси Сс /, параллельной данным осям,
положение которой определяется пропорциями (*).

17.

Случай 2.3. Пара вращений
Рассмотрим случай, когда
вращения направлены в разные
стороны , но по модулю 1= 2.
Такая совокупность вращений
называется парой вращений, а
векторы 1 и 2 образуют пару
угловых скоростей.
1
В
А
V
2
VВ
2
1
В
(S)
А
VА
Для скоростей точек А и В: VА = 2 · АВ, VВ = 1 ·АВ, т. е. VА = VВ.
М.ц.с. находится в бесконечности, поэтому скорости всех его
точек равны и численно определяться по формуле: V = 1 · АВ.
Вывод. В случае пары вращения движение тела будет
поступательным со скоростью численно равной 1 · АВ и
направленной
перпендикулярно
плоскости,
проходящей через
векторы 1 и 2 ;направление вектора V определяется так
же, как в статике определяется направление момента пары m.

18.

1 1
2
А
2
О
Сложение вращений вокруг пересекающихся осей
Пусть относительное движение тела
представляет
собой вращение с угловой
скоростью 1 вокруг оси а1а,
укрепленной на кривошипе 2, а
переносным является врашение
кривошипа с угловой скоростью 2
вокруг оси b1 b, которая с осью а1а
пересекается в точке О.
Е
D
Пример. Велосипедная педаль.
а
b
1
О
1
2
а1
b1
2
Скорость точки О равна нулю, т.е. тело 1 совершает
сферическое движение. Угловая скорость тела 1 2 .
V

19.

Вывод. При сложении вокруг двух осей,
пересекающихся
в
точке
О,
результирующее движение тела будет
мгновенным вращением вокруг оси Ос,
проходящей через точку О, и угловая
скорость этого вращения будет равна
геометрической сумме относительной и
переносной угловых скоростей.
с
b
а
2
1
О
Мгновенная ось Ос направлена вдоль вектора , т. е. по
диагонали параллелограмма,
на векторах
построенного
1 и 2 .
Сложение вращений вокруг пересекающихся осей
Переносное движение – движение платформы со скоростью V .
Относительное движение – вращение с угловой скоростью .

20.

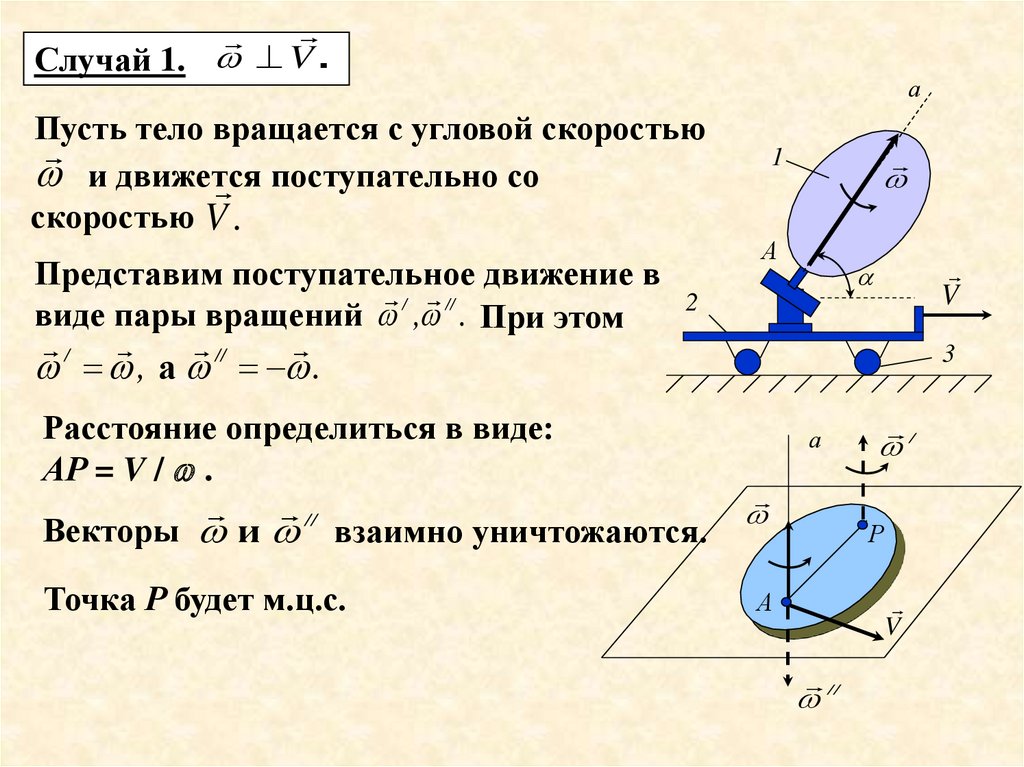
Случай 1. V .
а
Пусть тело вращается с угловой скоростью
и движется
поступательно со
скоростью V .
Представим поступательное движение в
/ //
виде пары вращений , . При этом
1
А
V
2
/
//
, а .
3
Расстояние определиться в виде:
АР = V / .
//
Векторы и
взаимно уничтожаются.
Точка Р будет м.ц.с.
а
/
Р
А
V
//

21.

Случай 2. Винтовое движение (V || ).
Если сложное движение тела
складывается из вращательного
вокруг
оси Аа, с угловой скоростью
и поступательного со скоростью V ,
направленного параллельно оси Аа, то
движение называется винтовым.
Ось Аа называется осью винта.
а
V
М
h
А
Расстояние, проходимое за время одного оборота любой
точкой тела, не лежащей на оси винта, называется шагом h
винта. Можно показать, то h = 2 V / .
V