Сложное движение твердого тела

1.

КИНЕМАТИКА
Сложное движение твердого тела

2.

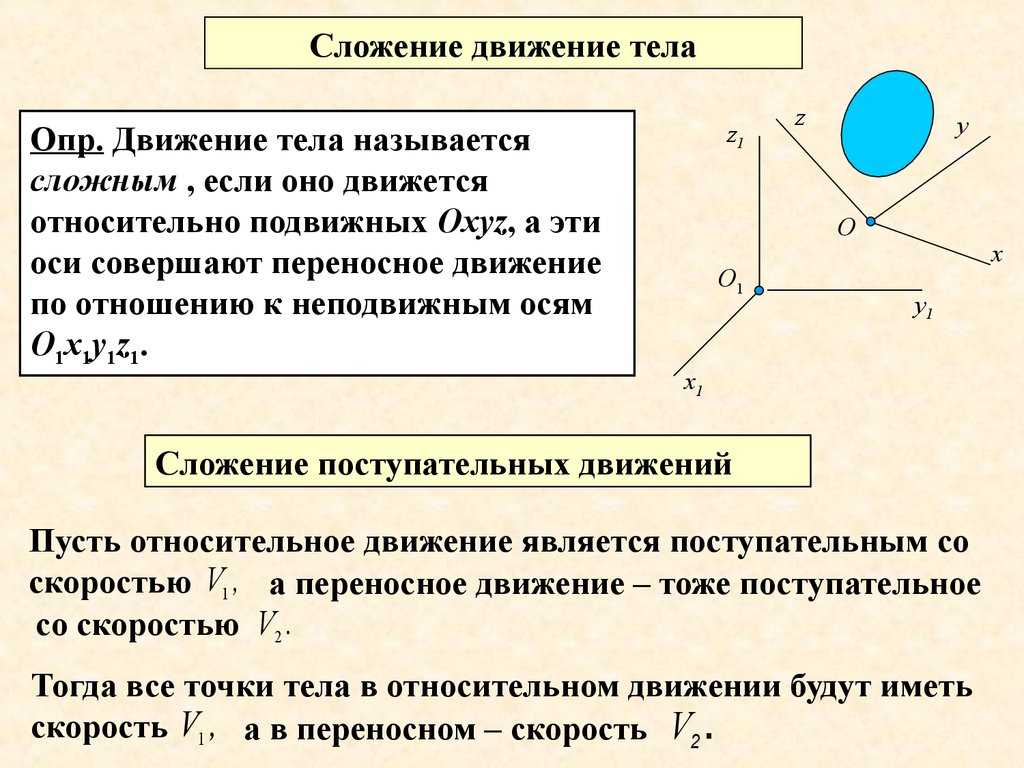
Сложение движение тела
Опр. Движение тела называется
сложным , если оно движется
относительно подвижных Охуz, а эти
оси совершают переносное движение
по отношению к неподвижным осям
О1х1у1z1.
z1
z
у
О
О1
х
у1
х1
Сложение поступательных движений
Пусть относительное
движение является поступательным со
V1 , а переносное движение – тоже поступательное
скоростью
со скоростью V2 .
Тогда все точки
тела в относительном движении
будут иметь
скорость V1 , а в переносном – скорость V2 .

3.

По теореме о сложении скоростей все точки тела в
абсолютном
движении имеют одну и ту же скорость
V V1 V2 , т.е. абсолютное движение тела будет тоже
поступательным.
Вывод. При сложении
двух поступательных движений со
скоростями V V1 и V2 результирующее
также
движение
будет поступательным со скоростью V V1 V2 .
Сложение вращений вокруг двух параллельных осей
Рассмотрим случай, когда
относительное движение тела
является вращением с угловой
скоростью 1 вокруг оси аа/,
укрепленной на оси bа, а переносное
– вращением кривошипа bа вокруг
/
оси bb/, параллельной
аа
, с угловой
скоростью 2 .
b/
2
В
b
а/
1
А
а

4.

Случай 1. Вращения направлены в одну сторону
Рассмотрим сечение (S) осям вращения аа/ и bb/. Точки А и
В – следы от осей вращения. Точка А имеет скорость только
за счет вращения вокруг оси Вb/, следовательно, VА = 2 ·АВ.
Точно так же VВ = 1· АВ. М.ц.с. для (S) в точке С.
Угловая скорость (S) - = VА/АС = VВ/ВС.
Откуда = (VА+VВ)/АВ = 1 + 2.
Вывод. При сложении вращений,
направленных в одну сторону,
результирующее движение будет
мгновенным вращением с абсолютной
угловой скоростью = 1 + 2 вокруг
мгновенной оси, параллельной
данным осям.
b
/
а /
2
1
В
С
А
VА
В
VВ
с/
2
А
С
(S)
1

5.

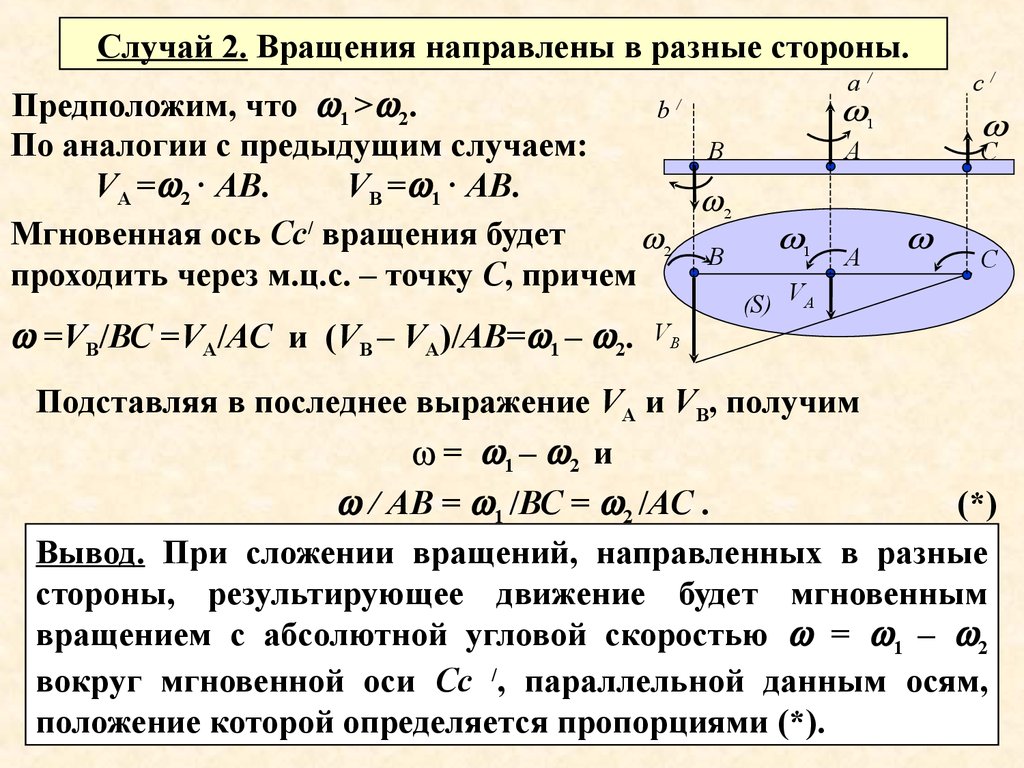
Случай 2. Вращения направлены в разные стороны.
Предположим, что 1 > 2.
b/
По аналогии с предыдущим случаем:
В
VА = 2 · АВ.
VВ = 1 · АВ.
2
Мгновенная ось Сс/ вращения будет
2
В
проходить через м.ц.с. – точку С, причем
=VВ/ВС =VА/АС и (VВ – VА)/АВ= 1 – 2.
VВ
а /
с/
А
С
1
1
V
(S) А
А
С
Подставляя в последнее выражение VА и VВ, получим
= 1 – 2 и
/ АВ = 1 /ВС = 2 /АС .
(*)
Вывод. При сложении вращений, направленных в разные
стороны, результирующее движение будет мгновенным
вращением с абсолютной угловой скоростью = 1 – 2
вокруг мгновенной оси Сс /, параллельной данным осям,
положение которой определяется пропорциями (*).

6.

Случай 3. Пара вращений
Рассмотрим случай, когда вращения
В
направлены в разные стороны , но
по модулю 1= 2. Такая
2
совокупность вращений называется 2 В
парой вращений, а векторы 1 и 2
V
В
образуют пару угловых скоростей.
1
А
V
1
(S)
А
VА
Для скоростей точек А и В: VА = 2 · АВ, VВ = 1 ·АВ, т. е. VА = VВ.
М.ц.с. находится в бесконечности, поэтому скорости всех его
точек равны и численно определяться по формуле: V = 1 · АВ.
Вывод. В случае пары вращения движение тела будет
поступательным со скоростью численно равной 1 · АВ и
направленной
плоскости,
проходящей через
перпендикулярно
векторы 1 и 2 ;направление вектора V определяется так
же, как в статике определяется направление момента пары m.

7.

1 1
D
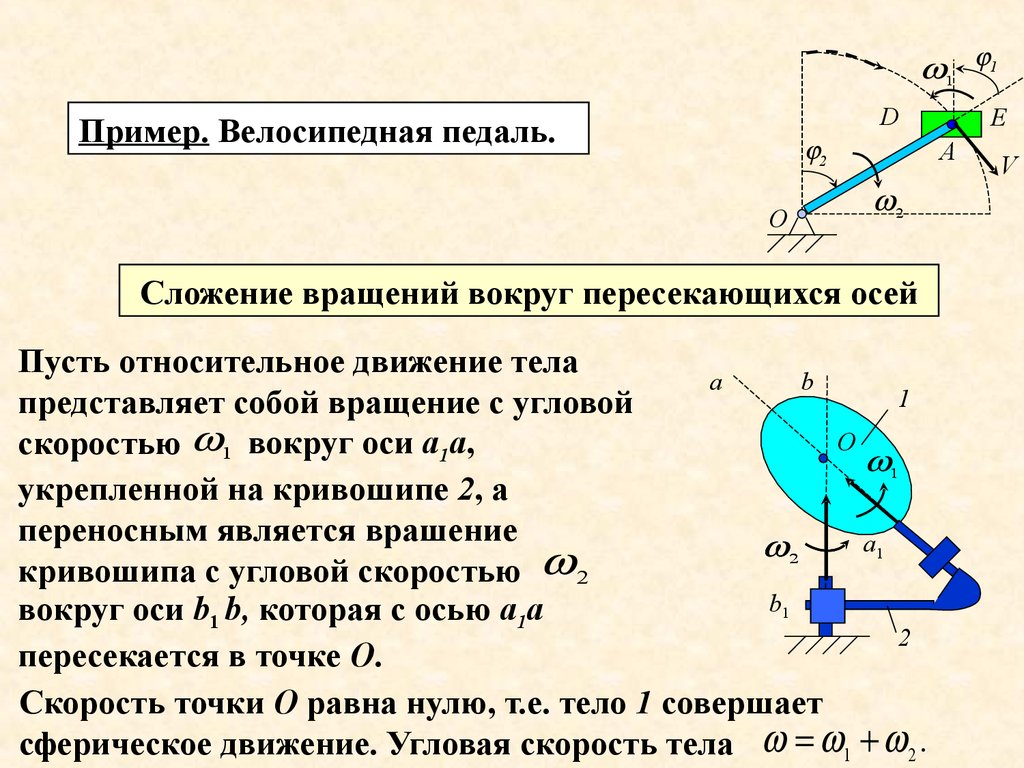
Пример. Велосипедная педаль.
2
О
Е
А
2
Сложение вращений вокруг пересекающихся осей
Пусть относительное движение тела
а
b
1
представляет
собой
вращение
с
угловой
О
скоростью 1 вокруг оси а1а,
1
укрепленной на кривошипе 2, а
переносным является врашение
а1
2
кривошипа с угловой скоростью
2
b1
вокруг оси b1 b, которая с осью а1а
2
пересекается в точке О.
Скорость точки О равна нулю, т.е. тело 1 совершает
сферическое движение. Угловая скорость тела 1 2 .
V

8.

Вывод. При сложении вокруг двух осей,
пересекающихся
в
точке
О,
результирующее движение тела будет
мгновенным вращением вокруг оси Ос,
проходящей через точку О, и угловая
скорость этого вращения будет равна
геометрической сумме относительной и
переносной угловых скоростей.
с
b
а
2
1
О
Мгновенная ось Ос направлена вдоль вектора , т. е. по
диагонали параллелограмма,
на векторах
построенного
1 и 2 .
Сложение вращений вокруг пересекающихся осей
Переносное движение – движение платформы со скоростью V .
Относительное движение – вращение с угловой скоростью .

9.

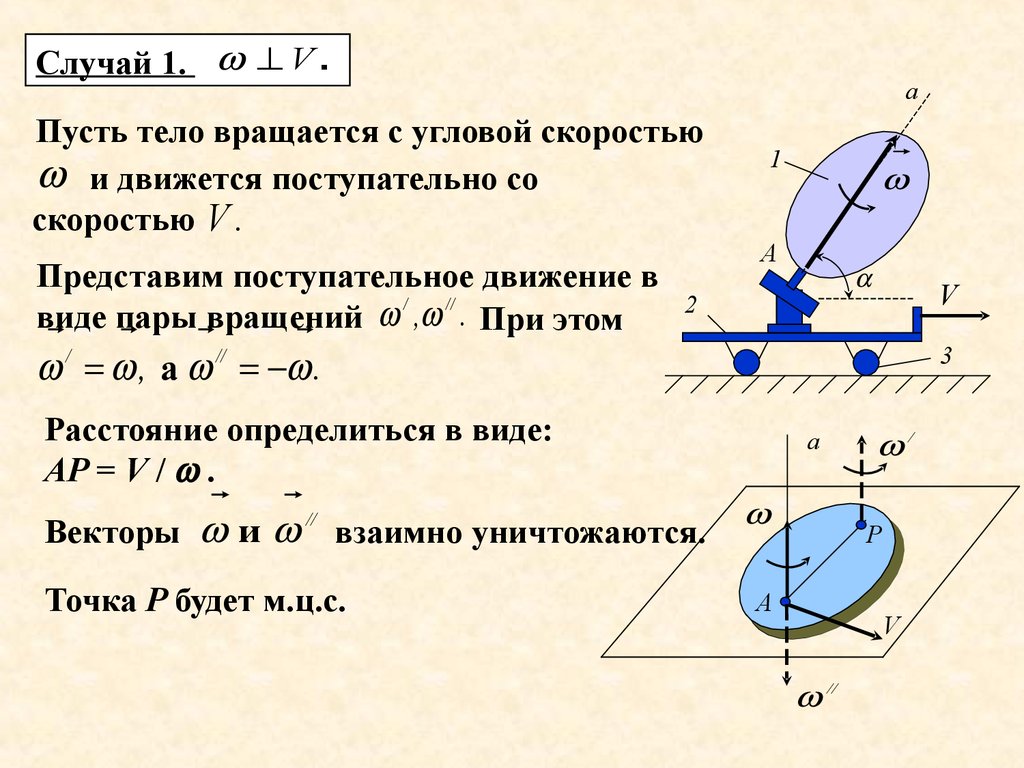
Случай 1. V .
а
Пусть тело вращается с угловой скоростью
и движется
поступательно со
скоростью V .
Представим поступательное
/ // движение в
виде пары вращений , . При этом
1
А
V
2
/
//
, а .
Расстояние определиться в виде:
АР = V / .
//
Векторы и взаимно уничтожаются.
Точка Р будет м.ц.с.
3
а
/
Р
V
А
//

10.

Случай 2. Винтовое движение (V || ).
Если сложное движение тела
складывается из вращательного
вокруг
оси Аа, с угловой скоростью
и поступательного со скоростью V ,
направленного параллельно оси Аа, то
движение называется винтовым.
Ось Аа называется осью винта.
а
V
М
V
h
А
Расстояние, проходимое за время одного оборота любой
точкой тела, не лежащей на оси винта, называется шагом h
винта. Можно показать, то h = 2 V / .