Similar presentations:
Линейная алгебра
1.
Линейнаяалгебра
2. Структура курса
-линейная алгебра;-векторная алгебра;
-аналитическая геометрия.
3. Литература
Математика. Ч. 1, 1 семестр: УМК /сост.:А.Б.Гончарова и др.– СПб.: CЗТУ, 2009.
Лобунина, И.И., Сентяков В.А. Математика, ч.1.
Линейная алгебра: УМК, учеб. пособие/ - СПб.:
СЗТУ, 2008
Романова, Ю.С., Математика, ч.1.
Аналитическая геометрия: УМК, учеб. пособие /
- СПб.: СЗТУ, 2008
4. Матрицы
ЛЕКЦИЯ 1Матрицы
5.
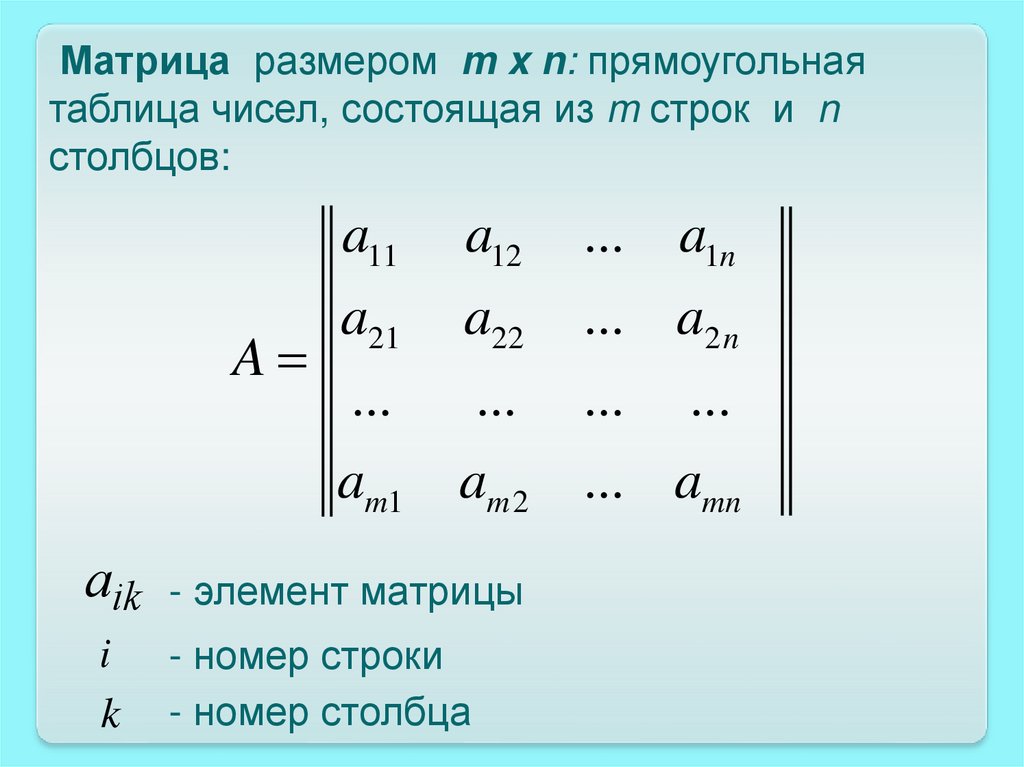
Матрица размером m x n: прямоугольнаятаблица чисел, состоящая из m строк и n
столбцов:
A
a11
a12
...
a21
a22
... a2 n
...
...
...
am1
aik
i
k
a1n
...
am 2 ... amn
- элемент матрицы
- номер строки
- номер столбца
6.
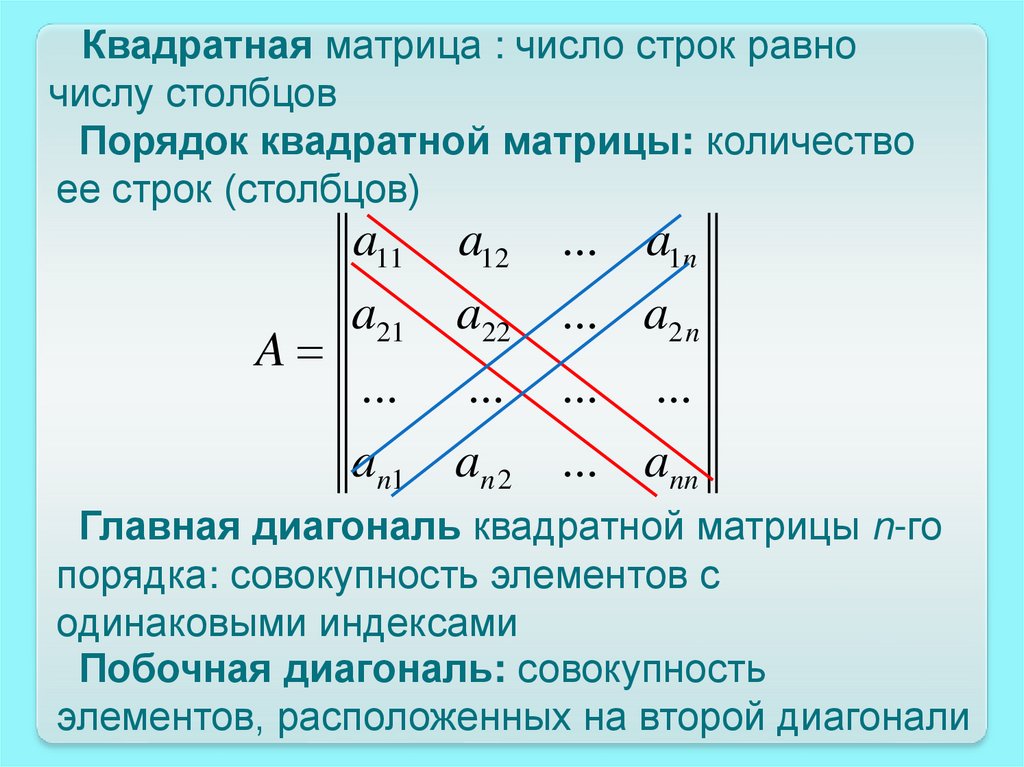
Квадратная матрица : число строк равночислу столбцов
Порядок квадратной матрицы: количество
ее строк (столбцов)
A
a11
a12
... a1n
a21
a22
... a2 n
...
...
...
an1
an 2
... ann
...
Главная диагональ квадратной матрицы n-го
порядка: совокупность элементов с
одинаковыми индексами
Побочная диагональ: совокупность
элементов, расположенных на второй диагонали
7.
Диагональная матрица:квадратная матрица, все
элементы которой,
расположенные вне
главной диагонали,
равны нулю
Единичная матрица:
диагональная матрица
n-го порядка, все
диагональные элементы
которой равны единице
a11
0
0
D 0
a22
0
0
0
a33
1 0 0
E 0 1 0
0 0 1
8.
Операции над матрицамиРавные матрицы A и B: имеют одинаковый
размер и их соответствующие элементы равны :
aik bik (i 1,2,..., m;
k 1,2,..., n).
Произведение матрицы A на число
B A A .
:
Сумма матриц A и B, имеющих одинаковый
размер: матрица C, каждый элемент которой
равен сумме соответствующих элементов
матриц A и B:
cik aik bik
9.
Разность матриц A и B, имеющих одинаковыйразмер: матрица D, каждый элемент которой
равен сумме соответствующих элементов
матриц A и (-1)хB:
dik aik ( 1) bik
Транспонированная матрица: столбцы
матрицы А являются строками матрицы AT
A
3 2 4
1
0
2
3
1
AТ 2 0
4
2
10.
Пример.3 2 4
1
0
2
3
1 3 2
0 1 5
3 3 1 2 3 ( 3) 4 3 2
1 3 0
0 3 ( 1)
6
7
10
1 3 17
2 3 5
11.
Произведение матрицы A (m x p) на матрицуB(p x n) : матрица C (m x n), каждый элемент
которой равен
cik ai1b1k ai 2b2 k aimbmk
Свойства операции умножения матриц
1. Перемножение матриц некоммутативно:
A B -произведение матрицы A на матрицу
B справа
B A -произведение матрицы A на матрицу
B слева
Перестановочные матрицы:
2. AEn En A A
A B B A
12.
Пример. Вычислить произведение матрицы Ана матрицу В справа:
A
2
1
3 0
3 1 1
,
2
B 0
3
2
1
13.
A B2
3 0
3 1 1
1
0
2
2
3
1
( 2) ( 1) 3 0 0 2
( 2) 2 3 ( 3) 0 1
3 ( 1) ( 1) 0 1 2
3 2 ( 1) ( 3) 1 1
2
13
1
10
14.
Пример. Вычислить произведение матрицы Ана матрицу В слева.
1
2
0
3
2
1
B A
2
3 0
3 1 1
( 1) ( 2) 2 3
( 1) 3 2 ( 1)
( 1) 0 2 1
0 ( 2) ( 3) 3
0 3 ( 3) ( 1)
0 0 ( 3) 1
2 ( 2) 1 3
2 3 1 ( 1)
8
5
2
9
3
3
1
5
1
2 0 1 1
15.
Пример. Доказать, что матрицы А и Вперестановочные
A
A B
3 5
1 2
3 5
B
1 2
1
5
1
2
1
5
1
2
3 5 15 10
1 2
5 4
2 5
1 1
2 5
5 3 5
3 5 5 10
B A
1 1
1 2 1 2
3 2 5 4
1
16.
Определители квадратных матрицОпределитель матрицы второго порядка:
A
a11
a12
a21
a22
число, равное разности произведений элементов
главной и побочной диагоналей матрицы
a11
a12
a21
a22
a11a22 a12 a21
17.
Пример. Вычислить определитель матрицыA
8 2
3
1
8 2
3
1
8 1 3 ( 2) 8 6 14
18.
a11a12
a13
A a21 a22
a23
a31
a33
a32
Минор M ik элемента aik матрицы третьего
порядка: определитель матрицы второго
порядка, получающейся из данной матрицы
вычеркиванием i-ой строки и k-гo столбца, на
пересечении которых находится этот элемент.
M 12
a21
a23
a31
a33
19.
Алгебраическое дополнение элемента aikматрицы третьего порядка: число, равное
i k
(
1
)
произведению минора этого элемента на
.
Aik ( 1)
i k
2 1
Пример.
A
A21 ( 1)
1 0
0 1
1;
0
1 3 1
2
2 1
M ik
0
1
A33 ( 1)
3 3 2
1
1 3
5.
20.
Определитель матрицы третьего порядка:число, равное сумме произведений элементов
любой строки (столбца) матрицы на их
алгебраические дополнения
a11
a12
a13
a21
a22
a23 a11 A11 a12 A12 a13 A13
a31
a32
a33
- разложение определителя по строке
21.
Пример. Вычислить определитель матрицыразложением по первой строке
2 1
1
A 1
2 3
1
1 1
2 1
1
1
2
3 2 A11 ( 1) A12 1A 13 2( 1)
1
1
1
1 1
1 2
( 1)( 1)
2 3
1 1
1 3
1 3 1 2
1( 1)
1 1
1 1
2 1 1 2 1( 1) 3.
22.
Пример. Вычислить определитель матрицыразложением по второму столбцу
2 1
A 1
2 3
1
1 1
2 1
1
1
2
3 ( 1) A12 2 A22 1 A 32
1
1
1
1 2
( 1)( 1)
1 3
1 1
2( 1)
2 2
2
1
1
1 1
1( 1)
3 2
1 2 2 ( 3) ( 1) ( 7) 3.
2
1
1 3
23.
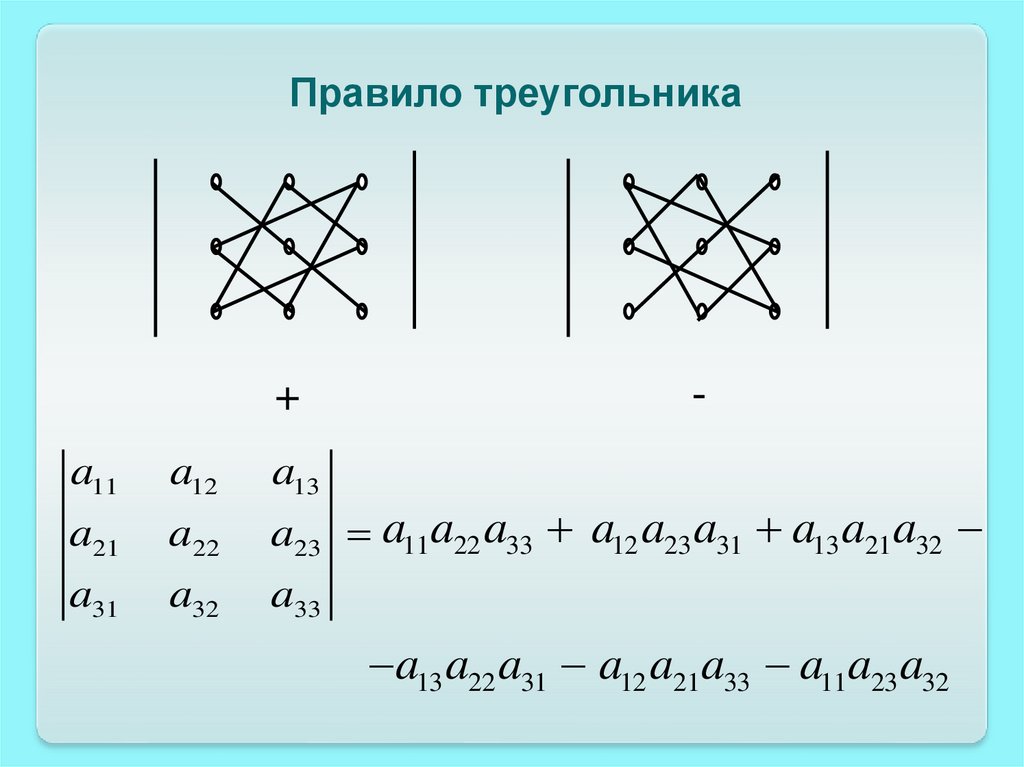
Правило треугольника+
-
a11
a12
a13
a21
a22
a23 a11 a22 a33 a12 a23 a31 a13 a21 a32
a31
a32
a33
a13 a22 a31 a12 a21a33 a11a23 a32
24.
Пример. Вычислить определитель матрицы поправилу треугольника
2 1 1
2 1
1
1
2
3
1
1
1
A 1
2 3
1
1 1
2 2( 1) ( 1)( 3)1 1 1 1
1 2 1 ( 1)1( 1) 2( 3) 1
4 3 1 2 1 6 3
25.
Пример . Вычислить определитель, разложивего по элементам первого столбца
3
2
4
2 1 3 1
3 1
0
1
1 1
4 1
2 1
2 1
3 1
2 1
3
0 1
1
3 1
2
1
2 1
3 1 1 4 1 1 0 3 4 1
26.
Пример . Вычислить определитель, используяправило треугольника
3
2
4
2 1
0
3
1
1
3 ( 2) 1 2 1 0 4 3 1
1 ( 2) 0 2 4 1 ( 1) 3 ( 3)
6 0 12 0 8 9 1
27.
Основные свойства определителей1.Определитель транспонированной матрицы
равен определителю исходной матрицы
D( AТ ) D( A)
2. Сумма произведений элементов какой-либо
строки (столбца) матрицы на алгебраические
дополнения элементов другой строки (столбца)
равна нулю.
3. При перестановке двух строк (столбцов)
местами определитель меняет знак.
4. Определитель с одинаковыми
(столбцами) равен нулю.
строками
28.
5. Умножение определителя на числоэквивалентно умножению строки (столбца) на
это же число.
6. Определитель с нулевой строкой (столбцом)
равен нулю.
7. Определитель матрицы не изменится, если к
элементам
какой-либо
строки
(столбца)
прибавить соответствующие элементы другой
строки (столбца), умноженные на одно и то же
число.
8. Определитель произведения квадратных
матриц равен произведению определителей
этих матриц:
A B A B
29.
Пример. Вычислить определительD
1
2
1
4
0
5
6
8
2
9
8
16
1
4
10 8
*2+
1
2
1
4
2
9
8
16
2
9
8
16
1
4
10 8
0
30.
Пример.2 1
D 4
2
2 1
0
*2+
3 2
6
0
3
1
1
5 8
0
6
*(-5)+
0
0
2( 28) 56
*(-3)+
1 4
2
2 1
3
4
2 1 3
1
1
3
4
0 28
31.
Обратная матрицаКвадратная матрица А называется обратимой,
если существует обратная к ней матрица A 1 ,
удовлетворяющая соотношениям
A A A A E
1
1
Теорема. Для того, чтобы матрица А имела
обратную матрицу, необходимо и достаточно,
чтобы определитель ее был не равен нулю;
тогда матрица А –невырожденная и
A11
1
A
A12
D ( A)
A13
1
A21
A31
A22
A32
A23
A33
32.
Свойства обратных матриц1 1
1. A
A
A
T 1
1 T
2. A
3. A B B 1 A 1
1
1
4. D( A )
D( A)
1
33.
Пример. Найти обратную матрицу для матрицы1 2
A
1
1 2
2
1 0
1 2
1
1
0
1
0
D ( A) 2 1 2 2 3 4 1( 1)
1 0 1 1 2 2
1 1
3 4
2
2
2
34.
1 1A11 ( 1)
0
A12 ( 1)1 2
1 3
A13 ( 1)
1
2 1
2 2
1 0 1
2
2
1
1
2
1
1 0
A21 ( 1)
A22 ( 1)
1 2
2 1
0 1
1 1
1 1
(2 2) 0
0 1 1
(2 0) 2
1 1 2
1 2
1
2 1 2
1 0
1
35.
A23 ( 1)A31 ( 1)
A32 ( 1)
1 2
2 3
1 0
3 1
3 2
A33 ( 1)3 3
2
1
1 2
1
1
(0 2) 2
1 0
( 2 2) 4
2 2
1 2
1 4 3
2 1
1
A 0
2 4
2
1 2 3
1
2 1 2
4 1 5
1 2 5
1
1 2
0,5 1 2,5
0
1
2
0,5 1 1,5
1
36.
Проверка:1 0,5 1 2,5
1 2
1
A A 2 1 2
1 0
1
2
1 0,5 1 1,5
0,5 0 0,5
0
1 2 1 2,5 4 1,5
1 0 1 2 1 2
0,5 0 0,5
1 0 1
1 0 0
0 1 0 E
0 0 1
5 2 3
2,5 0 1,5
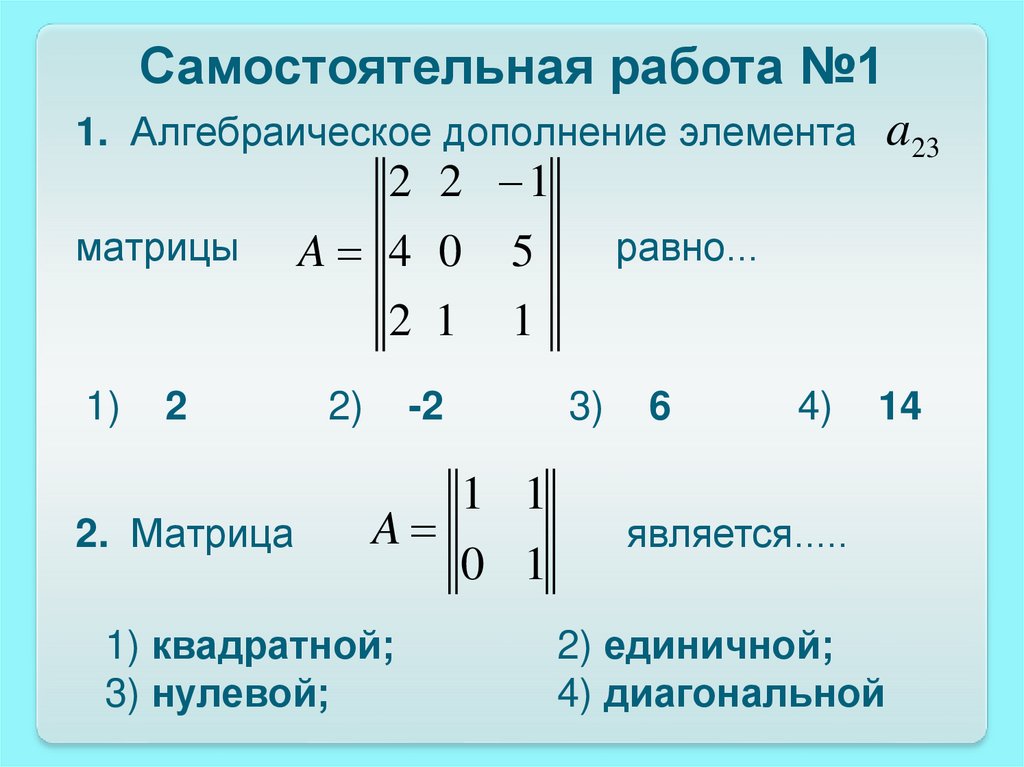
37. Самостоятельная работа №1
1. Алгебраическое дополнение элементаa23
2 2 1
матрицы
1)
2
2. Матрица
A 4 0
5
2 1
1
2)
-2
A
1) квадратной;
3) нулевой;
равно...
3)
1 1
0 1
6
4)
14
является.....
2) единичной;
4) диагональной
38. Самостоятельная работа №1
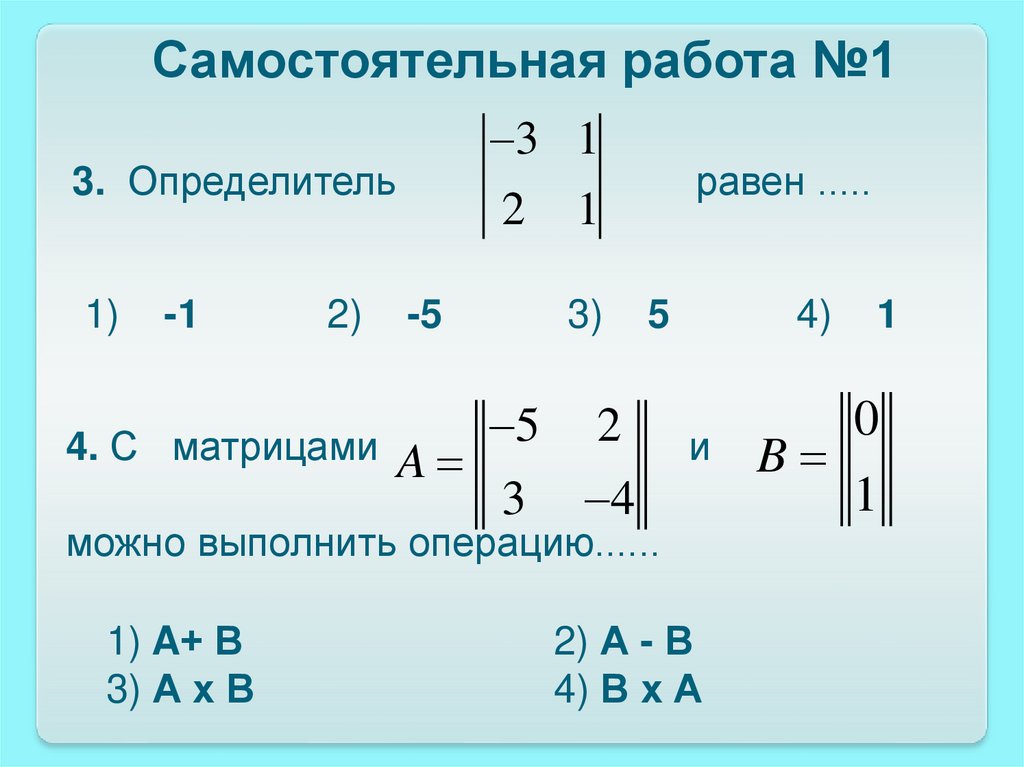
3 13. Определитель
1)
-1
2)
4. С матрицами
2
-5
A
равен .....
1
3)
5
2
3
4
5
4)
и
можно выполнить операцию......
1) A+ В
3) А х В
2) А - В
4) В х А
B
1
0
1
39. Самостоятельная работа №1
5. Сумма элементов побочной диагоналиматрицы произведения матрицы
B
4
5 0
6 1 3
1
на матрицу
A 5 0
4
слева равно.....
1)
13
2)
-18
3)
3
30
4)
7
-30
40.
Самостоятельная работа №1a11 a12
1. Если определитель матрицы A
a21 a22
равен D, то определитель
матрицы B k A равен…..
2
kD
1)
2) k D
3) 2kD
4) D
a11 a12
2. Если определитель матрицы A
a21 a22
равен D, то определитель
обратной к ней матрицы равен…..
1) D
3) 2D
2
D
2)
4) 1/ D
41.
Самостоятельная работа №13. Матрица
1 k
1
3
является обратной
3 4
по отношению к матрице
1
1
1) 4
2) 2
3) -4
4) 0
при k=…
4. Если в определителе четвертого порядка
поменять местами второй и четвертый столбец,
то определитель…
1)изменит знак
3) обратится в нуль
2) не изменится
4) удвоится





































 mathematics
mathematics








