Линейная алгебра

1.

Линейная алгебра
Байков Андрей Юрьевич
Литература
1)
Дм. Письменный «Конспект лекций по высшей математике» /М.: Арис-Пресс
(стереотипное)
2)
Байков А.Ю. Линейная алгебра. Краткий конспект лекций для студентов
обучающихся по специальности Экономика/ М.: МФЮА, 2012
1

2.

1. Вектор-столбцы и вектор-строки
Вектор-столбец
a1
a2
a
...
an
Вектор-строка
a * a1
dim a n
a 2 ...
an
dim a * n
Транспонирование:
a
T
a
- размерность
*
a
* T
a
Схематические изображения
- столбец
строка
2

3.

2. Операции над столбцами и строками
Линейные операции (сложение и умножение на число)
dim a dim b n
+
=
a1
b1 a1 b1
a
b
a
b
2
a b 2 2 2
...
... ...
an
bn an bn
b1
b2
an
a1b1 a2b2 ... anbn
...
bn
Умножение строки на столбец
a * b a1
=
a2 ...
3

4.

a11 a12
a21 a22
A
...
...
an1 an 2
dim A n m
a1*
*
a2
A
...
*
an
...
...
...
...
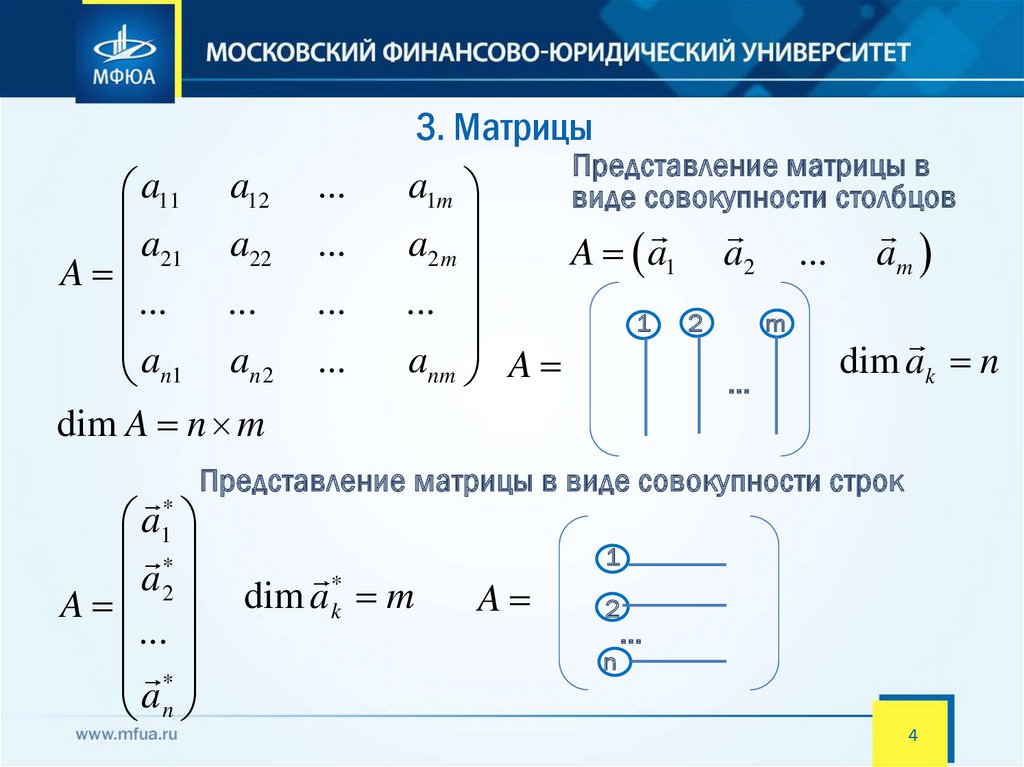
3. Матрицы
Представление матрицы в
a1m
виде совокупности столбцов
a2 m
A a1 a2 ... am
...
m
1 2
anm A
dim
a
n
k
…
Представление матрицы в виде совокупности строк
dim a *k m
1
A
2
n
…
4

5.

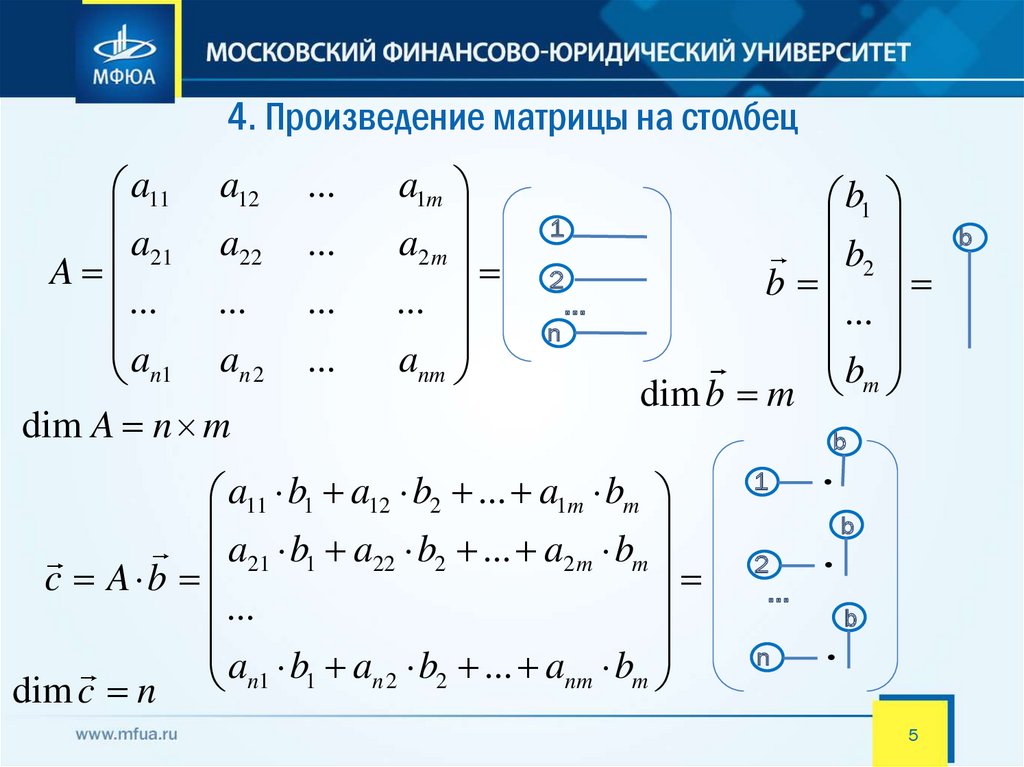
4. Произведение матрицы на столбец
a11 a12
a
a
21
22
A
...
...
an1 an 2
dim A n m
...
...
...
...
a1m
a2 m
...
anm
1
2
n
…
b1
b2
b
...
bm
dim b m
a11 b1 a12 b2 ... a1m bm
a
b
a
b
...
a
b
2m
m
c A b 21 1 22 2
...
an1 b1 an 2 b2 ... anm bm
dim c n
b
1
2
…
n
b
b
5
b

6.

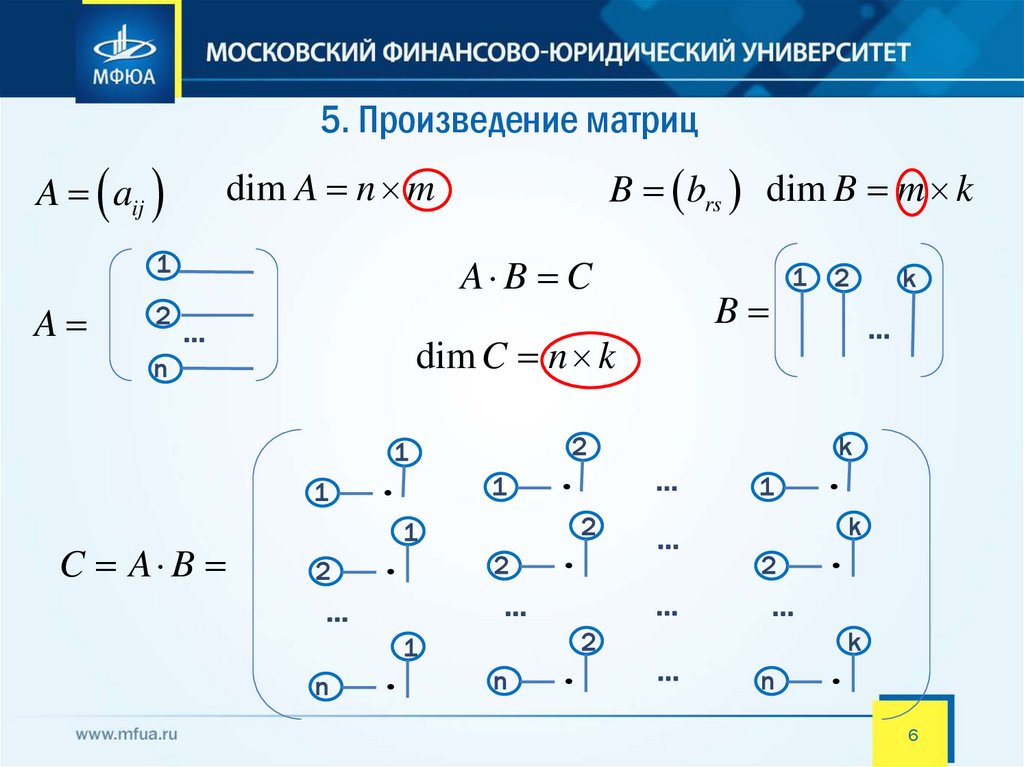
5. Произведение матриц
A aij
1
A
2
B brs dim B m k
dim A n m
A B C
…
1
2
…
n
1
1
2
…
1
n
…
…
2
k
k
…
2
2
…
2
1
C A B
B
dim C n k
n
1
…
1
2
…
n
k
k
6

7.

6. Пример произведения матриц
9 10
1 2 3 4
12 13
A
B
5 6 7 8
15 16
dim A 2 4
18 19
C A B
dim B 4 3
dim C 2 3
Пусть
С с1 с2
11
14
17
20
с3
1 9 2 12 3 15 4 18 150
с1
5
9
6
12
7
15
8
18
366
7

8.

6. Пример произведения матриц (продолжение)
1 10 2 13 3 16 4 19 160
с2
5
10
6
13
7
16
8
19
392
1 11 2 14 3 17 4 20 170
с3
5
11
6
14
7
17
8
20
418
150 160 170
С
366
392
418
8

9.

1-6. Задачи-1
В задачах 1-2 найти все возможные произведения матриц
1
1) A
0
0 1 2
2 0 1
C 1 2 3 4
1
0
D
2
5
1 0
E
0 1
1 3
0
2
B
1 0
3 1
1
F
1
9

10.

1-6. Задачи-2
В задачах 1-2 найти все возможные произведения матриц
2)
1 0 2
B 0 1 1
4 5 0
1 2 3
A 4 5 6
7 8 9
C 1 2 3
1
D 0
2
1 0
E
0
1
1
F
1
10

11.

7. Квадратные матрицы
A aij
Если
dim A n n
- квадратная матрица размерности
dim B n n , то A B C , B A D
dim C dim D n n
C D
aii - главная диагональ квадратной матрицы
Диагональные матрицы
0
0
a11
0
...
0
0
...
a22 ...
...
...
0
...
0
0
...
ann
diag a11 , a22 ,...ann
11
n

12.

8.Особые виды квадратных матриц
Нулевая матрица
0
0
O
...
0
Единичная матрица
... 0
0 ... 0
... ... ...
0 ... 0
1
0
E
...
0
0
A O O A A
Треугольная матрица
a11
0
T
...
0
a12
...
a22
...
...
...
0
...
a1n
a2 n
...
ann
... 0
1 ... 0
diag 1,1,...1
... ... ...
0 ... 1
0
A E E A A
Симметричная матрица
ST S
12

13.

9.Дополнительная матрица
a11
a21
...
A
am1
...
an1
a12
...
a1k
...
a22
...
a2 k
...
...
...
...
...
am 2 ...
amk
...
...
...
...
...
an 2
...
ank
...
a1n
a2 n
...
amn
...
ann
m
k
Матрица размерности (n-1)×(n-1), получающаяся
вычеркиванием m-й строки и k-го столбца из исходной матрицы,
называется дополнительной матрицей к элементу amk
13

14.

10. Определитель квадратной матрицы
det A A
a11
a12
...
a1n
a21
a21
...
a2 n
Определитель
дополнительной матрицы
an1 an 2 ... ann
называется минором.
Определитель дополнительной к элементу amk матрицы, взятый со
знаком «+», если сумма m+k четная и со знаком «-», если сумма m+k
нечетная, называется алгебраическим дополнением элемента amk
Будем обозначать его Amk
Определение по индукции
1) Если dim(A)=1×1, т.е. A=(a), то det(A)=a
...
2) Если dim(A)=n×n, то
или
...
...
...
det A am1 Am1 am 2 Am 2 ... amn Amn
det A a1k A1k a2 k A2 k ... ank Ank
14

15.

10. Определитель квадратной матрицы (продолжение)
Чередование знаков алгебраического дополнения
mij , i j 2 p
i j
Aij
1 mij
mij , i j 2 p 1
Определитель матрицы 2х2
...
...
...
... ... ... ...
a b
A11 d A12 c
a b
det A
A
c d
A21 b A22 a
c d
a A11 b A12 c A21 d A22 a A11 c A21 d A12 d A22
a d b c
15

16.

11. Определитель 3x3
a11 a12 a13
a22 a23
A
a
a
a
a
11
22
33
23
32
A a21 a22 a23
a32 a33
a a a
31 32 33
a21 a23
a21 a22
A12
a21 a33 a23 a31 A13
a21 a32 a22 a31
a31 a33
a31 a32
a11 a12 a13
det A a21 a22 a23 a11 A11 a12 A12 a13 A13
a31 a32 a33
16

17.

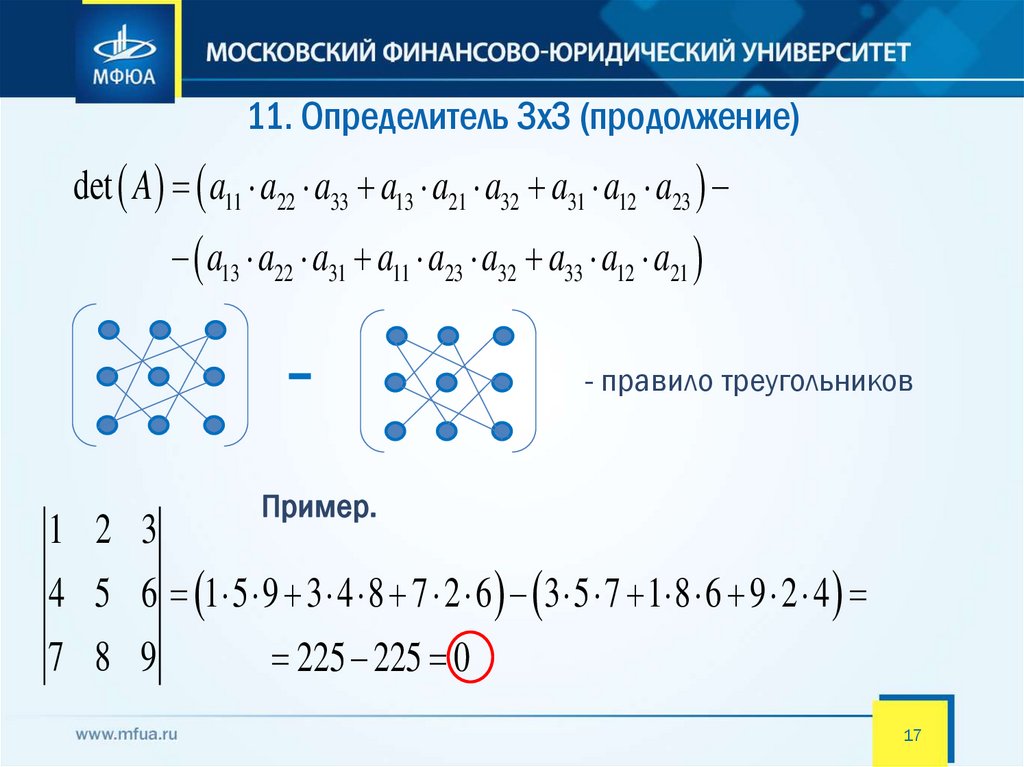
11. Определитель 3x3 (продолжение)
det A a11 a22 a33 a13 a21 a32 a31 a12 a23
a13 a22 a31 a11 a23 a32 a33 a12 a21
- правило треугольников
1 2 3
Пример.
4 5 6 1 5 9 3 4 8 7 2 6 3 5 7 1 8 6 9 2 4
7 8 9
225 225 0
17

18.

12. Свойства определителя
1) det AT det A
2) det A B det A det B
3) Если какая-либо строка (столбец) определителя
состоит из одних нулей, то определитель равен 0.
4) Если все элементы любой строки (столбца) умножить на
число α, то и определитель умножится на это же число α.
5) Если определитель содержит две одинаковые строки
(два одинаковых столбца), то он равен нулю
6) При перестановке двух строк (столбцов) определителя он
меняет знак на противоположный.
7) Определитель не изменится, если к элементам какойлибо строки (столбца) прибавить соответствующие
элементы другой строки (столбца), предварительно
умноженные на одно и то же число.
18

19.

13. Эквивалентные преобразования матриц.
Эквивалентными называются преобразования матрицы, не
меняющие значение определителя, т.е. преобразования на
основе свойства 7.
Эквивалентные преобразования делаются с целью
получения строк (столбцов) с максимальным числом нулей.
Пример. Вычислить определитель.
1 2 4 8
1 2 4 7
0 0 0 1
1 2 4 7
a a a2
5 6 8 1
5 6 8 1
3 0 5 4
*
1
*
1
*
3 0 5 4
19

20.

13. Эквивалентные преобразования матриц (продолжение).
1 2 4
1 2 4
*
*
*
0 * 0 * 0 * 1 5 6 8 a2 a2 3a1 2 0 4
3 0 5
3 0 5
2
2 4
3 5
0 * 0 * 2 2 5 4 3 4
20

21.

7-13. Задачи-1.
1 2 4
1) 1 3 3
6
2) 5 3 8
5 4 1
1 0 0
4) 0 1 0
0 0 1
8 6
4
4 3
1 234 631
5) 0
1
0
0
764
1
4 2 3
3) 3 0
3
6
2
7
23 25 32
6) 46 50
23 25
65
7
21

22.

7-13. Задачи-2.
5 2 7 2
7)
9)
2 4
2 4
2 8
4 8
9 1
8
1 4 2 2
8)
0
2 4
4 4
2 3
4 8
6 1 10 0
1 21 76 256
1 4 2 2
267 41
7 14 21 28
0
2
0
0
2
84
0
0
0
1
10)
2 3
4 8
6 12 18 24
22

23.

7-13. Задачи-3.
11) Решить уравнение
12) Решить уравнение
1 x
2
2
1 x
1 x
2
x
1 x
0
0
13) det diag a1 , a2 ,...an
23

24.

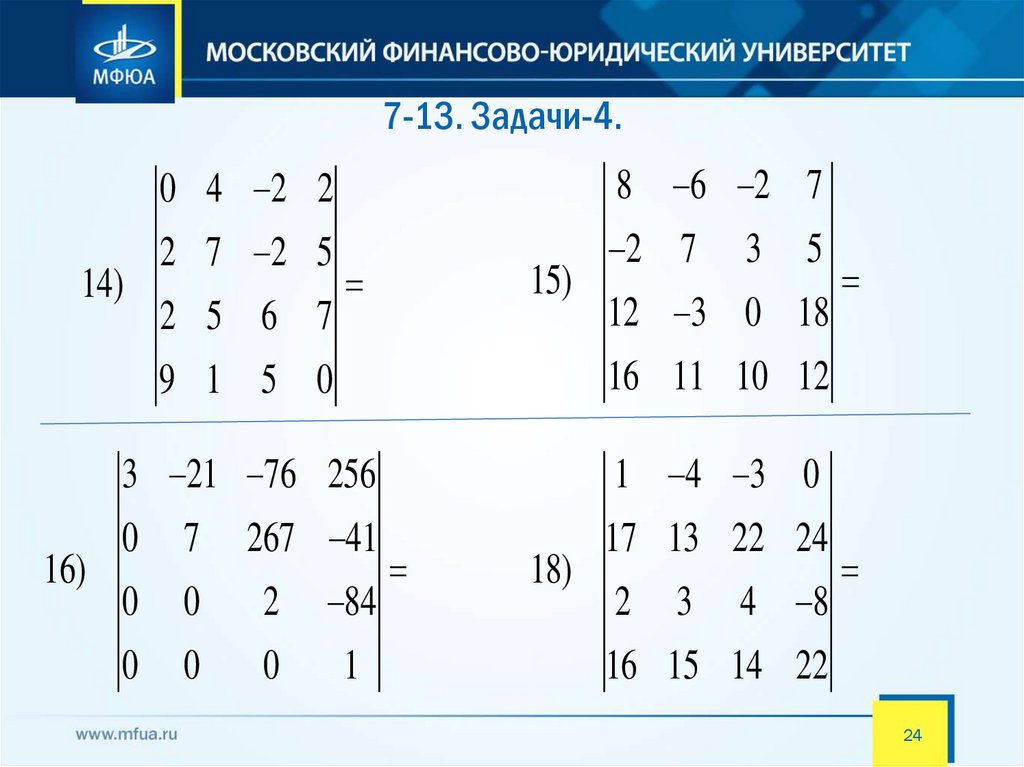
7-13. Задачи-4.
14)
16)
0 4 2 2
8 6 2 7
2 7 2 5
2 7
2 5 6 7
15)
3
5
12 3 0 18
9 1 5 0
16 11 10 12
3 21 76 256
1 4 3 0
267 41
17 13 22 24
0
7
0
0
2
84
0
0
0
1
18)
2
3
4 8
16 15 14 22
24