Similar presentations:
Линейная алгебра. Введение. Матрицы (лекция 1)
1.
МАТЕМАТИКАЛекция 1
2.
Лекцию читаетк.т.н., профессор
БОБРОВА Людмила
Владимировна
lvbobr@mail.ru
3.
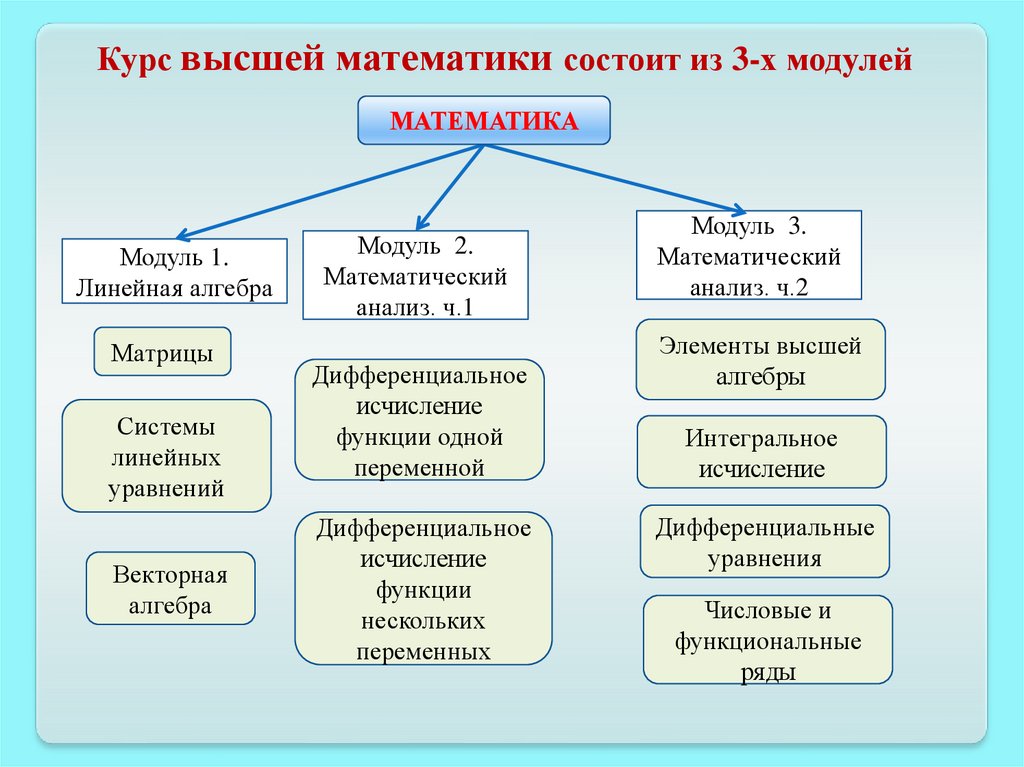
Курс высшей математики состоит из 3-х модулейМАТЕМАТИКА
Модуль 1.
Линейная алгебра
Матрицы
Системы
линейных
уравнений
Векторная
алгебра
Модуль 2.
Математический
анализ. ч.1
Дифференциальное
исчисление
функции одной
переменной
Дифференциальное
исчисление
функции
нескольких
переменных
Модуль 3.
Математический
анализ. ч.2
Элементы высшей
алгебры
Интегральное
исчисление
Дифференциальные
уравнения
Числовые и
функциональные
ряды
4.
Студенты всех направлений обученияпри работе с дисциплинами математического цикла
изучают теоретический материал, выполняют контрольные
задания, отвечают на вопросы тестов
на сайте дистанционного обучения института
5.
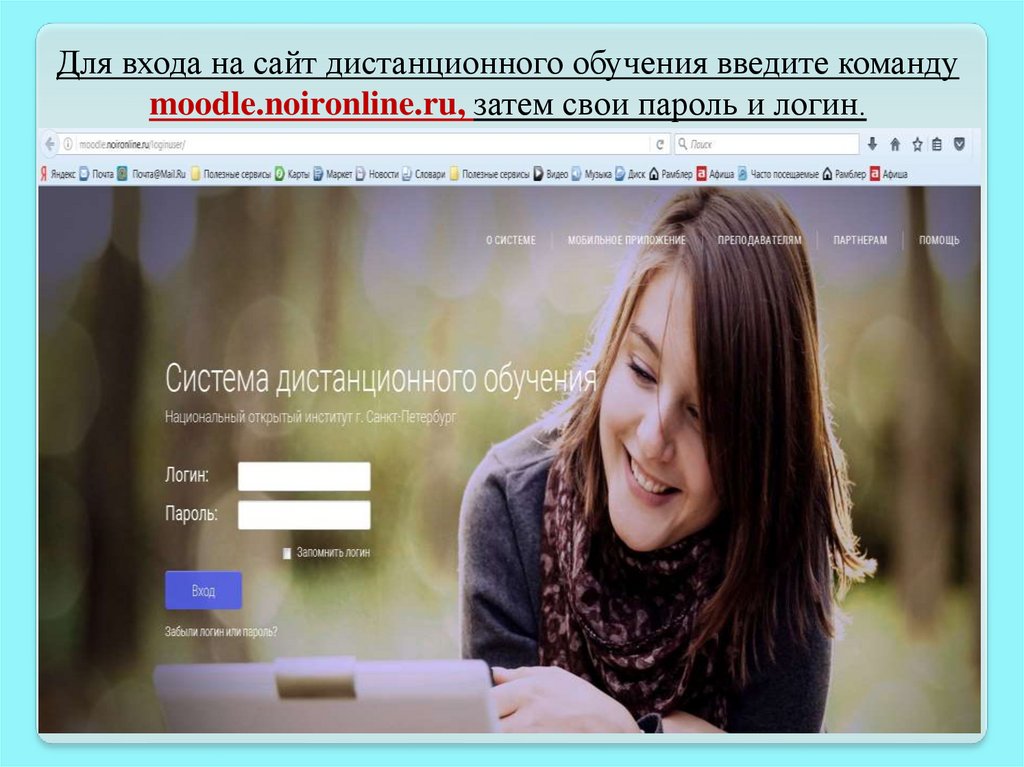
Для входа на сайт дистанционного обучения введите командуmoodle.noironline.ru, затем свои пароль и логин.
6.
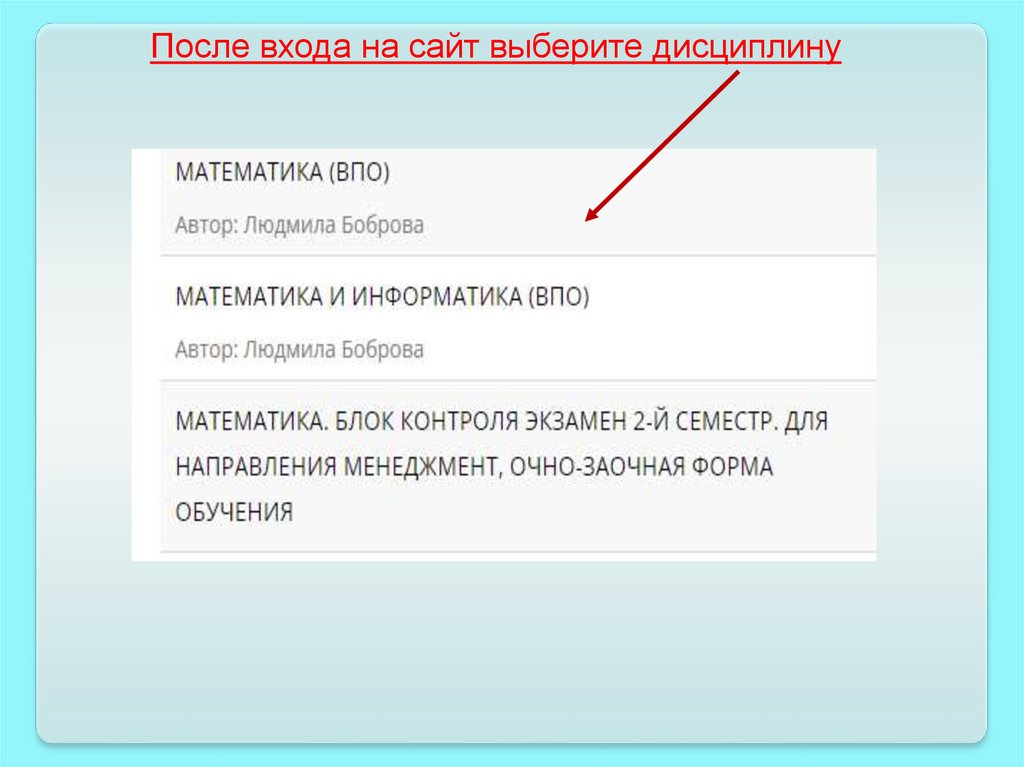
После входа на сайт выберите дисциплину7.
Структура любой дисциплины на сайте дистанционного обучения:Теоретический
материал
Информационный
блок
Блок контроля
8.
Теоретическая часть состоит из модулей (разделов):9.
При щелчкепо имени
раздела
раскрывается его
содержимое
(перечень тем)
10.
При щелчке по имени темы раскрывается ее содержимое:11.
Структура любого раздела:- теория по каждой теме;
- тренировочные тесты по
темам;
- вопросы для самопроверки
по модулю.
12.
РЕКОМЕНДУЕМЫЙ АЛГОРИТМ РАБОТЫ:1. Определить, какие виды работ и заданий предстоит
выполнить по данной дисциплине.
Оценка по дисциплине выставляется автоматически,
программой, в зависимости от набранной суммы баллов, по
балльно-рейтинговой системе (БРС).
Для ознакомления с БРС по данной дисциплине нужно
открыть раздел «Как получить оценку» в верхней части
сайта дисциплины:
13.
14.
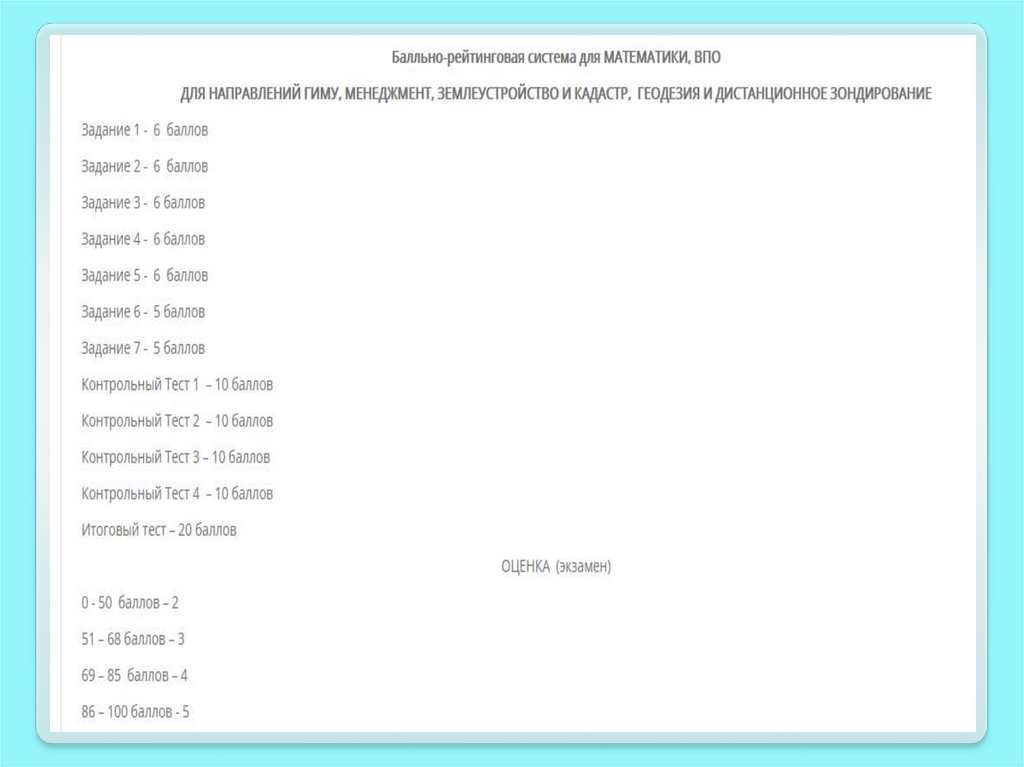
Балльно-рейтинговая система для студентов-психологов15.
РЕКОМЕНДУЕМЫЙ АЛГОРИТМ РАБОТЫ:Изучить теоретический материал раздела (по
материалу теоретического блока сайта дисциплины и
материалам лекции).
3. Перейти в контрольный блок для выполнения
практических заданий (по математике – решение задач
контрольной работы).
2.
16.
Блок контроля освоения дисциплинырасполагается ниже материала модулей
В Блоке контроля следует решить очередное задание
контрольной работы.
17.
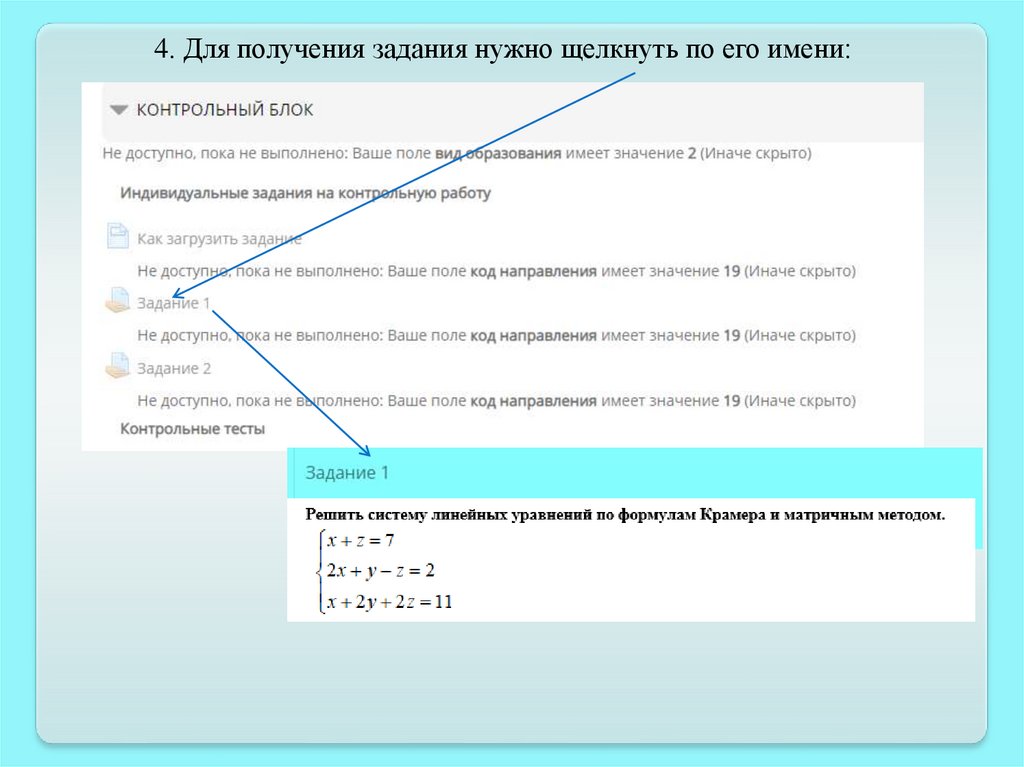
4. Для получения задания нужно щелкнуть по его имени:18.
5. По математике каждое задание выполняется:- либо на отдельном листе бумаги («вручную»), фотографируется и
сохраняется в одном из графических форматов (jpeg, pdf);
- либо в Worde.
6. Далее результат выполнения здания загружается на сайт
дисциплины согласно приведенным указаниям.
19.
Задания проверяются не автоматически,а преподавателем!
Срок проверки задания – в пределах недели.
Если допущены ошибки,
преподаватель напишет об этом в комментариях
даст возможность повторной загрузки задания.
ВОЗМОЖНЫ ВСЕГО ДВЕ ПОПЫТКИ
ЗАГРУЗКИ ЗАДАНИЯ
(больше не позволит система).
Так что будьте внимательны и не торопитесь!
20.
7. После изучения материалов раздела (темы) и выполненияконтрольного задания, отвечаете на вопросы теста по данному
разделу.
При работе с контрольным тестом дается 2 попытки и время
ограничено, поэтому лучше сначала потренироваться с
тренировочным тестом (для него нет ограничения на время и
количество попыток).
21.
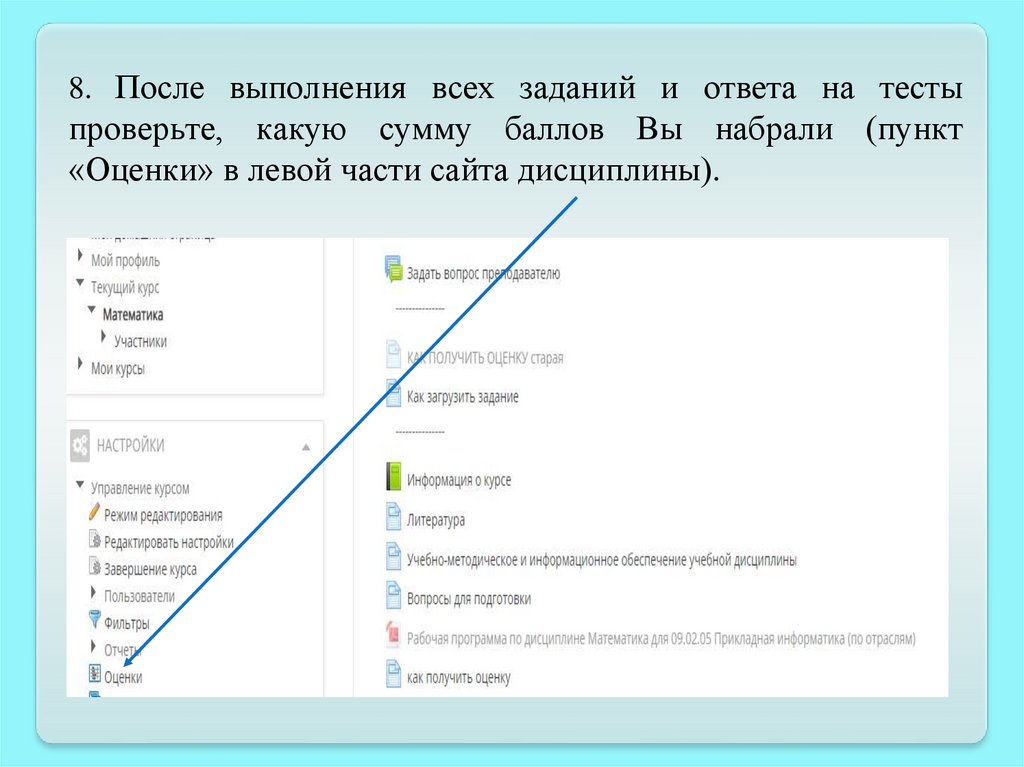
8. После выполнения всех заданий и ответа на тестыпроверьте, какую сумму баллов Вы набрали (пункт
«Оценки» в левой части сайта дисциплины).
22.
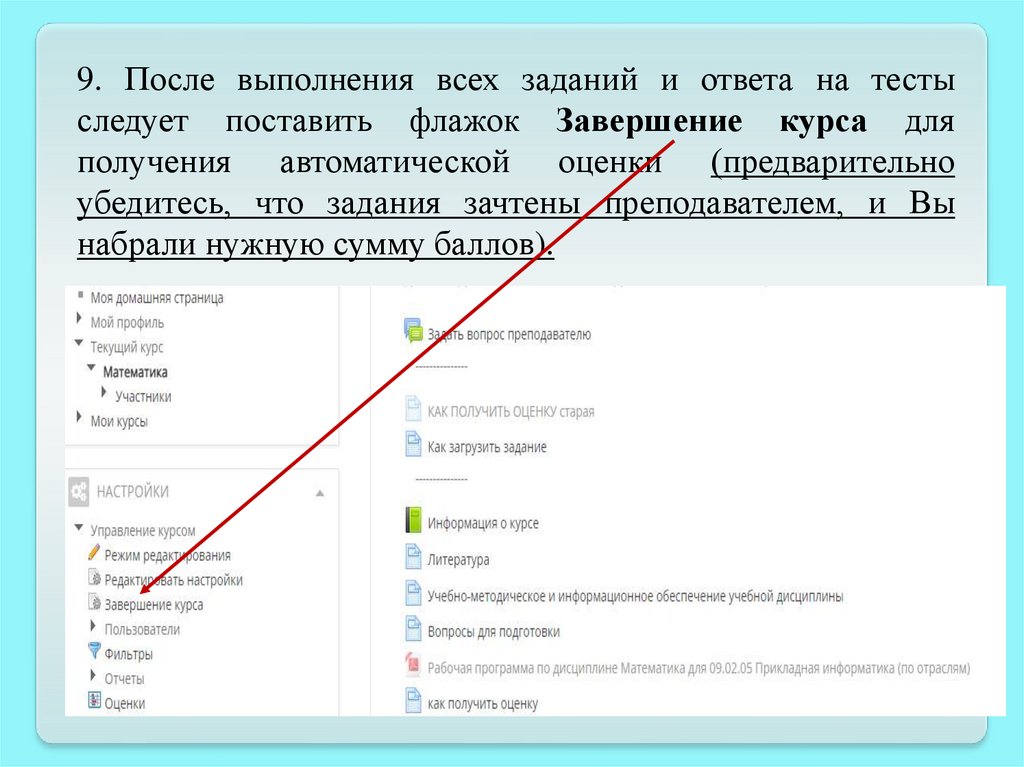
9. После выполнения всех заданий и ответа на тестыследует поставить флажок Завершение курса для
получения автоматической оценки (предварительно
убедитесь, что задания зачтены преподавателем, и Вы
набрали нужную сумму баллов).
23.
Студенты направленияГОСУДАРСТВЕННОЕ И МУНИЦИПАЛЬНОЕ
УПРАВЛЕНИЕ (ГиМУ)
изучают дисциплину МАТЕМАТИКА
только в первом семестре первого курса
(завершается экзаменом)
24.
Студенты направленияГОСУДАРСТВЕННОЕ И МУНИЦИПАЛЬНОЕ
УПРАВЛЕНИЕ (ГиМУ)
изучают дисциплину МАТЕМАТИКА
только в первом семестре первого курса
(завершается экзаменом)
Нужно зайти в
дисциплину
МАТЕМАТИКА (ВПО)
25.
При входе на сайт дисциплиныМАТЕМАТИКА (ВПО) студенты ГиМУ
получают доступ к 7 заданиям
контрольной работы
26.
27.
Студенты направленияМЕНЕДЖМЕНТ
изучают дисциплину МАТЕМАТИКА
в первом семестре первого курса
(завершается экзаменом)
и во втором семестре первого курса
(завершается экзаменом).
28.
Студенты направленияМЕНЕДЖМЕНТ
изучают дисциплину МАТЕМАТИКА
в первом семестре первого курса
(завершается экзаменом)
и во втором семестре первого курса
(завершается экзаменом).
В первом семестре
нужно зайти
в дисциплину
МАТЕМАТИКА (ВПО)
29.
При входе на сайт дисциплины МАТЕМАТИКА (ВПО)студенты-менеджеры получают доступ
к 6 заданиям контрольной работы
30.
31.
Студенты направленияМЕНЕДЖМЕНТ
изучают дисциплину МАТЕМАТИКА
в первом семестре первого курса
(завершается экзаменом)
и во втором семестре первого курса
(завершается экзаменом).
Во втором семестре
нужно зайти
в дисциплину
32.
При входе на сайт дисциплиныстуденты-менеджеры получают доступ
к 4-м заданиям контрольной работы
и 4-м тестам:
33.
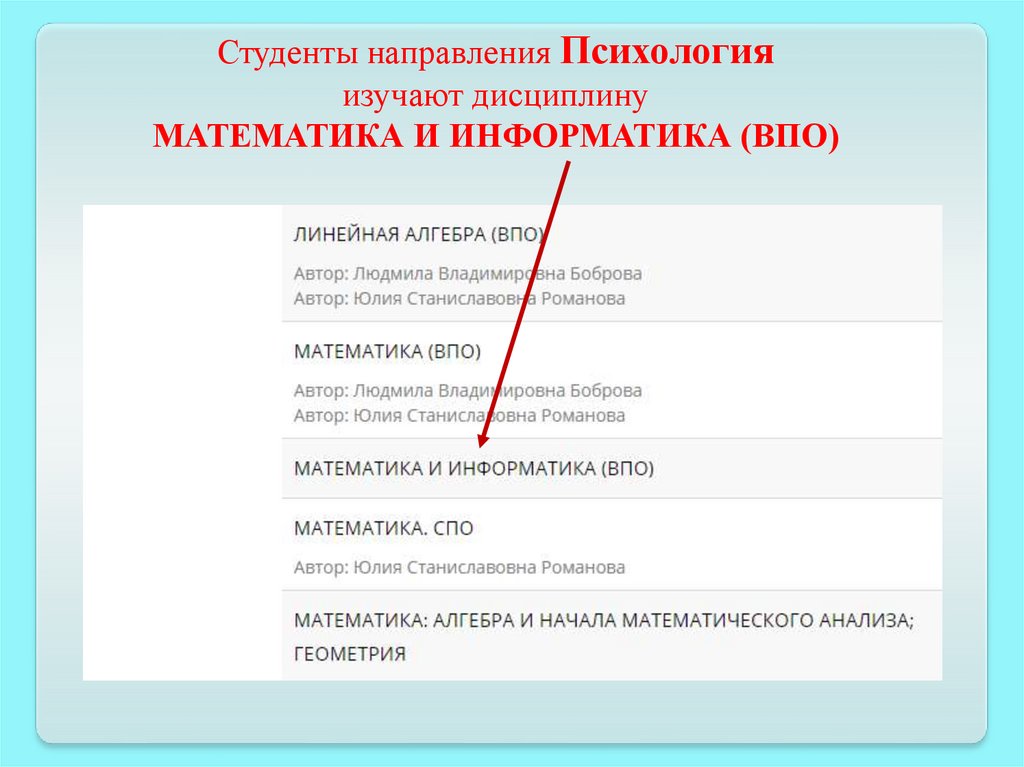
Студенты направления Психологияизучают дисциплину
МАТЕМАТИКА И ИНФОРМАТИКА (ВПО)
34.
При входе на сайт дисциплиныМАТЕМАТИКА И ИНФОРМАТИКА (ВПО)
студенты-психологи получают доступ
к 4-м заданиям контрольной работы,
2-м контрольным тестам и итоговому тесту
35.
СТРУКТУРА КУРСА-линейная алгебра;
-векторный анализ;
-аналитическая геометрия;
-математический анализ;
-дифференциальное исчисление функции одной
переменной
-интегральное исчисление функции одной
переменной
- теория вероятностей
36.
Модуль 1.ЛИНЕЙНАЯ АЛГЕБРА
37.
1.1.Матрицы38.
Матрица размером m x n:прямоугольная таблица чисел, состоящая
из m строк и n столбцов:
a11
a
21
A
...
am1
a12
a22
...
am 2
aik - элемент матрицы
i
k
- номер строки
- номер столбца
... a1n
... a2 n
... ...
... amn
39.
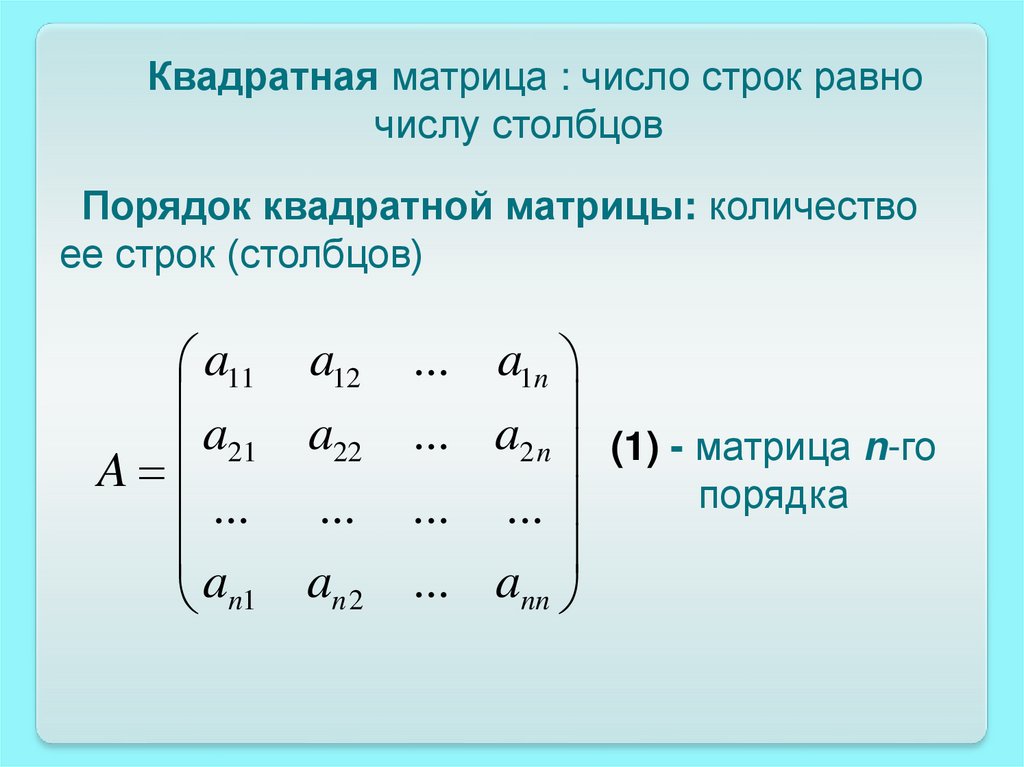
Квадратная матрица : число строк равночислу столбцов
Порядок квадратной матрицы: количество
ее строк (столбцов)
a11
a
21
A
...
an1
a12
a22
...
an 2
... a1n
... a2 n (1) - матрица n-го
порядка
... ...
... ann
40.
a11a
21
A
...
an1
a12
a22
...
an 2
... a1n
... a2 n
... ...
... ann
Главная диагональ квадратной матрицы:
совокупность элементов
с одинаковыми индексами
41.
a11a
21
A
...
an1
a12
a22
...
an 2
... a1n
... a2 n
... ...
... ann
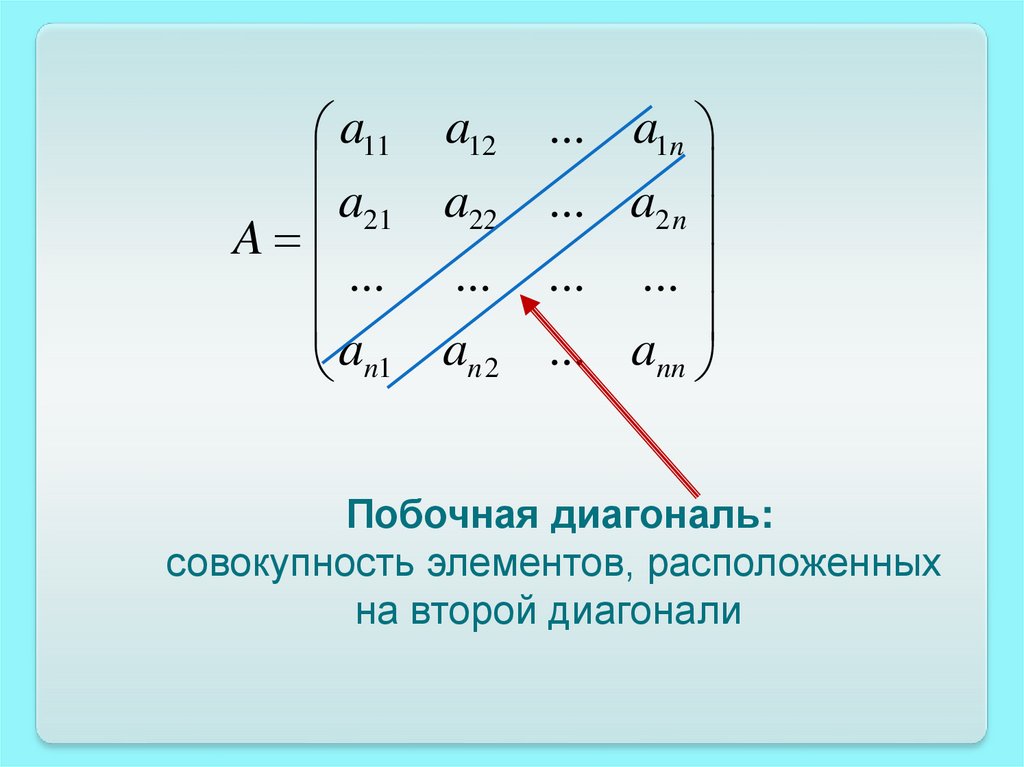
Побочная диагональ:
совокупность элементов, расположенных
на второй диагонали
42.
Диагональная матрица:квадратная матрица, все
элементы которой,
расположенные вне
главной диагонали,
равны нулю
a11
D 0
0
0
a22
0
0
0
a33
43.
Единичная матрица:диагональная матрица ,
все диагональные
элементы которой равны
единице
1 0 0
E 0 1 0
0 0 1
44.
1.2. Операциинад матрицами
45.
Равные матрицы A и B:имеют одинаковый размер и их
соответствующие элементы равны :
aik bik (i 1,2,..., m;
k 1,2,..., n).
46.
Равные матрицы A и B:имеют одинаковый размер и их
соответствующие элементы равны :
aik bik (i 1,2,..., m;
3 2 4
A
1 0 2
k 1,2,..., n).
3 2 4
ВA
1 0 2
47.
Произведение матрицы A на число :матрица B, такая что
B A A .
48.
Произведение матрицы A на число :матрица B, такая что
B A A .
Пример 1
5 2
4 1 2 5 ( 4) 5 1
5 0 7 3 5 0
5 7 5 ( 3)
6 0 8 5 6
5
0
5
8
20 5 10
0
35 15
30
0
40
49.
Сумма матриц A и B, имеющих одинаковыйразмер: матрица C, каждый элемент которой
равен сумме соответствующих элементов
матриц A и B:
cik aik bik
50.
Сумма матриц A и B, имеющих одинаковыйразмер: матрица C, каждый элемент которой
равен сумме соответствующих элементов
матриц A и B:
cik aik bik
Пример 2
2 1
А
4 6
7 3
В
0 5
51.
Пример 22 1
А
4 6
7 3
В
0 5
2 7 1 3 9 2
С А В
? 4 ?
4 0
52.
Самостоятельная работа 1Пример 2
2 1
А
4 6
7 3
В
0 5
2 7 1 3 9 2
С А В
? 4 ?
4 0
Чему равен элемент С22 ?
53.
Сверим ответы?cik aik bik
2 1
А
4 6
7 3
В
0 5
2 7 1 3 9 2
С А В
4 0 6 5 4 11
54.
Транспонирование матрицы:столбцы матрицы А являются
строками матрицы AT
Пример 3
3 2 4
A
1 0 2
3 1
Т
A 2 0
4 2
55.
Самостоятельная работа 2Задание. Какая из матриц является
транспонированной матрицей А?
2 1
А
4 6
A.
1 2
А
4 6
B.
C.
2 4
А
1 6
4 2
D. А 6 1
Т
Т
2 1
А
6 4
Т
Т
56.
1.3. Определителиматриц
57.
Определители матрицОпределитель матрицы второго порядка
a11
A
a21
a12
a22
это число, записанное в виде таблицы и равное
разности произведений элементов главной и
побочной диагоналей матрицы
a11
det A
a21
a12
a11a22 a12 a21
a22
58.
Пример 4. Вычислить определитель матрицы8 2
A
3 1
8 2
det A
8 1 3 ( 2) 8 6 14
3 1
59.
Самостоятельная работа 3Задание. Вычислить определитель матрицы
1 5
B
7 4
Варианты
A. 31
B. -31
ответов:
C. 27
D. 13
60.
Сверим ответы?1 5
det B
( 1) 4 7 ( 5) 4 35 31
7 4
1 5
B
7 4
61.
Миноры матрицМинор Mik элемента aik матрицы третьего
порядка: определитель матрицы второго
порядка, получающейся из данной матрицы
вычеркиванием i-ой строки и k-гo столбца, на
пересечении которых находится этот элемент.
a21
M 12
a31
a23
a33
62.
Алгебраические дополненияАлгебраическое дополнение Aik элемента
aik матрицы третьего порядка: число, равное
произведению минора этого элемента на (-1)i+k
.
Aik ( 1)
i k
M ik
63.
Пример 5 . Вычислить алгебраическое дополнениеэлемента a21 матрицы
2 1 0
A 1 3 1
2 0 1
Решение
1. Находим минор элемента a21:
2 1 0
i = 2;
A 1 3 1
k=1
2 0 1
1 0
М 21
( 1) 1 0 0 1
0 1
64.
Пример 5 . Вычислить алгебраическое дополнениеэлемента a21 матрицы
2 1 0
A 1 3 1
2 0 1
Решение
1. Находим минор элемента a21:
2 1 0
i = 2;
A 1 3 1
k=1
2 0 1
1 0
М 21
( 1) 1 0 0 1
0 1
2. Алгебраическое дополнение элемента a21:
A21 ( 1)2 1 M 21 ( 1) ( 1) 1
Aik ( 1)i k M ik
65.
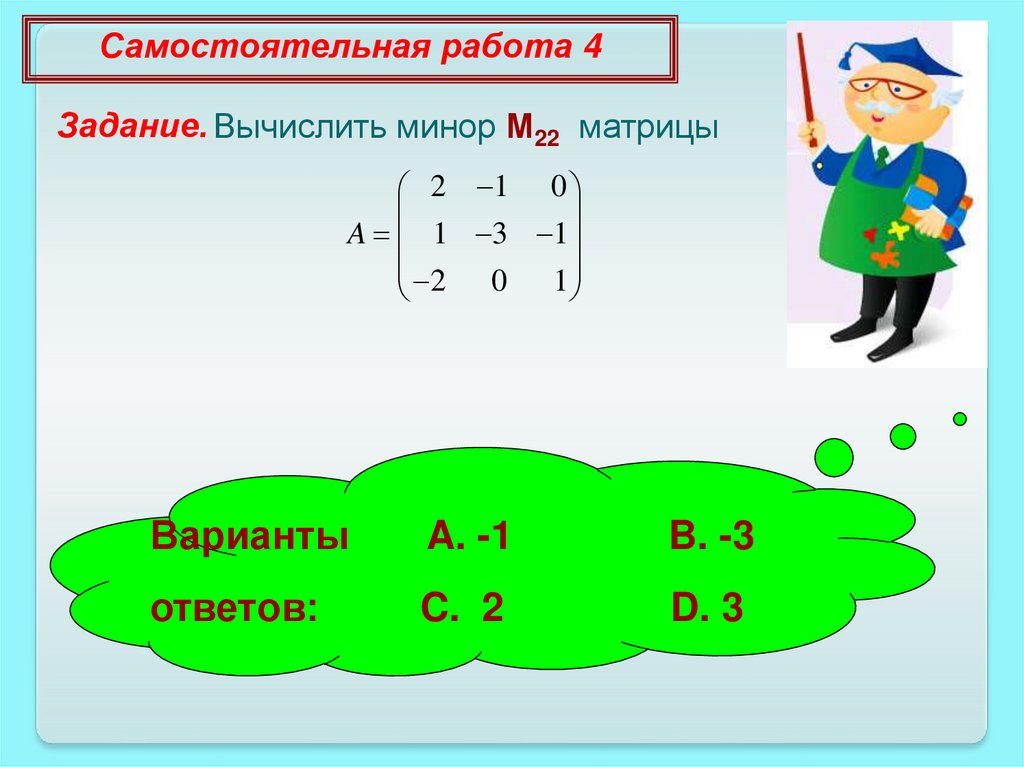
Самостоятельная работа 4Задание. Вычислить минор М22 матрицы
2 1 0
A 1 3 1
2 0 1
Варианты
A. -1
B. -3
ответов:
C. 2
D. 3
66.
Сверим ответы?Задание. Вычислить минор М22 матрицы
2 0
M 22
2 1 ( 2) 0 2
2 1
67.
Самостоятельная работа 5Задание. Вычислить алгебраическое
дополнение элемента a22
матрицы
2 1 0
A 1 3 1
2 0 1
Варианты
A. -2
B. -1
ответов:
C. 1
D. 2
68.
Сверим ответы?Вычислить алгебраическое
дополнение элемента a22
матрицы
2 0
M 22
2 1 ( 2) 0 2
2 1
A22 ( 1)2 2 M 22 1 2 2
69.
Определитель матрицы третьегопорядка
Это число, равное сумме произведений
элементов любой строки (столбца) матрицы на
их алгебраические дополнения
Например:
a11
a21
a31
a12
a22
a32
a13
a23 a11 A11 a12 A12 a13 A13
a33
- разложение определителя по первой строке
70.
a11 a12a21 a22
a31 a32
a13
a23 a13 A13 a23 A23 a33 A33
a33
- разложение определителя по третьему
столбцу
71.
Пример 6. Вычислить определитель матрицы Аразложением по первой строке
2 1 1
A 1 2 3
1 1 1
2 1 1
1 2 3 2 A11 ( 1) A12 1A 13
1 1 1
72.
Пример 6. Вычислить определитель матрицы Аразложением по первой строке
2 1 1
A 1 2 3
1 1 1
2 1 1
1 1 2 3
1 2 3 2 A11 ( 1) A12 1A 13 2( 1)
1 1
1 1 1
73.
Пример 6 . Вычислить определитель матрицы Аразложением по первой строке
2 1 1
A 1 2 3
1 1 1
2 1 1
1 1 2 3
1 2 3 2 A11 ( 1) A12 1A 13 2( 1)
1 1
1 1 1
1 2
( 1)( 1)
1 3
1 1
74.
Пример 6 . Вычислить определитель матрицы Аразложением по первой строке
2 1 1
A 1 2 3
1 1 1
2 1 1
1 1 2 3
1 2 3 2 A11 ( 1) A12 1A 13 2( 1)
1 1
1 1 1
1 2
( 1)( 1)
1 3
1 3 1 2
1( 1)
1 1
1 1
75.
Пример 6 . Вычислить определитель матрицы Аразложением по первой строке
2 1 1
A 1 2 3
1 1 1
2 1 1
1 1 2 3
1 2 3 2 A11 ( 1) A12 1A 13 2( 1)
1 1
1 1 1
1 2
( 1)( 1)
1 3
1 3 1 2
1( 1)
1 1
1 1
2 1 1 2 1( 1) 3.
76.
Пример 7. Вычислить определитель матрицыразложением по второму столбцу
2 1 1
A 1 2 3
1 1 1
2 1 1
1 2 3 ( 1) A12 2 A22 1 A 32
1 1 1
77.
Пример 7. Вычислить определитель матрицыразложением по второму столбцу
2 1 1
A 1 2 3
1 1 1
2 1 1
1 2 3 ( 1) A12 2 A22 1 A 32
1 1 1
1 2
( 1)( 1)
1 3
1 1
78.
Пример 7. Вычислить определитель матрицыразложением по второму столбцу
2 1 1
A 1 2 3
1 1 1
2 1 1
1 2 3 ( 1) A12 2 A22 1 A 32
1 1 1
1 2
( 1)( 1)
1
1 3
2 2 2
2( 1)
1 1
1 1
79.
Пример 7. Вычислить определитель матрицыразложением по второму столбцу
2 1 1
A 1 2 3
1 1 1
2 1 1
1 2 3 ( 1) A12 2 A22 1 A 32
1 1 1
1 2
( 1)( 1)
1
1
1 3
3 2 2
2 2 2
1( 1)
2( 1)
1 3
1 1
1 1
80.
Пример 7. Вычислить определитель матрицыразложением по второму столбцу
2 1 1
A 1 2 3
1 1 1
2 1 1
1 2 3 ( 1) A12 2 A22 1 A 32
1 1 1
1 2
( 1)( 1)
1
1
1 3
3 2 2
2 2 2
1( 1)
2( 1)
1 3
1 1
1 1
1 2 2 ( 3) ( 1) ( 7) 3.
81.
В Excelдля вычисления определителя матриц
используется функция
=МОПРЕД(Диапазон)
82.
Обратная матрица83.
Квадратная матрица А называется обратимой,если существует обратная к ней матрица A 1 ,
удовлетворяющая соотношениям
A A A A E
1
1
84.
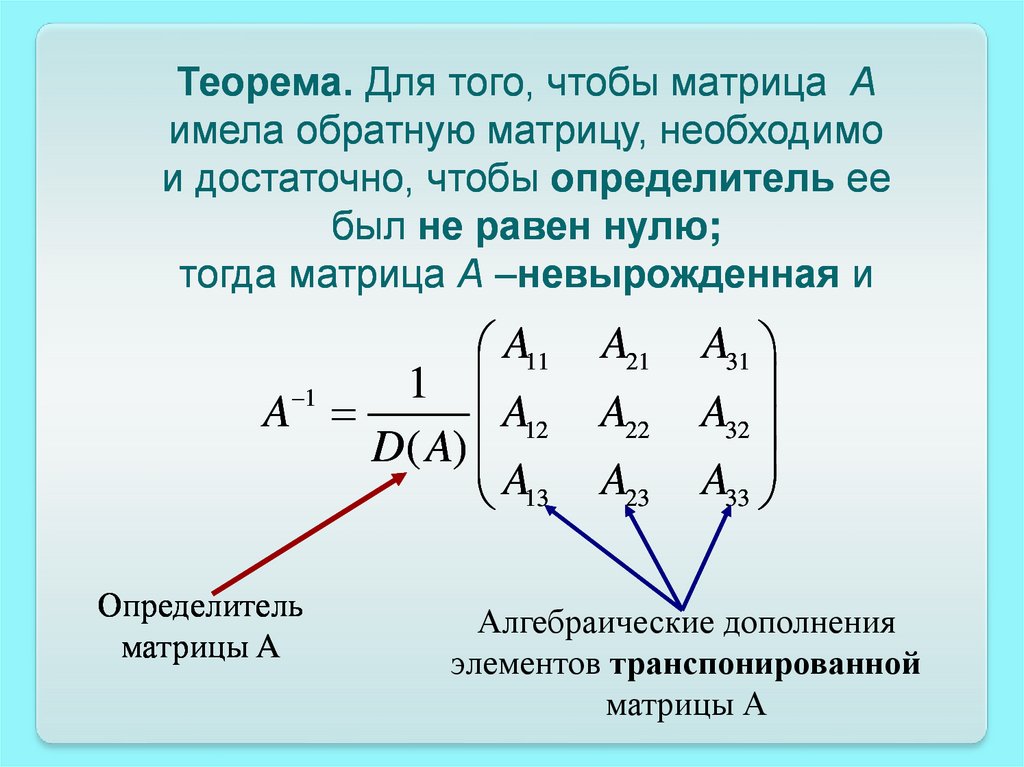
Теорема. Для того, чтобы матрица Аимела обратную матрицу, необходимо
и достаточно, чтобы определитель ее
был не равен нулю;
тогда матрица А –невырожденная и
A11
1
1
A
A
12
D( A)
A13
Определитель
матрицы A
A21
A22
A23
A31
A32
A33
85.
Теорема. Для того, чтобы матрица Аимела обратную матрицу, необходимо
и достаточно, чтобы определитель ее
был не равен нулю;
тогда матрица А –невырожденная и
A11
1
1
A
A
12
D( A)
A13
Определитель
матрицы A
A21
A22
A23
A31
A32
A33
Алгебраические дополнения
элементов транспонированной
матрицы А
86.
Пример 8. Дана матрица2 3
A
1 2
Найти матрицу, обратную А.
87.
1 A11A
A
D( A) 12
1
A21
A22
2 3
D( A)
4 ( 3) 1.
1 2
2 3
A
1 2
88.
1 A11A
A
D( A) 12
1
1 1
A11 ( 1)
( 2) 2
2 3
A
1 2
2 3
A
1 2
D( A) 1.
A21
A22
89.
1 A11A
A
D( A) 12
1
1 2
A12 ( 1)
1 1
2 3
A
1 2
D( A) 1.
A11 2
A21
A22
90.
1 A11A
A
D( A) 12
1
A21 ( 1)
2 1
A21
A22
( 3) 3
2 3
A
1 2
D( A) 1.
A11 2
A12 1
91.
Самостоятельная работа1 A11
A
D( A) A12
1
Задание
Определите значение алгебраического
дополнения А22
2 3
A
1 2
D( A) 1.
A11 2
A12 1
A21 3
A21
A22
92.
1 A11A
A
D( A) 12
1
A22 ( 1)
2 2
A21
A22
2 2
2 3
A
1 2
D( A) 1.
A11 2
A12 1
A21 3
93.
1 A11A
A
D( A) 12
1
A21
A22
D( A) 1.
A11 2
A12 1
A21 3
A22 2
1 2 3 2 3
A
1 1 2 1 2
1
2 3
A
1 2

















































































 mathematics
mathematics








