Similar presentations:
Глава 3. Линейная алгебра. §1. Матрицы
1.
2. Глава 3. Линейная алгебра
3. § 1. Матрицы
4.
Определение.Матрицей размера m n (или
числовой матрицей) называется
прямоугольная таблица,
образованная из mn чисел и
состоящая из m строк и n столбцов
(m, n N).
5.
Матрицы записывают в виде:a11 a12 ... a1n
a21 a22 ... a2n ,
.............................
am1 am 2 ... amn
a11 a12 ... a1n
a21 a22 ... a2n ,
.............................
a
a
...
a
mn
m2
m1
6.
a11 a12 ... a1na21 a22 ... a2n
,
.............................
am1 am2 ... amn
или более кратко: [aij], (aij), aij
соответственно.
7.
Числа aij (i 1, m, j 1, n) называютсяэлементами матрицы; ai1, ai2, …, ain
(i 1, m) – элементы i-й строки;
a1j, a2j, …, amj ( j 1, n) – элементы
j-го столбца. Матрицы обозначают:
A, B, C, … .
8.
Две матрицы A [aij] и B [bij]размера m n называются равными,
если aij bij (i 1, m, j 1, n); пишут:
A B.
9.
Нулевая матрица(обозначается О) – матрица размера
m n, все элементы которой равны
нулю.
10.
Матрица, состоящая из однойстроки, называется матрицейстрокой, а состоящая из одного
столбца – матрицей-столбцом.
Трапециевидной матрицей
называется матрица вида
11.
a11 a12 ... a1r ... a1n0 a22 ... a2r ... a2n
...........................................
0 0 ... arr ... arn ,
0 0 ... 0 ... 0
...........................................
0 0 ... 0 ... 0
где aii 0 (i 1, r ).
12.
Прямоугольной называетсяматрица размера m n, у которой
m n.
Матрица размера n n называется
квадратной порядка n.
13.
Главной диагональю квадратнойматрицы A [aij] порядка n
называется совокупность элементов
aii (i 1, n), а побочной диагональю –
совокупность элементов ai n–i+1
(i 1, n).
14.
Диагональной называетсяквадратная матрица, у которой все
элементы, расположенные вне
главной диагонали, равны нулю.
15.
Единичная матрица(обозначается Е) – диагональная
матрица, у которой все элементы,
стоящие на главной диагонали,
равны единице.
16.
Квадратная матрица называетсятреугольной, если все ее элементы,
расположенные по одну сторону от
главной диагонали, – нули.
17.
Если элементами матрицыявляются функции, то матрица
называется функциональной.
18.
19. § 2. Операции над матрицами
20.
Определение.Суммой матриц A [aij] и B [bij]
размеров m n называется матрица
A + B [aij + bij] размера m n
(i 1, m, j 1, n).
21.
Определение.Произведением матрицы A [aij]
размера m n на число λ (λ R)
называется матрица λA [λaij]
размера m n (i 1, m, j 1, n).
22.
Матрица –A (–1)A называетсяпротивоположной матрице A.
Разностью матриц A и B
называется матрица A – B A + (–B).
23.
Определение.Произведением матрицы A [aik]
размера m n на матрицу B [bkj]
размера n p называется матрица
AB [ai1b1j + ai2b2j + ai3b3j +…+ ainbnj]
размера m p (i 1, m, k 1, n, j 1, p).
24.
Операция произведения матрицA и B определена для согласованных
матриц, т.е. когда количество
столбцов матрицы A равно
количеству строк матрицы B.
25.
Если AB BA, то матрицы A и Bназываются перестановочными (или
коммутирующими).
26.
Определение.k-й степенью (k N) квадратной
матрицы A называется матрица Ak
k
такая, что A AA...A .
k раз
По определению, A0 E.
27.
Операции над матрицамиобладают свойствами:
1) A + B B + A,
2) (A + B) + C A + (B + C),
3) λ(μA) (λμ)A (λ, μ R),
4) (λ + μ)A (λA + μA) (λ, μ R),
28.
5) λ(A + B) = λA + λB (λ R),6) A(BC) (AB)C,
7) A(B + C) AB + AC.
29.
Определение.Матрицей, транспонированной по
отношению к матрице A [aij]
размера m n называется матрица
AT [aji] размера n m.
30.
Переход от A к AT называетсятранспонированием.
31.
Операция транспонированияобладает свойствами:
1) (AT)T = A,
2) (λA)T λAT (λ R),
3) (A + B)T AT + BT,
4) (AB)T BTAT.
32.
33. § 3. Определители
34.
Если A [a11], то определителемпервого порядка называется число
a11.
35.
Определение.a11
Если A
a
21
a12
, то
a22
определителем второго порядка
называется число
36.
a11 a12a11a22 a12a21.
a21 a22
37.
Определение.a11 a12
Если A a21 a22
a
a
31
32
a13
a23 , то
a33
определителем третьего порядка
называется число
38.
a11 a12 a13a22 a23
a21 a23
a21 a22
a21 a22 a23 a11
a12
+ a13
.
a32 a33
a31 a33
a31 a32
a31 a32 a33
39.
Для вычисления определителятретьего порядка можно
использовать правило
треугольников:
40.
a11 a12 a13a21 a22 a23 a11a22a33 + a12a23a31 +
a31 a32 a33
+ a13a21a32 – a13a22a31 – a12a21a33 –
– a11a23a32.
41.
42.
Если A [aij] (i, j 1, n, n N), тоопределитель n-го порядка
записывают в виде
43.
a11 a12 ... a1na21 a22 ... a2n
,
.............................
an1 an 2 ... ann
где aij (i, j 1, n) называются
элементами определителя.
44.
Определитель матрицы Aобозначают: Δ, detA, |A|.
45.
Определение.Минором Mij элемента aij
определителя n-го порядка (n > 1)
называется определитель (n –1)-го
порядка, полученный из исходного
вычеркиванием i-й строки и j-го
столбца.
46.
Определение.Алгебраическим дополнением Aij
элемента aij определителя n-го
порядка называется число
Aij (–1)i+jMij.
47.
Определитель n-го порядкаматрицы A [aij] можно вычислять:
1) путем разложения по
элементам i-й строки:
n
ai1 Ai1 + ai 2 Ai 2 + ... + ain Ain aik Aik ;
k 1
48.
2) путем разложением поэлементам j-го столбца:
n
a1 j A1 j + a2 j A2 j + ... + anj Anj akj Akj .
k 1
49.
Определители обладаютследующими свойствами:
1) если все элементы какоголибо ряда определителя равны
нулю, то определитель равен
нулю;
50.
2) при перестановке двух строк(столбцов) определитель изменит
знак на противоположный;
3) определитель, содержащий две
одинаковых строки (столбца), равен
нулю;
51.
4) если все элементы некоторойстроки (столбца) определителя
умножить на число k (k R), то
исходный определитель умножится
на это число;
52.
5) если соответствующиеэлементы двух строк (столбцов)
определителя пропорциональны, то
он равен нулю;
53.
6) определитель не изменится,если к элементам какой-либо строки
(столбца) прибавить
соответствующие элементы другой,
умноженной на одно и то же число;
54.
Справедливы формулы:|AB| |A||B|,
|An| |A|n (n N),
|AT| |A|.
55.
56. § 4. Обратная матрица
57.
Квадратная матрица А называетсяневырожденной (или неособенной)
если |A| 0. В противном случае A –
вырожденная (или особенная).
58.
Определение.Матрица A–1 называется обратной
матрицей для квадратной матрицы
А, если
AA–1 A–1A E,
где E – единичная матрица.
59.
Теорема.Матрица А имеет обратную тогда
и только тогда, когда матрица А –
невырожденная.
60.
Если A [aij] (i, j 1, n), тоA11 A21 ... An1
1 A12 A22 ... An 2
1
A
,
A .............................
A1n A2n ... Ann
61.
где |A| – определитель матрицы А,Aij – алгебраические дополнения
элементов aij матрицы А.
62.
Обратная матрица обладаетсвойствами:
1
1
1) A ,
A
2) (A–1)–1 A,
63.
3) (AB)–1 B–1A–1,4) (Ak)–1 (A–1)k (k N),
5) (AT)–1 (A–1)T.
64.
65. § 5. Ранг матрицы
66.
Определение.Рангом матрицы называется
наивысший порядок отличных от
нуля ее миноров.
Ранг матрицы A обозначают:
r(A), rA, rank A.
67.
Базисным минором матрицыназывается любой отличный от нуля
минор порядка r r(A).
68.
Метод окаймляющих миноров.Если в матрице A найден ненулевой
минор Mk порядка k (k N), а все
окаймляющие его миноры (k +1)-го
порядка равны нулю, то ранг
матрицы A равен k.
69.
70. § 6. Системы линейных алгебраических уравнений
71.
Определение.Системой m линейных
алгебраических уравнений с n
неизвестными x1, x2, …, xn
называется система вида
72.
a11 x1 + a12 x2 + ... + a1n xn b1,a21x1 + a22 x2 + ... + a2 n xn b2 ,
.............................................
am1 x1 + am 2 x2 + ... + amn xn bm ,
73.
где aij (i 1, m, j 1, n) –коэффициенты системы; bi (i 1, m) –
свободные члены; m, n N.
74.
Решением системы называетсясовокупность n значений
неизвестных, удовлетворяющих
одновременно всем уравнениям
системы.
75.
Система уравнений называетсясовместной, если она имеет хотя бы
одно решение. В противном случае
система называется несовместной.
76.
Система называетсяопределенной, если она имеет
единственное решение.
77.
Решить систему – значитопределить, совместна она или нет,
и в случае совместности найти
множество всех ее решений.
78.
Матрицаa11 a12 ... a1n
a21 a22 ... a2n
A
.............................
am1 am 2 ... amn
называется матрицей (или основной
матрицей) системы.
79.
Матрицаa11 a12 ... a1n b
1
a21 a22 ... a2n b2
[ A B]
............................. ...
am1 am 2 ... amn bm
называется расширенной матрицей
системы
80.
Теорема Кронекера – Капелли.Система линейных алгебраических
уравнений совместна тогда и только
тогда, когда r(A) r([A|B]).
81.
Определение.Определителем системы n
линейных уравнений с n
неизвестными называется
определитель Δ матрицы этой
системы.
82.
Если Δ 0, то система имеетединственное решение и называется
невырожденной.
Если Δ 0, то система не имеет
решения или имеет бесконечное
множество решений и называется
вырожденной.
83.
Для решения невырожденнойсистемы используют метод Крамера
и метод обратной матрицы.
84.
Метод Крамера. Необходимо:1) вычислить определитель Δ
системы;
2) в определителе Δ заменить
поочередно i-й столбец столбцом
свободных членов и вычислить
соответствующие определители Δi ;
85.
3) вычислить значенияx1, x2, …, xn по формулам Крамера:
1
2
n
x1 , x2 , ..., xn ;
4) записать решение (x1, x2,…, xn).
86.
Метод обратной матрицы.Необходимо:
1) записать систему в матричном
виде: AX B, где A – матрица
системы, X – матрица-столбец
неизвестных, B – матрица-столбец
свободных членов;
87.
2) решить матричное уравнениеX A–1B;
3) записать решение (x1, x2,…, xn).
88.
Основным методом решенияпроизвольных систем является
метод Гаусса. Он базируется на
понятии элементарных
преобразований строк матрицы
системы.
89.
Элементарнымипреобразованиями строк матрицы
называются:
1) перестановка строк;
2) умножение строки на одно и то
же число λ (λ
0);
90.
3) прибавление к строке матрицыдругой строки, умноженной на
некоторое число.
В результате элементарных
преобразований строк матрицы A
получают эквивалентную матрицу
B; пишут: A ~ B.
91.
Метод Гаусса. Необходимо:1) записать расширенную
матрицу системы;
2) с помощью элементарных
преобразований строк расширенной
матрицы свести матрицу системы к
треугольной или трапециевидной;
92.
3) для преобразованной такимобразом расширенной матрицы
записать соответствующую систему
уравнений;
4) решить полученную систему
начиная с последнего уравнения;
5) записать решение (x1, x2,…, xn).
93.
В истории черпаем мымудрость, в поэзии –
остроумие, в математике
– проницательность.
Ф. Бэкон



































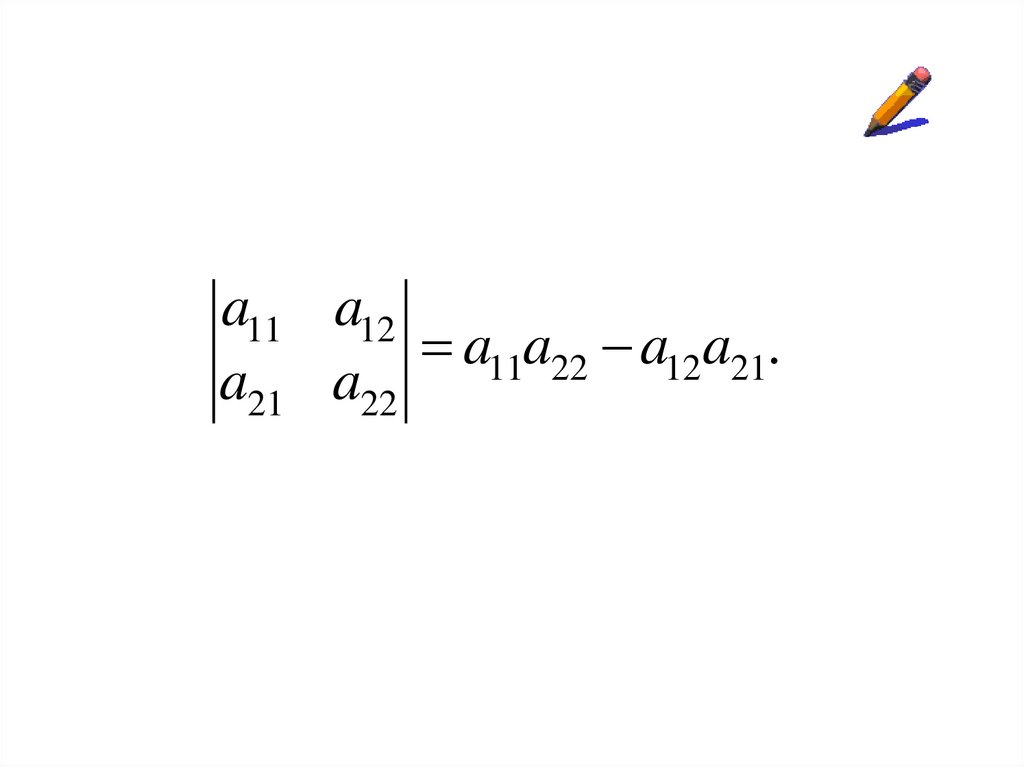

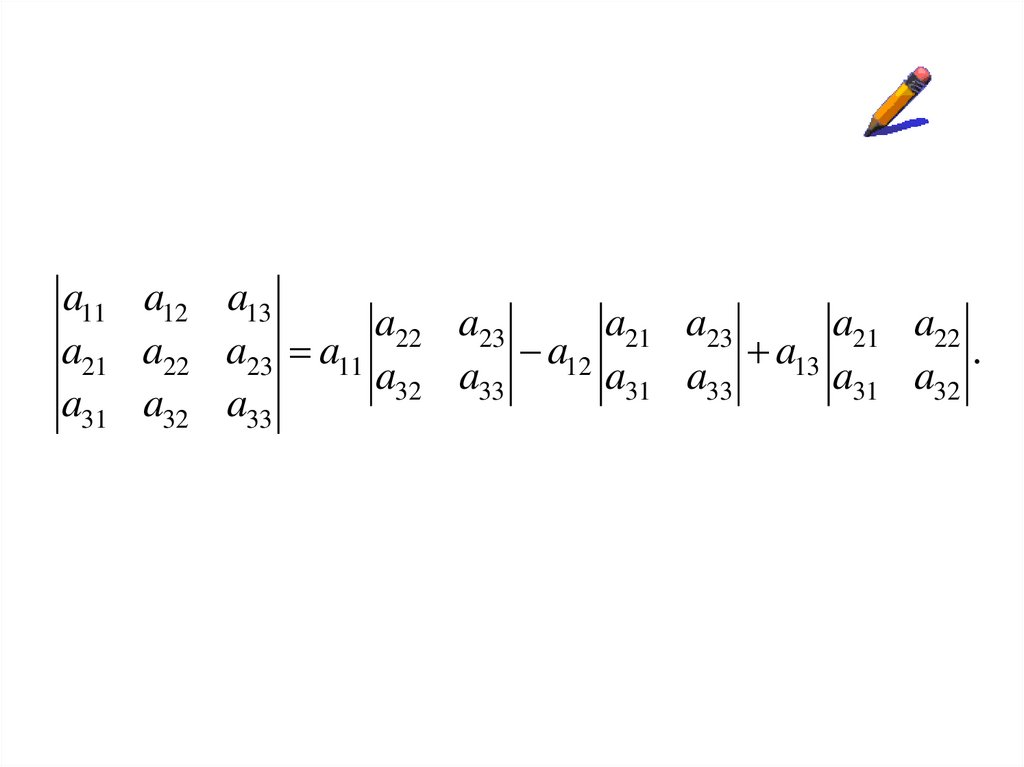
























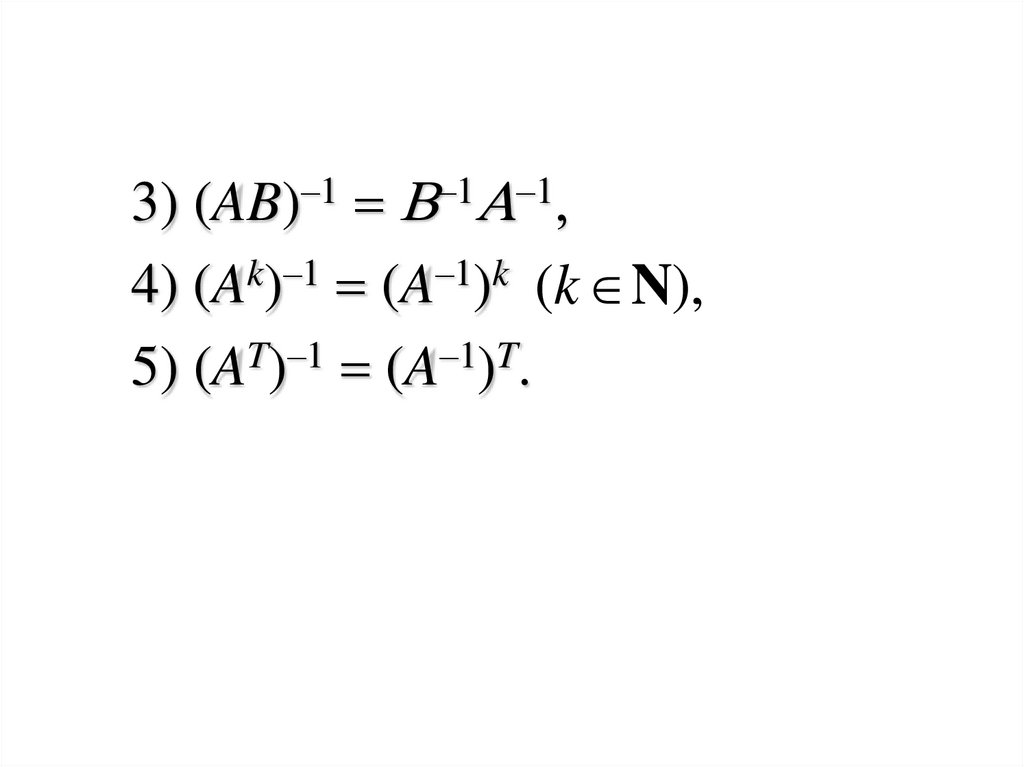






























 mathematics
mathematics








