Теорема о трёх перпендикулярах

1.

Теорема о трёх перпендикулярах.

2.

«Есть истины, как страны,
наиболее удобный путь к
которым становится известным
лишь после того, как мы
испробуем все пути.… На пути к
истине мы почти всегда
обречены совершать ошибки»
Дени Дидро.

3. Теоретический опрос

1. Угол между прямыми равен 90˚. Как называются
такие прямые?
Ответ: перпендикулярные.
2. Верно ли утверждение: «Прямая называется
перпендикулярной плоскости, если она
перпендикулярна некоторой прямой, лежащей этой
плоскости»
Ответ: да.
3. Продолжите предложение: «Прямая
перпендикулярна плоскости, если она...»
Ответ: перпендикулярна к двум пересекающимся
прямым, лежащим в этой плоскости.

4.

4. Что можно сказать о двух (3-х, 4-х) прямых,
перпендикулярных к одной плоскости?
Ответ: они параллельны.
5. Две прямые, перпендикулярные третьей прямой, …
Ответ: параллельны.
6. Как определяется расстояние от точки до прямой на
плоскости?
Ответ: как длина перпендикуляра, проведённого из точки к
данной прямой.
7. Как называются отрезки:
АМ - ?; АН -?;
Точка М -?; Точка Н -?.
А
Ответ: АМ – наклонная, АН- перпендикуляр,
М- основание наклонной,
Н - основание перпендикуляра
М
α
Н

5.

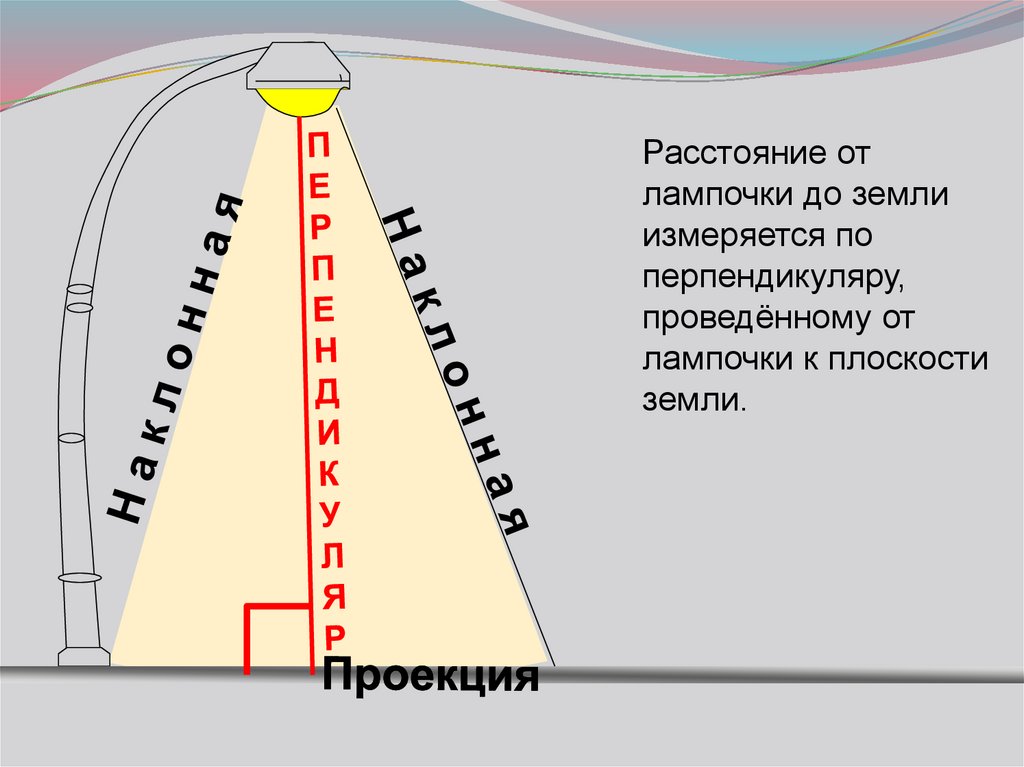
Расстояние от
лампочки до земли
измеряется по
перпендикуляру,
проведённому от
лампочки к плоскости
земли.

6.

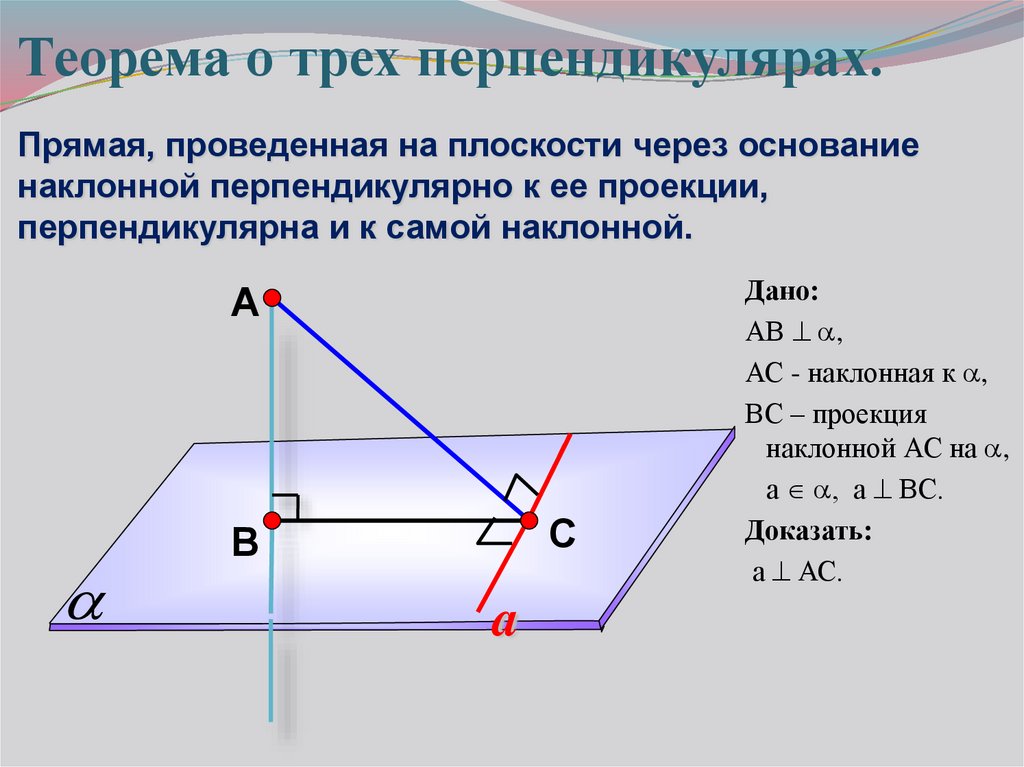
Теорема о трех перпендикулярах.
Прямая, проведенная на плоскости через основание
наклонной перпендикулярно к ее проекции,
перпендикулярна и к самой наклонной.
А
С
В
a
Дано:
АВ ,
АС - наклонная к ,
ВС – проекция
наклонной АС на ,
а , а ВС.
Доказать:
а АС.

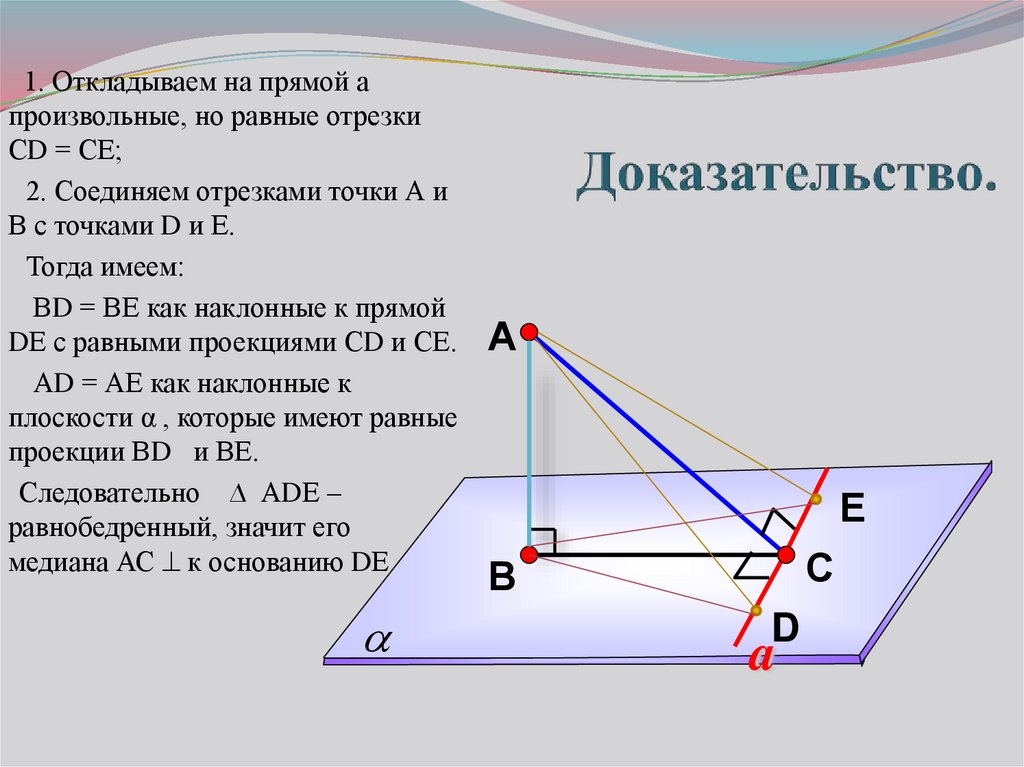
7. Доказательство.

1. Откладываем на прямой а
произвольные, но равные отрезки
СD = СЕ;
2. Соединяем отрезками точки А и
В с точками D и Е.
Тогда имеем:
ВD = ВЕ как наклонные к прямой
DЕ с равными проекциями СD и СЕ.
АD = АЕ как наклонные к
плоскости α , которые имеют равные
проекции ВD и ВЕ.
Следовательно ∆ АDЕ –
равнобедренный, значит его
медиана АС к основанию DЕ.
А
Е
С
В
D
a

8.

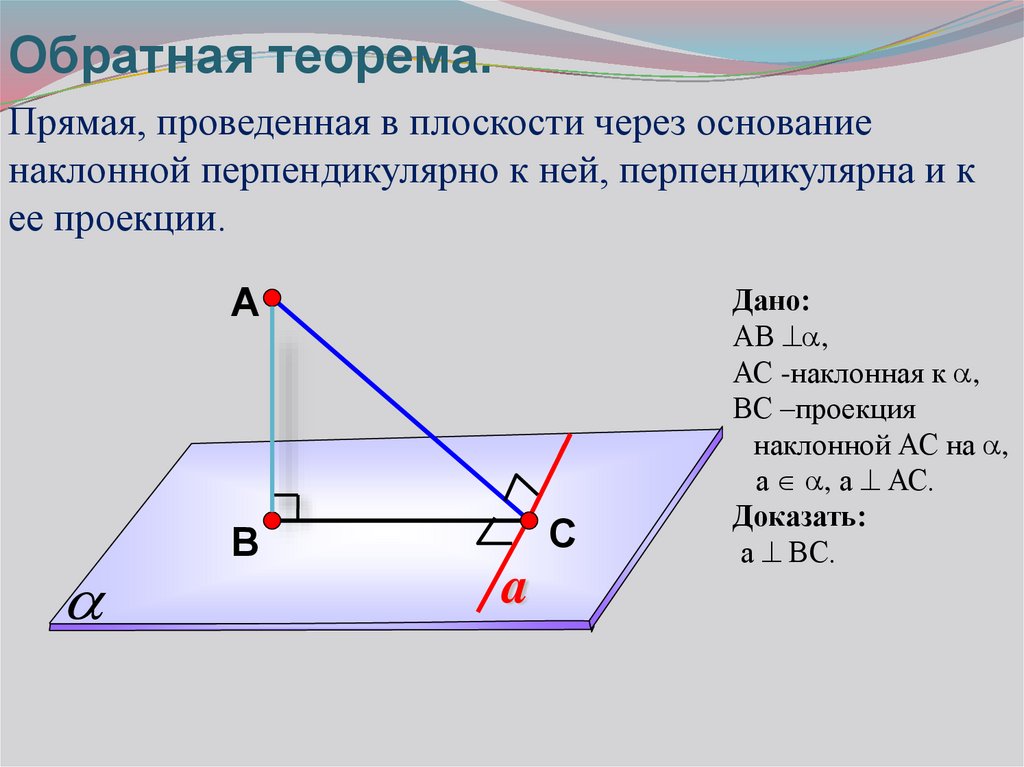
Обратная теорема.
Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ней, перпендикулярна и к
ее проекции.
А
С
В
a
Дано:
АВ ,
АС -наклонная к ,
ВС –проекция
наклонной АС на ,
а , а АС.
Доказать:
а ВС.

9.

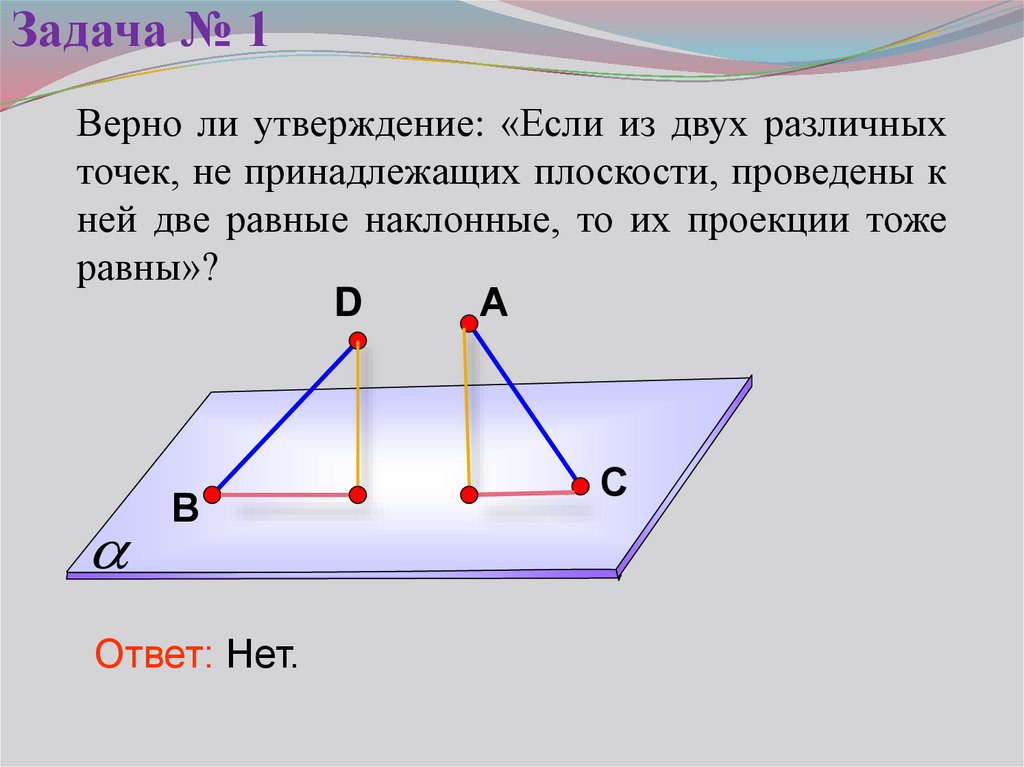
Задача № 1
Верно ли утверждение: «Если из двух различных
точек, не принадлежащих плоскости, проведены к
ней две равные наклонные, то их проекции тоже
равны»?
D
А
В
Ответ: Нет.
С

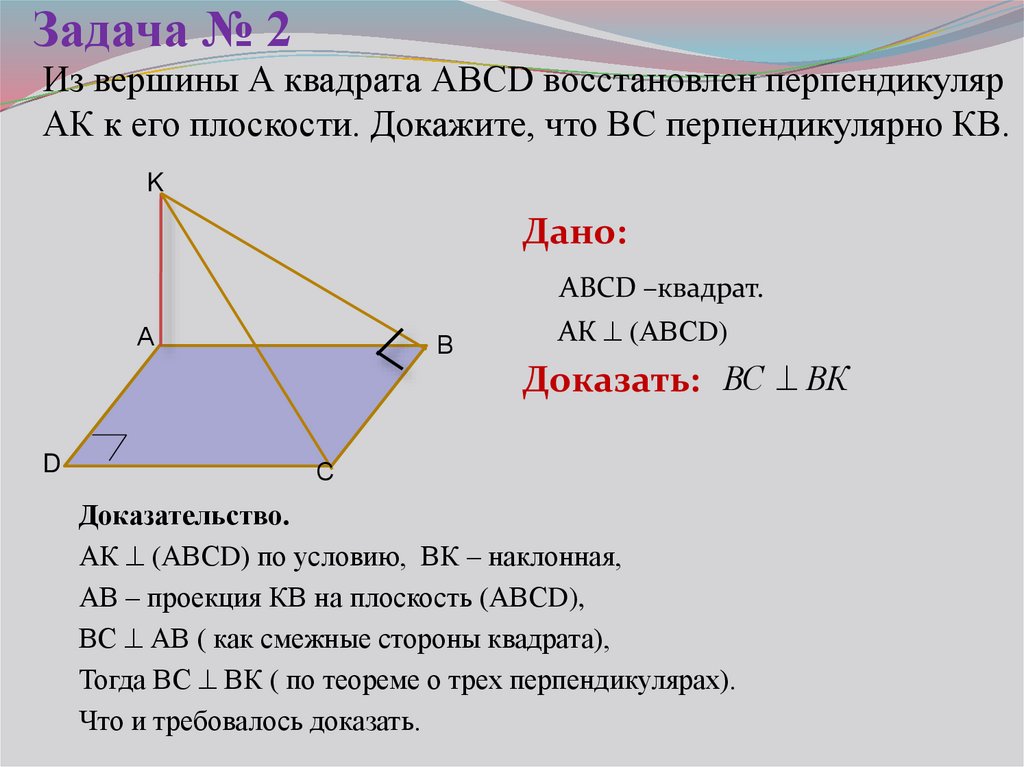
10. Задача № 2

Из вершины А квадрата АВСD восстановлен перпендикуляр
АК к его плоскости. Докажите, что ВС перпендикулярно КВ.
K
Дано:
АВСD –квадрат.
А
D
В
АК (АВСD)
Доказать: ВС ВК
С
Доказательство.
АК (АВСD) по условию, ВК – наклонная,
АВ – проекция КВ на плоскость (АВСD),
ВС АВ ( как смежные стороны квадрата),
Тогда ВС ВК ( по теореме о трех перпендикулярах).
Что и требовалось доказать.

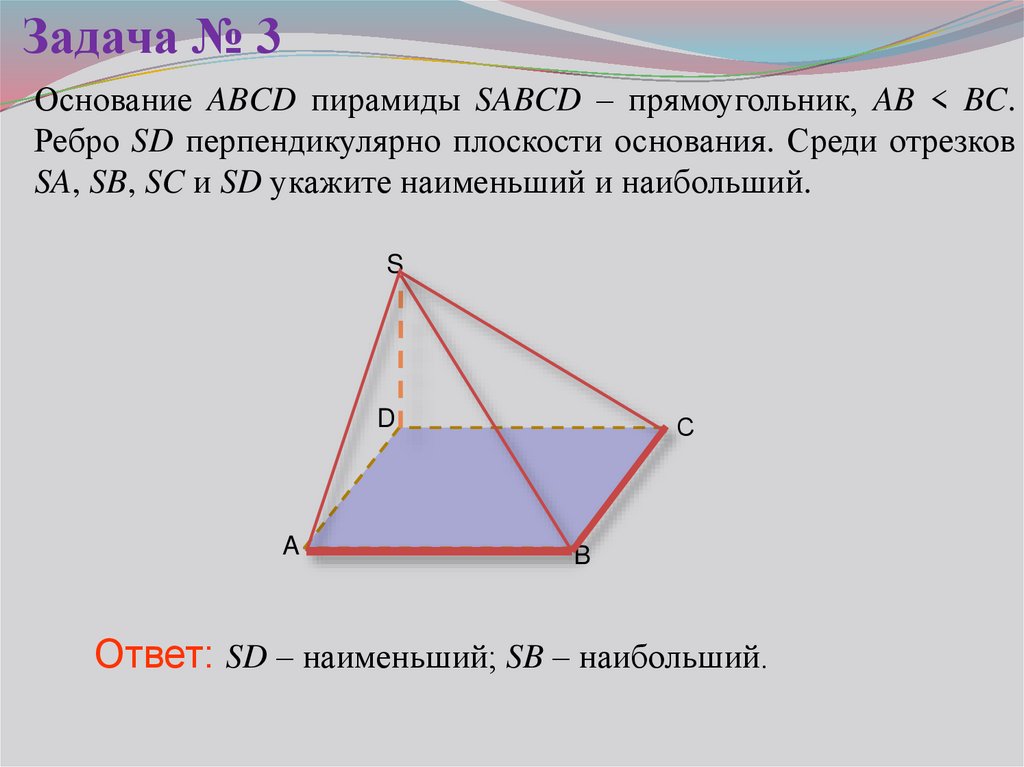
11. Задача № 3

Основание ABCD пирамиды SABCD – прямоугольник, AB < BC.
Ребро SD перпендикулярно плоскости основания. Среди отрезков
SA, SB, SC и SD укажите наименьший и наибольший.
S
D
A
С
B
Ответ: SD – наименьший; SB – наибольший.

12.

Самостоятельное выполнение заданий
1. Верно ли, что две прямые, перпендикулярные к одной
2.
3.
4.
5.
6.
7.
плоскости, параллельны.
Может ли прямая, перпендикулярная к плоскости, быть
параллельна прямой, лежащей в этой плоскости?
Верно ли, что прямая перпендикулярна к плоскости, если
она перпендикулярна к двум прямым этой плоскости?
Могут ли две пересекающиеся прямые быть
перпендикулярными к одной плоскости?
Верно ли, что две прямые в пространстве,
перпендикулярные к третьей прямой, параллельны?
Могут ли пересекаться две плоскости, параллельные к
одной прямой ?
Верно ли, длина перпендикуляра меньше длины проекции
наклонной, проведенной из той же точки?

13.

1. п. 20 стр 42
2. № 153