Теорема о трёх перпендикулярах

1.

2.

АВ — перпендикуляр
к плоскости
АC — наклонная
CB — проекция
АB — расстояние
от точки до плоскости
A
C
B
α

3.

A
C
B
α

4.

Теорема
Если в плоскости провести прямую через
основание наклонной перпендикулярно
к её проекции на данную плоскость, то эта
прямая будет перпендикулярна и к самой
наклонной

5.

Теорема
Если в плоскости провести прямую через основание наклонной
перпендикулярно к её проекции на данную плоскость, то эта прямая
будет перпендикулярна и к самой наклонной
Дано:
A
AB ⏊ α
АС — наклонная к α
ВС — проекция АС
СD ∈ α, CD ⏊ BC
Доказать: CD ⏊ AC
Доказательство:
1) CD ⏊ BC
AB ⏊ α ⇒ AB ⏊ CD
2) CD ⏊ AB, CD ⏊ BC
AB, BC ∈ (ABC) ⇒
⇒ CD ⏊ (ABC)
D
B
α
Теорема о трёх
перпендикулярах
C
⇒ CD ⏊ AC
По признаку перпендикулярности
прямой и плоскости
Теорема доказана

6.

Обратная теорема
Если провести прямую в плоскости через
основание наклонной перпендикулярно
к ней, то данная прямая будет
перпендикулярна и к её проекции

7.

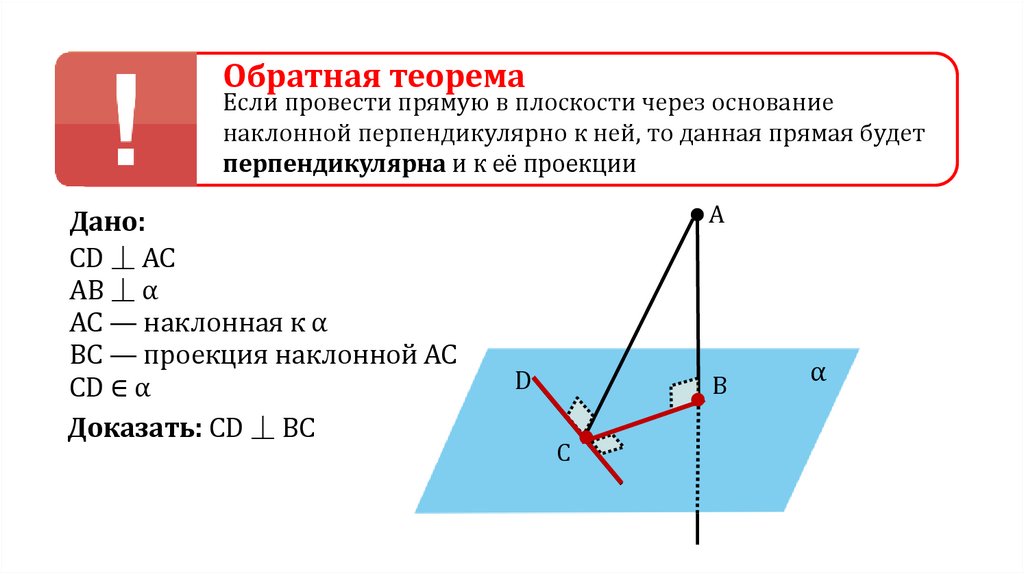
Обратная теорема
Если провести прямую в плоскости через основание
наклонной перпендикулярно к ней, то данная прямая будет
перпендикулярна и к её проекции
Дано:
CD ⏊ AC
AB ⏊ α
АС — наклонная к α
ВС — проекция наклонной АС
СD ∈ α
Доказать: CD ⏊ BC
A
D
B
C
α

8.

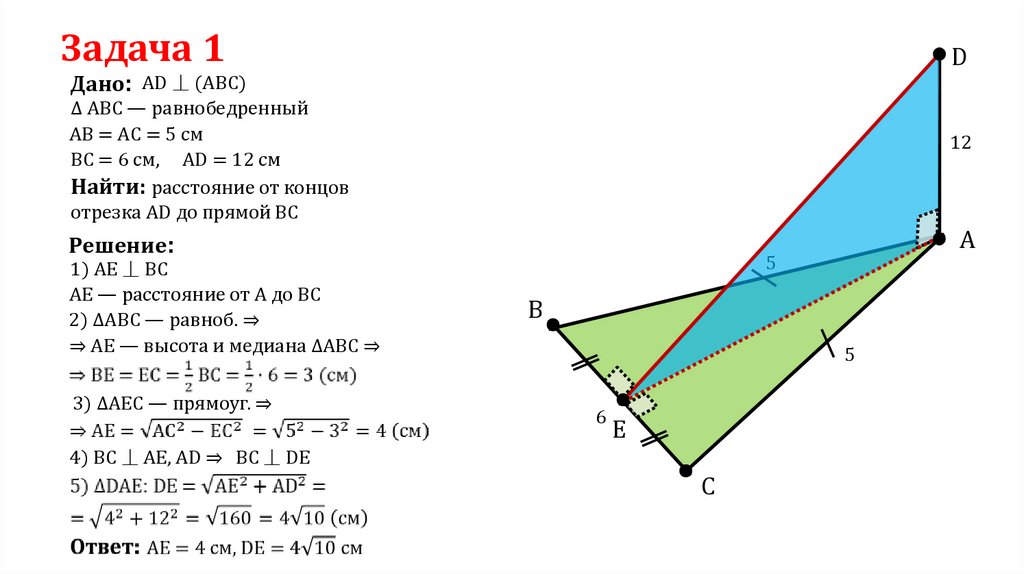
Задача 1
D
Дано: AD ⏊ (ABC)
∆ ABC — равнобедренный
AB = АC = 5 см
ВС = 6 см, AD = 12 см
Найти: расстояние от концов
отрезка AD до прямой ВС
12
Решение:
1) AE ⏊ BC
AE — расстояние от А до BC
2) ΔАВС — равноб. ⇒
⇒ АЕ — высота и медиана ΔАВС ⇒
3) ∆АЕС — прямоуг. ⇒
A
5
B
5
6
E
4) BC ⏊ AE, AD ⇒ BC ⏊ DE
C

9.

Задача 2
Дано: BD ⏊ (ABC)
D
ВD = 9 см, АС = 10 см
ВС = ВА = 13 см
Найти:
a) расстояние от точки D
до прямой AС
б) SACD
9
Решение:
1) BE ⏊ AC
2) ΔАВС: BЕ — высота и медиана ΔАВС ⇒
⇒ СЕ = ЕА = 5 см
3) BD ⏊ AC, ВЕ ⏊ АС ⇒ DЕ ⏊ АС
A
13
B
E
13
5) ∆ACD: AC — основание, DE — высота ⇒
Ответ: DE = 15 см, SACD = 75 см2
C
10