Similar presentations:
Угол между прямой и плоскостью. Теорема о трёх перпендикулярах
1.
2.
АПОВТОРИТЕ!
С
В
1. Назовите гипотенузу прямоугольного треугольника АВС.
2. Сравните катет и гипотенузу прямоугольного треугольника.
Что больше и почему?
3.
Сформулируйте теорему Пифагора.
4.
Какие прямые называются перпендикулярными?
5. Верно ли утверждение: «прямая перпендикулярна плоскости,
если она перпендикулярна некоторой прямой, лежащей в
этой плоскости».
6. Продолжи предложение: «Прямая перпендикулярна
плоскости, если она . . . »
3.
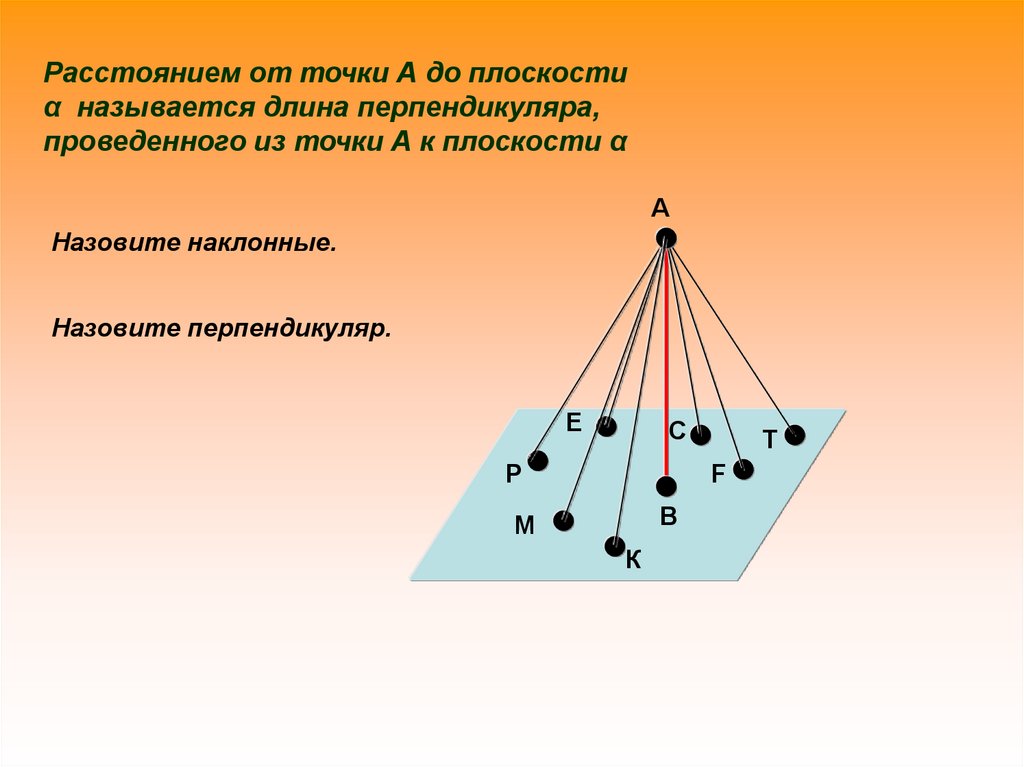
Расстоянием от точки А до плоскостиα называется длина перпендикуляра,
проведенного из точки А к плоскости α
А
Назовите наклонные.
Назовите перпендикуляр.
Е
С
Р
Т
F
В
М
К
4.
Угол между прямой и плоскостью.Углом между прямой и плоскостью, пересекающей
эту прямую и не перпендикулярную к ней, называется
угол между прямой и ее проекцией на плоскость.
а
а1
А
5.
аа
А
Если
а , то проекция
является точка А.
на
а1
(а, ) 90
а
Если
а1
а , то прямая
проекция прямой
на плоскость
а а1 , (а, ) 0
а
6.
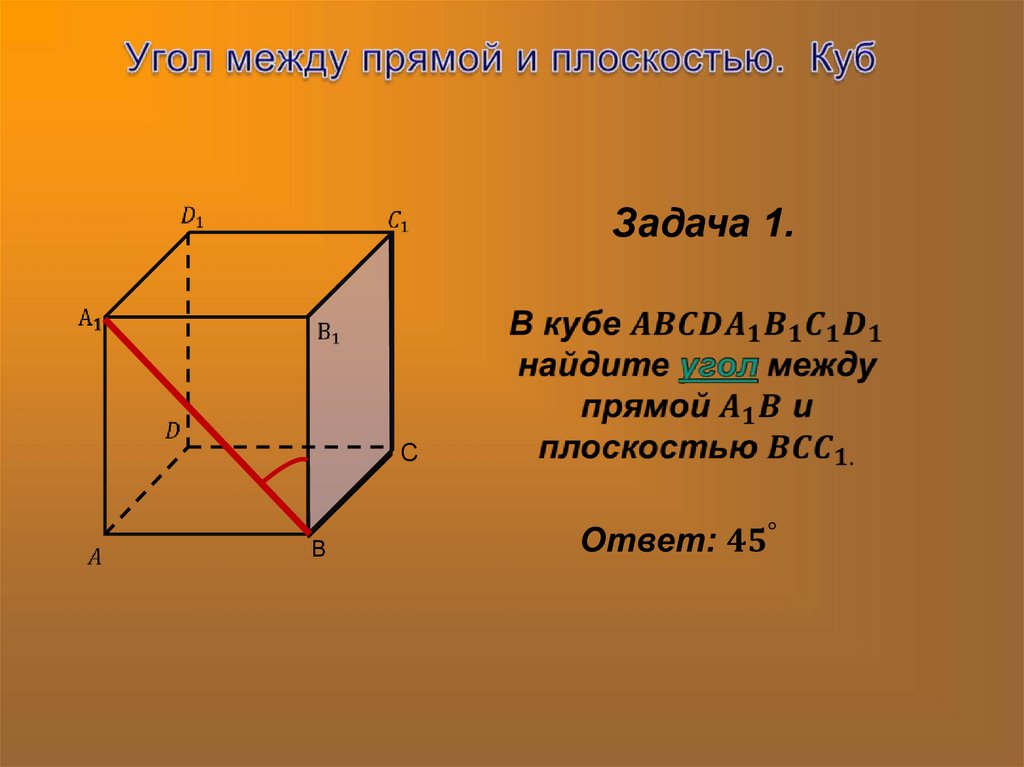
Задача 1.C
B
7.
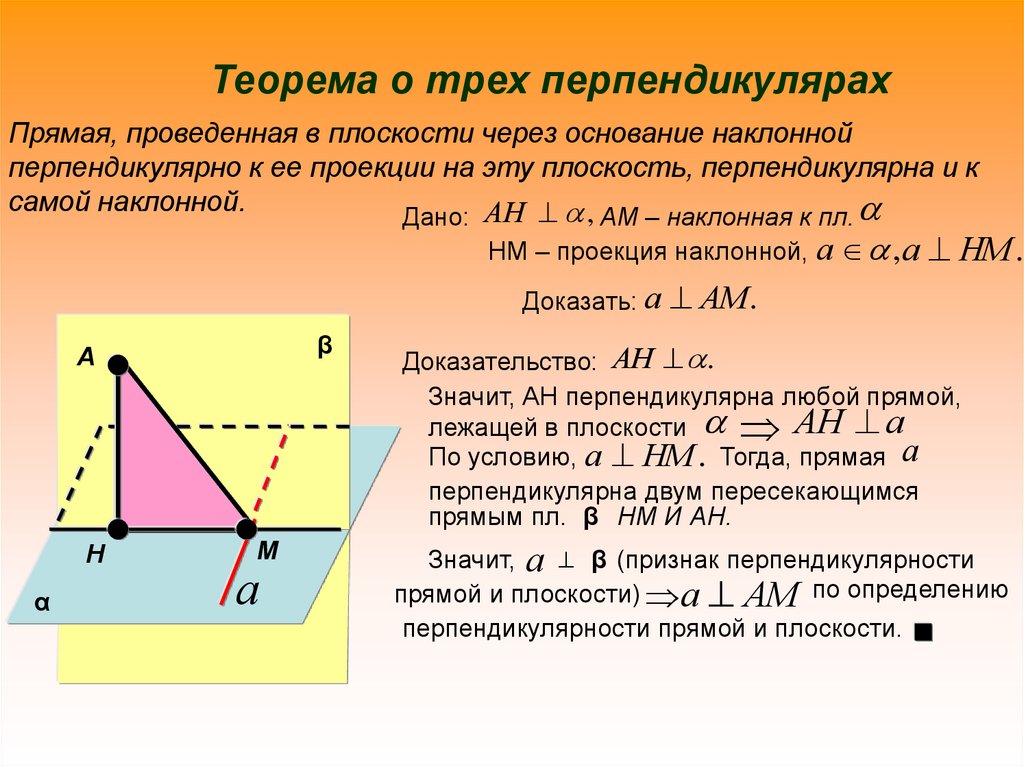
Теорема о трех перпендикулярахПрямая, проведенная в плоскости через основание наклонной
перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к
самой наклонной.
АН ,
Дано:
АМ – наклонная к пл.
НМ – проекция наклонной, а , а
Доказать: а
β
А
Н
α
М
а
НМ .
АМ.
Доказательство: АН .
Значит, АН перпендикулярна любой прямой,
лежащей в плоскости АН а
По условию, а НМ . Тогда, прямая а
перпендикулярна двум пересекающимся
прямым пл. β НМ И АН.
Значит, а β (признак перпендикулярности
прямой и плоскости) а АМ по определению
перпендикулярности прямой и плоскости.
8.
Теорема обратная теореме о трехперпендикулярах
Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ней , перпендикулярна
и к её проекции.
9. Задача на построение
Отрезок МС перпендикулярен плоскости равностороннеготреугольника АВС.
Проведите через точку М перпендикуляр к прямой АВ.
Дано: ∆АВС – равносторонний,
МС (АВС).
Построить: МЕ┴ АВ
М
Построение:
1. ∆АВС: проведём СЕ ┴ АВ.
2. Проведём МЕ.
МЕ ┴ АВ – по теореме о трёх
перпендикулярах.
С
А
Е
B
10. Задача на доказательство
B1C1
A1
D1
B
A
C
O
D
Дано: АВСDA1B1C1D1– куб.
Доказать: АС ОВ1
Доказательство:
ВВ1 – перпендикуляр;
ОВ1 – наклонная;
ОВ – проекция наклонной;
АС – прямая (через основание наклонной)
(Если АС ОВ, то АС ОВ1)
1)АВСD – квадрат, значит, АС BD
– по свойству диагоналей квадрата;
2) АС ОВ, значит, АС
ОВ1 – по
теореме о трёх перпендикулярах, ч.т.д.
11.
Домашнее задание12.
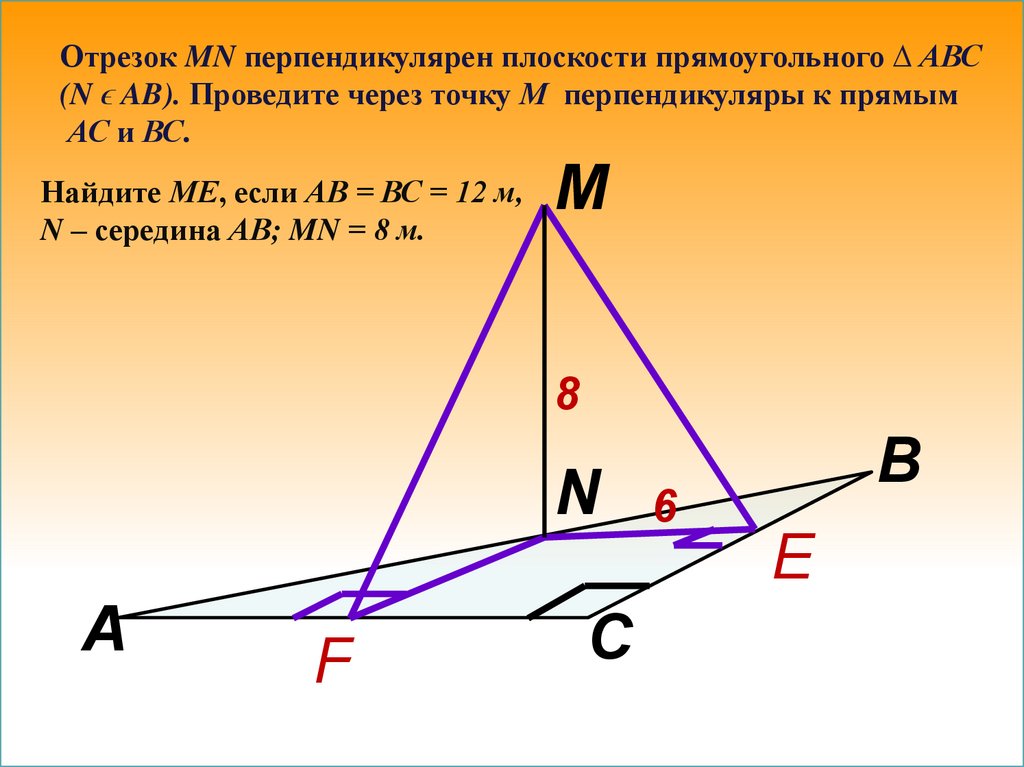
Отрезок MN перпендикулярен плоскости прямоугольного ∆ АВС(N ϵ AB). Проведите через точку М перпендикуляры к прямым
АС и ВС.
Найдите МЕ, если АВ = ВС = 12 м,
N – середина АВ; MN = 8 м.
M
8
N
B
6
E
A
F
C








 mathematics
mathematics








