Similar presentations:
Теорема о трех перпендикулярах
1. Устная работа
Тема: Теорема о трех перпендикулярах.2.
1. Верно ли утверждение: «прямая называетсяперпендикулярной плоскости, если она
перпендикулярна некоторой прямой, лежащей этой
плоскости»
2.
На практике вертикальность столба проверяют, глядя
на столб поочередно с двух направлений. Как
обосновать правильность такой проверки?
3.
Могут ли быть перпендикулярны к плоскости две
стороны треугольника одновременно?
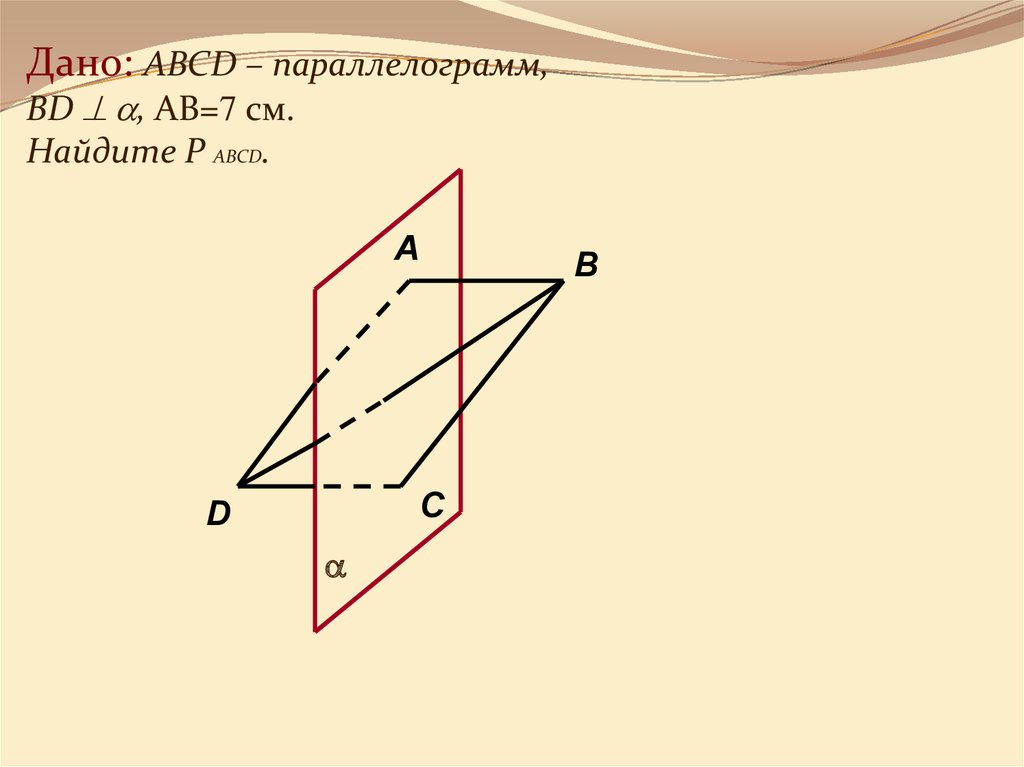
3. Дано: ABCD – параллелограмм, BD , АВ=7 см. Найдите Р АВCD.
Дано: ABCD – параллелограмм,BD , АВ=7 см.
Найдите Р АВCD.
A
B
C
D
4.
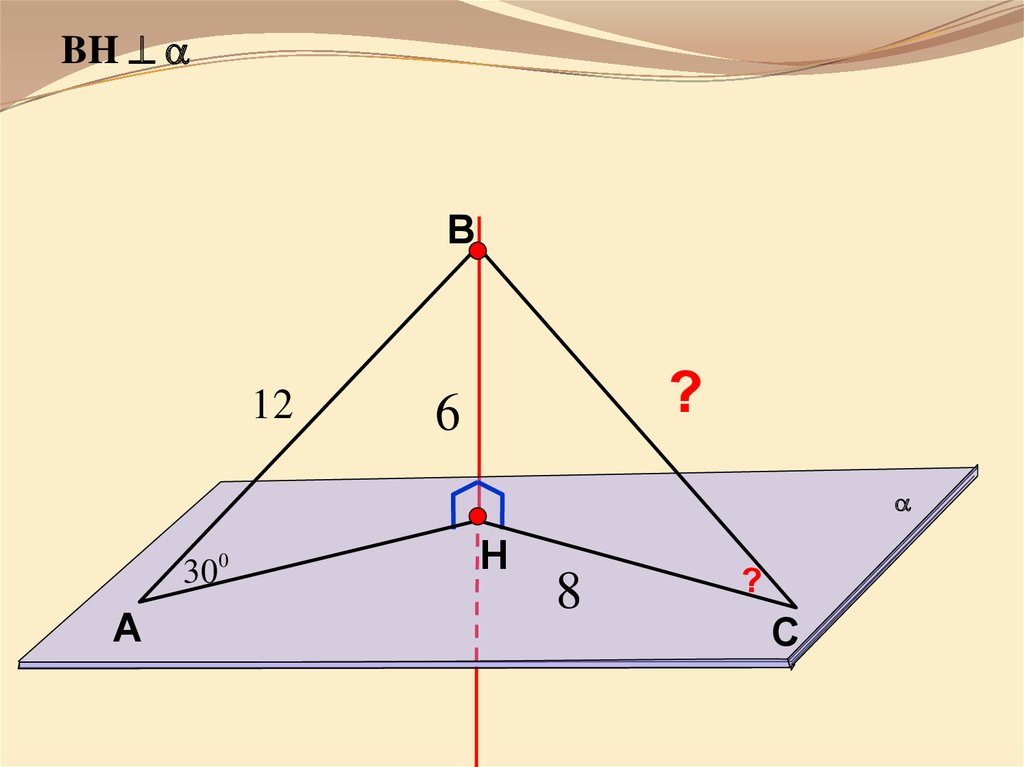
BHВ
12
?
6
30 0
А
H
8
?
С
5.
6.
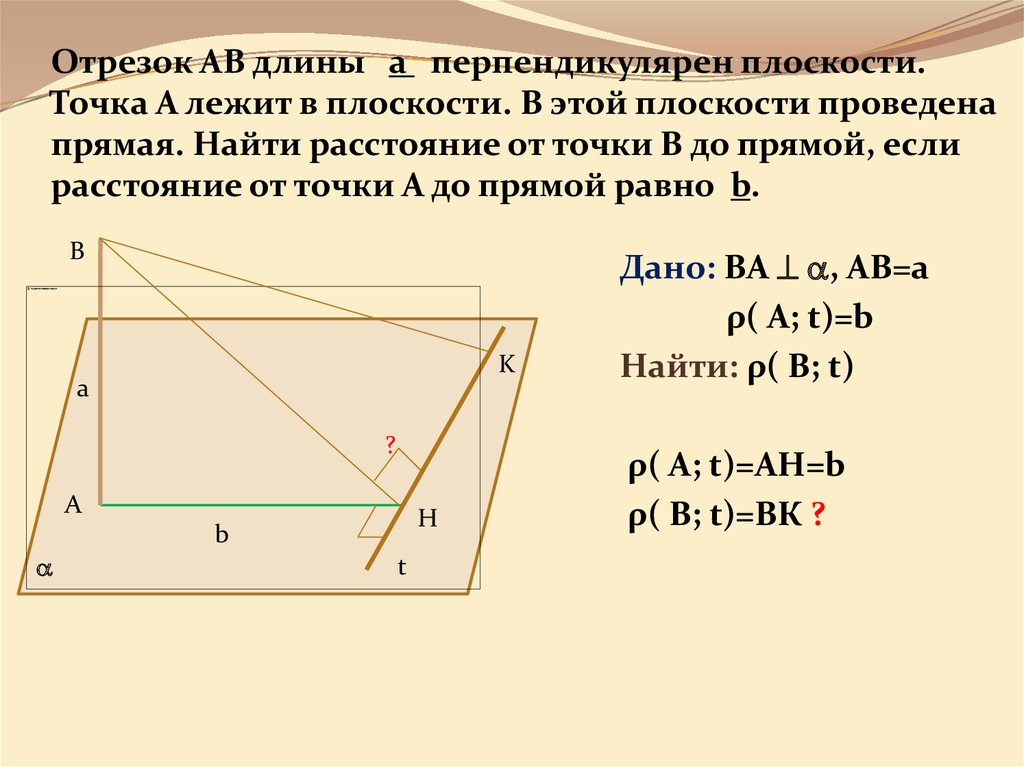
7. Отрезок АВ длины a перпендикулярен плоскости. Точка А лежит в плоскости. В этой плоскости проведена прямая. Найти расстояние от
точки В до прямой, еслирасстояние от точки А до прямой равно b.
В
K
a
?
А
Н
b
t
Дано: ВА , AB=a
ρ( А; t)=b
Найти: ρ( В; t)
ρ( А; t)=AH=b
ρ( В; t)=ВК ?
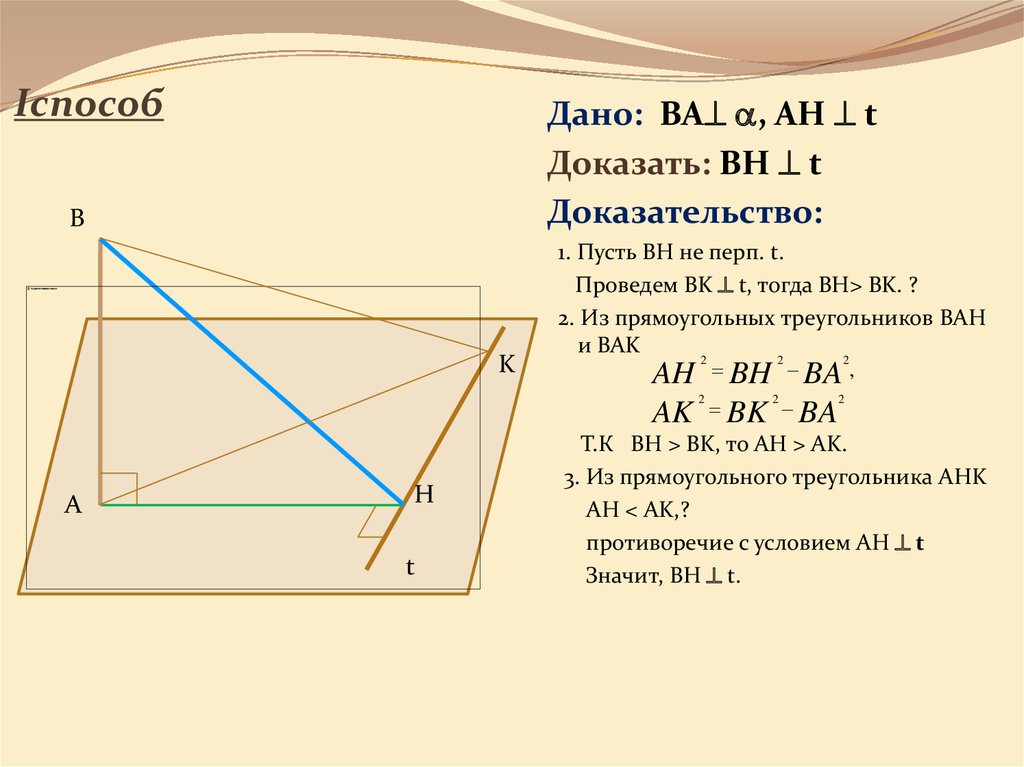
8. Iспособ
Дано: BA , AH tДоказать: BH t
Доказательство:
B
K
1. Пусть BH не перп. t.
Проведем BK t, тогда BH> BK. ?
2. Из прямоугольных треугольников BAH
и BAK
AH BH BA ,
AK BK BA
2
2
A
H
t
2
2
2
2
Т.К BH > BK, то AH > AK.
3. Из прямоугольного треугольника АHK
АH < AK,?
противоречие с условием AH t
Значит, BH t.
9. Теорема о трёх перпендикулярах.
Прямая, проведённая в плоскости через основаниенаклонной перпендикулярно к её проекции на эту
плоскость, перпендикулярна и к самой наклонной
10.
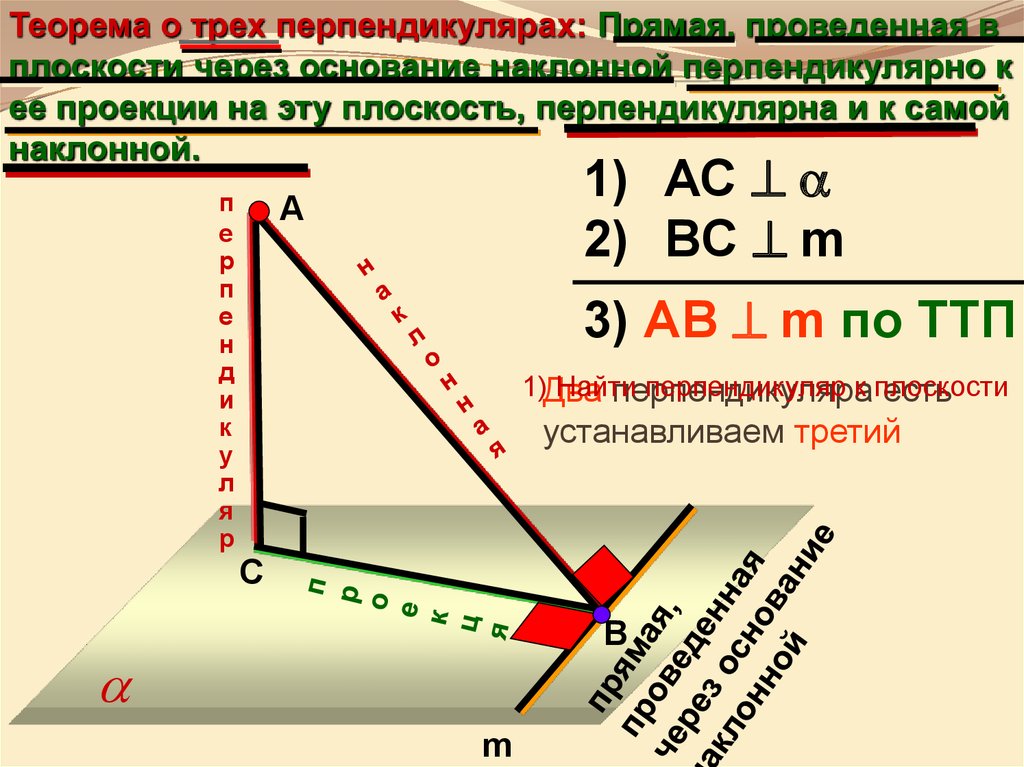
Теорема о трех перпендикулярах: Прямая, проведенная вплоскости через основание наклонной перпендикулярно к
ее проекции на эту плоскость, перпендикулярна и к самой
наклонной.
п
е
р
п
е
н
д
и
к
у
л
я
р
1) АС
2) BС m
А
3) АB m по ТТП
1)Два
Найти
перпендикуляр к плоскости
перпендикуляра
есть
устанавливаем третий
С
В
m
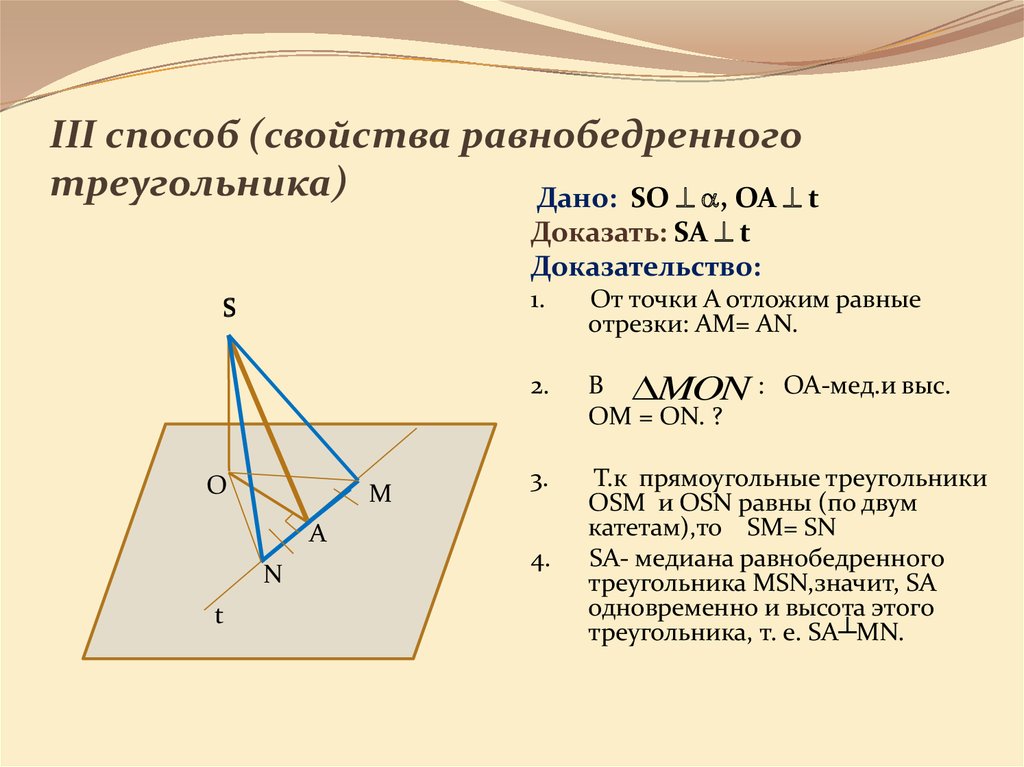
11. III способ (свойства равнобедренного треугольника)
Дано: SO , OA tДоказать: SA t
Доказательство:
S
O
M
A
N
t
1.
От точки А отложим равные
отрезки: АМ= АN.
2.
В MON : ОА-мед.и выс.
ОМ = ОN. ?
3.
Т.к прямоугольные треугольники
OSM и OSN равны (по двум
катетам),то SM= SN
SA- медиана равнобедренного
треугольника MSN,значит, SA
одновременно и высота этого
треугольника, т. е. SA┴MN.
4.
12.
Назовите отрезок, длина которого равна расстояниюот т. М до выделенной прямой. Ответ обоснуйте.
С
п
е
р
п
е
н
д
и
к
у
л
я
р
М
Анализируем дано!
СМ (АВС) по …
СВ АВ по …
Строим МВ!
проекция
В
Делаем вывод!
D
ТТП
А
МВ АВ по ТТП
МВ – искомое расстояние
13. Задача № 1
Дано:М
МВ ( АВС )
В
C
АВСК –прямоугольник.
Доказать:
МСК 90
0
А
К
Задача № 154
14. Задача №154 (Атанасян)
Прямая BD перпендикулярна к плоскоститреугольника АВС. Известно, что BD = 9 см,
АС = 10 см, ВС = ВА = 13 см.
Найдите: а) расстояние от точки D до прямой АС;
б) площадь треугольника ACD.
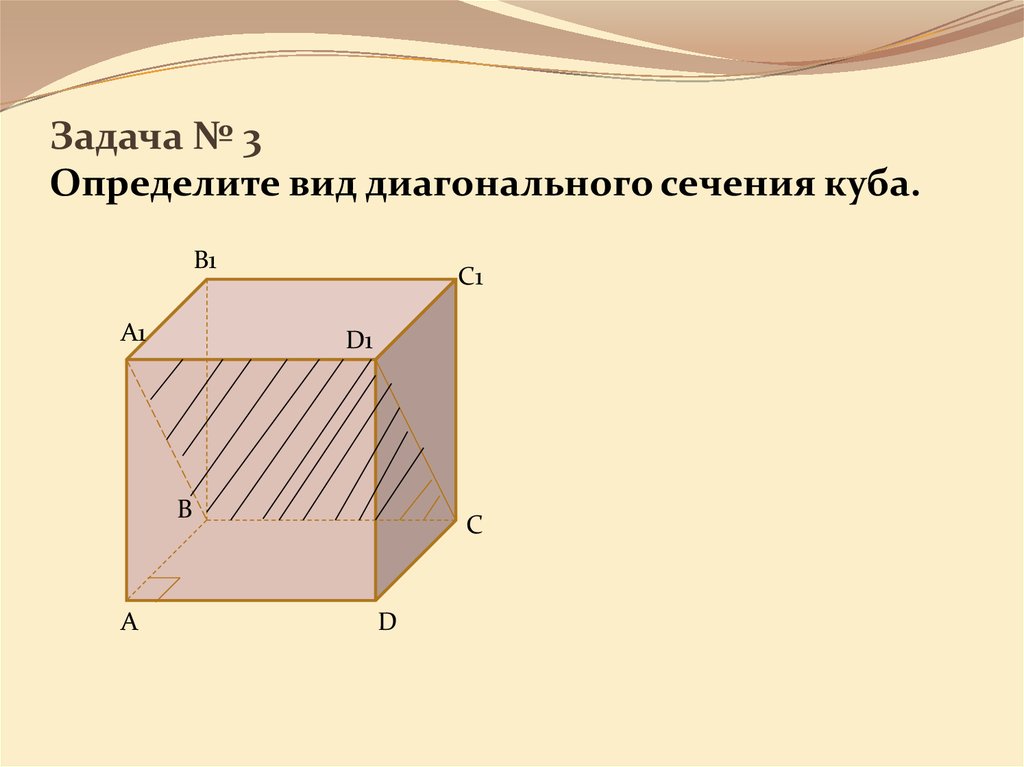
15. Задача № 3 Определите вид диагонального сечения куба.
В1А1
С1
D1
В
А
C
D
16.
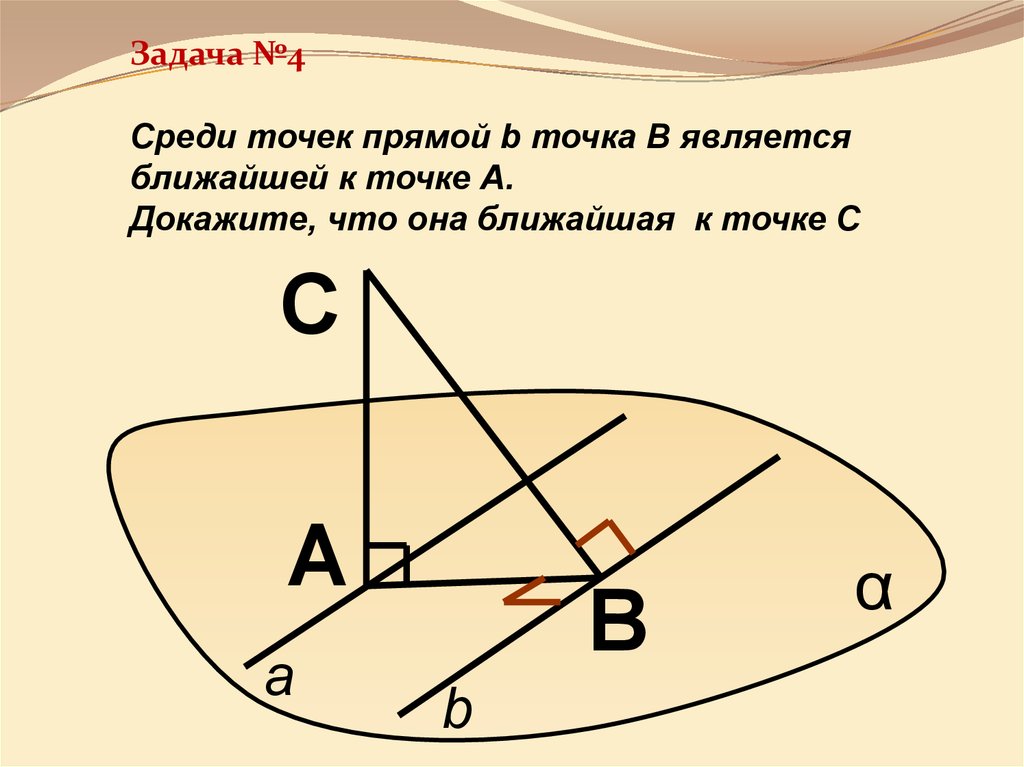
Задача №4Среди точек прямой b точка В является
ближайшей к точке А.
Докажите, что она ближайшая к точке С
C
A
a
B
b
α
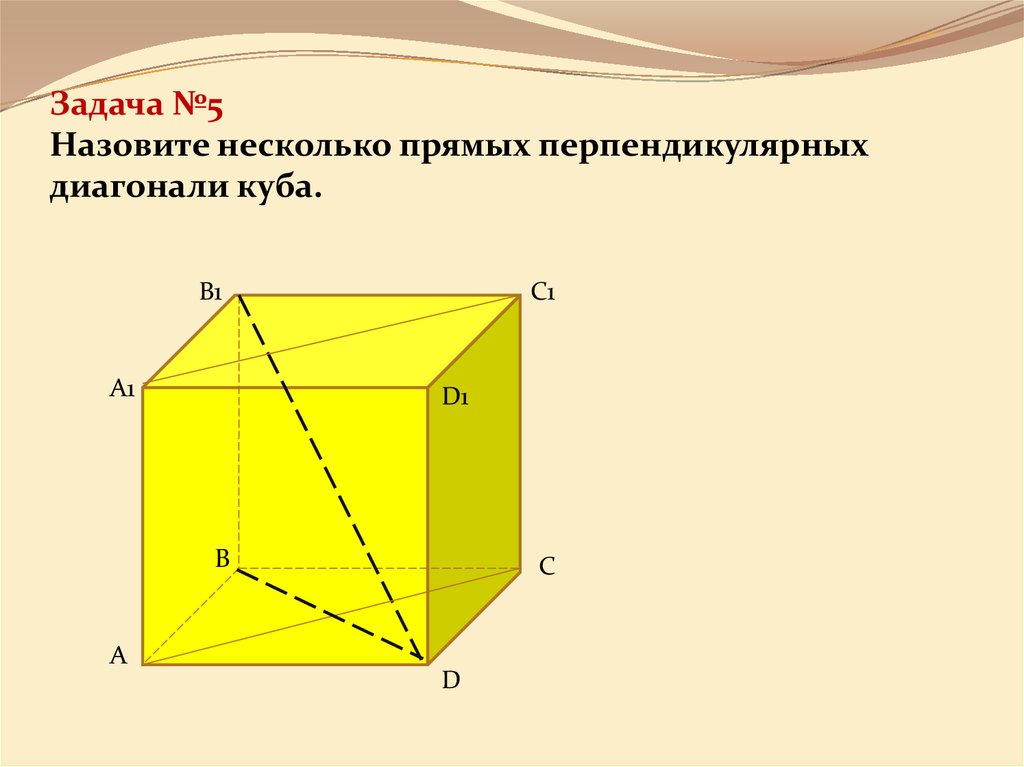
17. Задача №5 Назовите несколько прямых перпендикулярных диагонали куба.
B1А1
C1
D1
В
А
С
D
18. Задача № 6 (145)
DДано:
АВС , С 90 , AD ( ABC )
0
Доказать:
DCB прямоуголь ный.
A
B
19. Подведение итогов.
Дано: AD┴ (АВС),D
ВАС 62 , АСВ 28 .
0
М
A
N
C
B
Каково взаимное
расположение прямых
СВ и BD ?
Ответ обоснуйте.
MN и DB ?
0










 mathematics
mathematics








