Теорема о трех перпендикулярах

1. Теорема о трех перпендикулярах

2. Цель урока:

Изучить теорему «О трех
перпендикулярах».
Научиться применять её при решении
задач.

3. Математический диктант

Задание:
Перечислите и
запишите в
тетради названия
элементов
(отрезков)
чертежа, если АВ
В
С
А

4. Ответ:

АВ – перпендикуляр
ВС
– наклонная
АС
– проекция

5. Дополнительные вопросы:

Какой формулой связанны между
собой перечисленные отрезки?
Чему равно ВС, если АВ = 3 см,
АС = 4 см.?

6. Постановка проблемы

Через конец А отрезка АВ длины b,
проведена плоскость,
перпендикулярная отрезку. И в этой же
плоскости проведена прямая с. Найти
расстояние от точки В до прямой, если
расстояние от точки А до прямой с
равно а.

7. Дан отрезок АВ = в, он перпендикулярен плоскости:

В
в
А

8. В плоскости проводиться прямая, назовем ее СD:

В
D
А
С
По условию задачи известно расстояние от точки А до
прямой СD, оно равно а.

9. Расстояние от точки до прямой, есть перпендикуляр, проведенный из этой точки на прямую!

D
А
C

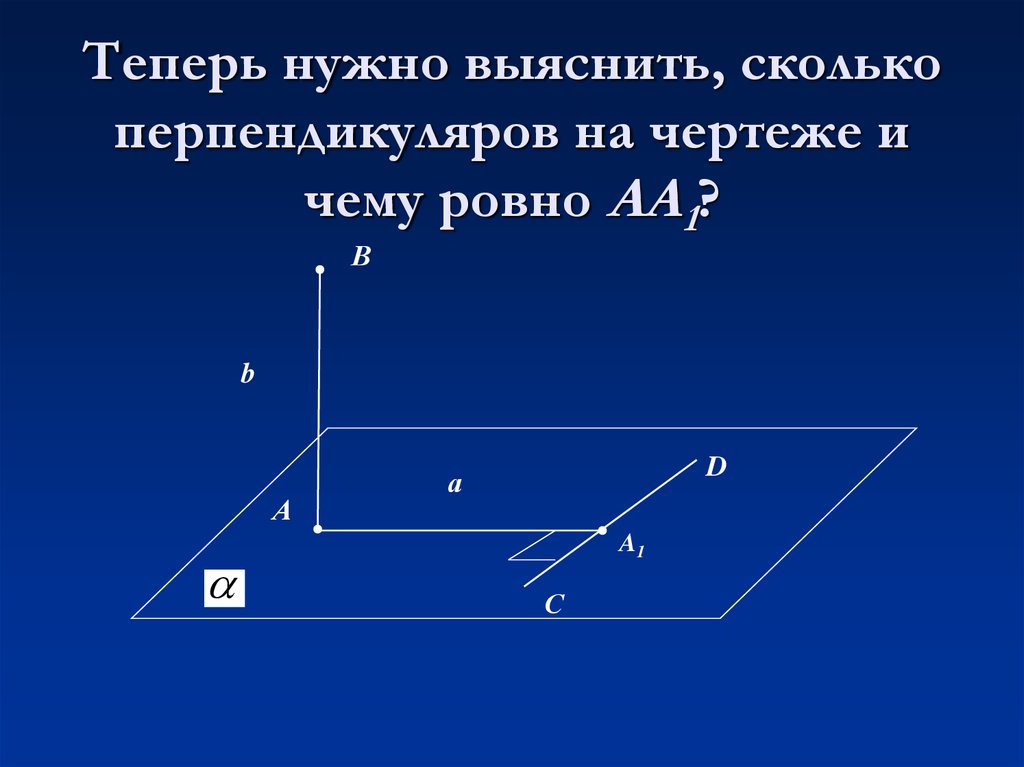
10. Теперь нужно выяснить, сколько перпендикуляров на чертеже и чему ровно АА1?

В
b
А
D
а
A1
С

11. Куда пойдет перпендикуляр из точки В? Где будет находиться его основание на прямой CD?

В
D
А
А1
С

12. Первый выступающий

13.

А1
А
с
Дано: ;
с
,АС – наклонная,
ВС – проекция. ВС с , АВ .
В
С
Доказать: АС с

14. Второй выступающий

15.

А
Дано:
с
;
АС – наклонная, ВС –
с , АВ .
Доказать: АС с .
проекция. ВС
с
В
С
D

16. Третий выступающий

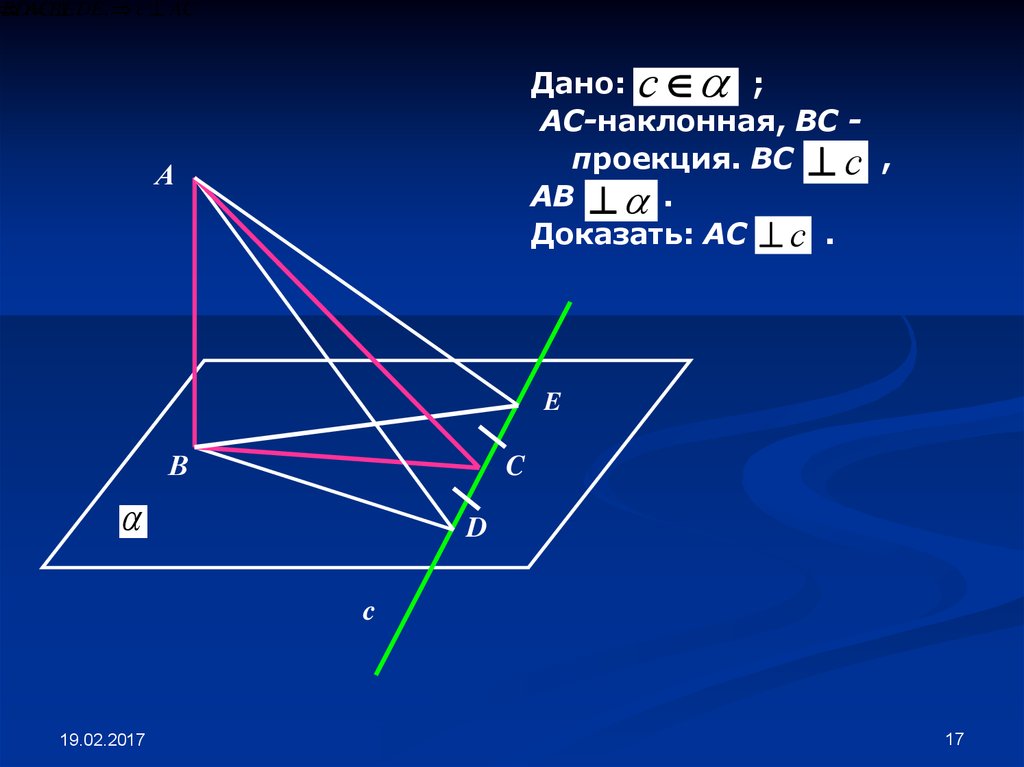
17.

DE, c AC
BDAC
BE
Дано: с
;
АС-наклонная, ВС проекция. ВС с ,
АВ .
Доказать: АС с .
А
E
В
C
D
c
19.02.2017
17

18. Продолжим решение предложенной в начале урока задачи

19.

АВ , А , АВ в
В
Дано:
D
,
AA1 CD , AA1 a
в
А
АВ , АВ в
А1
а
С
Найти: Расстояние от точки
В до прямой CD
Решение.
1) Расстояние от точки до
прямой является перпендикуляр
По теореме «О трех перпендикулярах».
BA1 CD , т.к. AA1 - проекция наклонной ВА1.
A1 B 2 AB 2 AA1 ,
2
0
ABA
(
A
90
) ,По теореме Пифагора:
1
Из
A1 B
Ответ: Расстояние от точки В до прямой CD равно
19.02.2017
AB 2 AA1
а2 в2
19
2

20. Практическое применение теоремы о трех перпендикулярах

21. Задача:

В правильной треугольной пирамиде
боковые грани наклонены под углом .
D
А
О
С
К
19.02.2017
В
21

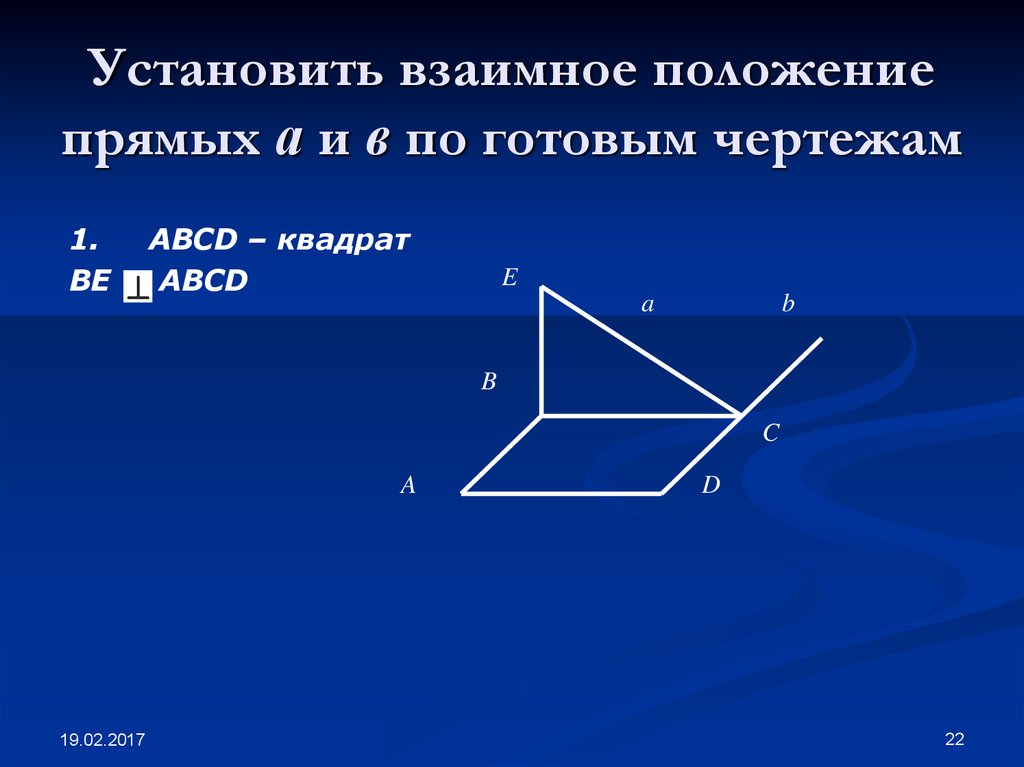
22. Установить взаимное положение прямых а и в по готовым чертежам

1.
ABCD – квадрат
BE ABCD
E
a
b
B
C
A
19.02.2017
D
22

23. Установить взаимное положение прямых а и в по готовым чертежам

2. ABCD – квадрат
BE ABCD
E
a
b
B
C
A
19.02.2017
D
23

24. Установить взаимное положение прямых а и в по готовым чертежам

3.
ABCD – ромб
AE
E
ABCD
b
a
B
А
O
D
19.02.2017
C
24

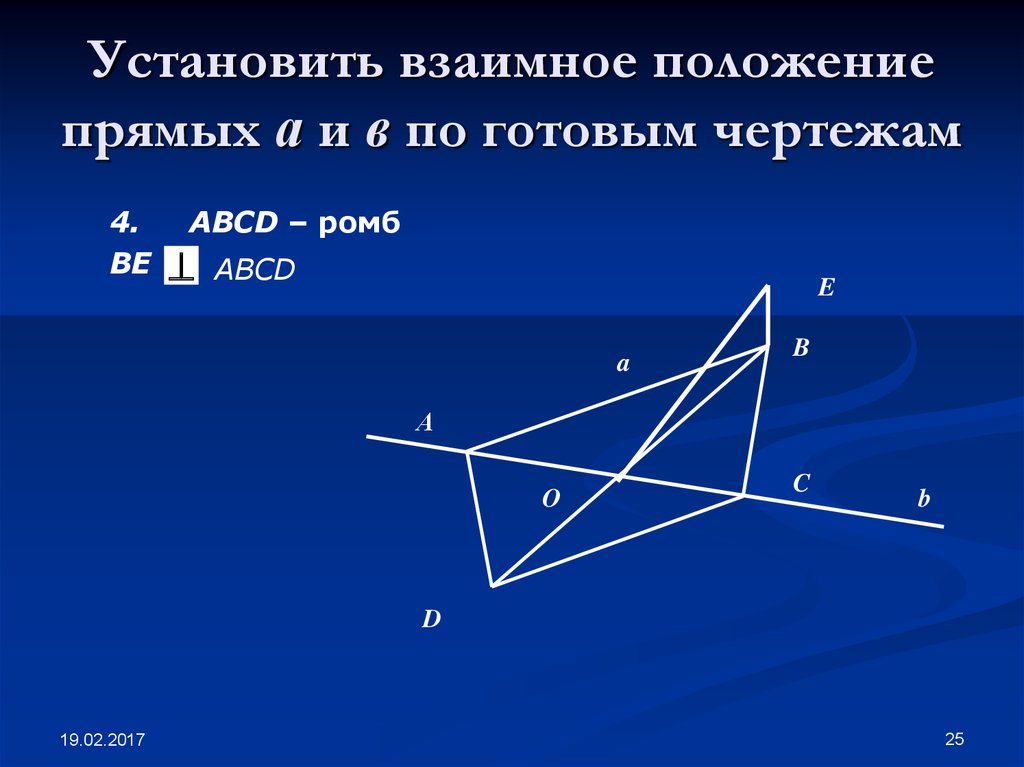
25. Установить взаимное положение прямых а и в по готовым чертежам

4.
BE
ABCD – ромб
ABCD
E
a
B
А
O
C
b
D
19.02.2017
25

26. Самостоятельная работа

На оценку 3: Решить 3 задачи из уровня А
На оценку 4: Решить по одной задачи из
уровня А и В (на выбор любые).
На оценку 5: Решить по одной задачи из
уровня А, В и С ( на выбор любые).
19.02.2017
26

27. Подведение итогов урока.