Similar presentations:
Графики квадратичной функции и обратной пропорциональности
1. Функция y = x2 и её график
Функция y =и её график
2
x
2.
Расшифруйте терминыФункция
Область
определения
Аргумент
Функция,
заданная
формулой
вида y независимая
= плоскости,
kx +при
b, где
Множество
Зависимость
Все значения,
всех
между
которые
точек
двумя
координатной
принимает
переменными,
которой
Независимая переменная, значения которой
абсциссы
хкаждому
переменная.
– переменная,
которых
значению
k иравны
bнезависимой
некоторые
значениям
числа,
переменной
аргумента,
её графиком
а
выбирают произвольно.
ординаты
соответствует
является
прямая.
– соответствующим
единственное значение
значениям
зависимой
функции.
переменной.
График функции
Линейная функция
3. Зависимость площади квадрата от длины его стороны
S aЗависимая
переменная
а
а
2
Независимая
переменная
2
y
y = xx
квадратичная функция
4.
Математическоеисследование
Функция y =
2
x
5.
Заполните таблицу значений функции y = x2:х
y
х
y
- 3 - 2,5
- 2 - 1,5
- 1 - 0,5
- 9 - 6,25 - 4 - 2,25 - 1 - 0,25
0
0
0
0,5
1
1,5
2
2,5
3
0
2,5
1
2,5
4
6,25
9
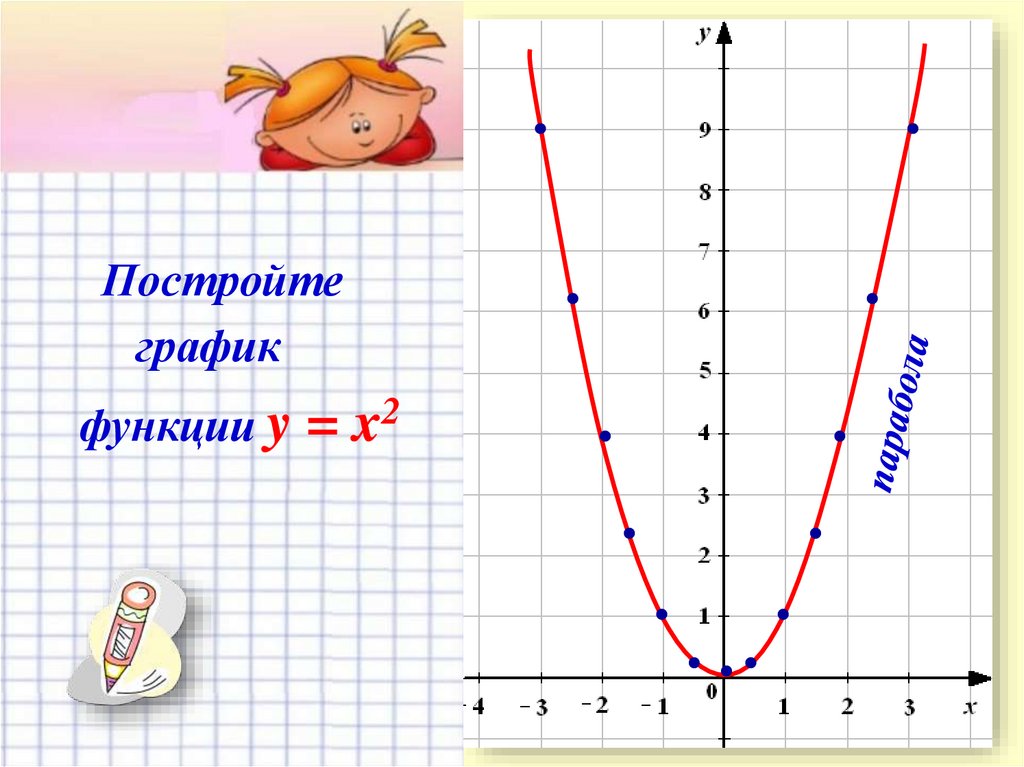
6.
Постройтеграфик
функции y
= x2
7. Многоликая парабола
8.
Древнегреческий математикИсторическая
справка
Аполлоний Пергский
( Перге, 262 до н.э. — 190 до н.э.)
разрезав конус, линию среза назвал
параболой, что в переводе с греческого
означает «приложение» или «притча»,
о чём математик и написал в
восьмитомнике «Конические сечения».
И долгое время параболой называли
лишь линию среза конуса, пока не
появилась квадратичная функция.
9.
Знаете ли вы?Траектория камня,
брошенного под углом к
горизонту
10.
11.
Невероятно,но факт!
Перевал Парабола
12.
Функцияk
у
x
,
её свойства и график.
13.
y=k
x
- обратная
пропорциональность,
где k ≠ 0 – заданное число.
Графиком является гипербола
14.
Построим график функции:1
1
х
1 2 4 6
4
2
1
1
1
у
1
4 2
2
4
6
у
Гипербола
4
в I и III
Гипербола
3
координатных
симметрична
2
четвертях.
относительно
начала
-6
-4 -3 -2 -1 1
1
у
x
х 0
II
координат.
- - - - - - - - - - -
I
6х
0 -1 1 2 3 4
Ось х и ось у –
асимптоты
гиперболы.
-2
-3
-4
III
IV
15.
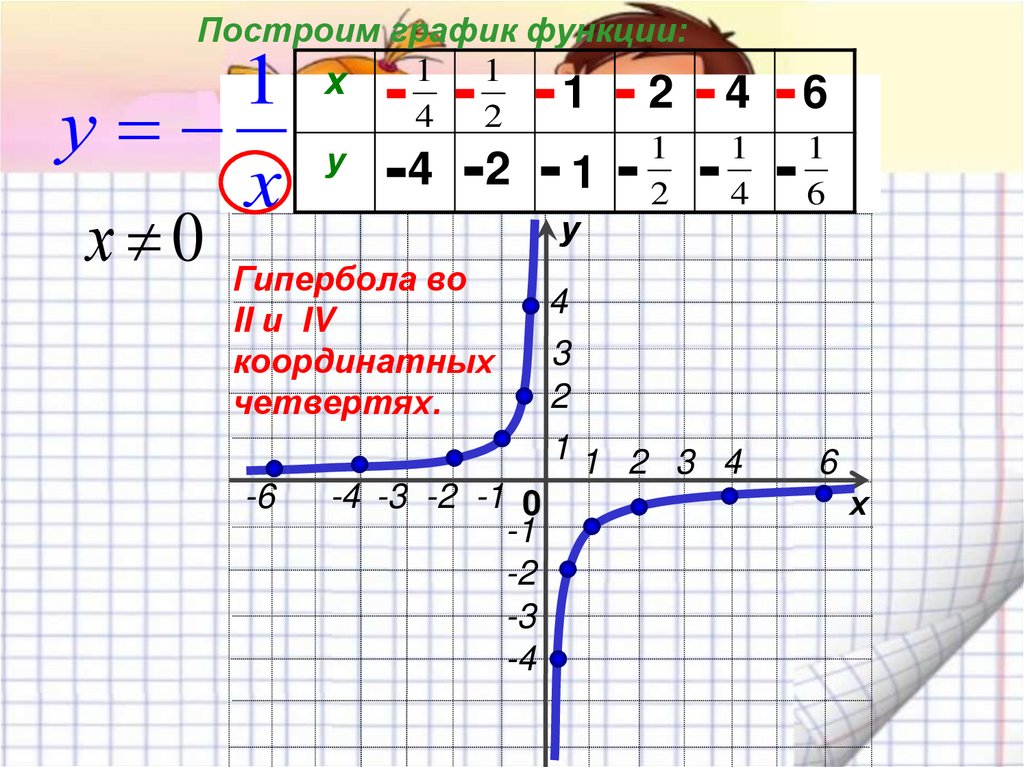
Построим график функции:1
1
х
1 2 4
4
2
1
1
у
4 2 1 2 4
у
Гипербола во
4
II и IV
3
координатных
2
четвертях.
11 2 3 4
-6
-4 -3 -2 -1 0
-1
-2
-3
-4
1
у
x
х 0
- - - - - -6
1
- - - - - -6
6
х














 mathematics
mathematics