Similar presentations:
Равновесные и неравновесные носители зарядов
1. Твердотельная электроника
Электронный учебно-методическийкомплекс
Твердотельная электроника
Презентации к лекционному курсу
Равновесные и неравновесные носители зарядов
МОСКВА
2016
НИУ «МЭИ»
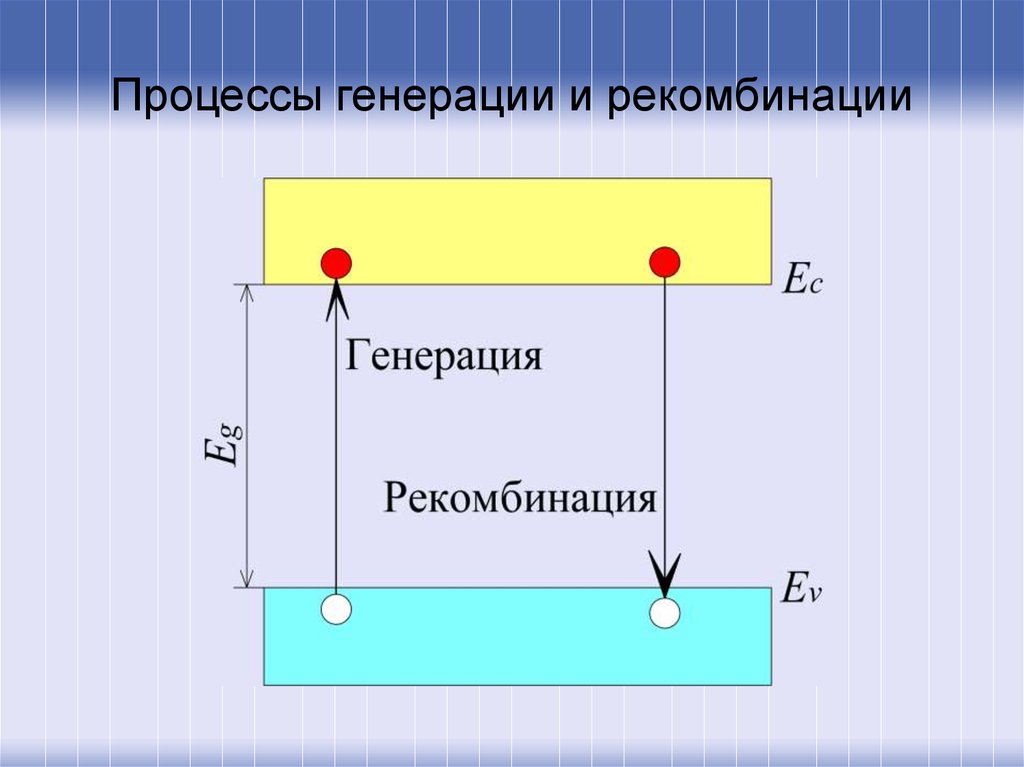
2. Процессы генерации и рекомбинации
3.
Под равновесными носителями заряда понимаютсвободные электроны и дырки, возникшие в результате
тепловой генерации и находящиеся в тепловом равновесии с
решеткой кристалла. Равновесная концентрация электронов n0
и дырок p0 характеризуются положением уровня Ферми.
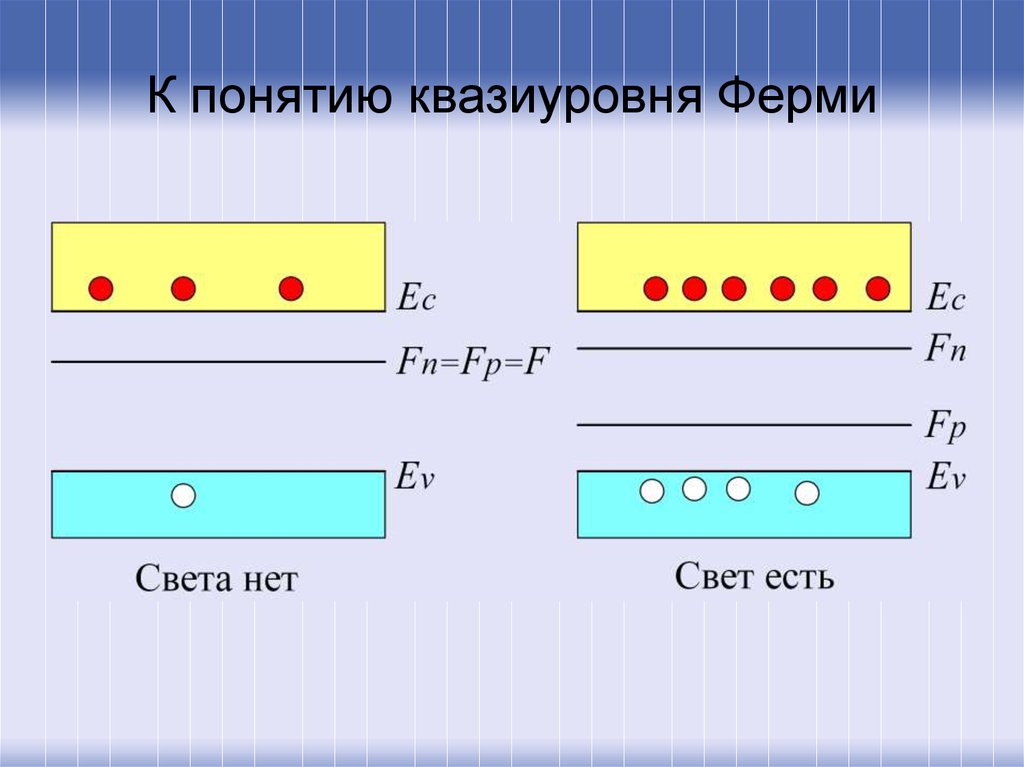
В отличие от равновесных, у избыточных неравновесных
носителей заряда, появляющихся в результате освещения с
энергией квантов h E g или инжекции (их концентрации
2
обозначаются как Δn и Δp) условие n p ni не соблюдается, и
концентрации
неравновесных
носителей
заряда
характеризуются квазиуровнями Ферми для электронов Fn и
для дырок Fp.
4. Расчет концентрации избыточных носителей заряда
5. К понятию квазиуровня Ферми
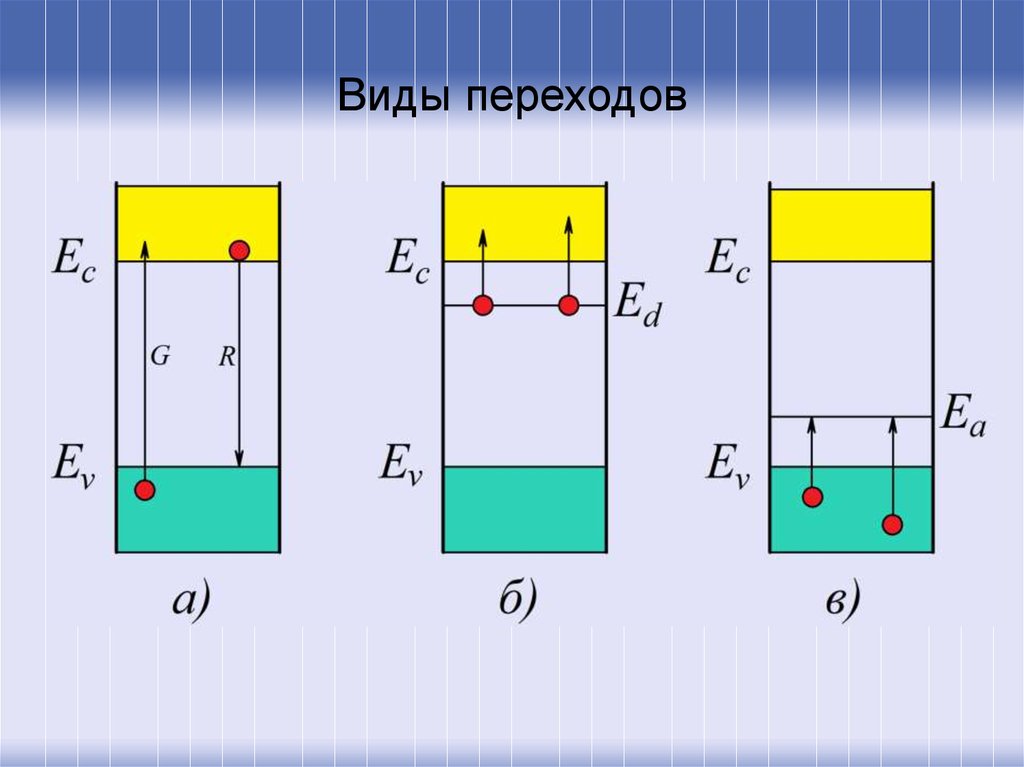
6. Виды переходов
7.
В равновесном состоянии скорость генерации (числоэлектронов, генерируемых в единице объема в единицу
времени) равна скорости рекомбинации (число электронов,
рекомбинирующих в единице объема в единицу времени):
G0 R0 n0 p0
где γ – коэффициент
коэффициент рекомбинации.
пропорциональности
или
8.
Концентрация неравновесных носителей может бытьменьше концентрации равновесных носителей ( n n0
,
. p p0 ), в этом случае говорят о низком уровне возбуждения
или низком уровне инжекции.
При высоком уровне возбуждения или высоком уровне
инжекции концентрация неравновесных носителей сравнима
или превышает равновесную концентрацию.
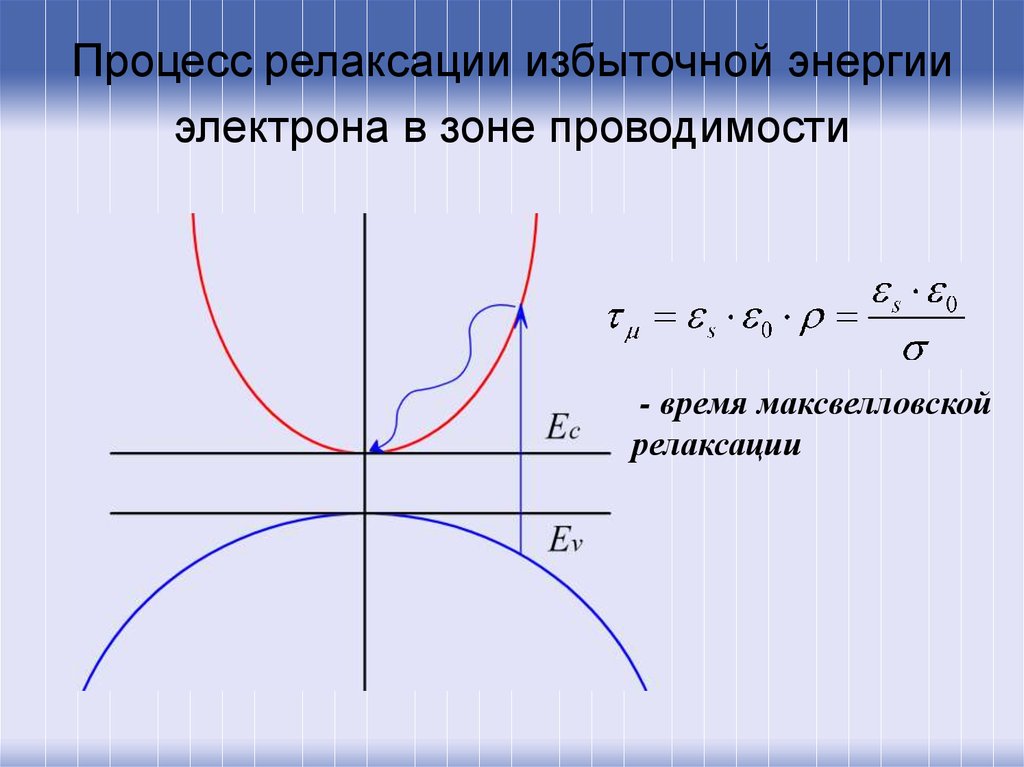
9. Процесс релаксации избыточной энергии электрона в зоне проводимости
- время максвелловскойрелаксации
10.
Появление неравновесных носителей заряда приводит кувеличению проводимости
σ q (μ n n0 μ p p0 μ n Δn μ p Δp )
Δσ q (μn Δn μ p Δp )
Скорость,
с
которой
протекает
рекомбинация,
определяется временем жизни неравновесных носителей
заряда .
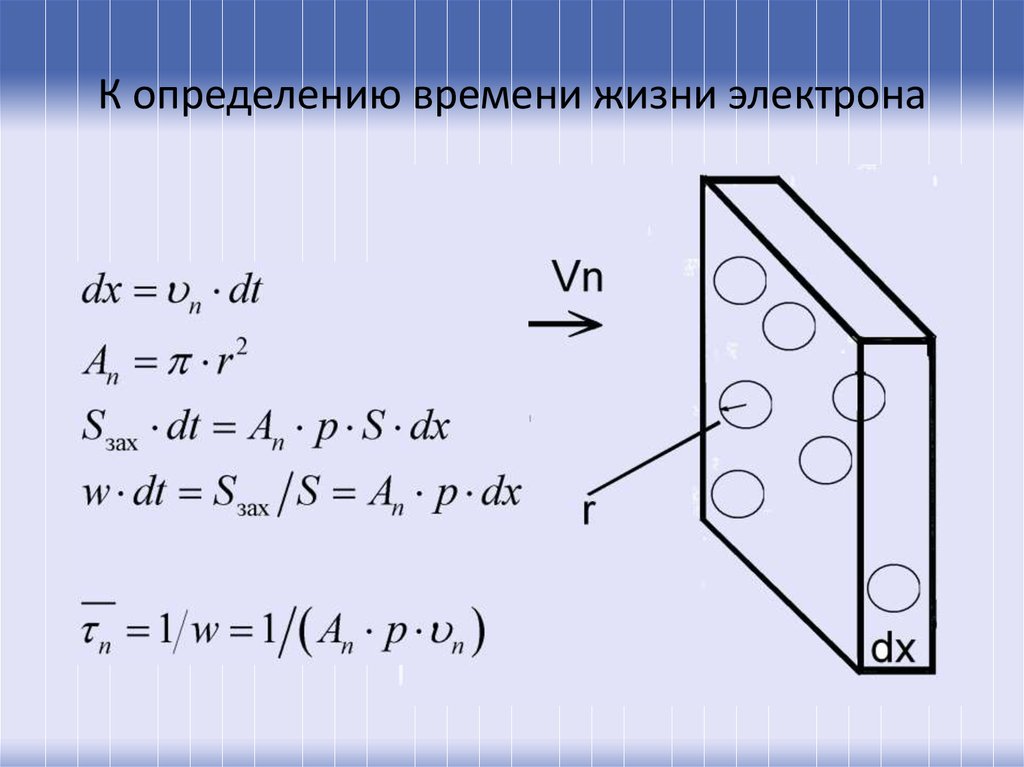
11. К определению времени жизни электрона
12. Расчет скорости рекомбинации
13.
Изменение концентрации носителей во времени всостоянии термодинамического равновесия определяется
уравнением непрерывности:
n p
G R 0
t t
где G – скорость генерации, R – скорость рекомбинации
14. Возбуждение носителей заряда в собственном полупроводнике
15.
Послеснятия
возбуждения
(выключения
света,
прекращении инжекции) (G=0) концентрации электронов и
дырок уменьшаются в результате рекомбинации, и кристалл
возвращается к равновесному состоянию, в котором Δn=0 и
Δp=0.
Скорость рекомбинационных процессов (исчезновение
избыточных
носителей,
после
снятия возбуждения)
характеризуется их временем жизни неравновесных
носителей заряда n , p . При рекомбинации зона-зона
n = p . При G=0 уравнение непрерывности примет
вид:
n
n n0
n
t
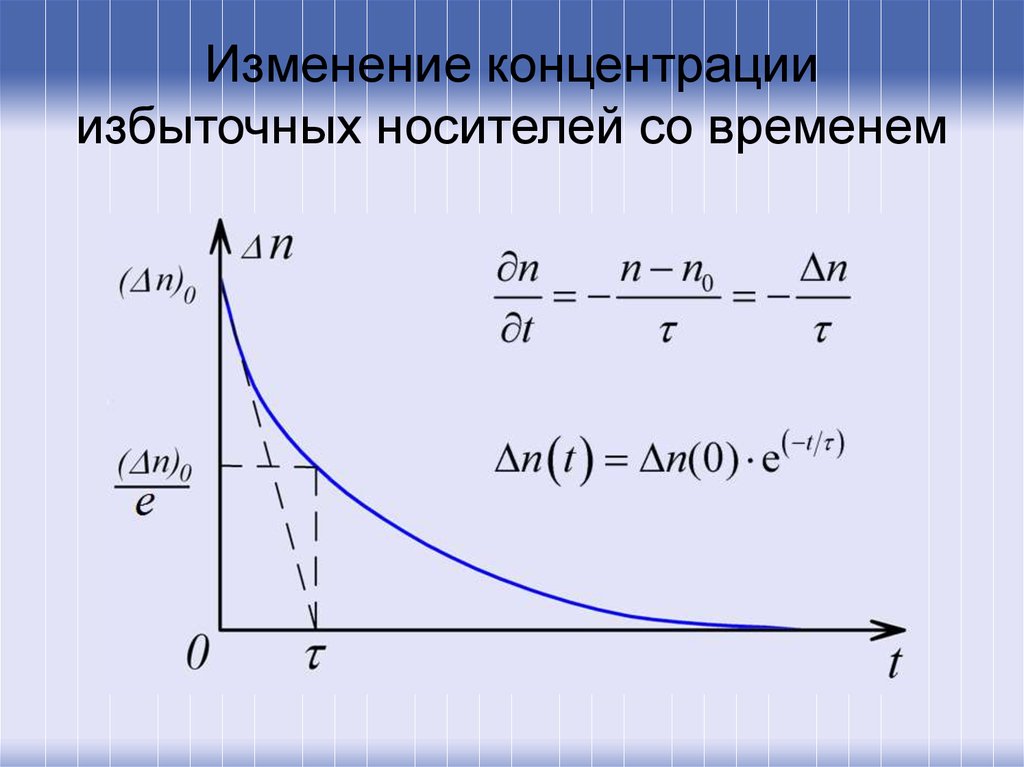
16. Изменение концентрации избыточных носителей со временем
17.
Линейная рекомбинация характерна при низком уровнеинжекции носителей, при высоком уровне возбуждения
процессы определяются квадратичной рекомбинацией:
n
n p n 2
t
18.
Отметим, что преобладание того или иного процесса(генерации или рекомбинации носителей) зависит от
соотношения между концентрациями равновесных и
неравновесных носителей: если np n0 p0 преобладает процесс
рекомбинации (например, при прямом смещении pnперехода), если np n0 p0
преобладает процесс генерации
носителей (например, при обратном смещении pn-перехода, в
режиме отсечки биполярного транзистора).
19.
Малый уровень возбужденияn n0 p0
тогда:
n p
n p n0 p0 n0 n p0 p n0 p0
t t
n0 p0 n0 p n p0 n p n0 p0 n0 p n p0
С учетом того, что n p
n p
n n0 p0
t t
20.
Введем обозначение:1
n0 p0
,
Тогда выражение примет вид:
n n0
n
n
t
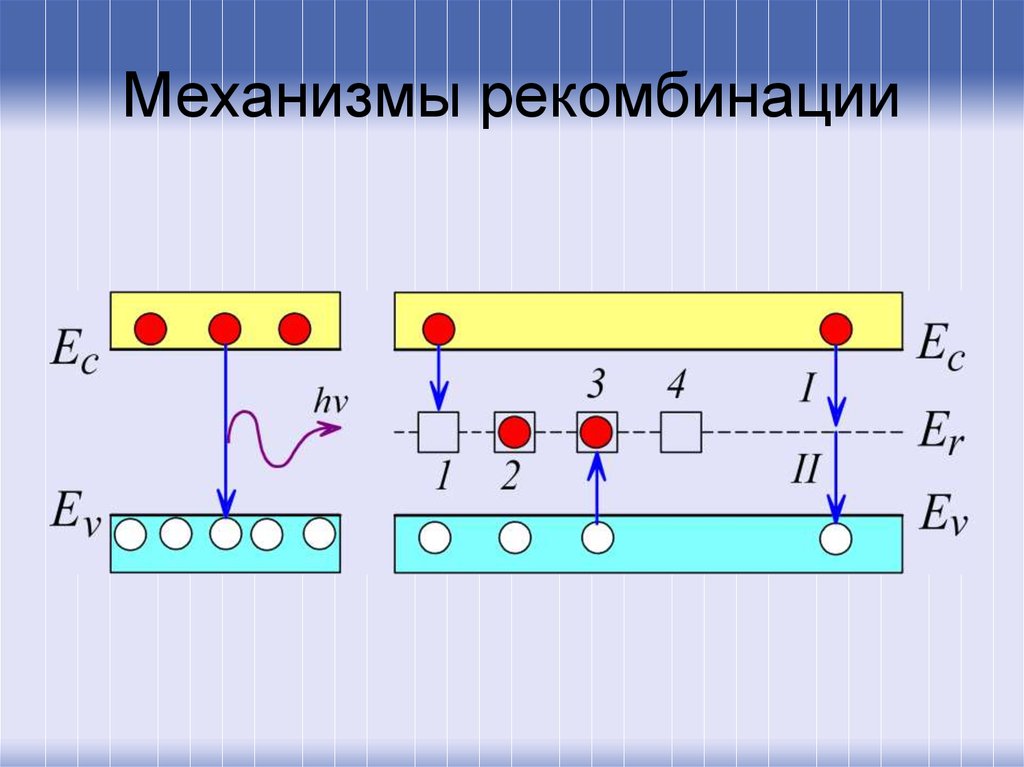
21. Механизмы рекомбинации
• прямая межзонная• через локальные уровни (ловушки, центры
рекомбинации)
• поверхностная.
22. Механизмы рекомбинации
23. Межзонная рекомбинация
• Излучательная,поскольку
энергия,
выделяемая
при
E h каждой
Ec Ev E g
рекомбинации
пары
излучается в виде фотона с
энергией
.
Скорость
R излучательной
n p
рекомбинации
пропорциональна
произведению концентраций
электронов и дырок:
.
• Безызлучательная или фононная; ударная или Ожерекомбинация (ΔЕ передается третьему носителю заряда,
24.
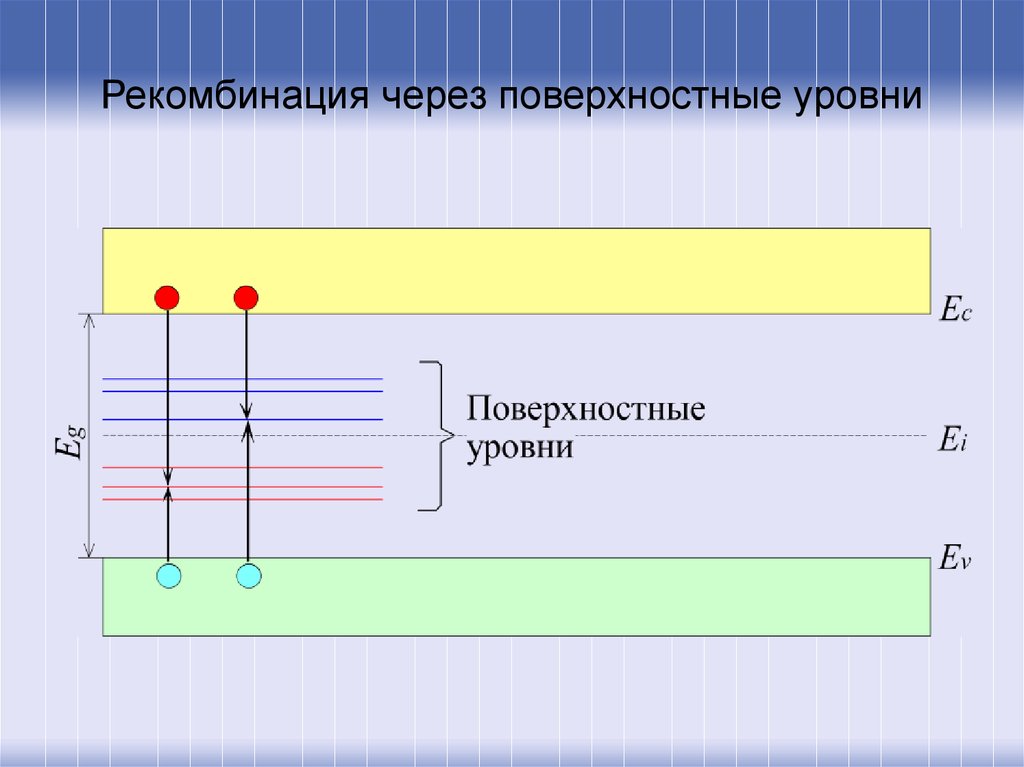
Вероятность межзонной рекомбинации очень мала, болеевероятны переходы носителей заряда через локальные уровни,
расположенные в запрещенной зоне, т.е. ловушечная
рекомбинация или рекомбинация Шокли-Рида
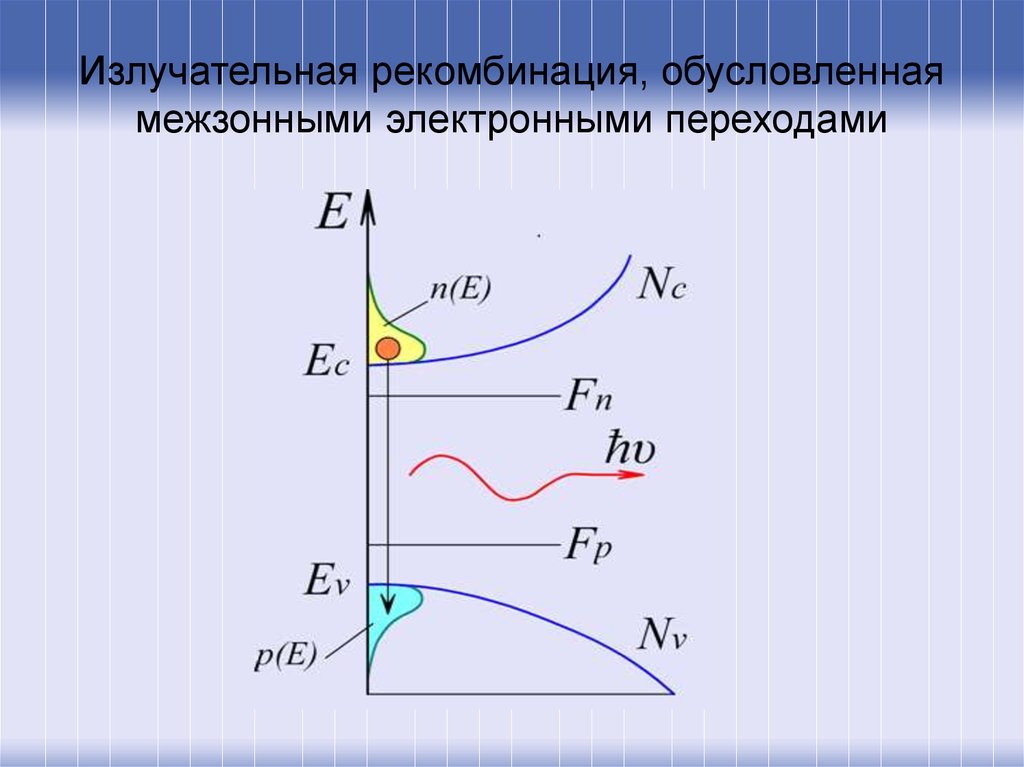
25. Излучательная рекомбинация, обусловленная межзонными электронными переходами
26. Рекомбинация через поверхностные уровни
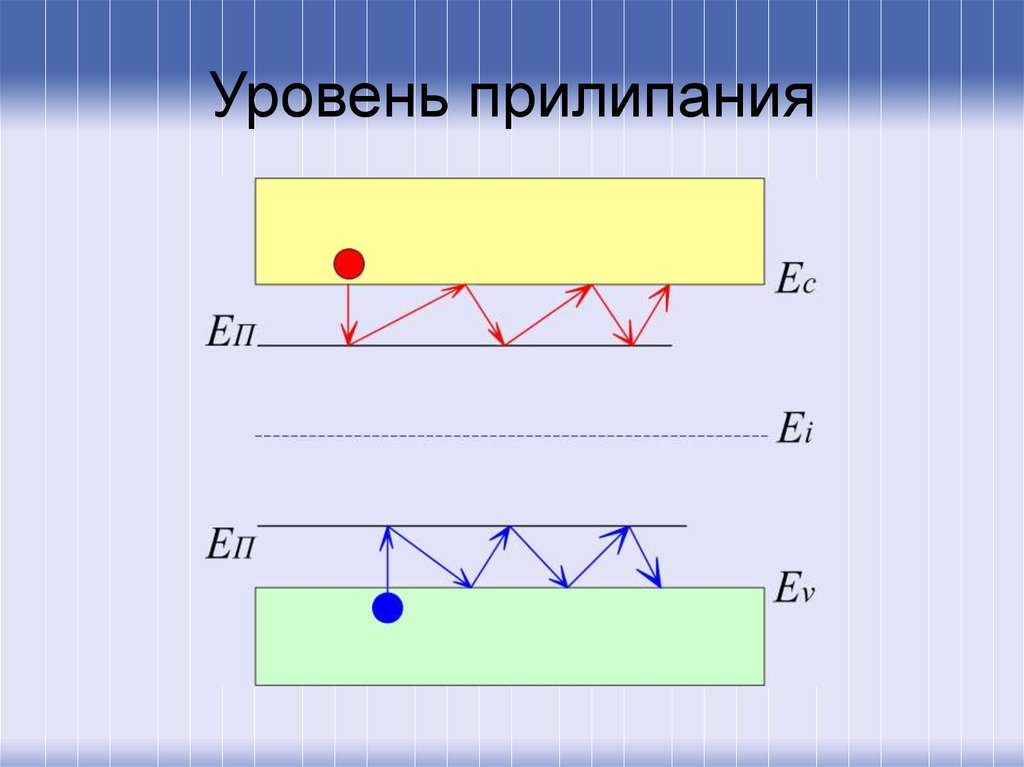
27. Уровень прилипания
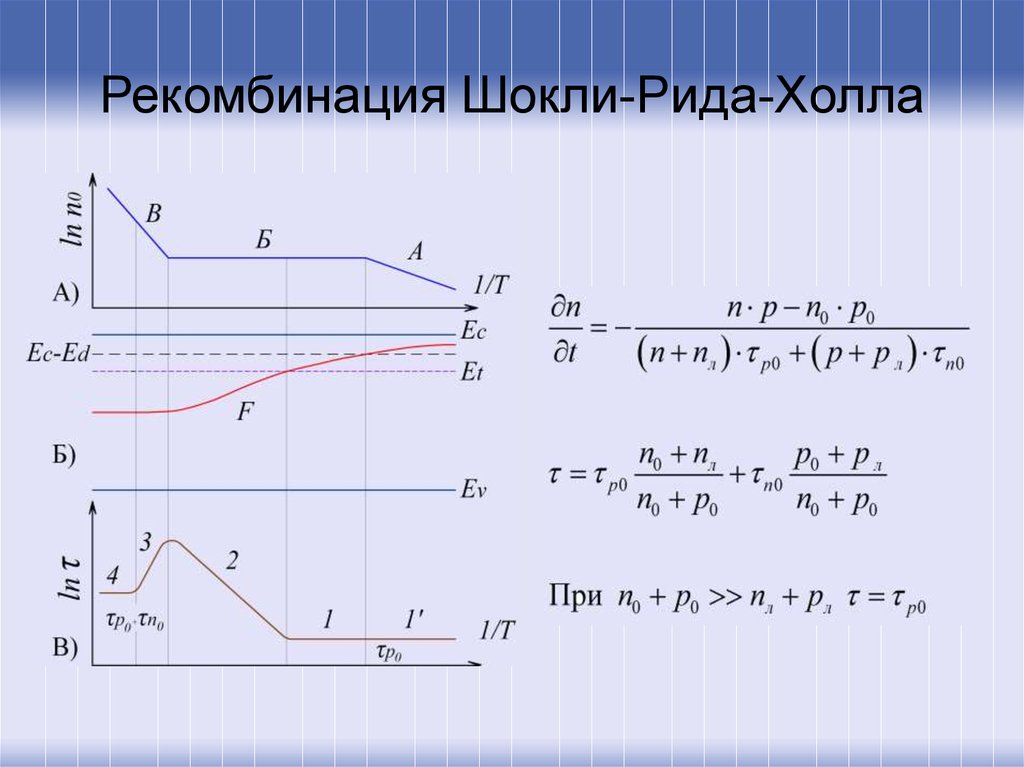
28. Рекомбинация Шокли-Рида-Холла
29.
n0– для полупроводника p-типа;
p0
– для полупроводника n-типа.
>>
Время жизни неравновесных
носителей заряда
связано с временами их жизни в объеме V и у поверхности
s следующим соотношением:
1
1
V
1
S
Обычно на практике V S
30.
Наличие у поверхности полупроводника уровня Es,выполняющего роль «стока» для неравновесных носителей
заряда, приводит к возникновению направленных потоков
носителей к поверхности, пропорциональных значениям их
избыточной концентрации:
jn
Sn n
q
sn , s p
jp
q
S p p
выражают относительную долю избыточных
носителей заряда, ежесекундно рекомбинирующих в единице
площади поверхности полупроводника, эти коэффициенты
имеют размерность скорости и называются скоростями
поверхностной рекомбинации электронов и дырок.
31.
Для идеальной поверхности, эквивалентной любойвоображаемой поверхности в объеме полупроводника, S 0
Для поверхности идеального металлического
контакта S
Бесконечное
значение
скорости
поверхностной
рекомбинации означает, что на поверхности полупроводника
всегда ns p s 0 ,т.е.
поверхностные
концентрации
электронов и дырок всегда остаются равновесными
( p s p 0 n s n0 ). Такие идеальные контакты называются
омическими.
В моделях приборов скорость
рекомбинации обычно полагают бесконечной
поверхностной
32.
• Эдвин ГербертХолл (Edwin
Herbert Hall)
американский
физик
• 7.11.185520.11.1938
33. Эффект Холла
• Исследования эффекта Холла позволяютопределить основные электрофизические
свойства полупроводников
• Кинетические эффекты, возникающие при
одновременном воздействии на проводник
электрического и магнитного полей,
называют гальваномагнитными
эффектами. Эффект Холла является одним
из таких эффектов
34.
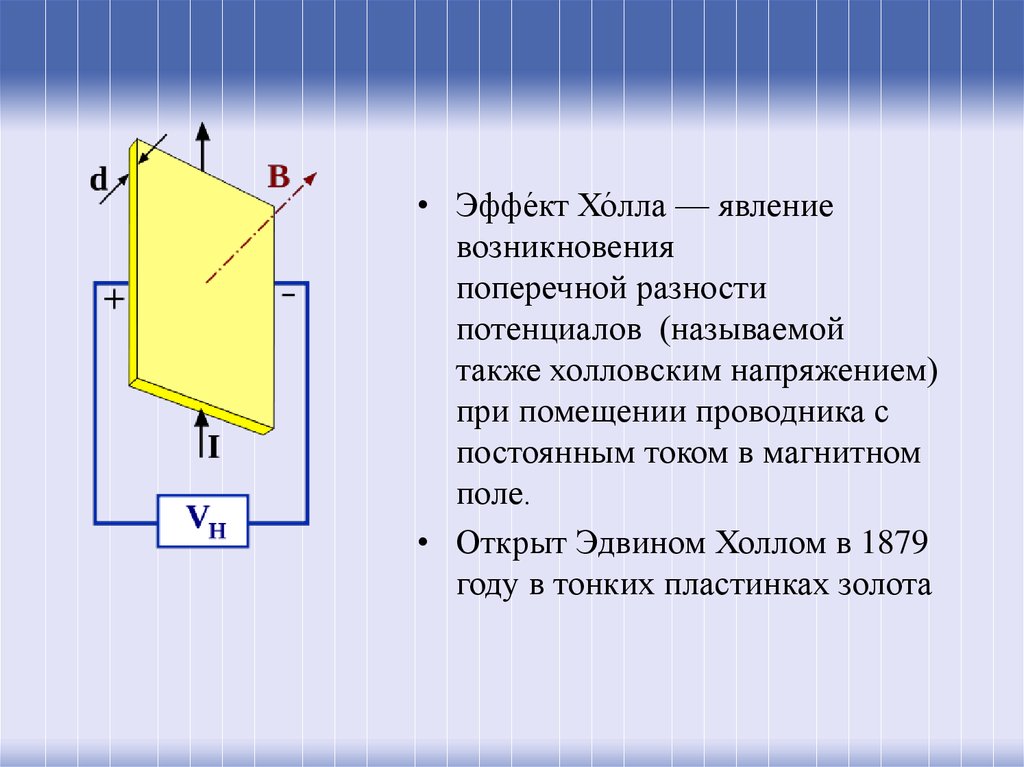
• Эффе́кт Хо́лла — явлениевозникновения
поперечной разности
потенциалов (называемой
также холловским напряжением)
при помещении проводника с
постоянным током в магнитном
поле.
• Открыт Эдвином Холлом в 1879
году в тонких пластинках золота
35. Классический эффект Холла
• Уравнение стационарного движенияносителей заряда в электрическом поле
ямы
, параллельном плоскости квантовой
B
XY, и магнитном поле
, параллельном
оси Z, описывается уравнением,
вытекающим из равенства по величине сил
трения и Лоренца:
d
m *
m*
q F B
0
dt
36.
• С практической точки зрения обычно представляютинтерес эффект Холла в слабом и сильном магнитном
поле.
• Известно, что в однородном магнитном поле заряженная
частица должна двигаться по круговой траектории
радиуса r, ось которой параллельна вектору
• Однако, если длина свободного пробега электрона (или
дырки) много меньше r, то поле B "не успевает" на длине
значительно "закрутить" электрон. Такое поле называется
слабым.
37.
• Частота вращения электрона под действием магнитногополя с индукцией (частота циклотронного резонанса) в
плоскости, перпендикулярной Вz,, равна:
qB m* 2 Tc
• где Тс период обращения по круговой орбите. Магнитное
поле считается малым, если выполняется условие τ/Тс<<1
т.е. период обращения носителя заряда по круговой
орбите много больше времени релаксации τ.
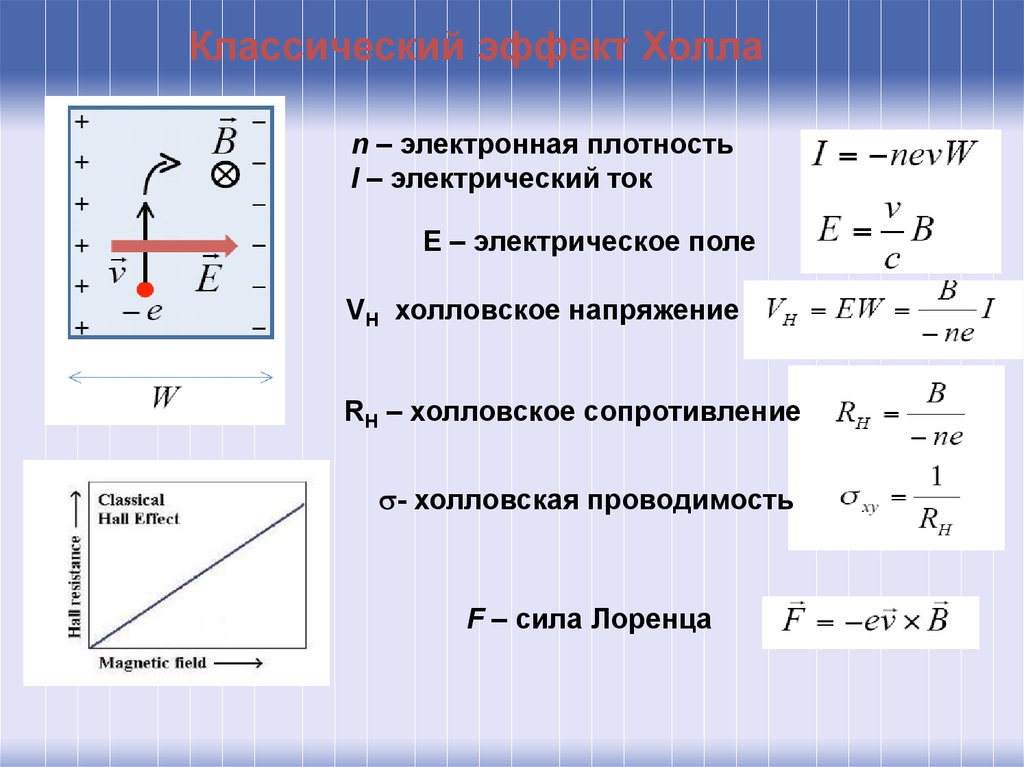
38.
Классический эффект Холлаn – электронная плотность
I – электрический ток
E – электрическое поле
VH холловское напряжение
RH – холловское сопротивление
- холловская проводимость
F – сила Лоренца
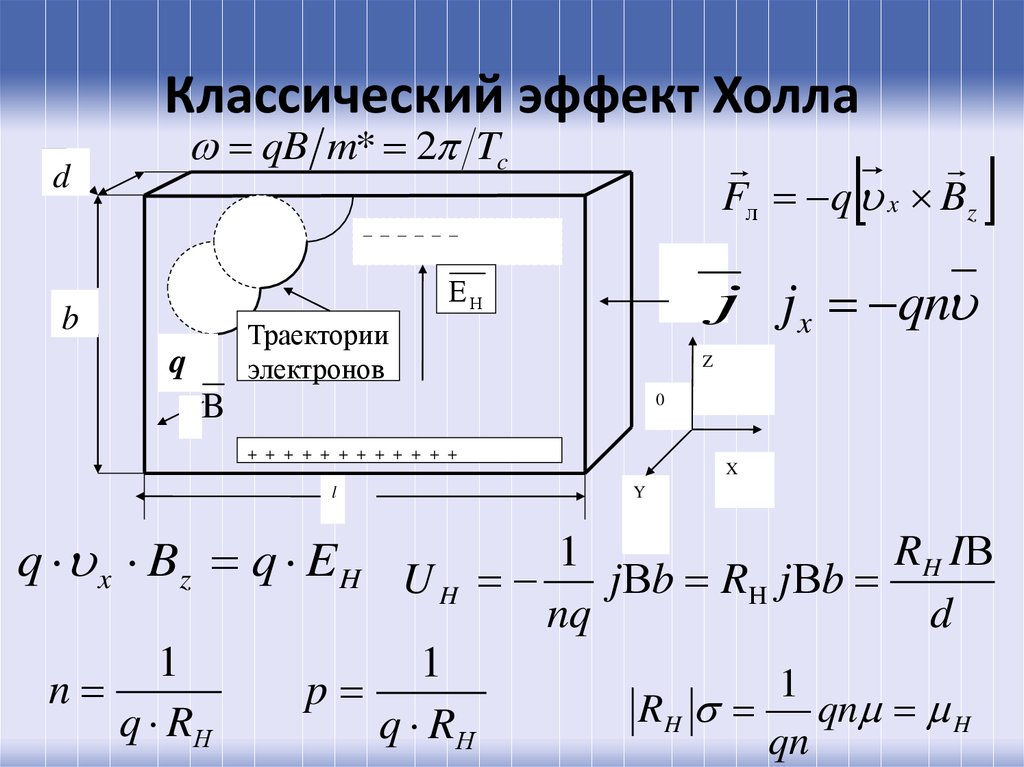
39. Классический эффект Холла
qB m* 2 Tcd
Fл q x Bz
– – – – – –
j jx qn
Н
b
Траектории
электронов
q
Z
B
0
+ + + + + + + + + + + +
X
l
Y
q x Bz q E H U 1 j b R j b RH I
H
H
nq
1
n
q RН
1
p
q RН
d
1
RH
qn H
qn
40.
Важно отметить, что RH — это отношение возникающейпоперечной разности потенциалов к продольному току, RH =
Rxy = Vy/Ix. При этом продольное сопротивление RL = Rxx =
Vx/Ix, слабо зависит от индукции магнитного поля, оставаясь
по величине близким к своему значению при B = 0
Геометрия измерения квантового эффекта Холла. RH=V35/I12
RL=V34/I12
41.
d EFл q d B
Fэп qE y
q d B q E y
EH d B
U H EH b d B b.
42.
I BVx
q n d
1
n
q RН
I B
RН
d
1
p
q RН
43.
j q n dUH
1
j B b R j B b.
nq
1
RН
nq
1
RН
pq
RН H .
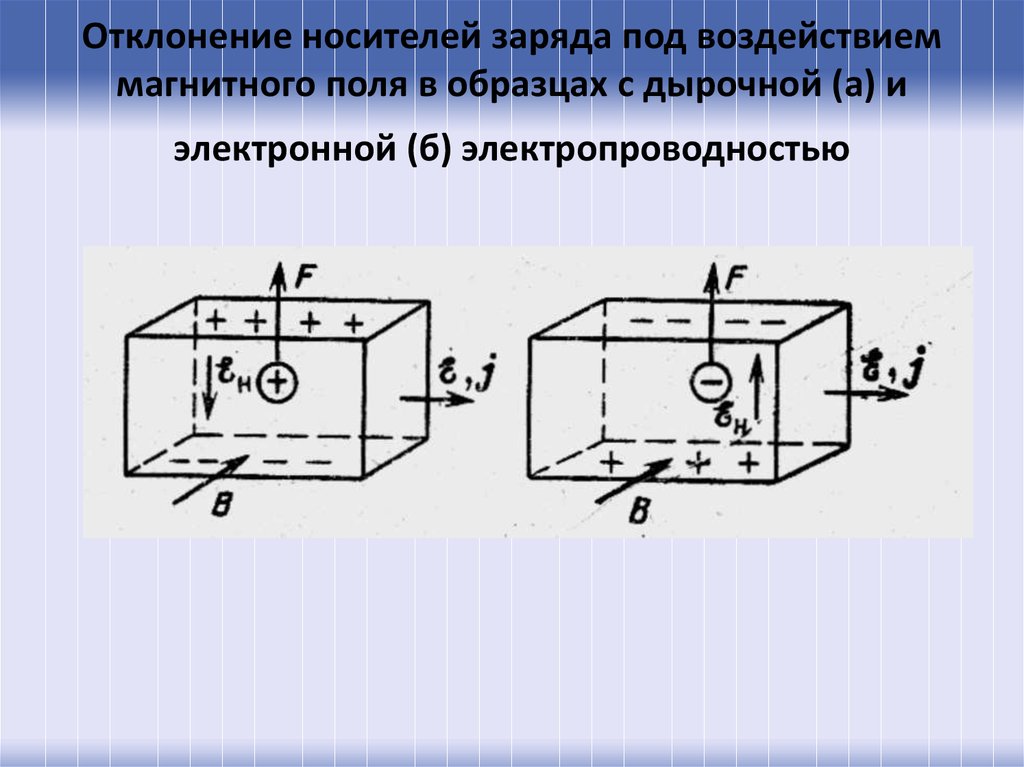
44. Отклонение носителей заряда под воздействием магнитного поля в образцах с дырочной (а) и электронной (б) электропроводностью
45.
Диффузионный и дрейфовый токи46.
Диффузионный и дрейфовый токиОмический ток, который возникает в полупроводниках
при появлении в них электрического поля : j = σ·E можно
разделить на две составляющие:
j nдр q n n E
j pдр q n p E
Носители,
создающие
эти
токи,
дрейфуют
в
электрическом поле на фоне хаотического броуновского
движения, поэтому эти токи называют дрейфовыми
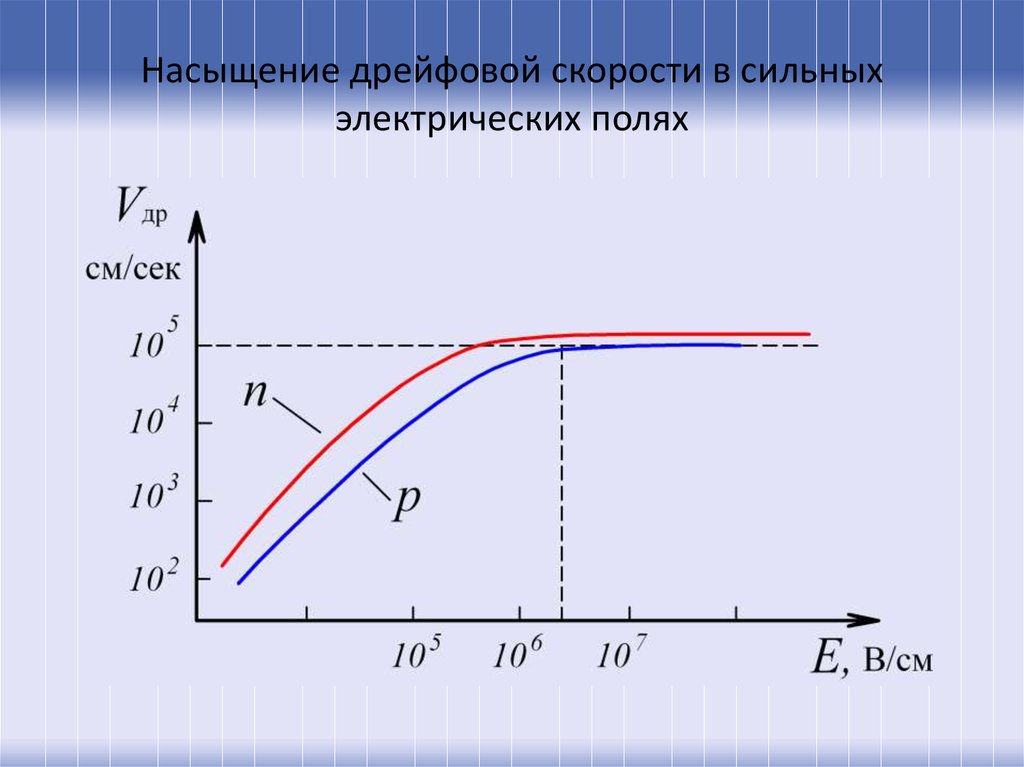
47. Насыщение дрейфовой скорости в сильных электрических полях
48.
Находящиеся в тепловом движении носители заряда вкристалле можно рассматривать как электронный газ. В газах
наблюдается и хорошо изучен процесс диффузии.
Аналогичный эффект должен наблюдаться для
свободных электронов и дырок. Если в какой-то области
возник избыток носителей заряда (градиент концентрации
.grad n n x dn dx ), то под действием диффузии они
должны распространяться из области с большей
концентрацией в область с меньшей концентрацией
49. Диффузионный ток
Соотношение Эйнштейна50.
Градиенты концентрации и диффузионныеэлектронов и дырок направлены в одну сторону
потоки
Образуемые ими диффузионные токи будут протекать в
противоположных направлениях, компенсируя друг друга
В полупроводниковом кристалле перенос заряда всегда
осуществляется в результате двух процессов: дрейфа и
диффузии. Поскольку диффундируют и дрейфуют два тип
носителей заряда должно быть, как минимум, четыре
различных составляющих общего тока: дрейфовый ток
электронов и дырок, диффузионный ток электронов и
дырок
51. Расчёт токов
52.
Неравновесные носителив электрическом поле
53. Основные уравнения
x y z54.
Эти уравнения будут применяться для анализаквазинейтральных областей полупроводниковых приборов, где
избыточные концентрации электронов и дырок
n n n0 p p p0
Квазинейтральность
обеспечивается
кулоновским
притяжением избыточных электронов и избыточных дырок.
При ее нарушении возникает электрическое поле,
напряженность которого определяется уравнением:
E
ρ
s 0
q p n
s 0
Это поле направлено так, чтобы восстановить локальную
неоднородность полпроводника.
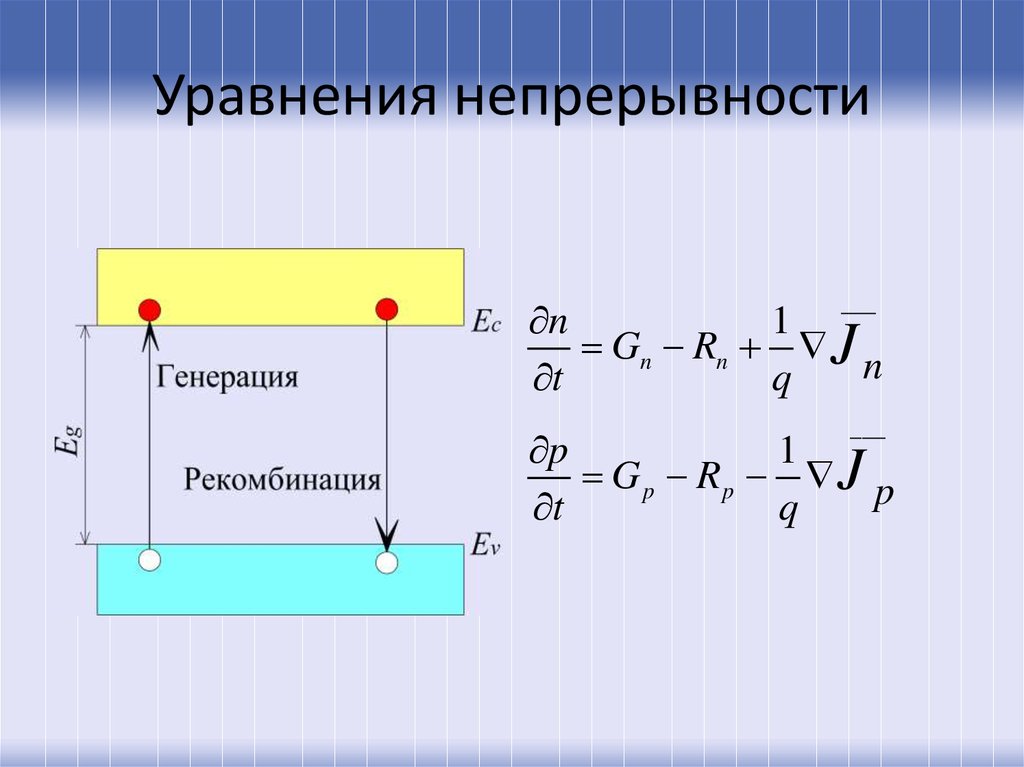
55. Уравнения непрерывности
n1
Gn Rn J
n
t
q
___
___
p
1
Gp Rp J p
t
q
56.
Можно ввести избыточную скорость рекомбинации:n p
G R
t
t
В случае линейной рекомбинации:
n n0 n n n 1
jn
t
t
t
n q
p p0 p p p 1
jp ,
t
t
t
p q
57.
В одномерном случае:n x
n x 1 j n x
t
n
q x
p x
p x 1 j p x
,
t
p
q x
dn
j n j n др j n диф q n n q Dn
dx
dp
j p j p др j p диф q p p q D p
dx
58.
n xn x
2 n x
E x
n x
Dn
n n x
n E x
2
t
n
x
x
x
p x
p x
2 p x
E x
p x
Dp
p p x
p E x
,
2
t
p
x
x
x
Уравнения устанавливают связь между концентрацией
носителей заряда и основными, влияющими на них,
процессами:
диффузией,
дрейфом,
генерацией
и
рекомбинацией. Они позволяют по известным значениям
потенциала
(или
напряженности
поля)
рассчитать
пространственное распределение носителей заряда и его
изменение со временем
59. Переход к биполярным уравнениям
60. Расчет при разных уровнях инжекции
61.
Полупроводниковые приборы состоят, в основном излегированных областей p- или n-типа, при низких
напряженностях электрического поля (при низких уровнях
инжекции) концентрация основных носителей изменяется
слабо, поэтому характер протекающих в этих материалах
процессов будет определяться, в основном, неосновными
носителями заряда .
62. Расчет в стационарных условиях
63. Окончание расчета
64.
Эти уравнения будут широко использоваться при анализепроцессов в таких полупроводниковых приборах, как
биполярные транзисторы и диоды.
Причем для p–области будем использовать уравнение для
неосновных носителей – электронов, для n–области для
дырок.
Уравнение для носителей противоположного знака
решать не будем, полагая, что соблюдается условие
квазиэлектронейтральности и Δp=Δn .


























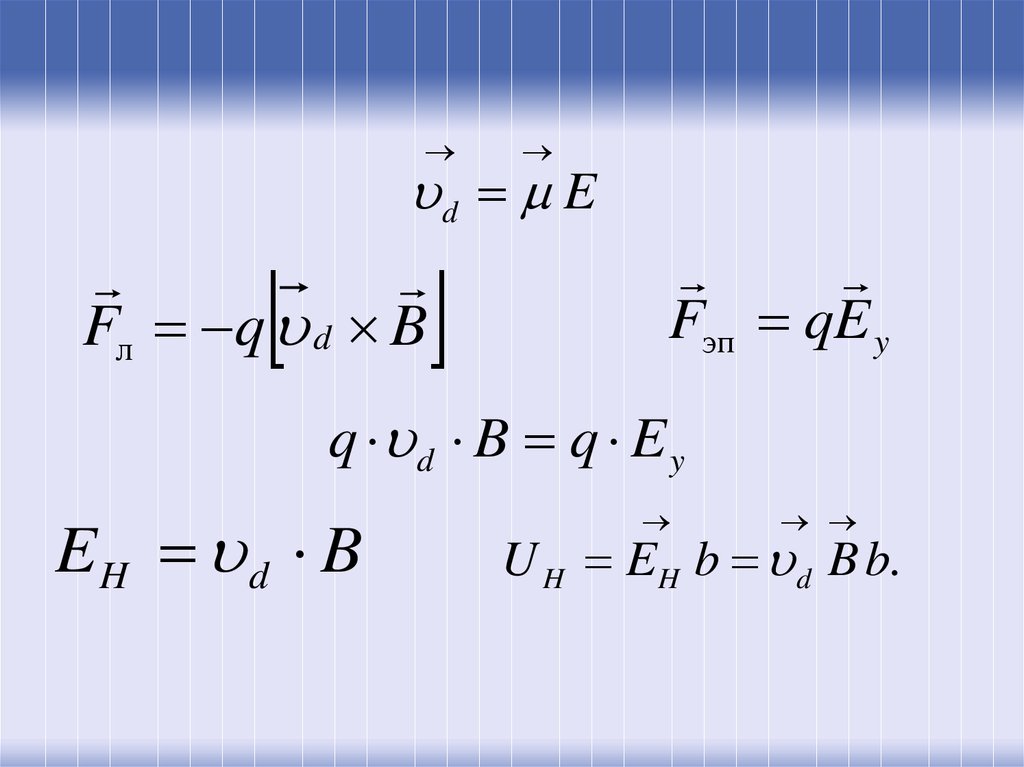




















 physics
physics








