Векторная алгебра

1. Векторная алгебра

Скалярное
произведение векторов
Векторное произведение векторов
Смешанное произведение векторов

2. Скалярное произведение векторов

Определение скалярного произведения векторов
Свойства скалярного произведения векторов
Скалярное произведение векторов в
координатной форме
Условие перпендикулярности векторов
Нахождение угла между векторами
Физическое приложение скалярного
произведения векторов

3. Определение скалярного произведения векторов

Скалярным
произведением
векторов a и b
называется число, равное
произведению модулей
перемножаемых векторов
на косинус угла между
ними. Скалярное
произведение
обозначается символом a.b
.
ab a b cos

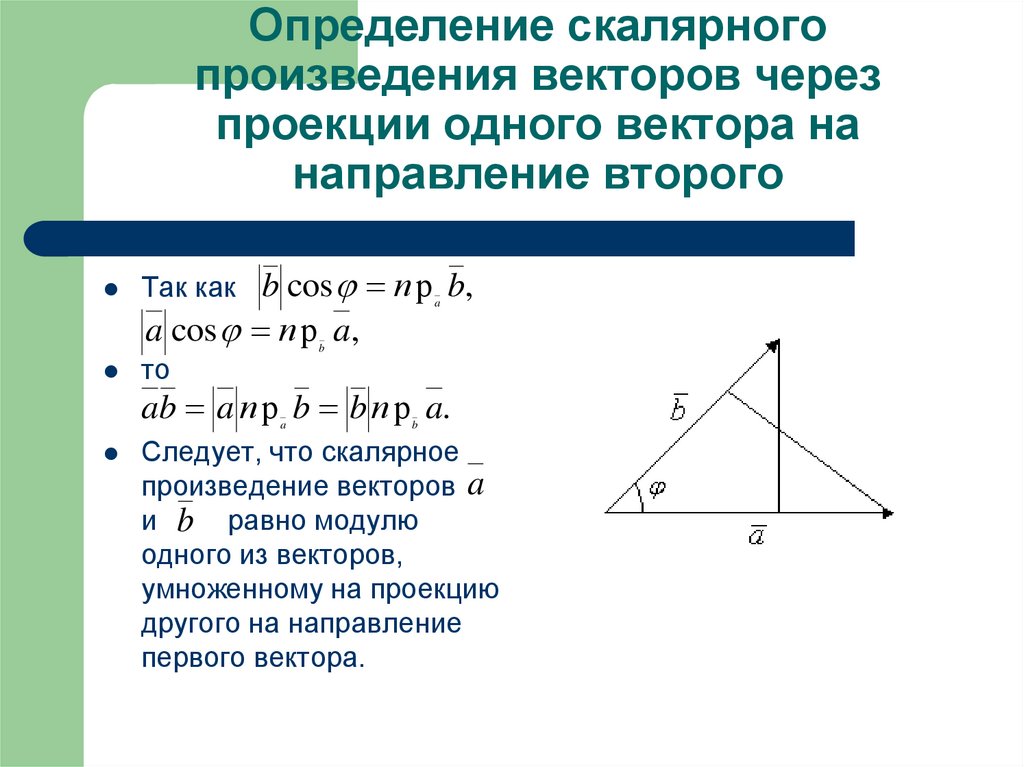
4. Определение скалярного произведения векторов через проекции одного вектора на направление второго

Так как b cos п р b,
a
a cos п р a,
b
то
ab a п р b b п р a.
a
b
Следует, что скалярное
произведение векторов a
и b равно модулю
одного из векторов,
умноженному на проекцию
другого на направление
первого вектора.

5. Свойства скалярного произведения векторов

1) a b b a;
2) ab 0 , если a b или хотя бы один из
векторов есть нулевой вектор
(справедливо и обратное утверждение);
3) a a a ;
4) (ab) ( a)b a( b)
для R;
5) a b c a c b c.
2

6. Скалярное произведение векторов в координатной форме

Пусть векторы a и b заданы своими координатами:
a x i y j z k , b x i y j z k.
1
1
1
2
2
2
Найдем скалярное произведение a b . Вычислим
предварительно скалярные произведения
единичных векторов.
Имеем ii i i cos 0 1 1 1 1, j j 1, k k 1.
Векторы i, j, k взаимно перпендикулярны. Тогда,
согласно свойству 2, их произведения друг на друга
равны нулю. Итак, ab x x y y z z .
1
2
1
2
1
2

7. Условие перпендикулярности векторов

Следствие 1. Если ,
2
то ab 0
Условие x x y y z z 0
называется условием
перпендикулярности двух
векторов, если векторы a и
b заданы своими координатами:
a x i y j z k , b x i y j z k.
1
1
1
2
1
1
2
1
2
2
2
2