Similar presentations:
Геометрическая интерпретация преобразований Лоренца
1. Геометрическая интерпретация преобразований Лоренца
2.
• Изобразим оси системы координат K всистеме отсчета К
• Ось ординат
x 0
x
V
x ct
c
x Vt
V2
1 2
c
0
x Vt 0
• Прямая повернутая
• относительно оси Х на угол
V
V
tgβ , β arctg
c
c
3.
• Аналогично для оси,
t 0
V
t 2 x
c
t
0
2
V
1 2
c
t
,
.
V
t 2 x 0
c
V
ct x
c
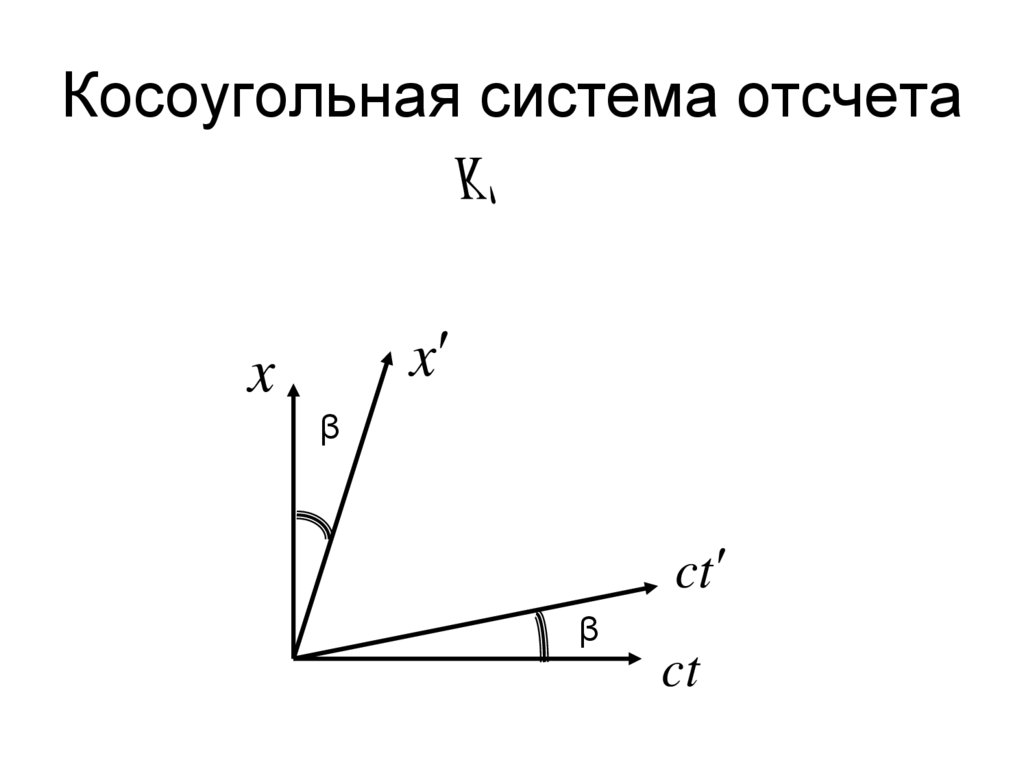
4. Косоугольная система отсчета
Kx
x
β
ct
β
ct
5.
• Проградуируем оси K• Применим инвариантность интервала
2
2
c t x c (t ) ( x )
2 2
2
2
• Точка с координатами
x 0 , ct=1
c t x 1
2 2
2
Гипербола точка А
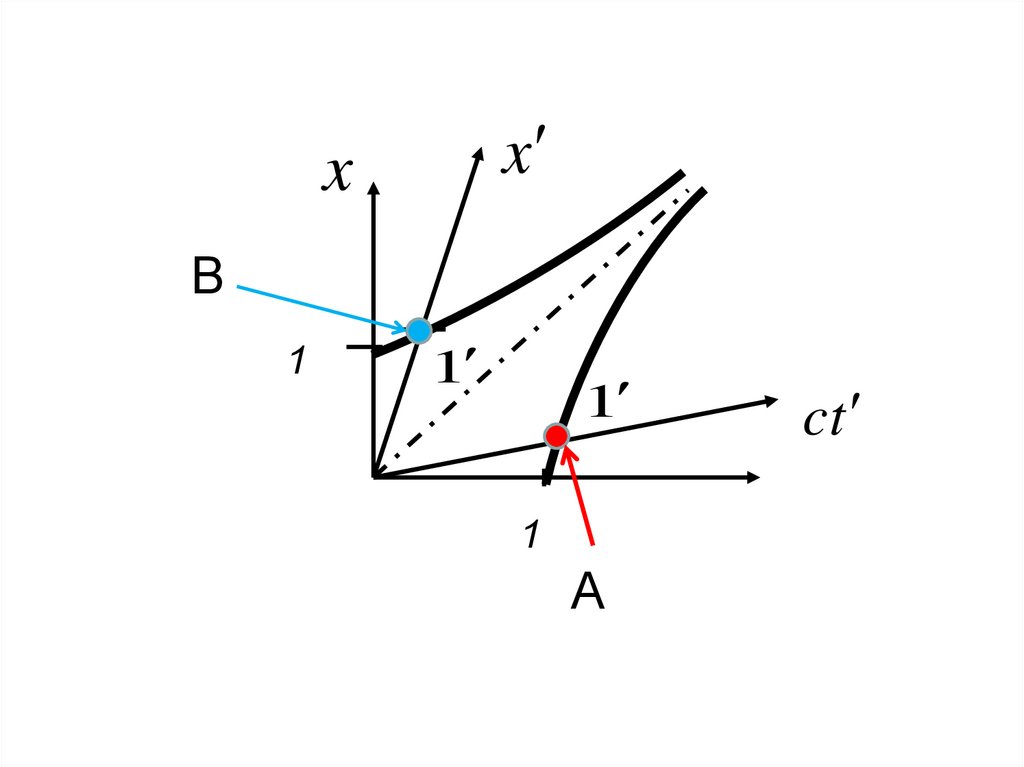
6.
xx
В
1
1
1
1
А
ct
7.
• Аналогично для осиX
x 1 , ct =0
c t x 1
2 2
2
Точка В
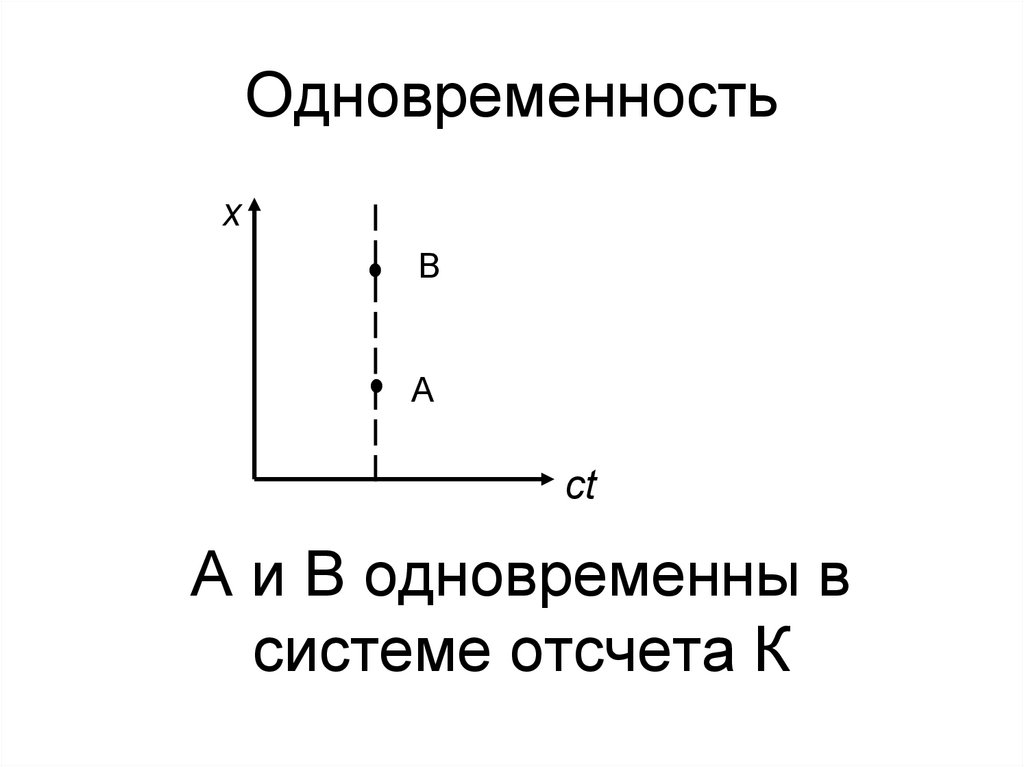
8. Одновременность
xВ
A
ct
А и В одновременны в
системе отсчета К
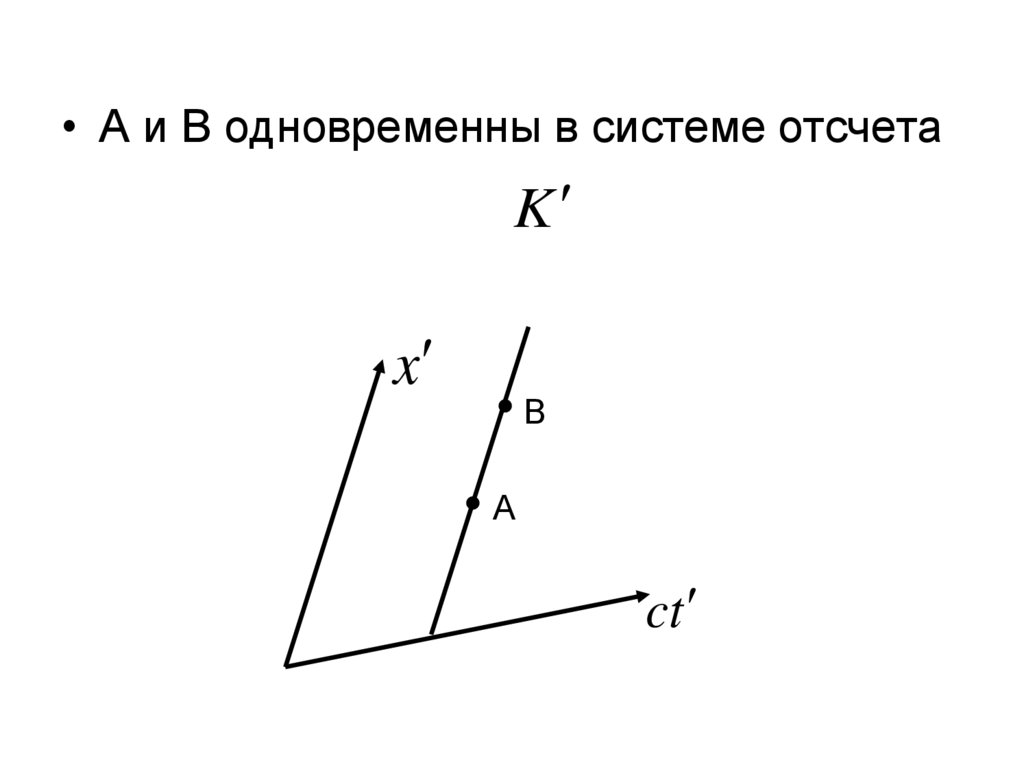
9.
• А и В одновременны в системе отсчетаK
x
В
А
ct
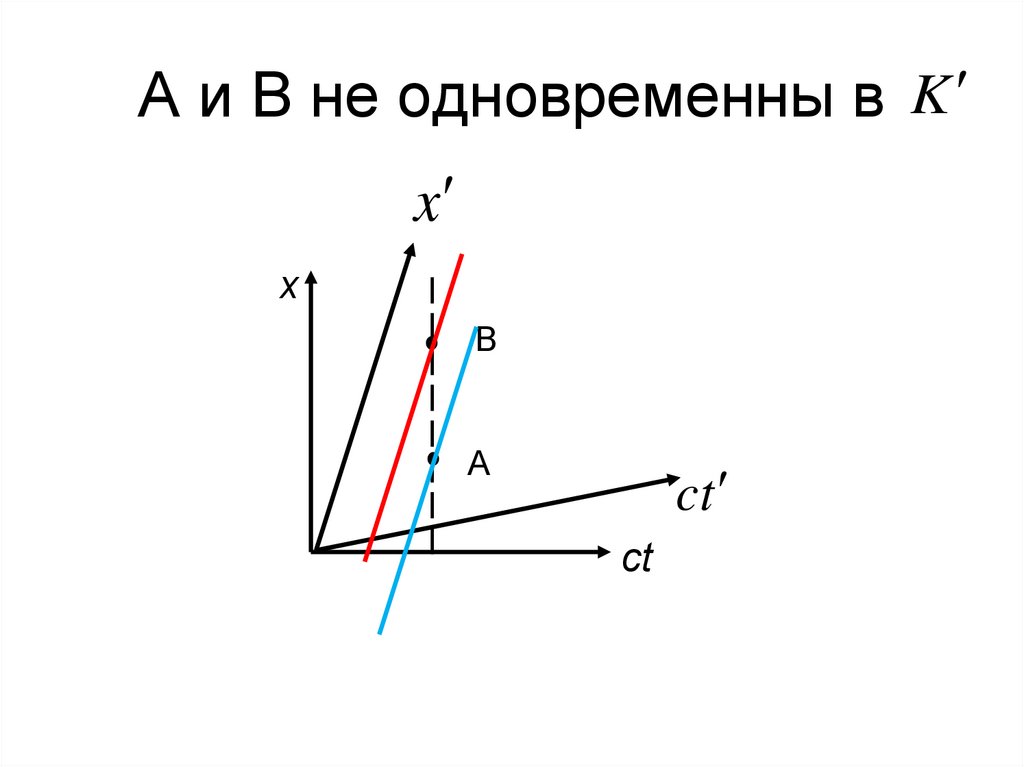
10. А и В не одновременны в
Kx
x
В
A
ct
ct
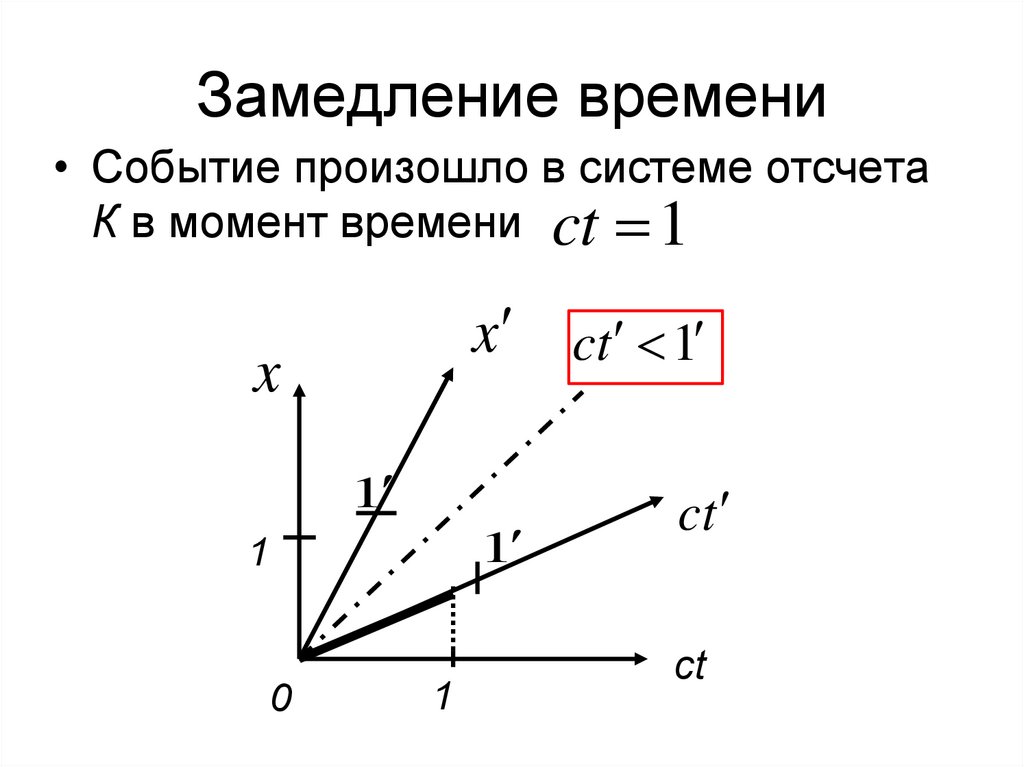
11. Замедление времени
• Событие произошло в системе отсчетаК в момент времени ct 1
x ct 1
x
1
1
1
0
1
ct
ct
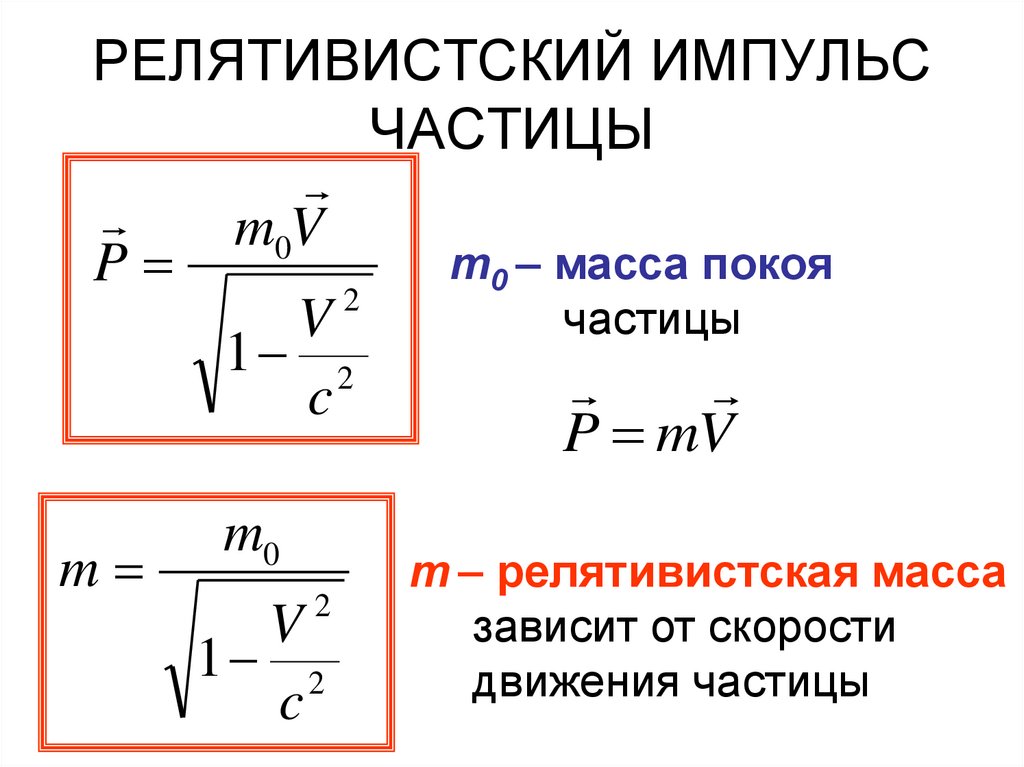
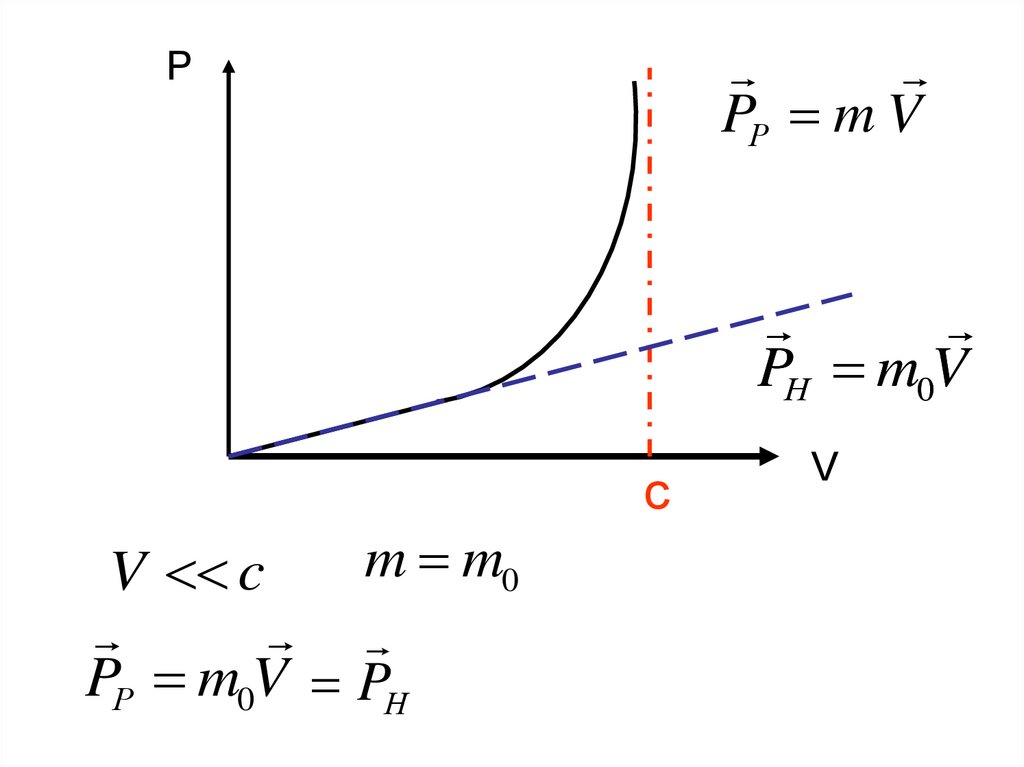
12. РЕЛЯТИВИСТСКИЙ ИМПУЛЬС ЧАСТИЦЫ
m0Vm0 – масса покоя
P
2
частицы
V
1 2
c
P mV
m
m0
2
V
1 2
c
m – релятивистская масса
зависит от скорости
движения частицы
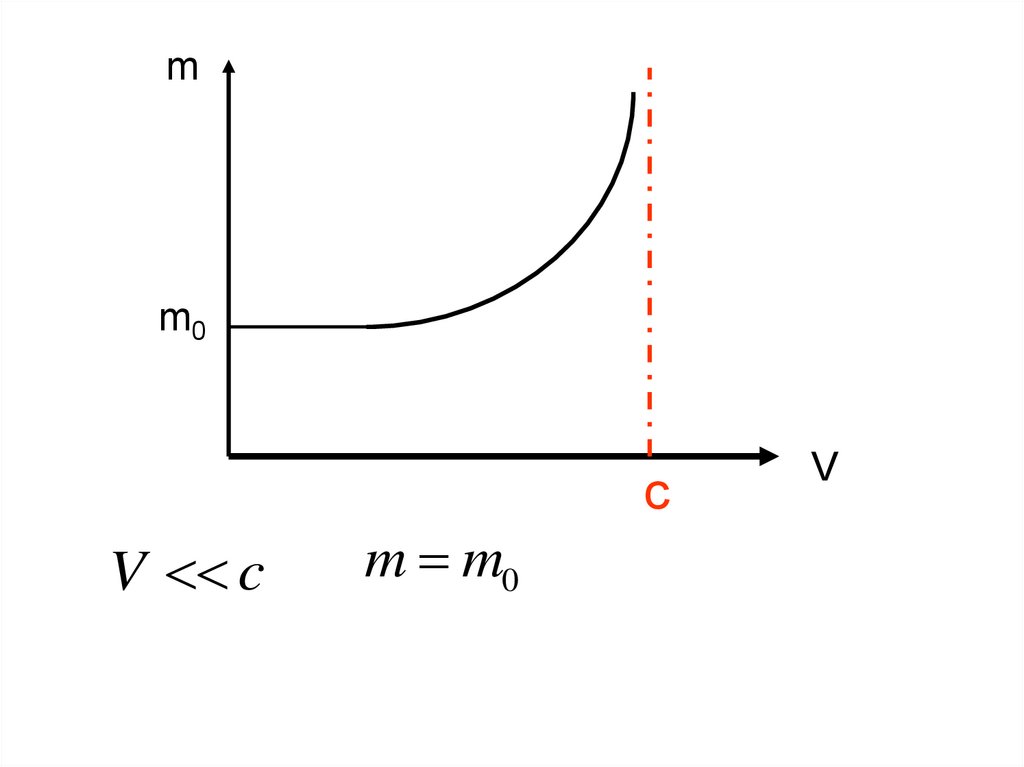
13.
mm0
c
V c
m m0
V
14.
PР m VP
PН m0V
c
m m0
V c
PР m0V PН
V
15. Основной закон релятивистской динамики
dP d (mV ) dmdV
V m
F
dt
dt
dt
dt
dV
dm
a
V ma
F
dt
dt
16.
Fdm
V
dt
ma
a
F
17. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ РЕЛЯТИВИСТСКОЙ ЧАСТИЦЫ
• Определим кинетическую энергию также, как в классической механике
dT dA F dr F Vdt
Fdt V
18.
• Основное уравнение динамикиdP dm
dV
F
V m
dt
dt
dt
Fdt Vdm mdV
Fdt V (V V )dm m(dV V )
V dm mVdV
2
dT
19.
• С другой стороныV
m 1 2
c
2
2
m c 1 V
2 2
2
m
m c
2 2
0
2 2
0
2
2
V
1 2
c
2
m0
m c m c m V
2 2
m0
2
20.
m c m c m V2 2
2 2
0
2
2
d ( m c ) d (m c ) d (m V )
2 2
2 2
0
2
2
2mc dm d ( m c ) 2mV 2 dm 2m 2VdV
2
2 2
0
c dm V dm mVdV
2
2
c dm dT
2
21.
mc
T
2
dm dT
m0
0
T mc m0 c
2
T
m0 c
2
2
V
1 2
c
2
m0 c
Кинетическая энергия
2
22.
• При малых скоростях2
1
2
V
1 2
c
1 V
1 2
2 c
1 V
T m0c 1 2
2 c
2
2
m0V
2
m0c
2
2
• Кинетическая энергия в классической
механике
23. Закон взаимосвязи массы и энергии
c dm dT2
• Приращение кинетической энергии
сопровождается пропорциональным
изменением массы тела
• То, что справедливо для одного вида
энергии должно быть справедливо для
остальных
24.
E mcE
m0 c
2
2
V
1 2
c
2
25.
E T E0E0 m0 c
2
Энергия покоя частицы
• Кинетическая
энергия – это
разность между
полной энергией
и энергией покоя
T E E0
26.
• Масса – мера энергосодержания• Изменение полной энергии тела
сопровождается изменением его массы
E mc
2
27. ПРИМЕР
• Найти изменение массы 1 л воды принагревании от 0 до 100º
E
m 2
c
E mc p t
28.
1000кгm 10 м
3
м
3
3
Дж
c p 4.2 10
кг градус
3
t 100
3
E 10 1000 4.2 10 100
3
4.2 10 Дж
5
29.
E4,2 10
16
0,5 10 кг
m 2
8 2
(3 10 )
c
5
30. Связь между энергией и импульсом
EPc
m0 c
2
E (m0 c ) ( Pc)
2
2 2
2
31.
E (m0c ) ( Pc)2 2
2
Для частиц с нулевой массой покоя ( фотон)
E Pc
32. ПРИМЕНЕНИЕ ЗАКОНОВ СОХРАНЕНИЯ В РЕЛЯТИВИСТСКОЙ МЕХАНИКЕ (ЗАДАЧА О РАСПАДЕ)
33. Законы сохранения энергии и импульса в теории относительности
• При взаимодействии несколькихчастиц, при условии , что на систему
частиц не действуют внешние силы,
сохраняется полная энергия частиц и и
полный импульс частиц
E
i
const
Pi const
34.
• Пусть частица массы M0 распалась надве частицы с массами m01 и m02
• Задача решается в системе центра
инерции (СЦИ)
35.
E1E2
Pc Pc
m01c
2
m02c
2
36.
E M 0c2
E1 (m01c ) ( Pc)
2 2
2
E2 (m02c ) ( Pc)
2 2
2
По закону сохранения энергии
E E1 E2
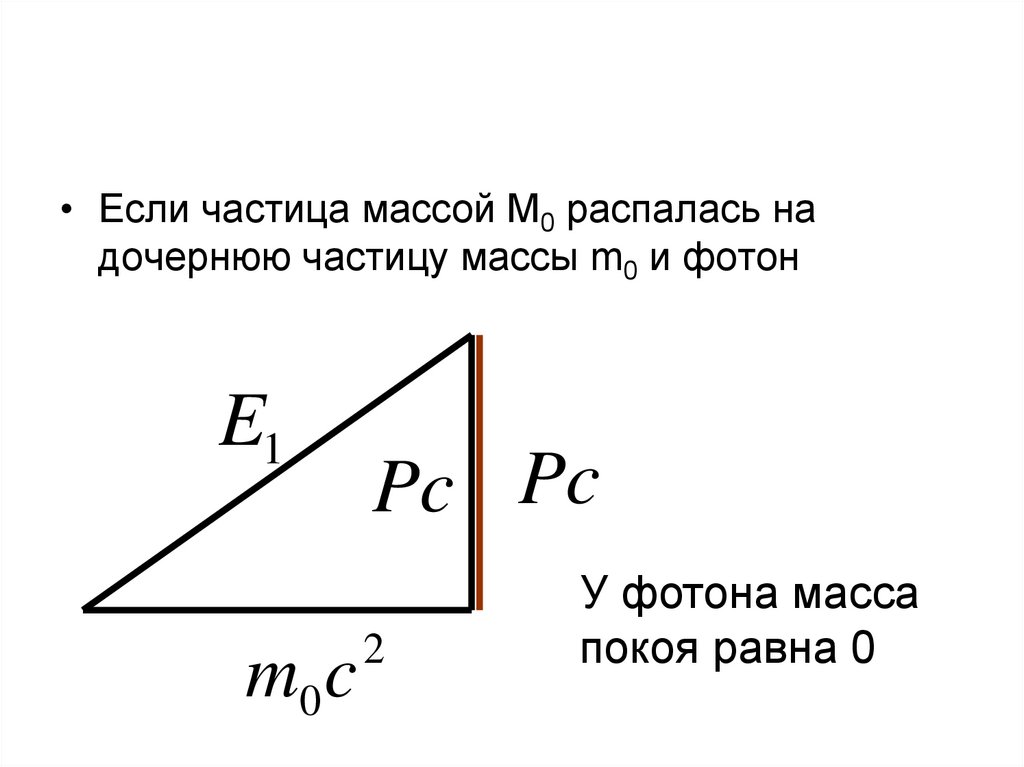
37.
• Если частица массой M0 распалась надочернюю частицу массы m0 и фотон
E1
m0 c
Pc Pc
2
У фотона масса
покоя равна 0
38.
E Mc2
E1 (m0c ) ( Pc)
2 2
2
E Pc
Закон сохранения энергии:
Mc (m1c ) ( Pc) Pc
2
2 2
2









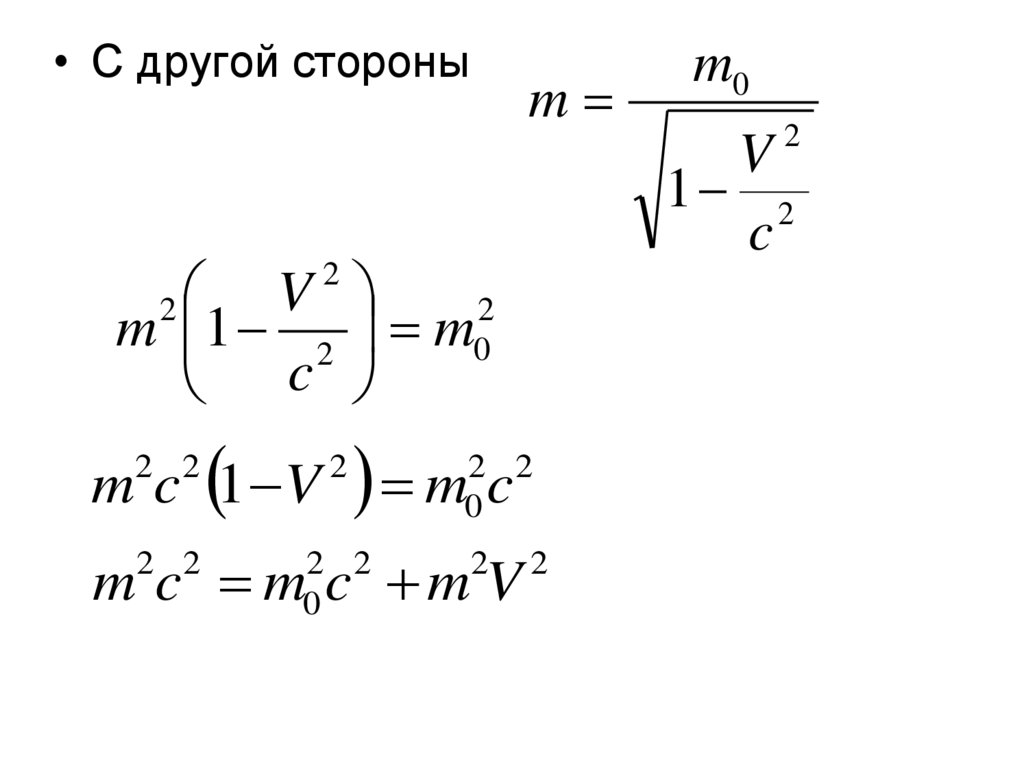




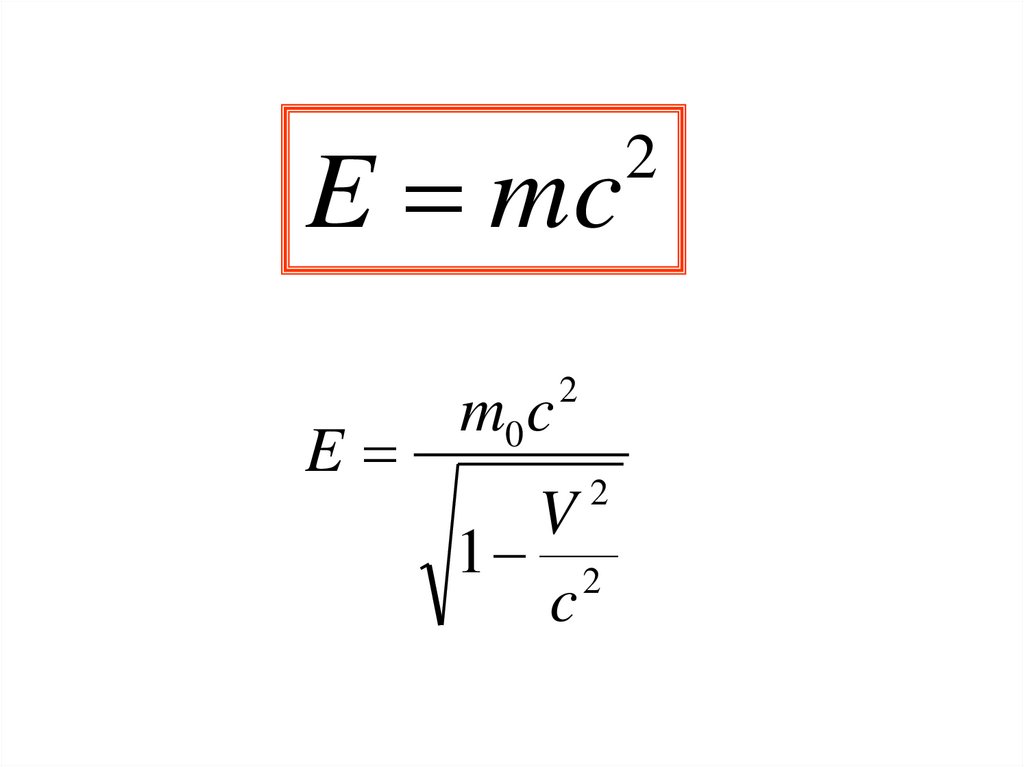



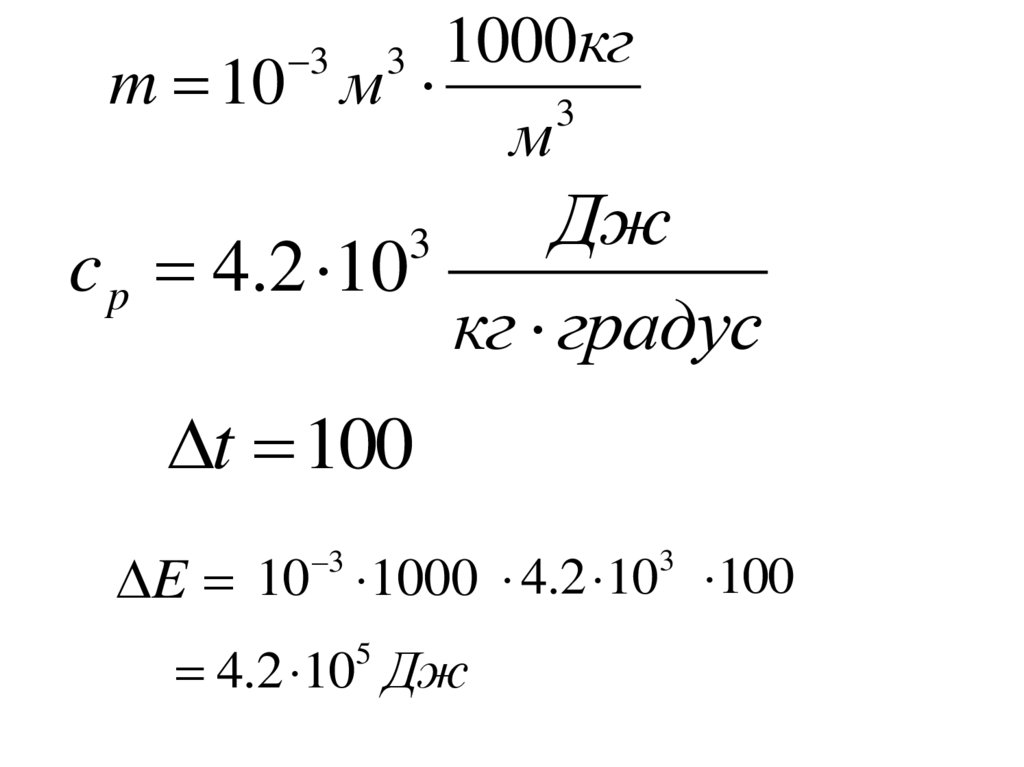
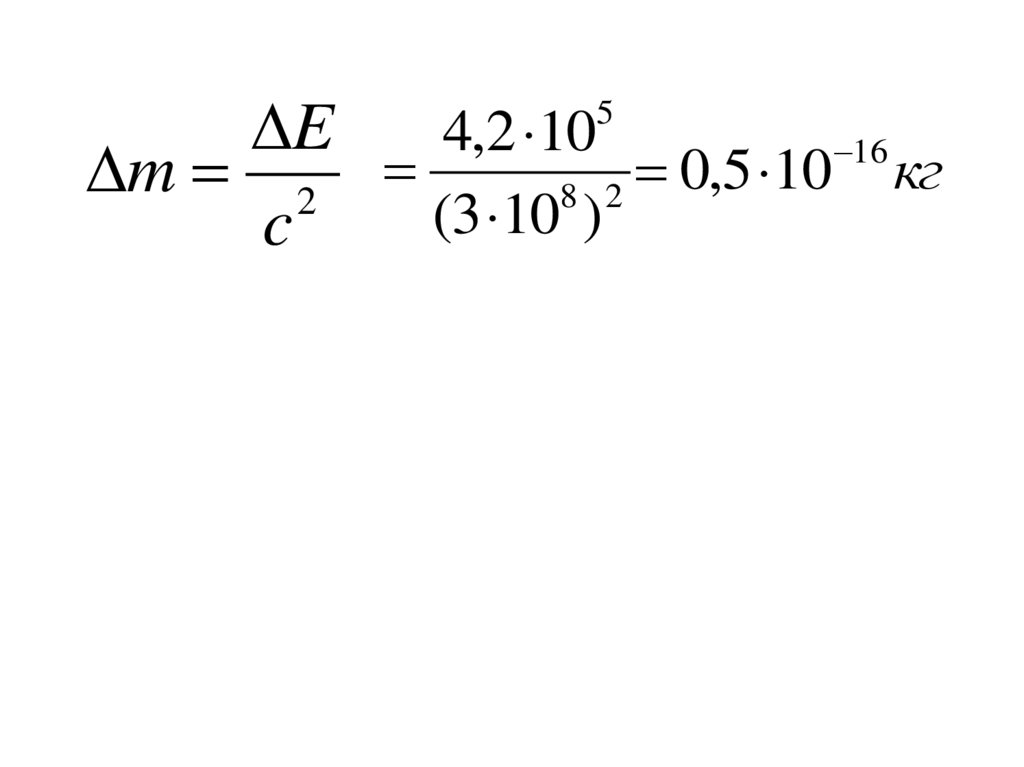

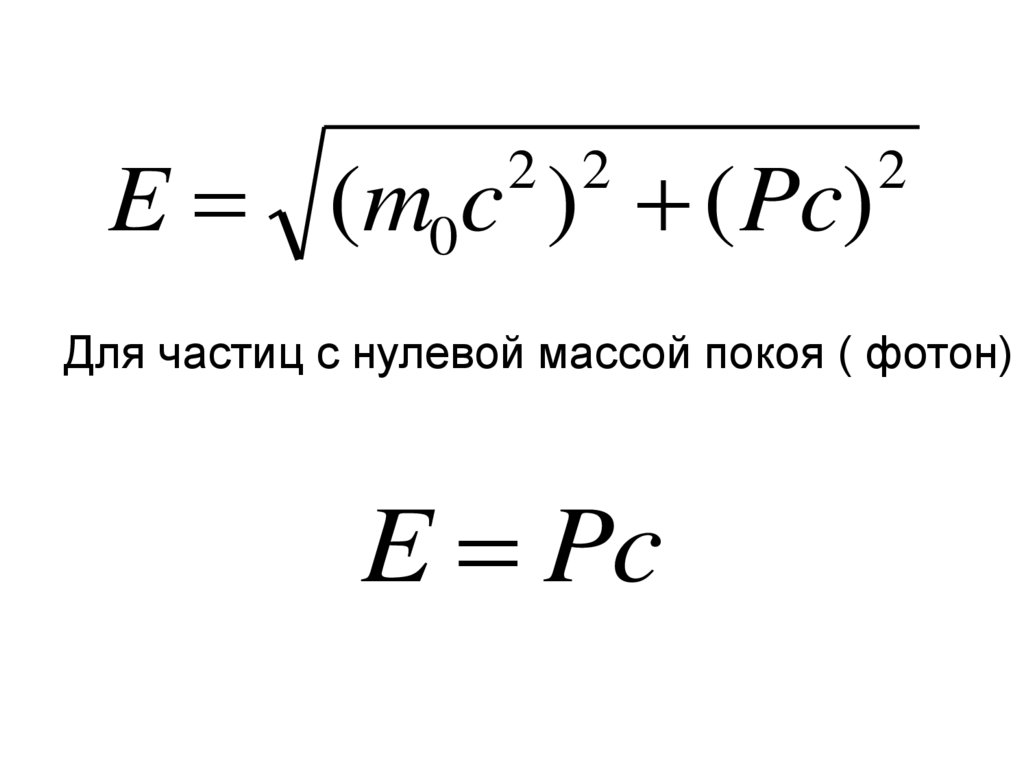



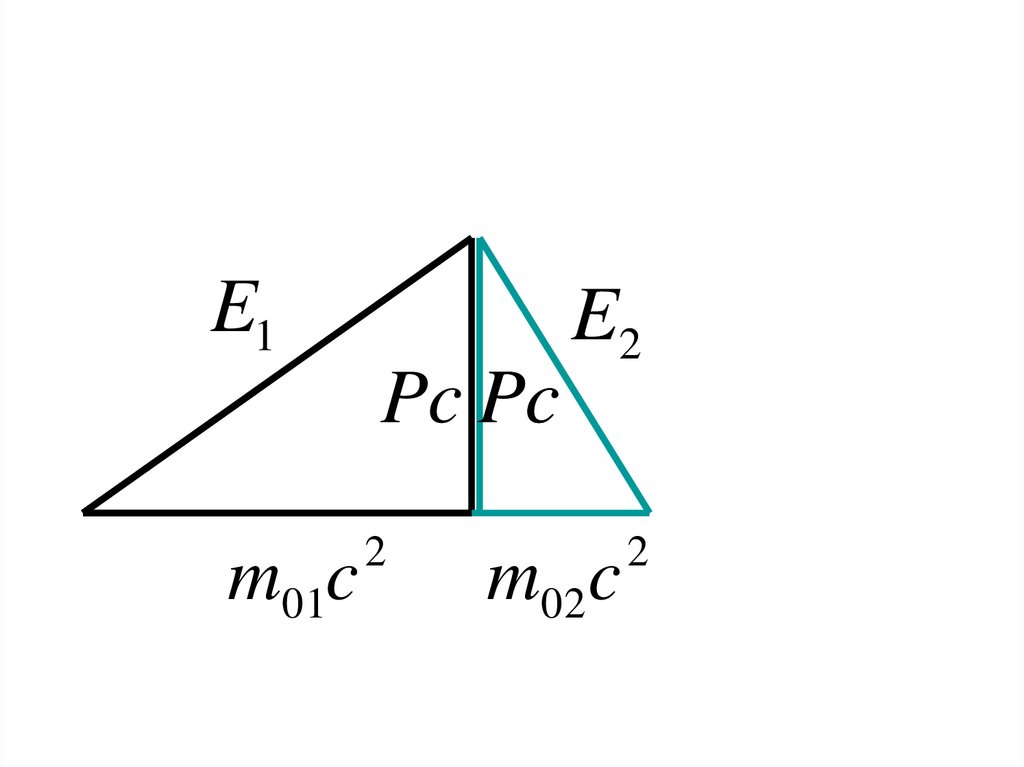

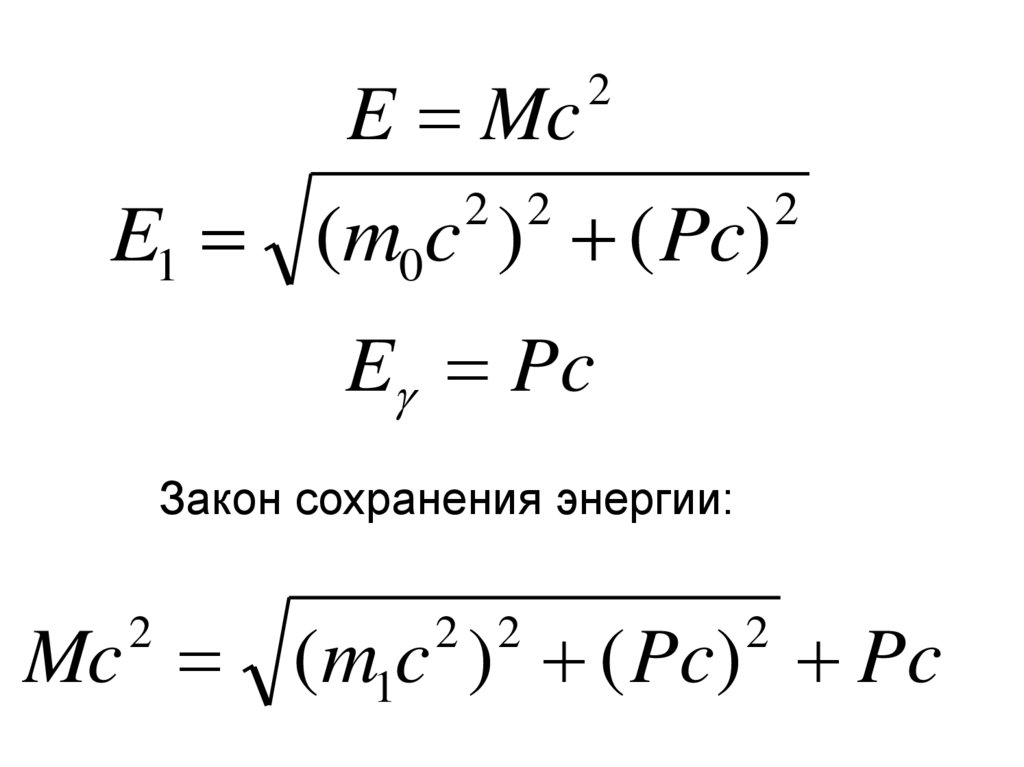
 physics
physics








