Similar presentations:
Основы специальной теории относительности
1. ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
ЕГЭ. ФИЗИКАРЕПЕТИЦИЯ ПО ФИЗИКЕ
Владимир Петрович Сафронов
г. Ростов-на-Дону, 2015
Звоните: т. 8 928 111 7884
Пишите: safron-47@mail.ru
ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ
ОТНОСИТЕЛЬНОСТИ
2. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ (СТО)
раздел механики, в котором изучается движение тел, чьи скоростисоизмеримы со скоростью света.
y
5.1. Принцип относительности Галилея
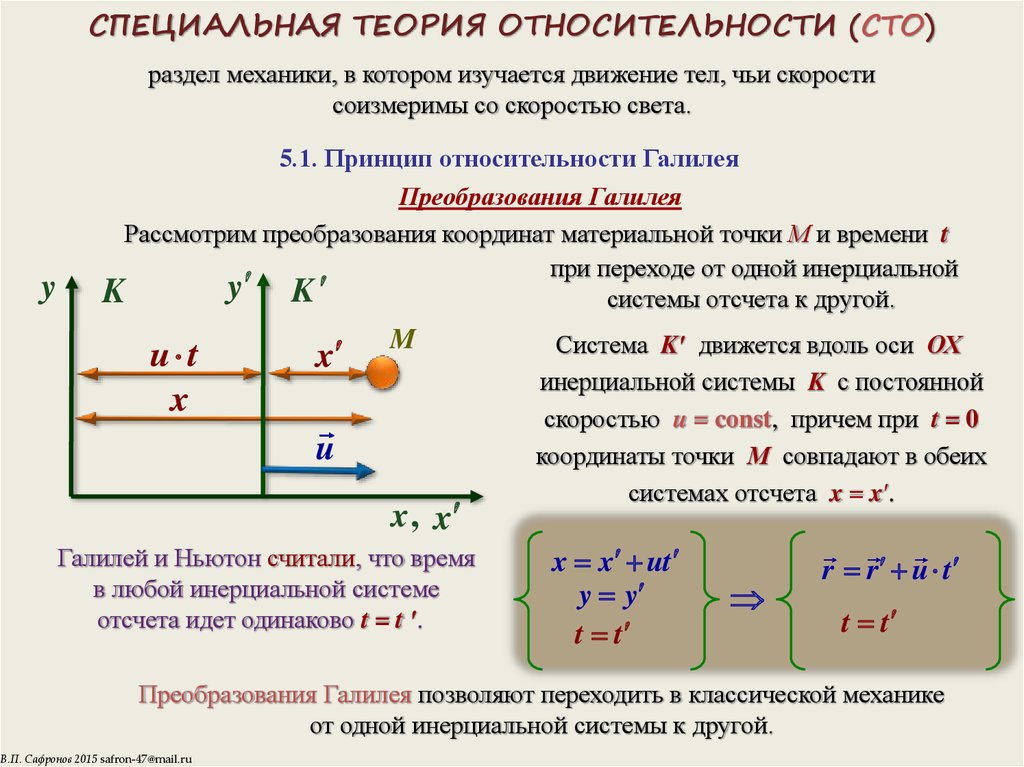
Преобразования Галилея
Рассмотрим преобразования координат материальной точки М и времени t
при переходе от одной инерциальной
y K
K
системы отсчета к другой.
u t
x
x
M
u
x , x
Галилей и Ньютон считали, что время
в любой инерциальной системе
отсчета идет одинаково t = t ′.
Система K′ движется вдоль оси ОХ
инерциальной системы K с постоянной
скоростью u = const, причем при t = 0
координаты точки М совпадают в обеих
системах отсчета x = x′.
x x ut
y y
t t
r r u t
t t
Преобразования Галилея позволяют переходить в классической механике
от одной инерциальной системы к другой.
В.П. Сафронов 2015 safron-47@mail.ru
3. Следствие 1
по времени tr r u t
dr dr
dt , учитывая t = t ′ dr dr
dt
u
u
dt
dt
dt
dt dt
dt
Дифференцируем полученное соотношение
получили закон преобразования скоростей Галилея
при переходе из одной инерциальной системы в другую:
v v u .
Скорость — относительная величина и зависит от выбора системы отсчета.
Следствие 2
Дифференцируем закон преобразования скоростей по времени t
d v d v du , учитывая t = t ′ и u = const,
dt
dt
dt
d v d v
dt
dt
получаем закон преобразования ускорений
a a .
Ускорение не зависит от выбора инерциальной системы отсчета.
Следовательно, сила взаимодействия
F m a
одинакова в любой инерциальной системе отсчета,
если считать , что масса одинакова во всех системах отсчета m = m′.
В.П. Сафронов 2015 safron-47@mail.ru
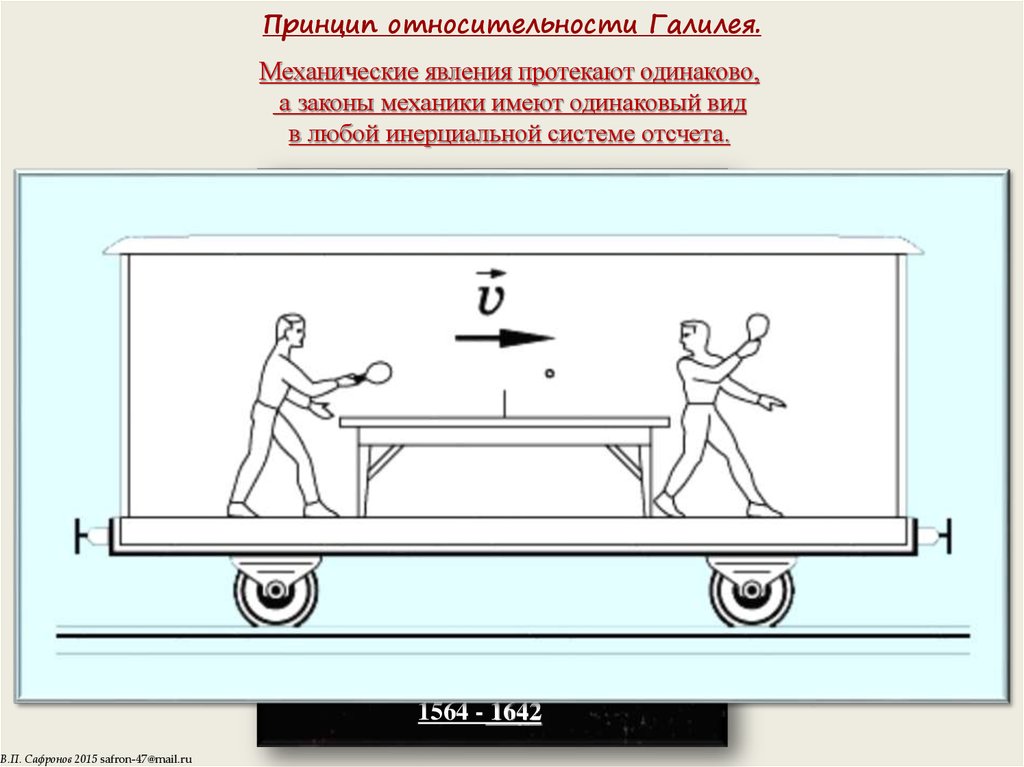
4. Принцип относительности Галилея.
Механические явления протекают одинаково,а законы механики имеют одинаковый вид
в любой инерциальной системе отсчета.
Галилео Галилей
1564 - 1642
В.П. Сафронов 2015 safron-47@mail.ru
5. Принцип относительности Эйнштейна
В классической механике предполагается, что взаимодействиемежду телами осуществляется мгновенно, а, следовательно,
время во всех системах отсчета идет одинаково t = t′.
Это допущение приводит к классическим преобразованиям Галилея.
Однако опыт показывает, что мгновенных взаимодействий не существует.
Значит, есть процесс, осуществляющийся с максимальной скоростью,
быстрее которой материальные объекты двигаться не могут.
Таким процессом является распространение света в вакууме.
Скорость света в вакууме
c 2,998 108 3 10 8 м/с.
Принцип относительности Эйнштейна
Первый постулат
В любых инерциальных системах отсчета все физические явления
при одних и тех же условиях протекают одинаково. Физические законы
имеют одинаковый вид в любой инерциальной системе отсчета.
Второй постулат (принцип инвариантности скорости света)
Скорость света в вакууме не зависит от скорости источника или приемника света.
Принцип постоянства скорости света противоречит
классической механике, а конкретно — закону сложения скоростей.
В.П. Сафронов 2015 safron-47@mail.ru
6. Замедление времени
Эти постулаты привели к изменению классических представленийо времени и пространстве. На их основе Эйнштейном была создана
релятивистская (относительная) механика процессов,
происходящих со скоростями, близкими к скорости света.
СЭМ ВИДИТ, что время у Джона идет медленнее.
ДЖОН
ВИДИТ:
СЭМ ВИДИТ:
ДЖОН
То есть, все процессы в движущейся системе (ДЖОН),
с точки зрения наблюдателя в неподвижной системе (СЭМ),
протекают медленнее (подтверждаются экспериментально).
t
t 0
1
СЭМ
В.П. Сафронов 2015 safron-47@mail.ru
(С – 1) м/с
2
.
v
c2
Промежутки времени, измеряемые часами,
движущимися вместе с объектом t0 ,
называются собственным временем этого объекта.
Неподвижные часы ( t0 СЭМ) идут быстрее
движущихся ( t ДЖОН).
7. Относительность длин (расстояний)
Длина тела зависит от скорости его движения. Длина тела в системе отсчета, гдетело покоится l0, называется собственной длиной и является наибольшей.
Линейный размер тела, движущегося в инерциальной системе отсчета,
уменьшается в направлении движения:
l l0
v2
1 2 .
c
Закон сложения скоростей в релятивистской механике:
v2
v2
v y 1 2
v z 1 2
vx u
c , v
c .
vx
,
v
y
z
1 uv x / c 2
1 uv x / c 2
1 uv x / c 2
При u << c релятивистское преобразование переходит в
закон сложения скоростей классической механики Ньютона:
v v u.
В.П. Сафронов 2015 safron-47@mail.ru
8. Энергия свободной движущейся частицы:
Emc 2
1 v2 c 2
.
Энергия покоя свободной частицы:
E0 mc 2 .
Импульс частицы:
r
r
mv
p
.
2 2
1 v c
Выражение полной энергии через импульс:
E 2 E02 p2c2 .
Если частица не имеет энергии покоя ( фотон E0 = 0), то
E pc.
Эти эффекты заметны лишь при скоростях близких к скорости света.
В.П. Сафронов 2015 safron-47@mail.ru
9. Вывод релятивистской энергии тела
dE dA.Энергия тела растет за счет работы внешней силы
dp
dr
dE Fdr
dr
dp vdp v( md v + vdm ) = mvd v + v 2dm
dt
dt
m
dE dm
vd v v 2 dm ?
dm
m0
m 0vd v
m0
m0
m
dm d
12
32
12
2
2
2
2
2
2
2
2
1 v /c
1 v /c
1 v /c
c2
1 v /c
32
2
2
2
m
v
d
v
1
v
/
c
c
0
2
dE dm
v
12
2
2
m 0vd v 1 v / c
m
m
0
0
dm 1 v / c c v
dm c v v c dm dE
E dE c 2dm
В.П. Сафронов 2015 safron-47@mail.ru
2
2
2
E mc 2 .
2
2
2
2
2








 physics
physics








