Властивості квадратичної функції

1.

2.

3.

Урок №17
Розділ 2.
Тема:
§9. Властивості функції.

4.

УСПІХ
РАДІСТЬ
ОБДАРОВАНІСТЬ
КОМПЕТЕНТНІСТЬ

5.

Домогтися свідомого розуміння змісту
основних понять ,та властивостей
фінкції.
Формувати навички досліджувати фкнкції,
оцінювати область визначення і множину значень
функції,набування додатних та від’ємних значень.
Учні повинні вміти досліджувати
функції.
Розвивати навчальні інтереси ,здібності
на основі розумових дій;формувати
навички аналізу,систематизації,узагальнення
Виховувати культуру математичних міркувань,
уміння тактовно висловлювати свою думку.

6.

Тип уроку :
Обладнання:
Мультимедійна
дошка,проектор,шаблони
функцій,креслярське

7.

№ 329(1). g(1) = 0.
№ 335(1). Д(у) = (-∞;+∞)
№ 335 (4). Д(у) = (-∞;+∞)
№ 335 (5). Д(у) = (-∞;+∞), крім х = -3.

8. “Бліц - опитування ”

1. Ключовим словом в означеннi числової функцiї є…
А) залежнiсть; Б) область визначення; В) число x; Г) число y.
2. Числова функцiя задається:
А) рівнянням y = f(x); Б) областю визначення;
В) аргументом; Г) графiком.
3. У рівнянні y = f(x) число y — це:
А) аргумент; Б) область визначення;
В) функцiя; Г) область значень функцiї.

9.

4. У рівнянні y = f(x) число x — це:
А) аргумент; Б) область визначення;В) функцiя; Г) область значення функцiї.
5. Графiк функції
y = f(x) — це:
А) точка; Б) лiнiя; В) f(x);
Г) множина всiх точок з координатами (x; f(x)).
6. Множина всiх точок з координатами (x; f(x)), де
y = f(x) задана функцiя, — це:
А) точка; Б) лiнiя; В) f(x); Г) графiк функції y = f(x).

10.

Властивостi числових
функцiй
Пригадай! Нулем функцiї називається
значення аргументу, при якому функцiя
дорiвнює нулю.
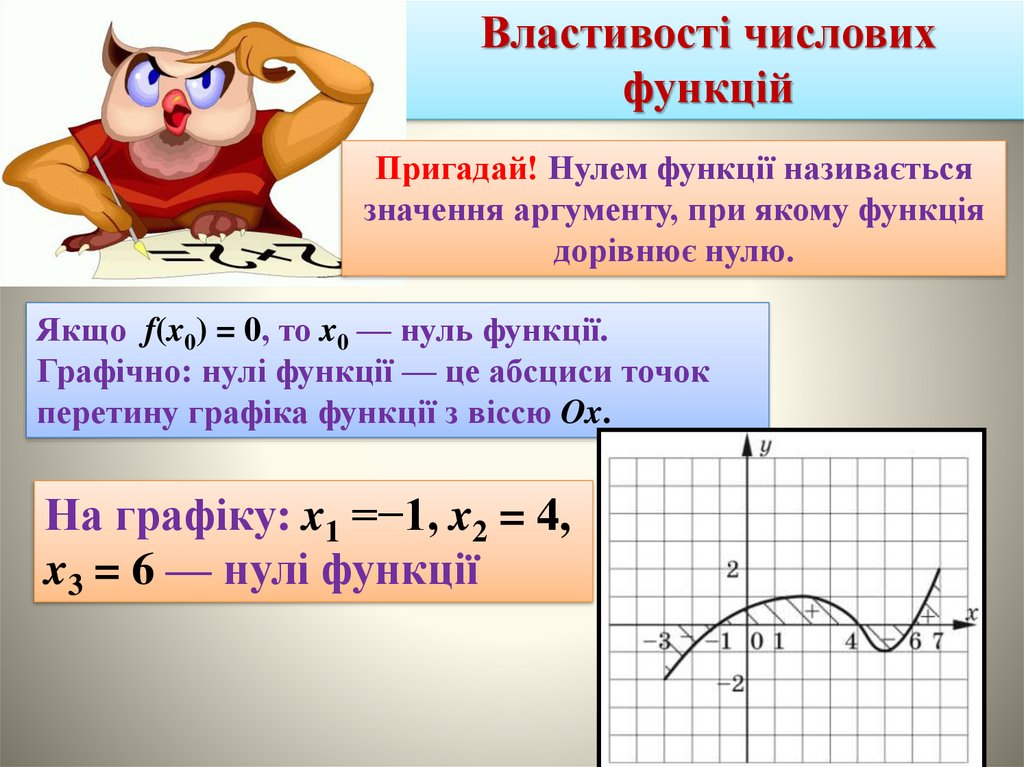
Якщо f(x0) = 0, то x0 — нуль функцiї.
Графiчно: нулi функцiї — це абсциси точок
перетину графiка функцiї з вiссю Ox.
На графiку: x1 =−1, x2 = 4,
x3 = 6 — нулi функцiї

11.

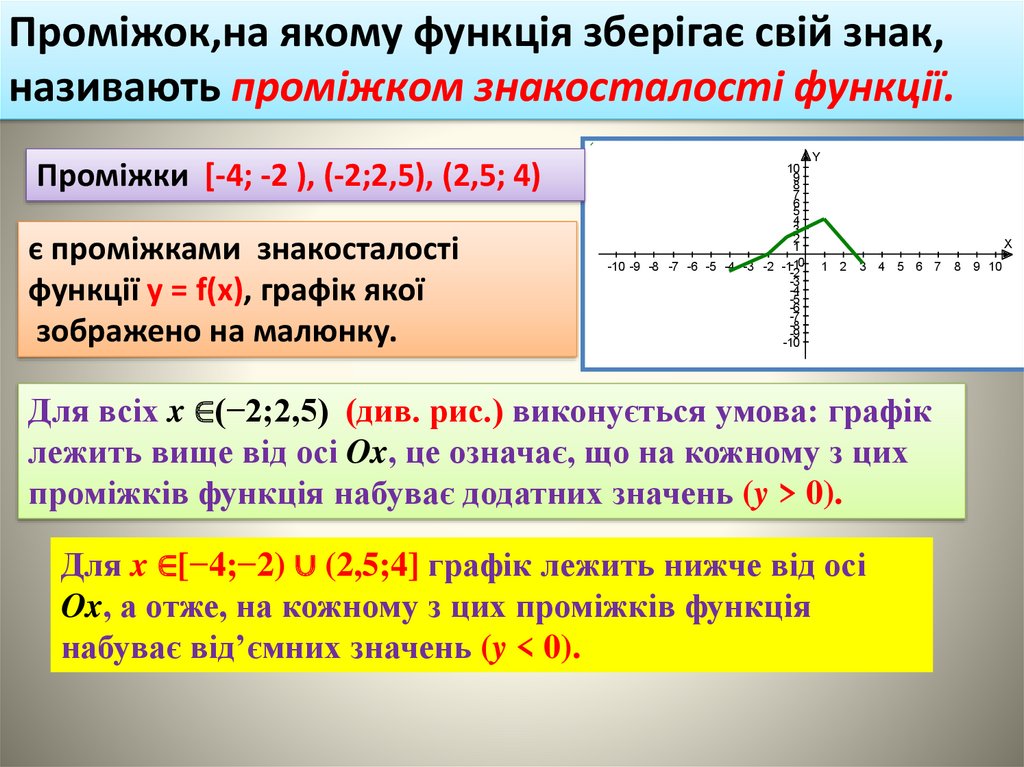
Проміжок,на якому функція зберігає свій знак,
називають проміжком знакосталості функції.
Проміжки [-4; -2 ), (-2;2,5), (2,5; 4)
є проміжками знакосталості
функції у = f(x), графік якої
зображено на малюнку.
10
9
8
7
6
5
4
3
2
1
0
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1-1
-2
-3
-4
-5
-6
-7
-8
-9
-10
Y
X
1 2
3 4 5 6 7
Для всiх x ∈(−2;2,5) (див. рис.) виконується умова: графiк
лежить вище вiд осi Ox, це означає, що на кожному з цих
промiжкiв функцiя набуває додатних значень (y > 0).
Для x ∈[−4;−2) ∪ (2,5;4] графiк лежить нижче вiд осi
Ox, а отже, на кожному з цих промiжкiв функцiя
набуває вiд’ємних значень (y < 0).
8 9 10

12.

Виконання вправ:
Приклад № 363(2). Знайти нулi функції y = 2 - 5х.
Розв’язання:
у = 0 ; 2 – 5х = 0, 2 = 5х, х = 5: 2 = 2,5. х = 2,5 – нуль функції.
Приклад . Знайти проміжки знакосталості функції
y = 3х + 2.

13.

2. Зростання функцiї
Функцію називають зростаючою на деякому промiжку, якщо
бiльшому значенню аргументу з цього промiжку вiдповiдає
більше значення функції.
Функцiя y = f(x) називається зростаючою на промiжку P, якщо
для x1 ∈ P, x2 ∈ P x1 > x2 виконується нерівність
f (x1) < f (x2)
Як за графiком знайти промiжки зростання функцiї?
Заданий проміжок [ -5; 3].
При x ∈ [−5;−3] i x ∈ [1;3] графiк функцiї
y = f(x) «йде» вгору, отже, y = f(x)
зростає;

14.

3. Спадання функцiї
Функцію називають спадаючою на деякому промiжку, якщо
бiльшому значенню аргументу з цього промiжку вiдповiдає
менше значення функції.
Функцiя y = f(x) називається спадаючою на промiжку P, якщо
для x1 ∈ P, x2 ∈ P x1 > x2 виконується нерівність
f (x1) < f (x2)
Як за графiком знайти промiжки спадання функцiї?
Заданий проміжок [ -5; 3].
При x ∈ [−3;1] графiк функцiї y = f(x)
«йде» вниз, отже, y = f(x) спадає.

15.

Приклад. Довести, що функцiя y = x2−1
спадає на промiжку (−∞;0].
Доведення. Нехай x1 i x2 — довiльнi значення аргументу з промiжку (−∞;0],
причому x1 < x2. f (x1), f (x2) — вiдповiднi значення функцiї, тобто
f (x1) = x12−1, f (x2) = x22−1. Розглянемо рiзницю f (x1)−f (x2) = x12−1−(x22−1)
= x12−x22= (x1− x2)(x1+x2).
Оскiльки x1 < x2, то x1 − x2 <0. За умовою x ∈ (−∞;0], тому
x1 ≤ 0, x2 ≤ 0 i x1+x2 < 0.
Отже, (x1−x2)(x1+x2) > 0, тобто f(x1)−f(x2) >0, звiдки дiстанемо, що
f(x1) > f(x2), тобто функцiя y = x2−1 на промiжку (−∞;0] спадає.
.

16.

№ 371. Накресліть схематично графiк
функцiї у = g(x), областю визначення якої є
промiжок [−3;5], так, щоб :
1)
2)
3)
4)
Нулем функції було число 2;
нулями функції були числа -1 і 4;
функція зростала на проміжку [ -3; 2];
Спадала на проміжку [ 2; 5].

17.

Тестовi завдання
1. Функцiя y = f (x) спадна, якщо:
А) x2 < x1; Б) f (x2) < f (x1);
В) при x1 > x2 f (x2) < f (x1);
Г) при x2 < x1 f (x2) < f (x1).
2. Функцiя y = f (x) зростаюча, якщо:
А) при x2 > x1 f (x2) > f (x1); Б) y1 > y2;
В) при x2 > x1 f (x2) < f (x1); Г) x2 > x1.

18.

3. Укажiть промiжок спадання функцiї, графiк якої
зображено на рисунку.
А) [−5;−3]; Б) [−3;−1]; В) [−2;1]; Г) [−3;−2].

19.

Домашнє завдання
Р.2§ 8.Вивчити означення понять, розглянутих на уроцi.
Виконати вправи :
№ 370 (1). Знайдіть нулі функції:
№ 373 ( 1;) . Знайдіть область визначення фінкції:
№ 375. (2) додатково. )
Повторити графіки функцій та їх властивості.

20.

Підсумок уроку.
1. Під час проведення уроку мені сподобалось
2. Свої знання я
3. Я добре
поповнив …
виконав …
4. Я вважаю, що поставлену мету ми…