Теоретическая механика модуль 1. Раздел 2 – кинематика

1.

МЕХАНИКА
Теоретическая механика
Модуль 1
Раздел 2 –
КИНЕМАТИКА
КИНЕМАТИКА ТОЧКИ
КИНЕМАТИКА ТВЕРДОГО
ТЕЛА
СЛОЖНОЕ ДВИЖЕИЕ ТОЧКИ
ПЛОСКОПАРАЛЛЕЛЬНОЕ
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ЛЕКЦИЯ 7
ЛЕКЦИЯ 8
ЛЕКЦИЯ 9
ЛЕКЦИЯ 10
ЛЕКЦИЯ 11
ЛЕКЦИЯ 12
ЛЕКЦИЯ 13

2.

7.2
КИНЕМАТИКА ТОЧКИ
Кинематикой
называется раздел механики, в котором
изучаются геометрические свойства движения тел без учета их
инертности и действующих на них сил.
Траекторией точки называется непрерывная линия,
которую описывает движущаяся точка относительно данной
системы отсчета.
Для задания движения точки можно применять способы:
- векторный;
- координатный;
- естественный.

3.

КИНЕМАТИКА ТОЧКИ
7.3
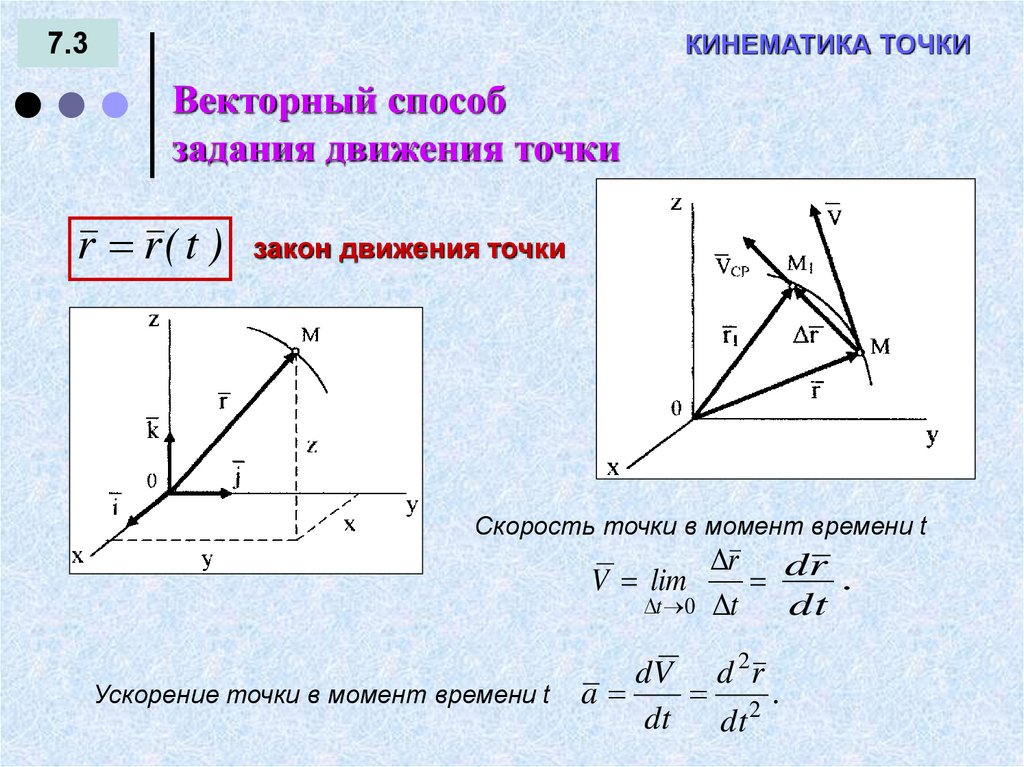
Векторный способ
задания движения точки
r r( t )
закон движения точки
Скорость точки в момент времени t
V lim
t 0
Ускорение точки в момент времени t
r dr
.
dt
t
dV d 2 r
a
2.
dt
dt

4.

КИНЕМАТИКА ТОЧКИ
7.4
Координатный способ
задания движения точки
x = f1(t);
у = f2(t); закон движения точки
z = f3(t).
ускорение точки
скорость точки
dx
vx = dt
dy
vy =
dt
dz
vz = dt
v vx2 v 2y vz2
cos vx / v
cos v y / v
cos vz / v.
dv x d 2 x
ax
,
2
dt dt
a a x2 a 2y a z2
d2y
ay
,
2
dt
dt
cos 1 a x / a ,
dv z d 2 z
az
,
2
dt dt
cos 1 a z / a .
dv y
cos 1 a y / a ,

5.

КИНЕМАТИКА ТОЧКИ
8.2
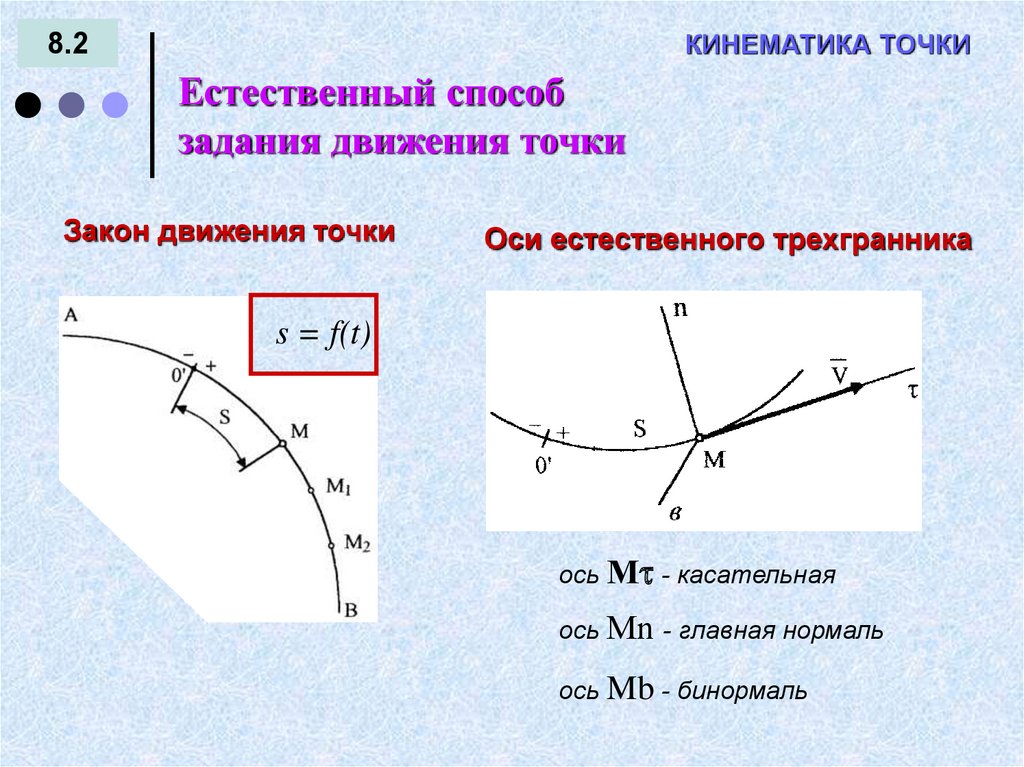
Естественный способ
задания движения точки
Закон движения точки
Оси естественного трехгранника
s = f(t)
ось М - касательная
ось Мn - главная нормаль
ось Mb - бинормаль

6.

КИНЕМАТИКА ТОЧКИ
8.3
Естественный способ
задания движения точки
Скорость точки
Ускорение точки
s
ds
или v
v lim
dt
t 0 t
dv d 2 s
а
2
dt dt
Кривизна траектории
в точке М
k = 1/ ,
ρ = ;
для окружности ρ = R.
v
v2
аn
а a 2 an2
для прямой линии
a
tg
an

7.

КИНЕМАТИКА ТОЧКИ
8.4
Естественный способ
задания движения точки
Частные случаи движения точки
Прямолинейное
движение
=
Тогда
an = v2 / = 0
Полное ускорение :
a = a = dv/dt.
При равномерном
движении
v = const, a = 0,
а=0
Криволинейное
движение
- равномерное движение
v = const
a = dv/dt = 0
a = an = v2/ .
- равнопеременное движение
a = const
an = v2/ .
а a 2 an2

8.

9.2
Простейшие движения твердого тела
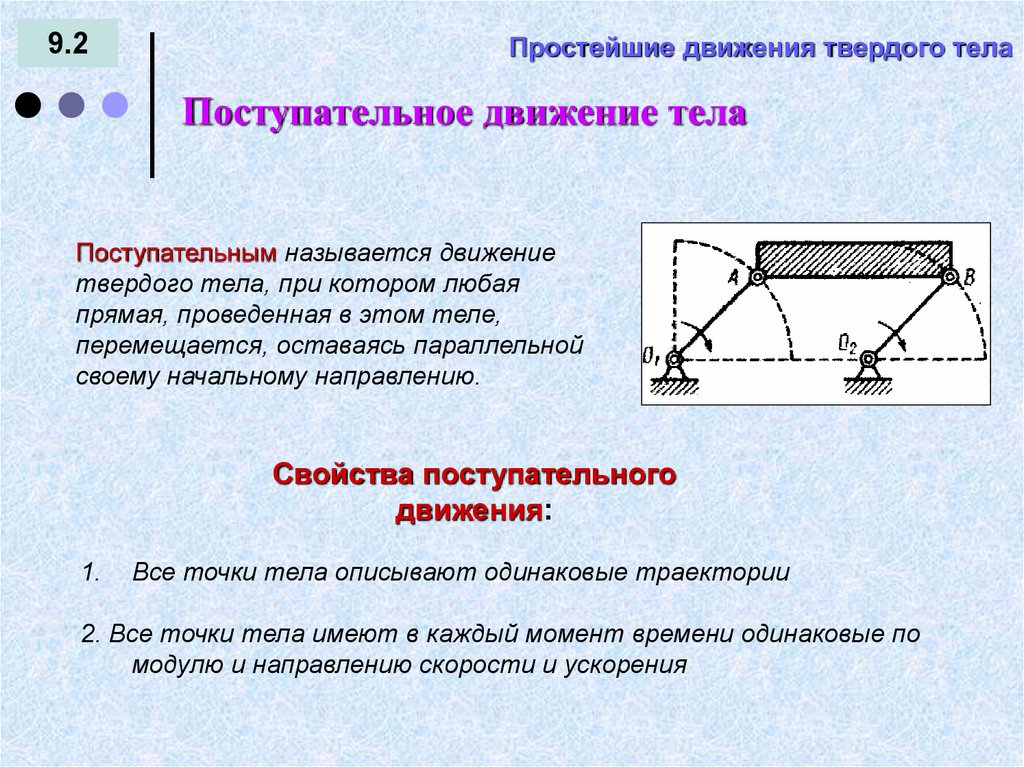
Поступательное движение тела
Поступательным называется движение
твердого тела, при котором любая
прямая, проведенная в этом теле,
перемещается, оставаясь параллельной
своему начальному направлению.
Свойства поступательного
движения:
1.
Все точки тела описывают одинаковые траектории
2. Все точки тела имеют в каждый момент времени одинаковые по
модулю и направлению скорости и ускорения

9.

Простейшие движения твердого тела
9.3
ВРАЩЕНИЕ ТВЁРДОГО ТЕЛА
ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Вращательным движением твердого тела
вокруг неподвижной оси называется
движение, при котором какие-нибудь две
точки, принадлежащие телу (или неизменно
с ним связанные), остаются во все время
движения неподвижными
Проходящая через неподвижные точки
прямая - ось вращения.
=
f(t)
φ - угол поворота тела
закон вращательного движения
твердого тела вокруг неподвижной оси.

10.

Простейшие движения твердого тела
9.4
ВРАЩЕНИЕ ТВЁРДОГО ТЕЛА
ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Угловая скорость тела
d
dt
Единица измерения
рад/с, 1/с, с-1.
Угловое ускорение тела
d d 2
2
dt dt
Единица измерения ε
рад/с2,
1/с2 ,
с-2.

11.

Простейшие движения твердого тела
9.4
ВРАЩЕНИЕ ТВЁРДОГО ТЕЛА
ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Скорости точек вращающегося тела
ds
d
v h
dt
dt
v=h
-линейная или окружная
скорость точки М.
Ускорение точки М
a a 2 an2
а =h , аn = h 2.
а h 2 4

12.

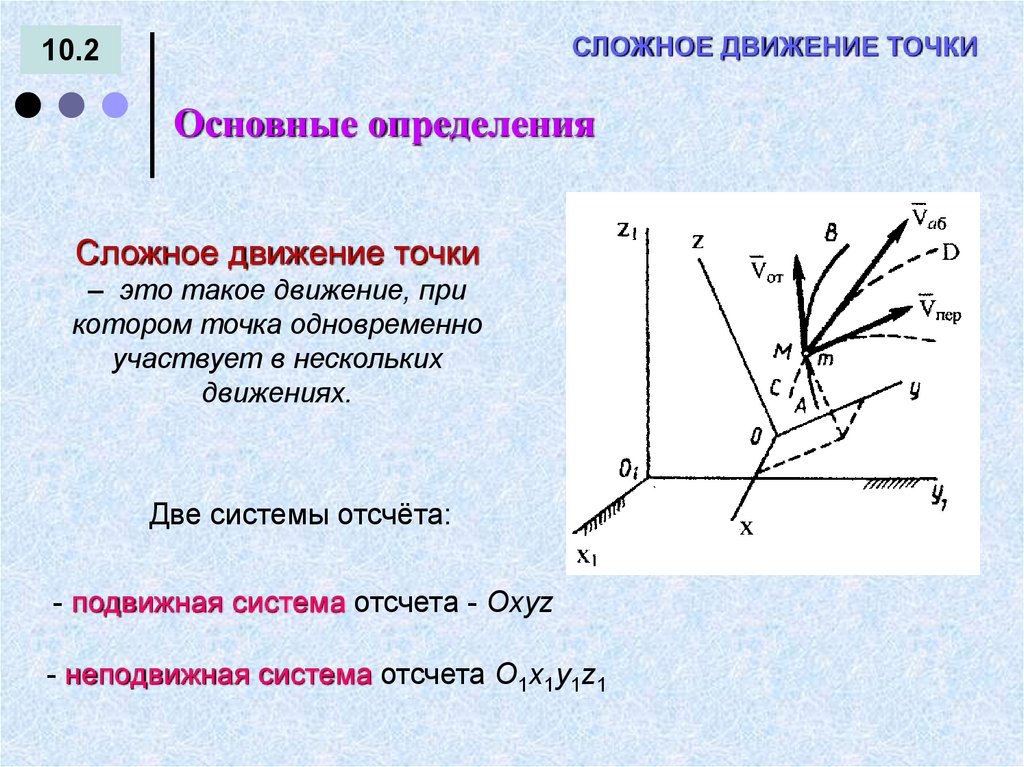
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
10.2
Основные определения
Сложное движение точки
– это такое движение, при
котором точка одновременно
участвует в нескольких
движениях.
Две системы отсчёта:
- подвижная система отсчета - Охуz
- неподвижная система отсчета О1х1у1z1

13.

СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
10.3
Основные определения
Относительное движение - движение
точки по отношению к подвижной
системе отсчета
vот
aот
Переносное движение - движение,
совершаемое подвижной системой
отсчета по отношению к неподвижной
системе
vпер
aпер
Абсолютное движение - движение,
совершаемое точкой по отношению к
неподвижной системе отсчета

14.

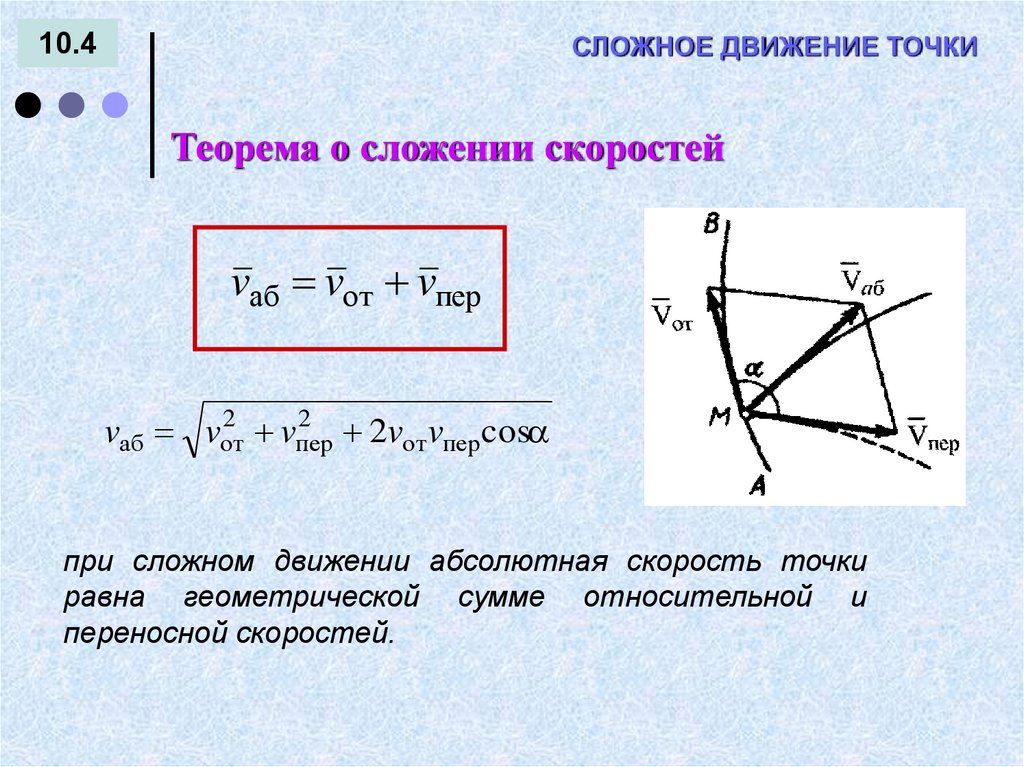
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
10.4
Теорема о сложении скоростей
vаб vот vпер
2
2
vаб vот
vпер
2vотvперcos
при сложном движении абсолютная скорость точки
равна геометрической сумме относительной и
переносной скоростей.

15.

СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
11.2
ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ
(ТЕОРЕМА КОРИОЛИСА)
dvаб dvот dvпер
aаб
dt
dt
dt
aаб
(dvот )от (dvот )пер (dvпер )от (dvпер )пер
dt
dt
dt
dt
aаб aот aпер aкор
акор
(dvпер )от
dt
(dvпер )пер
dt
- кориолисово ускорение
(ускорение Кориолиса)

16.

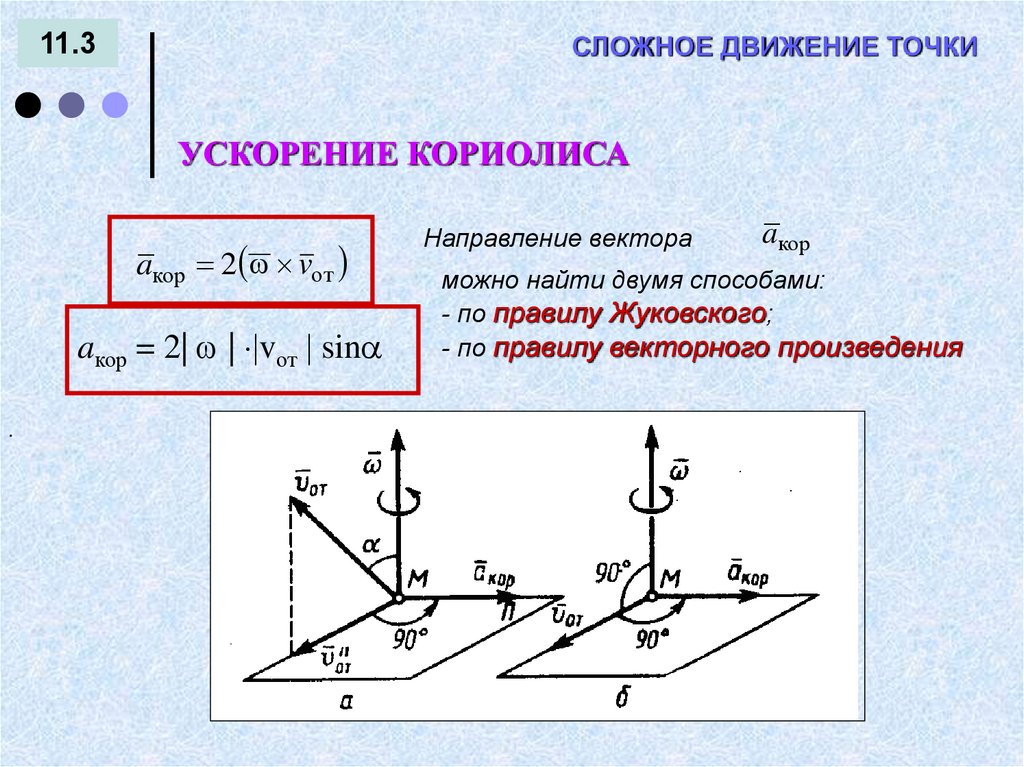
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
11.3
УСКОРЕНИЕ КОРИОЛИСА
aкор 2 vот
aкор = 2| | vот sin
.
Направление вектора
aкор
можно найти двумя способами:
- по правилу Жуковского;
- по правилу векторного произведения

17.

СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
11.4
УСКОРЕНИЕ КОРИОЛИСА
aкор 0
aкор 2 vот
в следующих случаях:
- когда = 0, т. е. переносное движение является поступательным;
- когда относительная скорость в данный момент времени
обращается в нуль;
- когда угол между векторами
когда
и
vот = 0, или = 180°, т.е.
vот параллелен оси переносного вращения

18.

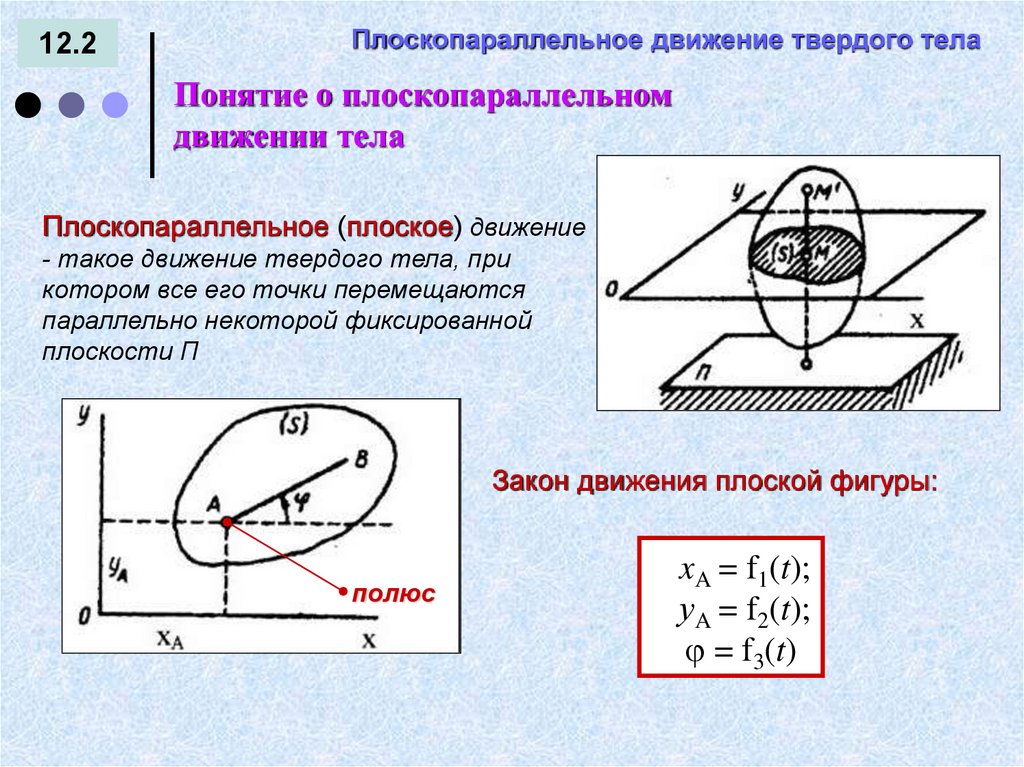
12.2
Плоскопараллельное движение твердого тела
Понятие о плоскопараллельном
движении тела
Плоскопараллельное (плоское) движение
- такое движение твердого тела, при
котором все его точки перемещаются
параллельно некоторой фиксированной
плоскости П
Закон движения плоской фигуры:
полюс
xA = f1(t);
уA = f2(t);
= f3(t)

19.

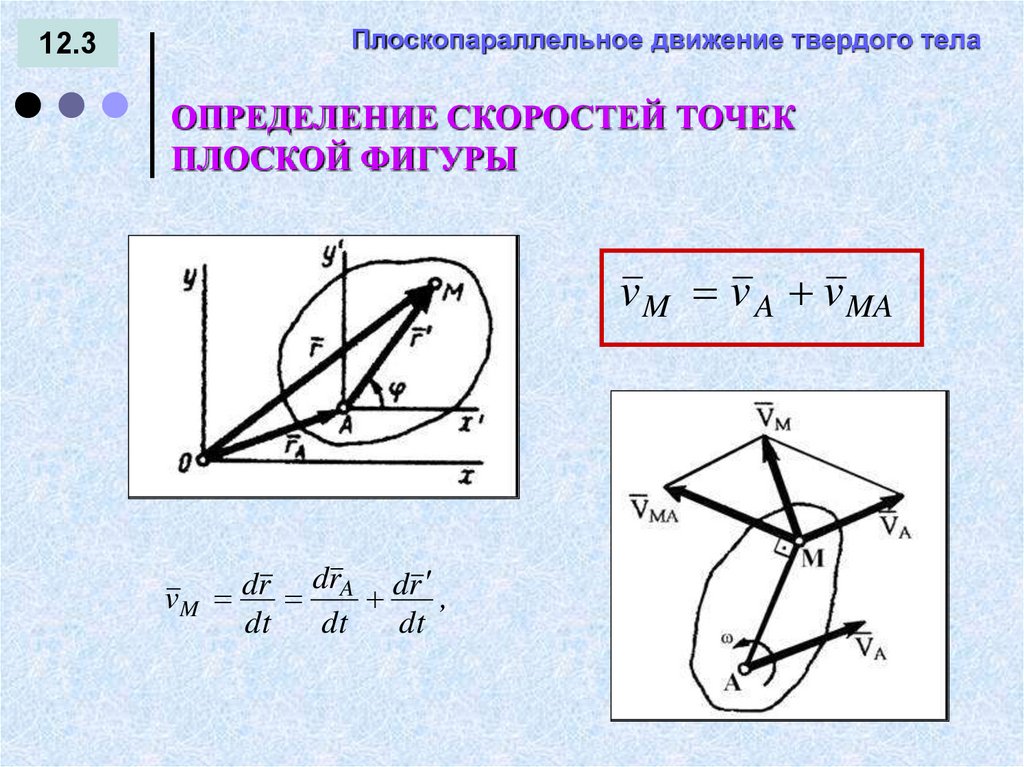
12.3
Плоскопараллельное движение твердого тела
ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК
ПЛОСКОЙ ФИГУРЫ
v M v A v MA
dr
vM dr A dr ,
dt
dt
dt

20.

12.4
Плоскопараллельное движение твердого тела
ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ
ТОЧЕК ПЛОСКОЙ ФИГУРЫ
v B v A v BA
vB cos = vA cos .
Проекции скоростей точек плоской фигуры на прямую,
проходящую через эти точки, равны, между собой.

21.

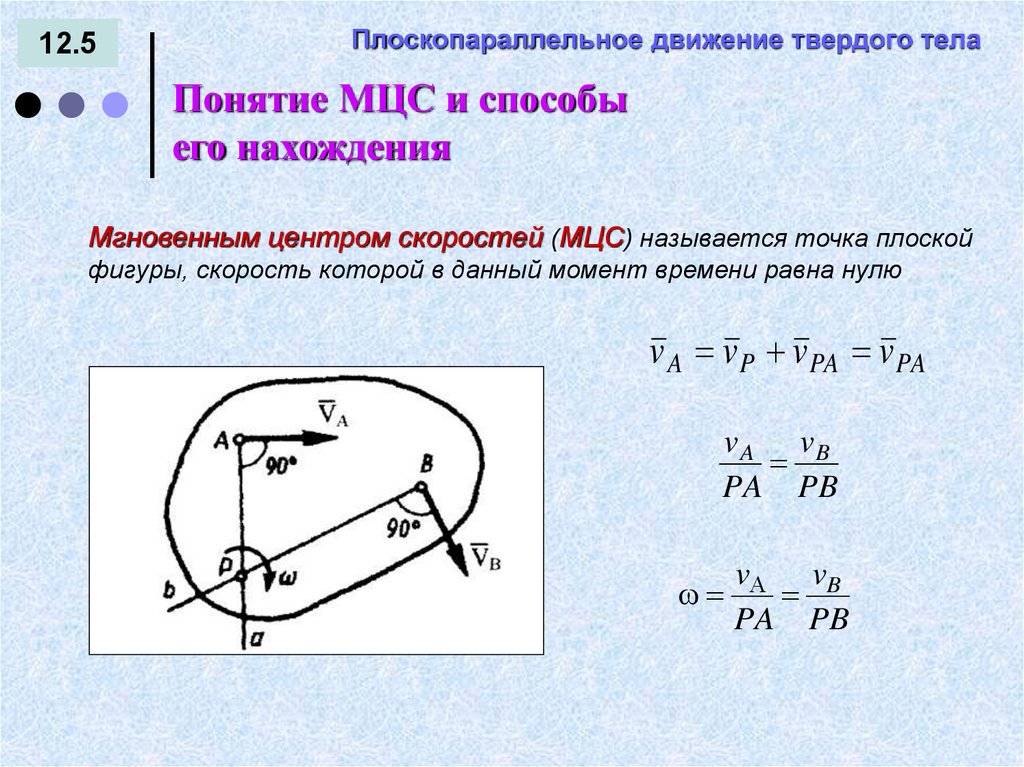
12.5
Плоскопараллельное движение твердого тела
Понятие МЦС и способы
его нахождения
Мгновенным центром скоростей (МЦС) называется точка плоской
фигуры, скорость которой в данный момент времени равна нулю
v A v P v PA v PA
v A vB
PA PB
vА vB
PA PB

22.

12.5
Плоскопараллельное движение твердого тела
Понятие МЦС и способы
его нахождения
Частные случаи определения мгновенного центра скоростей

23.

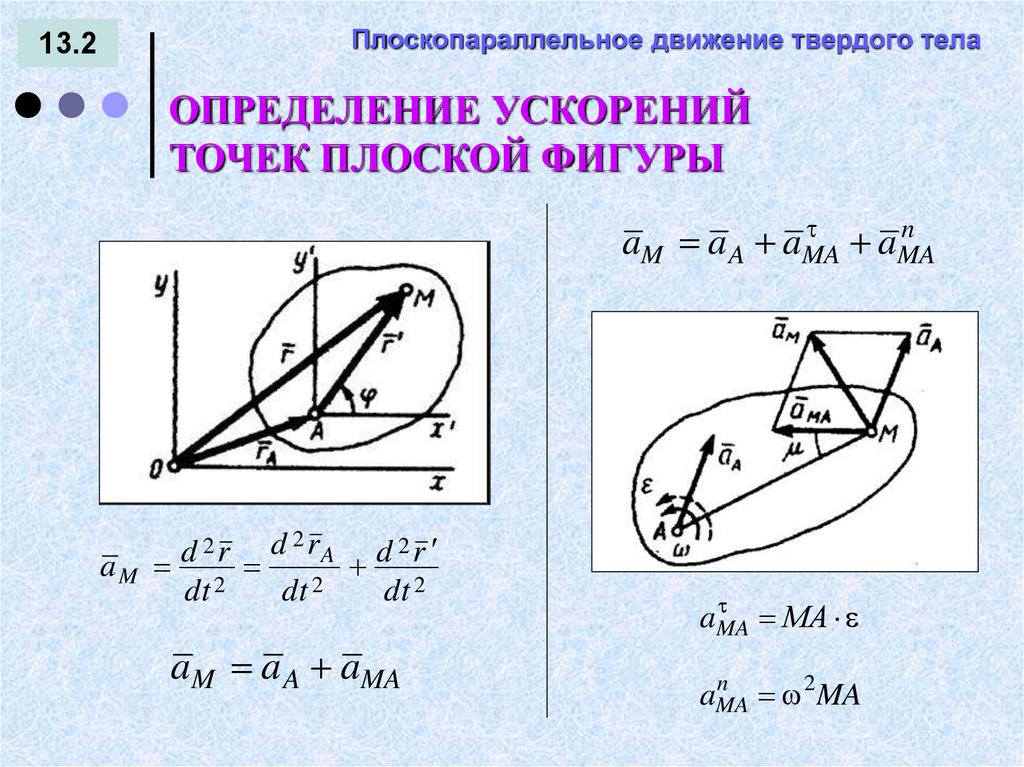
Плоскопараллельное движение твердого тела
13.2
ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ
ТОЧЕК ПЛОСКОЙ ФИГУРЫ
a a a
M
A
aM
aM
2r
d 2 rA d 2 r
d
2
2
dt
dt
dt 2
aM a A aMA
n
aM a A aMA
aMA
MA
a A aMA
n
aMA
aMA
МА
n
aMA
2 MA

24.

13.3
Плоскопараллельное движение твердого тела
МГНОВЕННЫЙ ЦЕНТР
УСКОРЕНИЙ
Точка, ускорение которой в данный момент времени равно
нулю называется мгновенным центром ускорений (МЦУ).
aM aQ aMQ aMQ
a M MQ 2 4
tgμ = ε/ω;

25.

Плоскопараллельное движение твердого тела
13.3
МГНОВЕННЫЙ ЦЕНТР
УСКОРЕНИЙ
a M MQ 2 4
tg μ = ε/ω;
Частные случаи :
- если =0, ω≠ 0, то угол
направлены к МЦУ;
=0
и ускорения всех точек будут
- если ≠0, ω = 0, то угол = 90о и ускорения всех точек
направлены перпендикулярно к отрезкам, соединяющим эти точки
с МЦУ