Similar presentations:
Основные формулы синуса и косинуса
1. Основные формулы для SINα и COSα
2. Цели урока
Прочитать п 7.4 стр 211 -212 до 3 теоремы3.
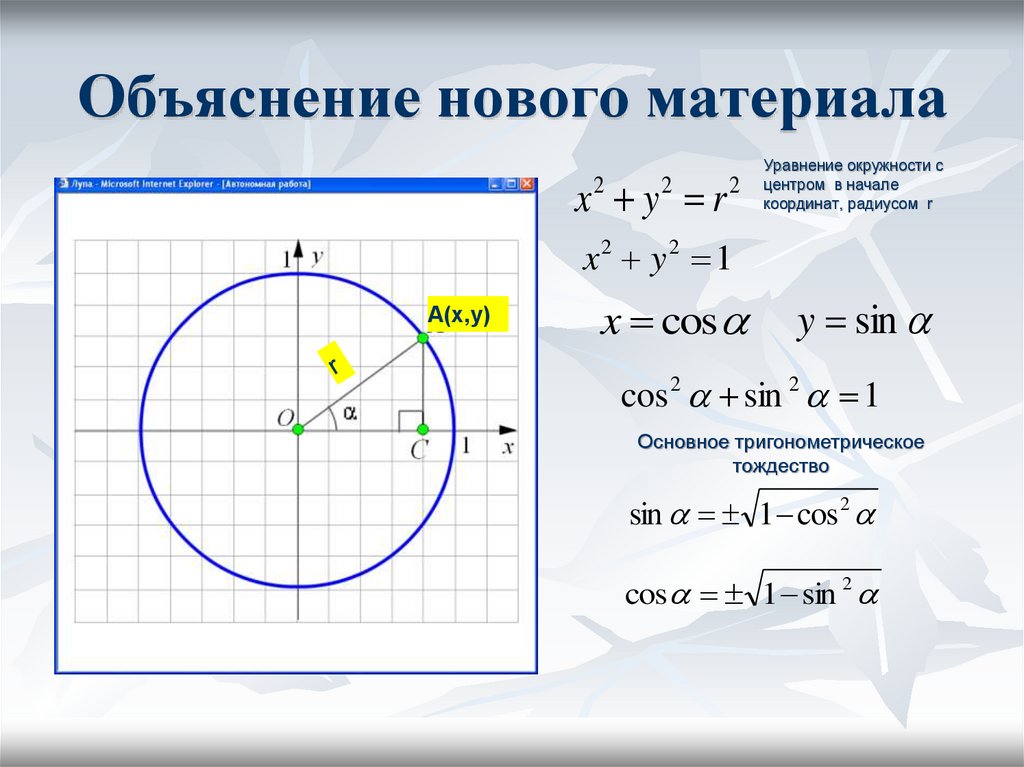
Объяснение нового материалаx2 y2 r 2
Уравнение окружности с
центром в начале
координат, радиусом r
x2 y 2 1
А(х,y)
x cos
y sin
cos 2 sin 2 1
Основное тригонометрическое
тождество
sin 1 cos 2
cos 1 sin 2
4. Объяснение нового материала
Теорема 1: Для любого угла α справедливоравенство cos 2 sin 2 1
Следствие: Для любого угла α справедливы неравенства
cos 1
sin 1
5. Следствие: Для любого угла α справедливы неравенства
Возможно ли равенство?Отвечаем да или нет
sin 1
cos 1
1
1
sin
2
2
cos
3
3
2 1
3
sin 2
3 1
4
cos 3
5
sin 1
6. Возможно ли равенство? Отвечаем да или нет
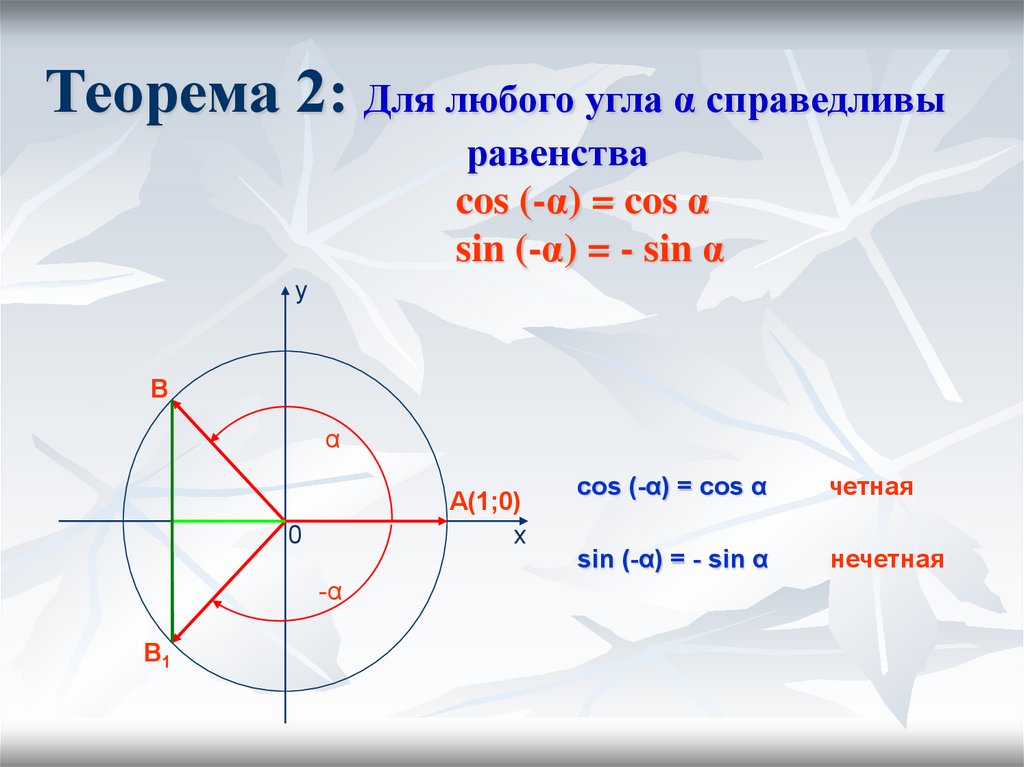
Теорема 2: Для любого угла α справедливыравенства
cos (-α) = cos α
sin (-α) = - sin α
y
В
α
A(1;0)
x
0
-α
В1
cos (-α) = cos α
четная
sin (-α) = - sin α
нечетная
7.
Укажите номера верныхравенств
1
sin( 3 x) sin 3 x
2
cos 5 x cos( 5 x)
3
sin( x
4
cos(
5
sin(
p
p
4
p
6
4
) sin(
) cos
p
4
p
4
) sin
x)
p
6
2
2
1
2
8. Укажите номера верных равенств
Как называются формулы,изученные на уроке ?
Выписываем формулы и рядом пишем названия
cos sin 1
2
2
sin 1, cos 1
cos cos
sin sin
9. Как называются формулы, изученные на уроке ?
Применение основноготригонометричекого тождества
№7.55(а)
Дано:
Найти:
Решение:
sin 0,8
p
2
p
cos α
cos 2 sin 2 1
cos 1 sin 2
cos 1 0,64 0,6
т.к. α – 2 четверть и cos α < 0, то cos α = - 0,6
Ответ:
cos α = - 0,6
10. Применение основного тригонометричекого тождества
sin1 cos
2
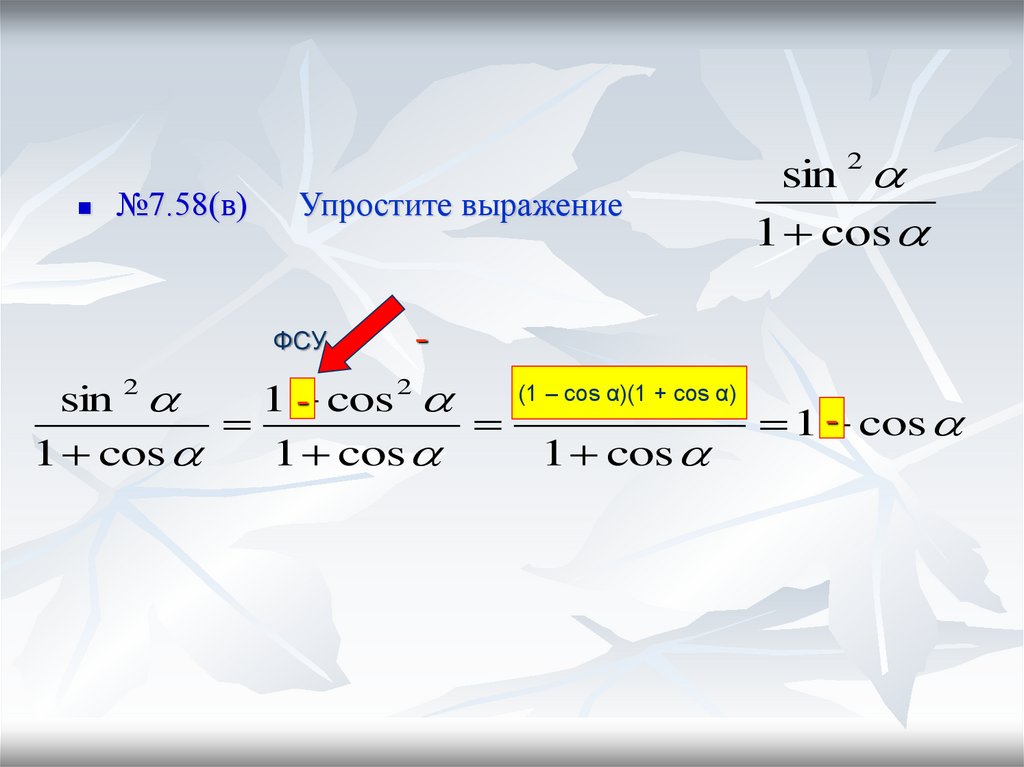
№7.58(в)
Упростите выражение
ФСУ
-
2
coscos
α)(1 +
cos)α)
sin 2
1
((11–
- cos 2
- cos
1
1 cos
1 cos
1 cos
11.
:«
Решение упражнений
№ 7.51 (а, в) используем основное тригонометрическое тождество
№ 7.52 (а, г, д) используем значение синуса или косинуса
№ 7.54 (а), № 7.57 (а, в), № 7.58 (а)
Самостоятельно
1 вычислите а) соs ( -45 0);
б) sin(-300) в)
12. Решение упражнений
Домашнее заданиеп. 7.4 стр. 214-215 (до теоремы 3)
№ 7.51(б, г), № 7.56, № 7.58(б, г).










 mathematics
mathematics








