Similar presentations:
Симметрия. Повторение, 8 класс (пункт 48, стр 110)
1.
Повторение,8 класс (пункт 48, стр 110)
pptcloud.r
2.
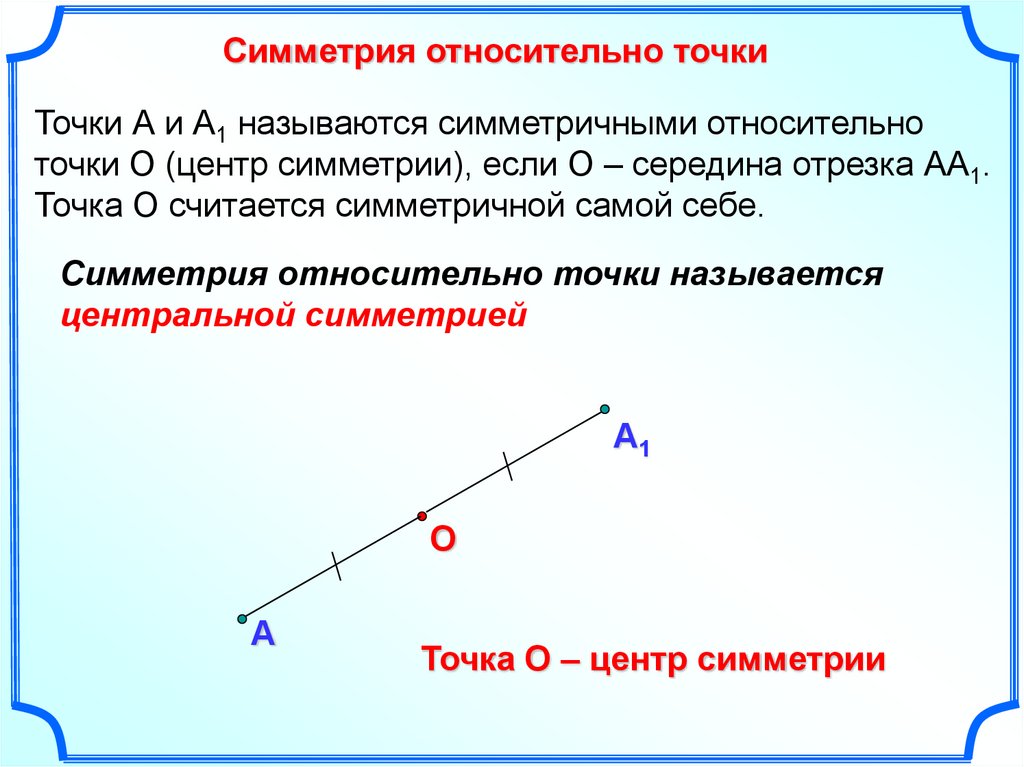
Симметрия относительно точкиТочки А и А1 называются симметричными относительно
точки О (центр симметрии), если О – середина отрезка АА1.
Точка О считается симметричной самой себе.
Симметрия относительно точки называется
центральной симметрией
А1
О
А
Точка О – центр симметрии
3.
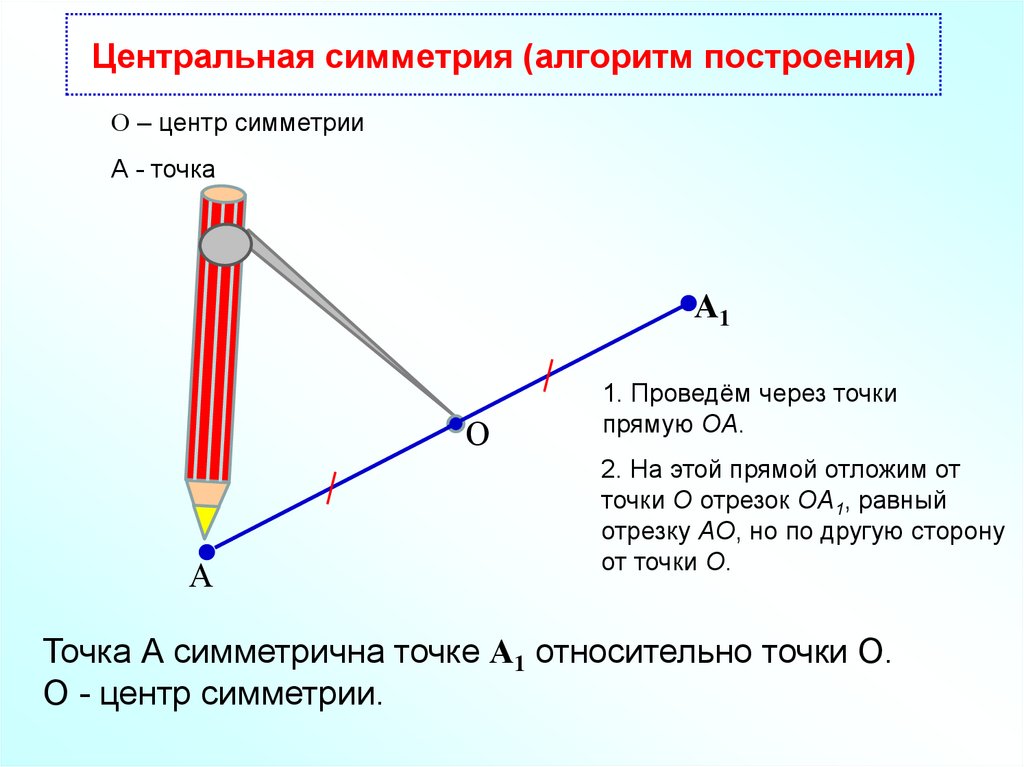
Центральная симметрия (алгоритм построения)О – центр симметрии
А - точка
А1
О
А
1. Проведём через точки
прямую OA.
2. На этой прямой отложим от
точки O отрезок OA1, равный
отрезку AO, но по другую сторону
от точки O.
Точка А симметрична точке А1 относительно точки О.
О - центр симметрии.
4.
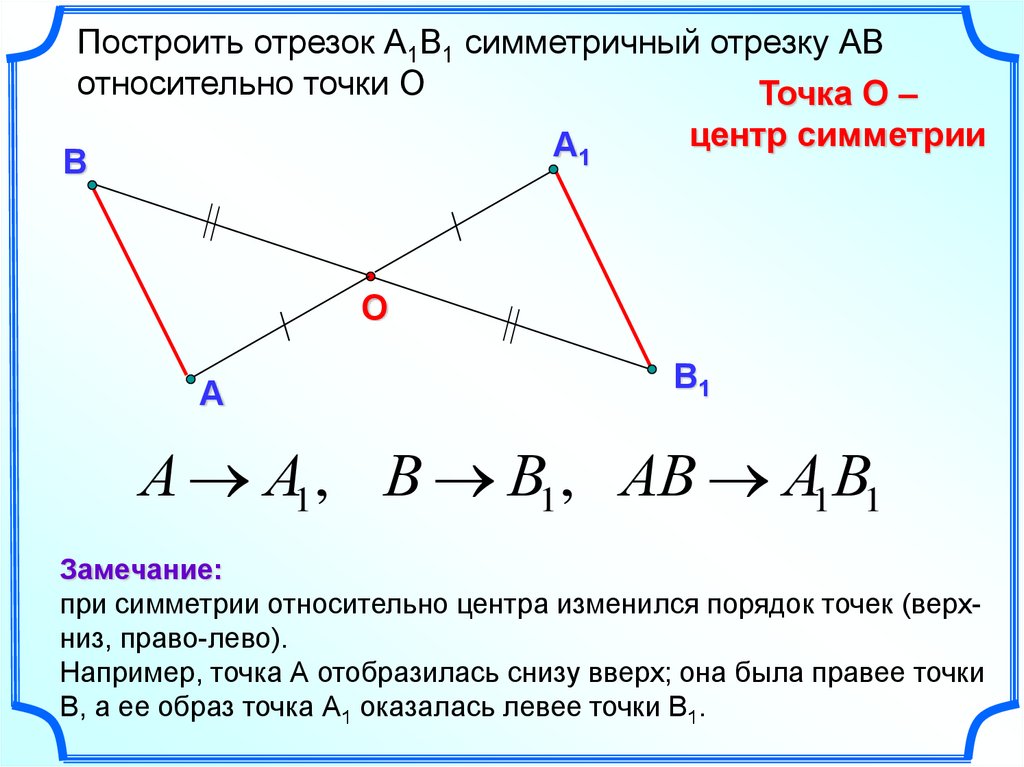
Построить отрезок А1В1 симметричный отрезку АВотносительно точки О
Точка О –
центр симметрии
А
1
В
О
А
В1
А А1 , В В1 , АВ А1В1
Замечание:
при симметрии относительно центра изменился порядок точек (верхниз, право-лево).
Например, точка А отобразилась снизу вверх; она была правее точки
В, а ее образ точка А1 оказалась левее точки В1.
5.
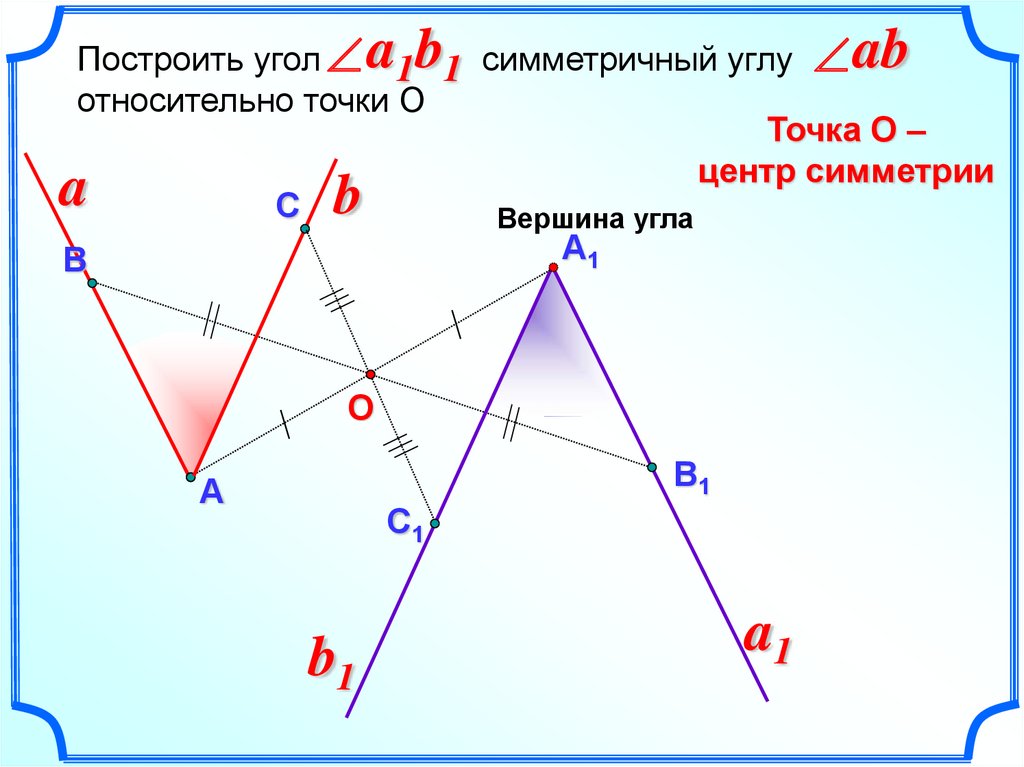
Построить угол 1 1 симметричный углуотносительно точки О
Точка О –
центр симметрии
C
Вершина угла
А1
В
ab
a
ab
b
О
В1
А
C1
b1
a1
6.
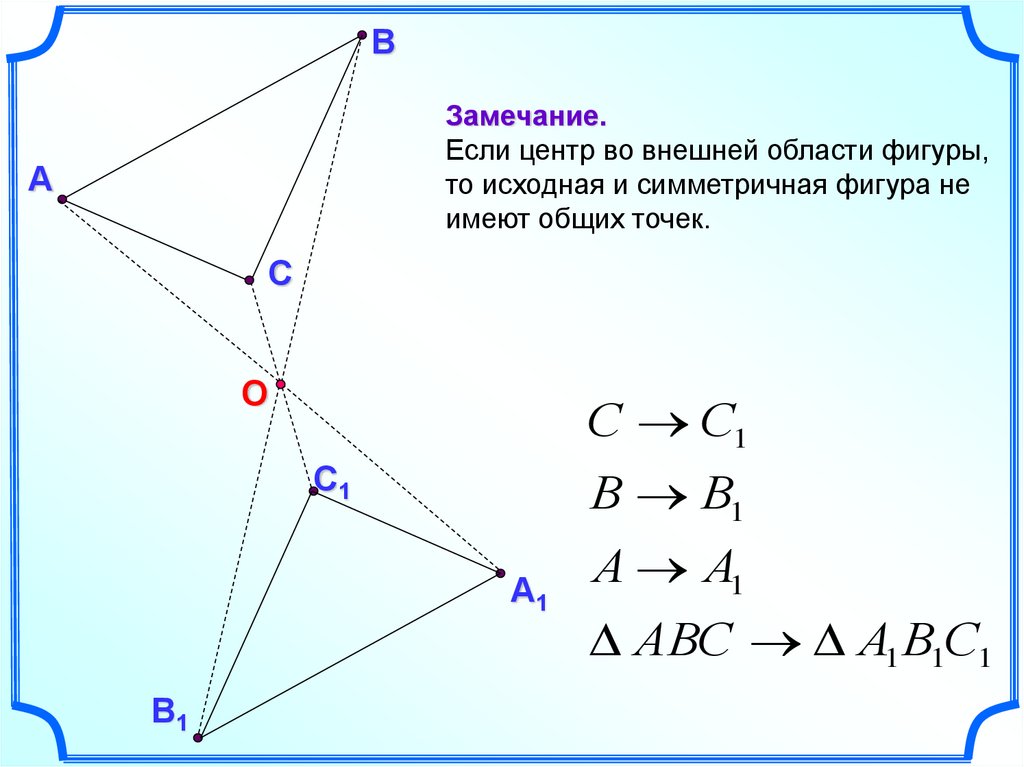
ВЗамечание.
Если центр во внешней области фигуры,
то исходная и симметричная фигура не
имеют общих точек.
А
С
О
С С1
С1
В В1
А1
В1
А А1
АВС А1 В1С1
7.
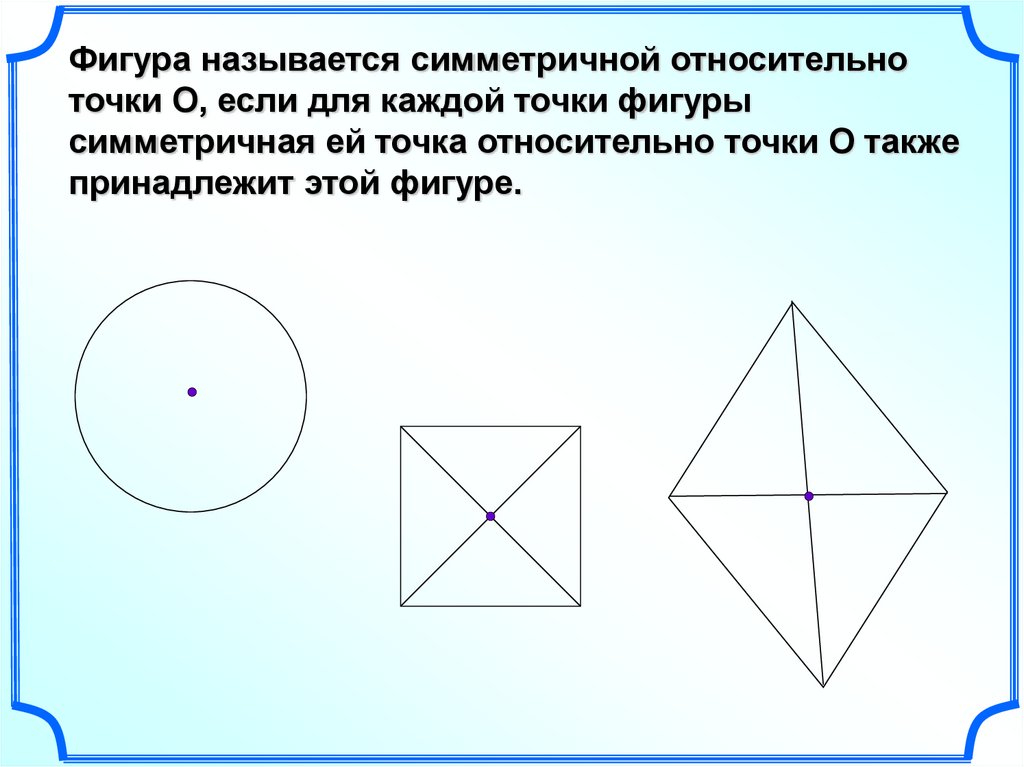
Фигура называется симметричной относительноточки О, если для каждой точки фигуры
симметричная ей точка относительно точки О также
принадлежит этой фигуре.
8.
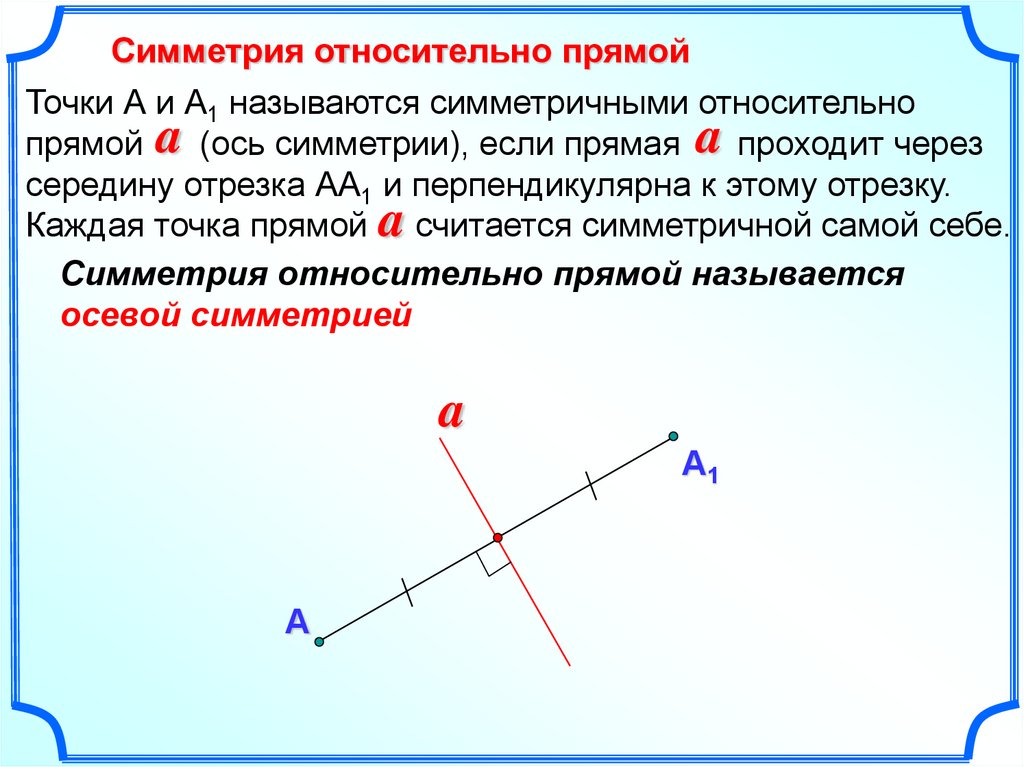
Симметрия относительно прямойТочки А и А1 называются симметричными относительно
прямой a (ось симметрии), если прямая a проходит через
середину отрезка АА1 и перпендикулярна к этому отрезку.
Каждая точка прямой a считается симметричной самой себе.
Симметрия относительно прямой называется
осевой симметрией
a
А1
А
9.
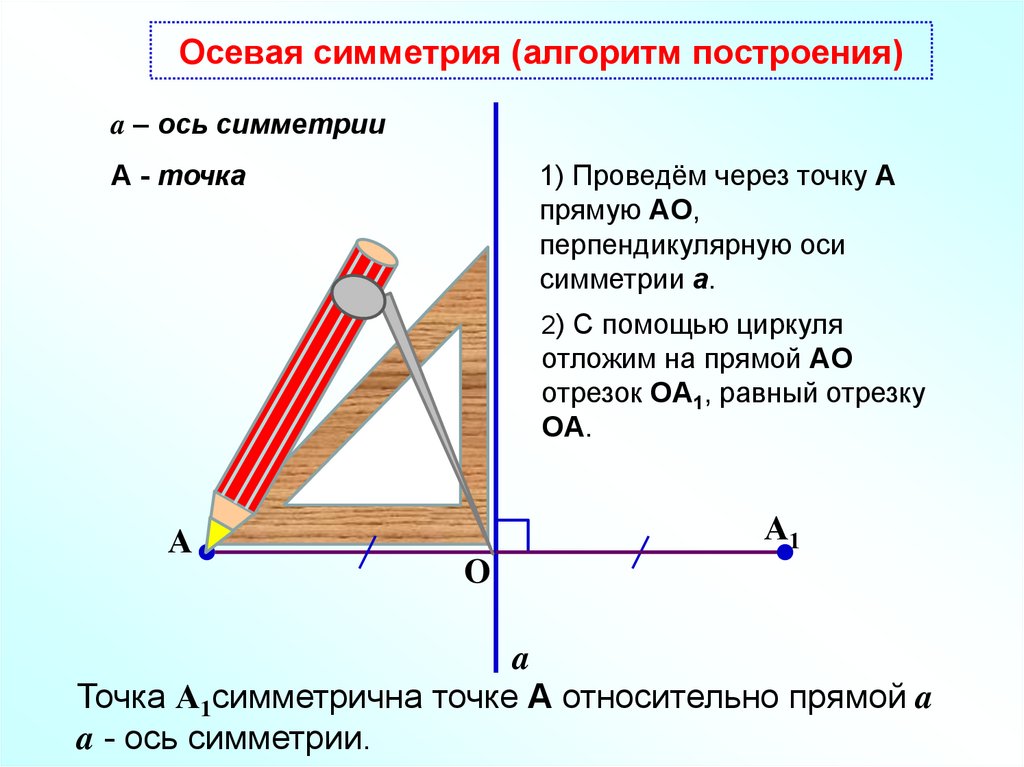
Осевая симметрия (алгоритм построения)a – ось симметрии
А - точка
1) Проведём через точку А
прямую АO,
перпендикулярную оси
симметрии a.
2) С помощью циркуля
отложим на прямой АO
отрезок OА1, равный отрезку
OА.
А
А1
O
a
Точка А1симметрична точке А относительно прямой a
a - ось симметрии.
10.
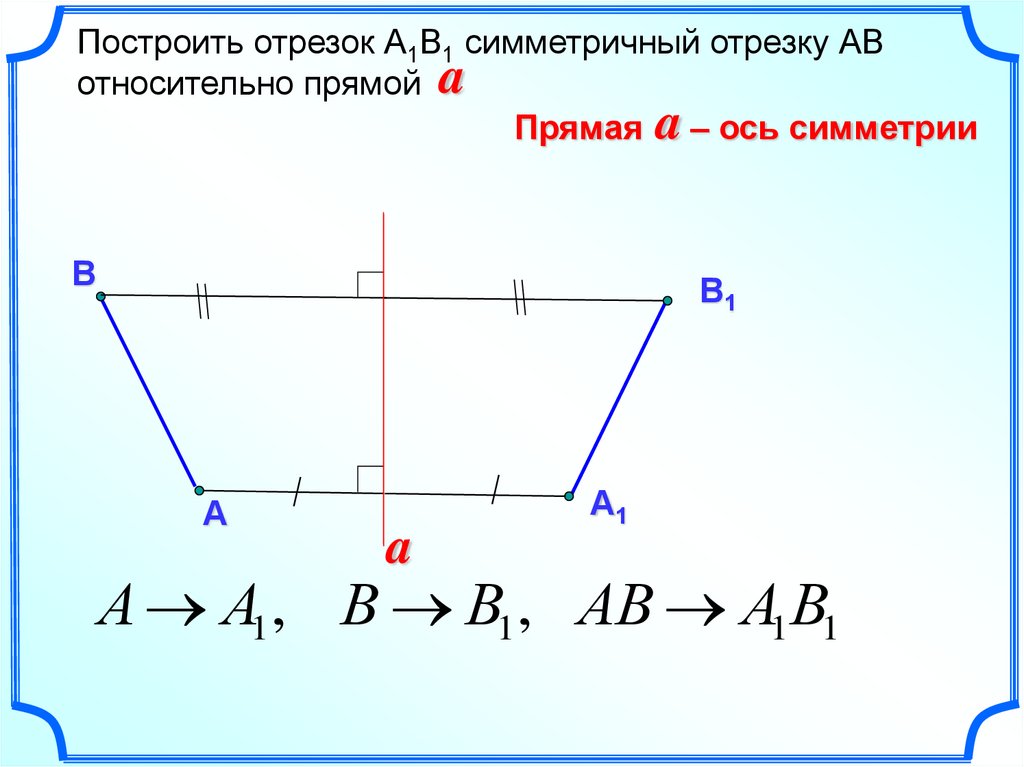
Построить отрезок А1В1 симметричный отрезку АВотносительно прямой a
Прямая a – ось симметрии
В
В1
А
a
А1
А А1 , В В1 , АВ А1В1
11.
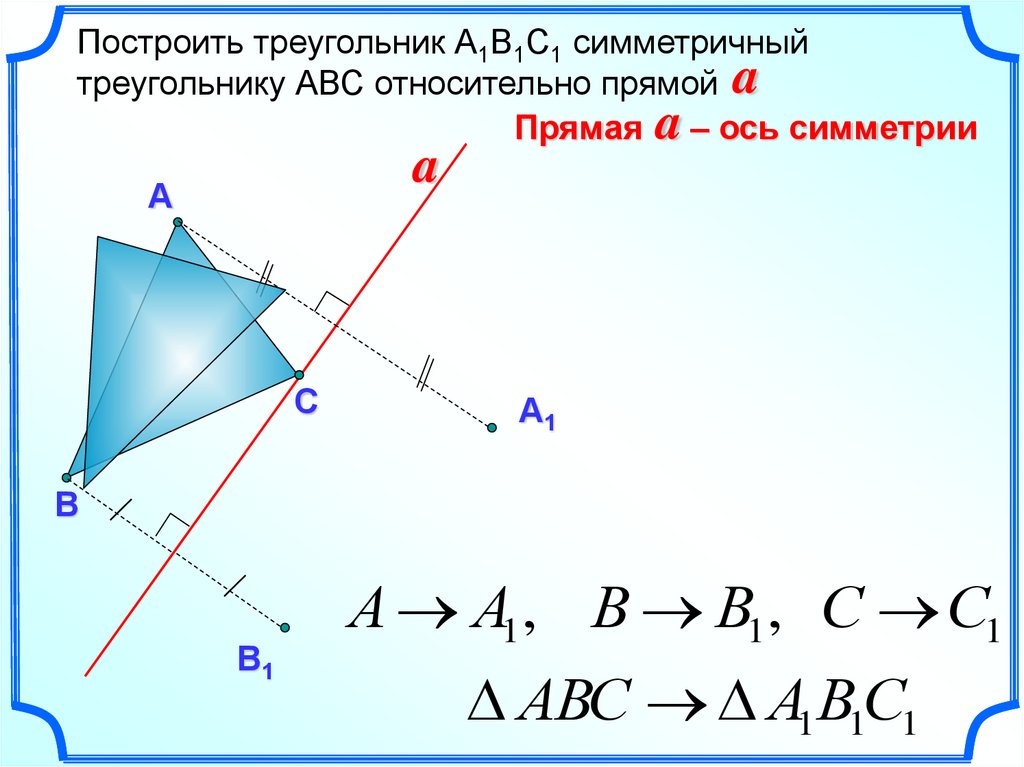
Построить треугольник А1В1С1 симметричныйтреугольнику АВС относительно прямой a
Прямая a – ось симметрии
a
А
С
А1
В
В1
А А1, В В1, С С1
АВС А1В1С1
12.
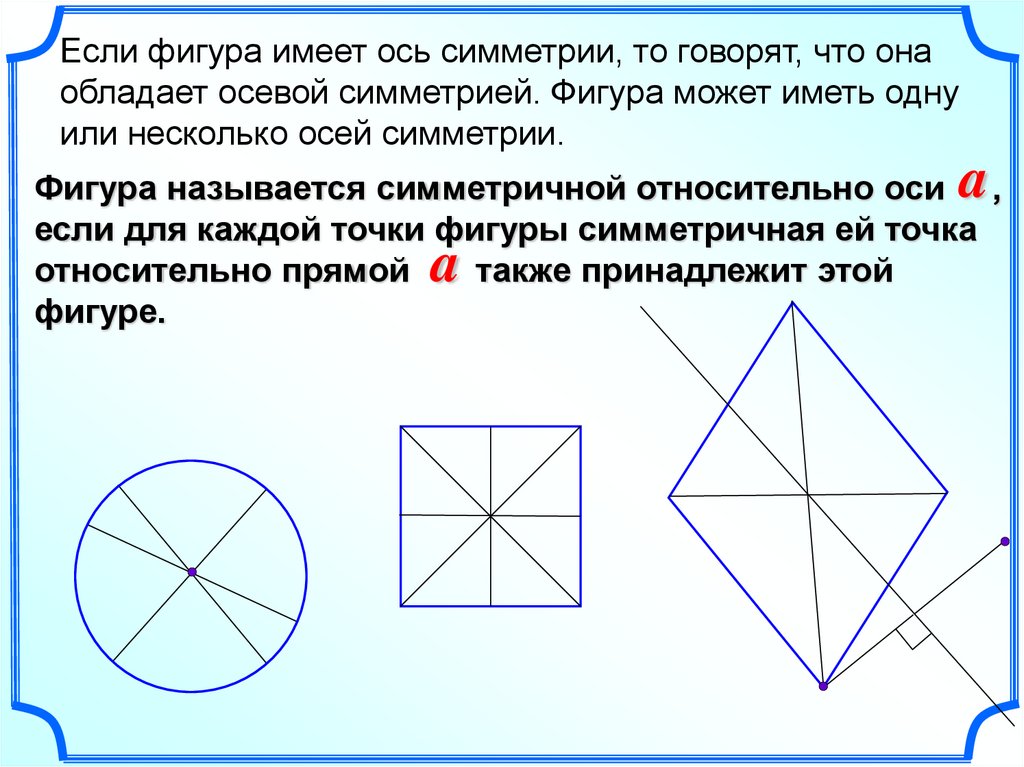
Если фигура имеет ось симметрии, то говорят, что онаобладает осевой симметрией. Фигура может иметь одну
или несколько осей симметрии.
a
Фигура называется симметричной относительно оси ,
если для каждой точки фигуры симметричная ей точка
относительно прямой
также принадлежит этой
фигуре.
a
13.
Домашнее задание1. В тетради выполнить чертежи со
слайдов 3, 4, 5, 6, 9,10, 11


 mathematics
mathematics








