Движение и виды движения

1. ДВИЖЕНИЕ И ВИДЫ ДВИЖЕНИЯ

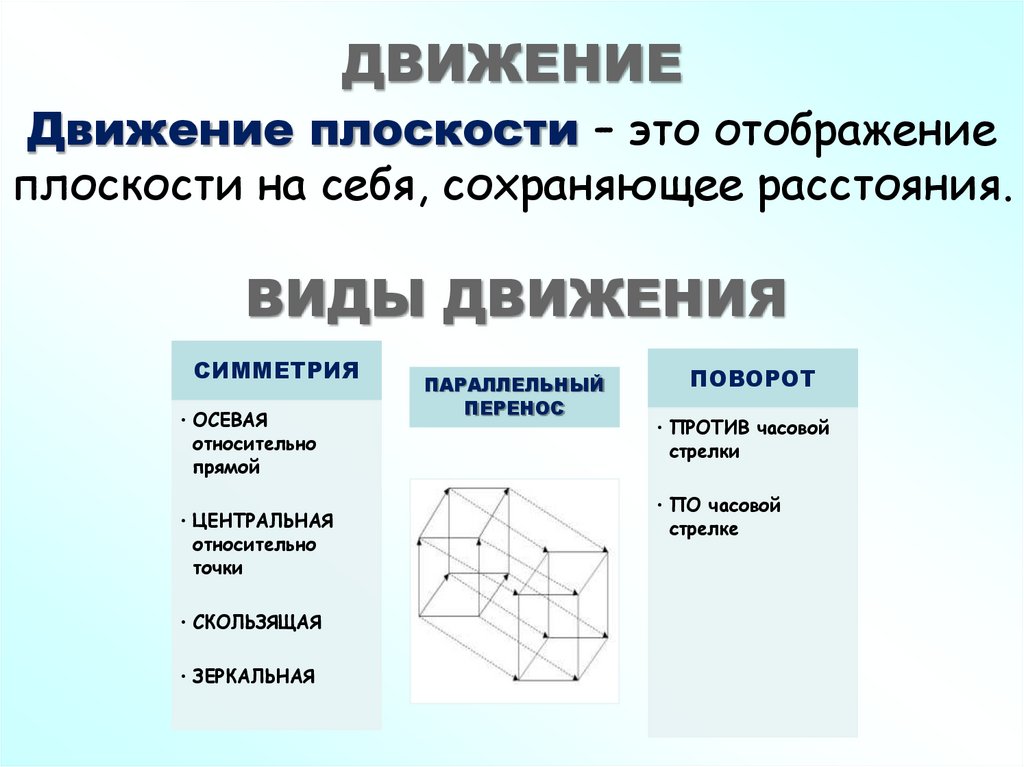
ДВИЖЕНИЕ

2. Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.

ДВИЖЕНИЕ
Движение плоскости – это отображение
плоскости на себя, сохраняющее расстояния.
ВИДЫ ДВИЖЕНИЯ
СИММЕТРИЯ
• ОСЕВАЯ
относительно
прямой
• ЦЕНТРАЛЬНАЯ
относительно
точки
• СКОЛЬЗЯЩАЯ
• ЗЕРКАЛЬНАЯ
ПАРАЛЛЕЛЬНЫЙ
ПЕРЕНОС
ПОВОРОТ
• ПРОТИВ часовой
стрелки
• ПО часовой
стрелке

3. ИСТОРИЯ СИММЕТРИИ

Ещё древние греки считали, что симметрия – это
гармония, соразмерность, они же и ввели термин,
который перешёл в русское слово «симметрия».
Как люди дошли до такой сложной и одновременно
такой простой вещи, как симметрия?
У древних народов, таких как шумеры и египтяне, у
первобытных племён, да и в наше время симметрия
ассоциируется не только с красотой и гармонией, но и
прежде всего с магией. Не зря же люди в эпоху
мегалита для ритуальных целей сооружали кромлихи в
форме круга – «идеально симметричной»
геометрической фигуры.

4.

ЗНАЕТЕ ЛИ ВЫ, ЧТО…
Слово симмет рия в переводе с
древнегреческого языка –
это «соразмерность».
Под симметрией в широком
смысле этого слова понимают
всякую правильность во внутреннем
строении тела или фигуры.
Учение о различных видах симметрии
представляет большую и важную ветвь
геометрии, тесно связанную с отраслями
естествознания и техники, начиная с
текстильного производства и архитектурной мозаики,
а кончая тонкими вопросами строения вещества.

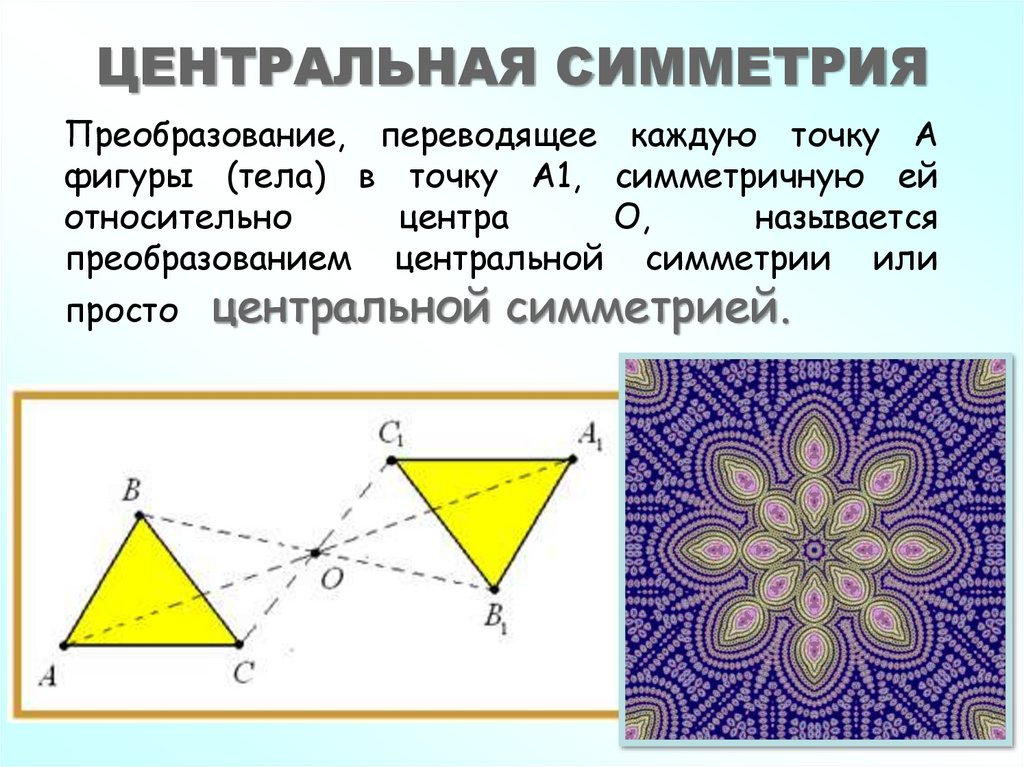
5. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ

Преобразование, переводящее каждую точку А
фигуры (тела) в точку А1, симметричную ей
относительно
центра
О,
называется
преобразованием центральной симметрии или
просто
центральной симметрией.

6.

7.

Симметрия относительно точки
Точки А и А1 называются симметричными относительно
точки О (центр симметрии), если О – середина отрезка АА1.
Точка О считается симметричной самой себе.
Симметрия относительно точки называется
центральной симметрией
А1
О
А
Точка О – центр симметрии

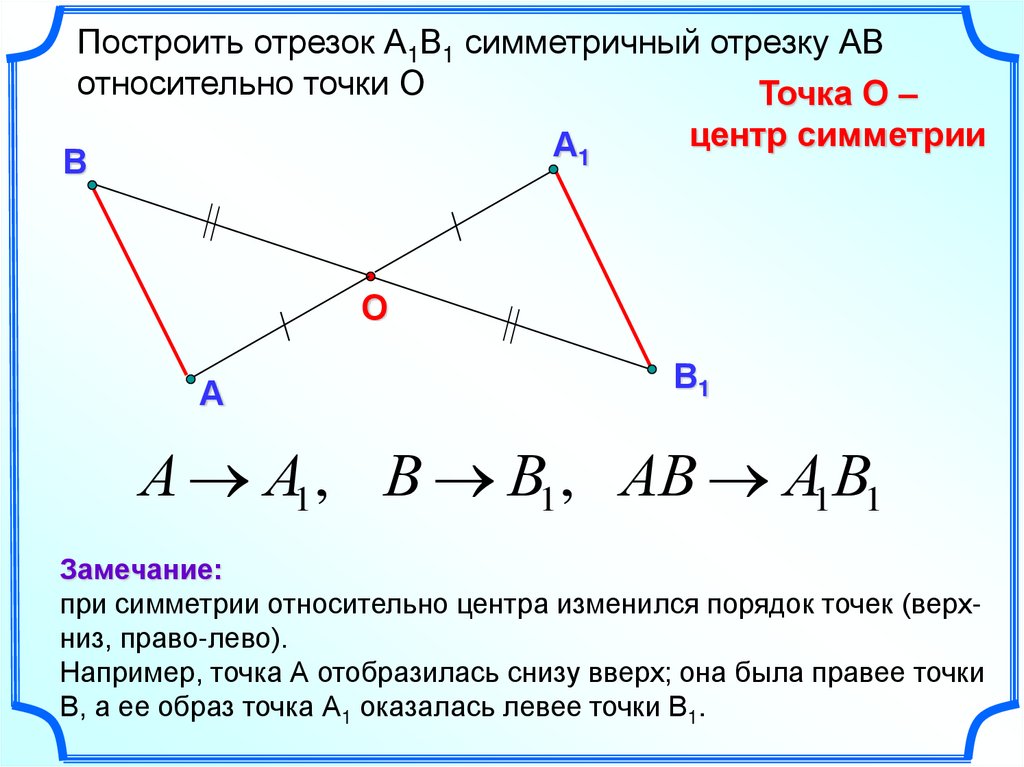
8.

Построить отрезок А1В1 симметричный отрезку АВ
относительно точки О
Точка О –
центр симметрии
А
1
В
О
А
В1
А А1 , В В1 , АВ А1В1
Замечание:
при симметрии относительно центра изменился порядок точек (верхниз, право-лево).
Например, точка А отобразилась снизу вверх; она была правее точки
В, а ее образ точка А1 оказалась левее точки В1.

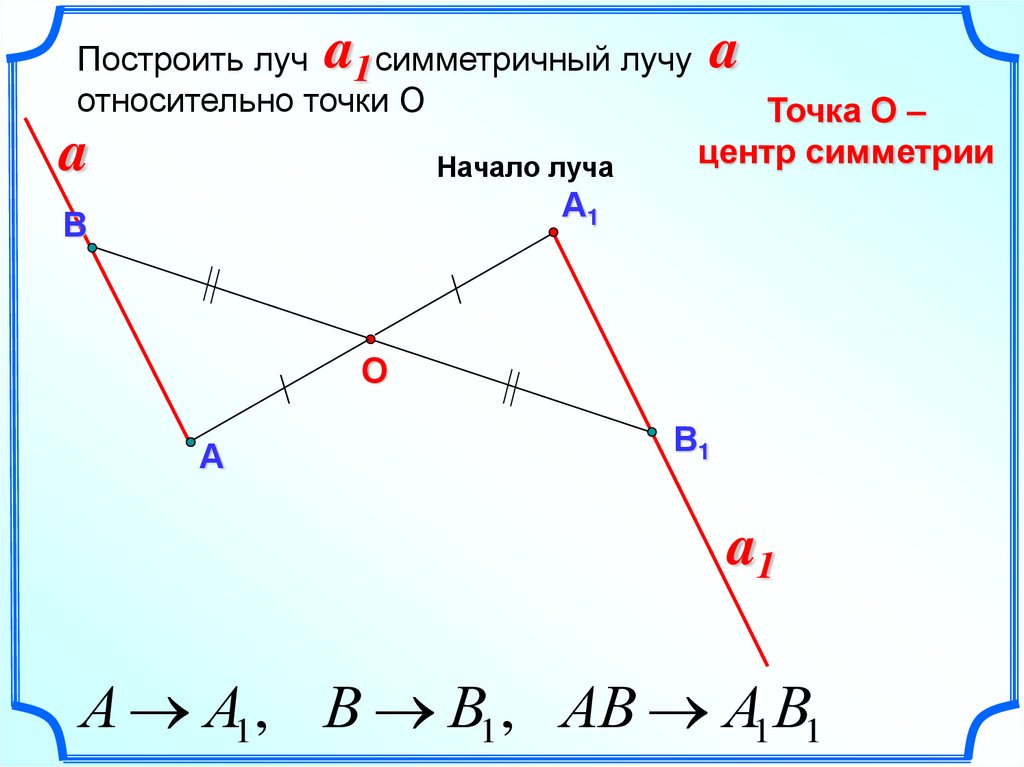
9.

a
Построить луч 1 симметричный лучу
относительно точки О
a
Начало луча
В
А1
a
Точка О –
центр симметрии
О
А
В1
a1
А А1 , В В1 , АВ А1В1

10.

b
a
Если центр симметрии
в начале луча, то при
симметрии луч отобразится на
…
О
О
b1
Если центр симметрии
принадлежит лучу, то при
симметрии …
a1

11.

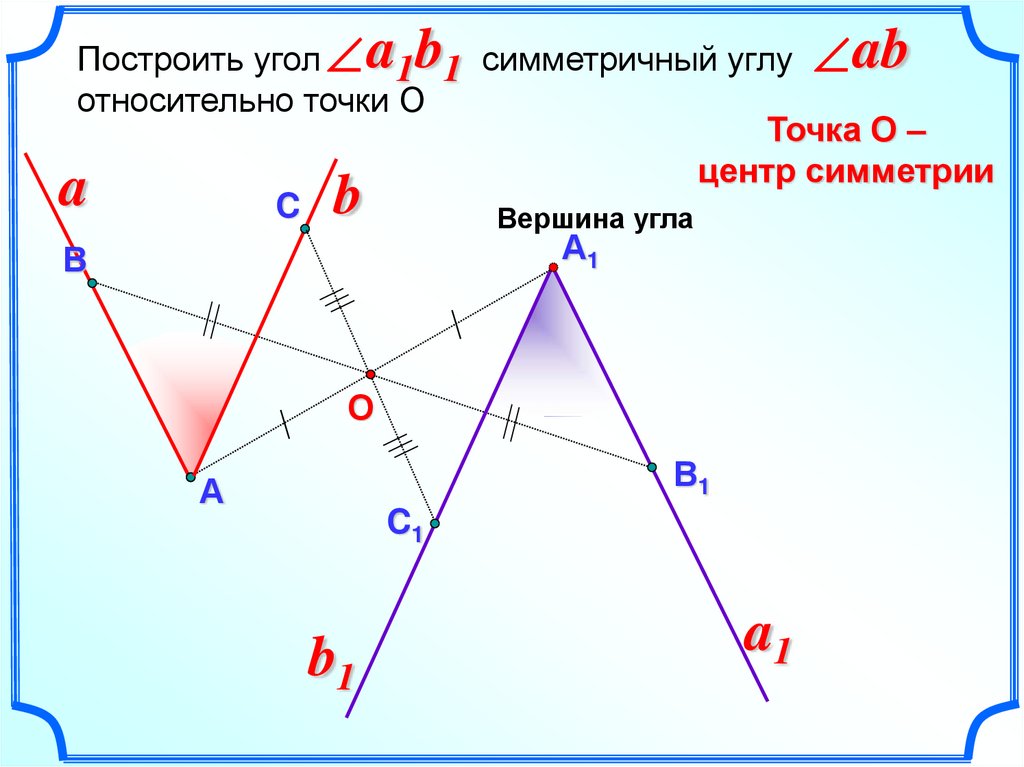
Построить угол 1 1 симметричный углу
относительно точки О
Точка О –
центр симметрии
C
Вершина угла
А1
В
ab
a
ab
b
О
В1
А
C1
b1
a1

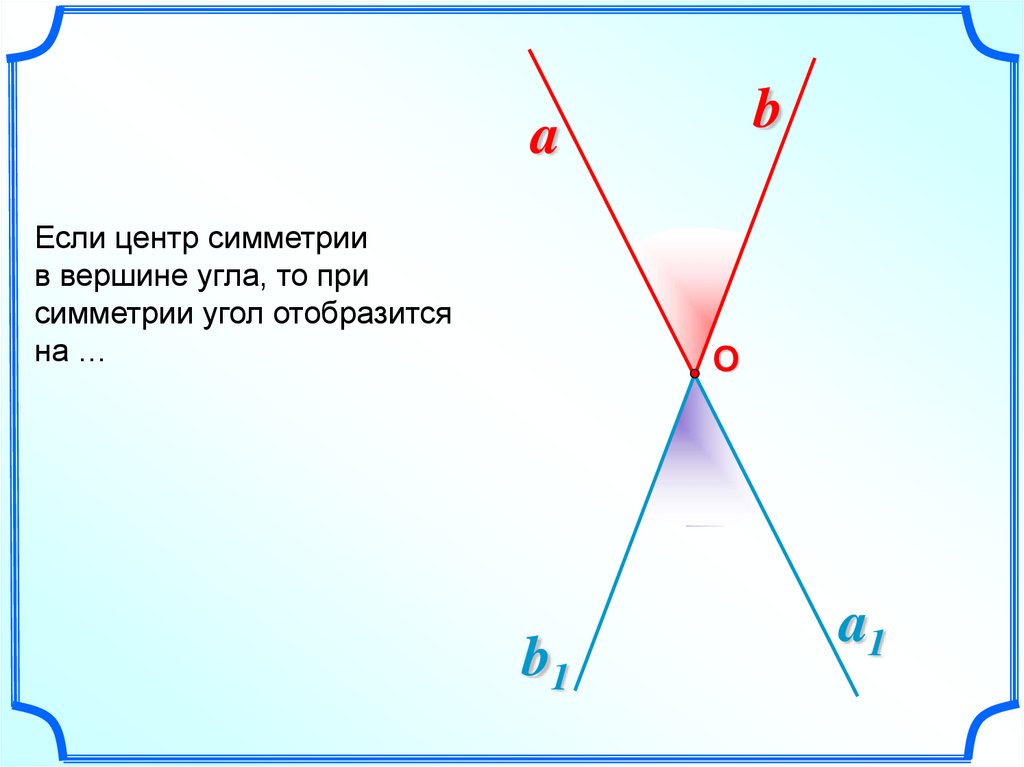
12.

b
a
Если центр симметрии
в вершине угла, то при
симметрии угол отобразится
на …
О
b1
a1

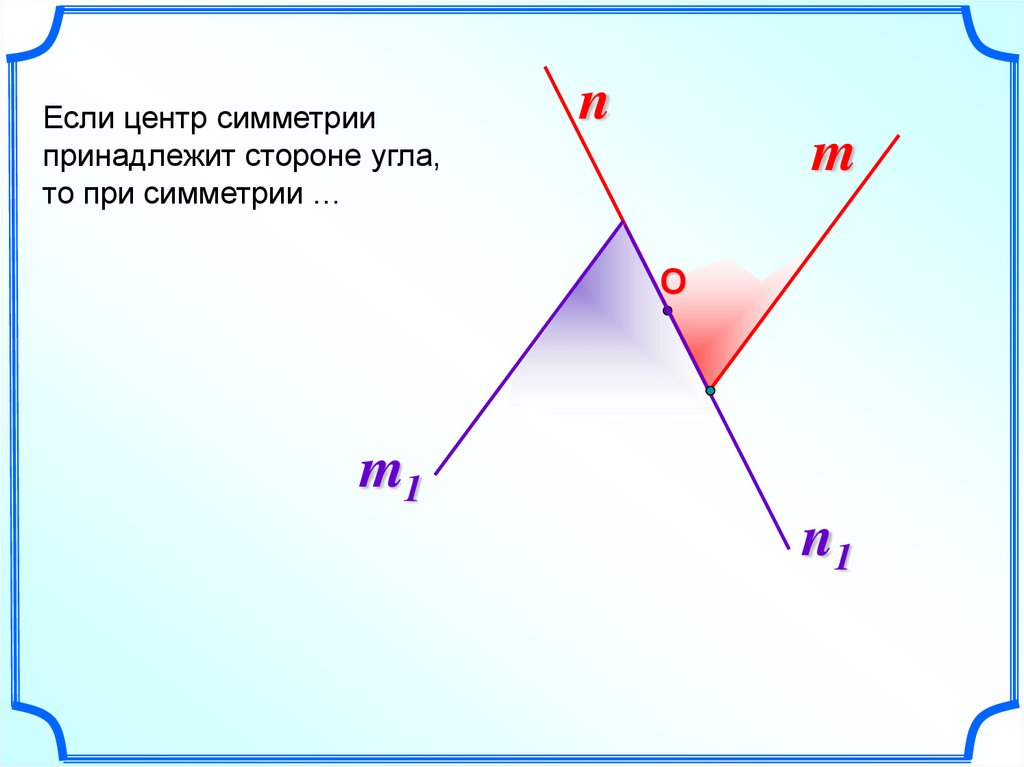
13.

Если центр симметрии
принадлежит стороне угла,
то при симметрии …
n
m
О
m1
n1

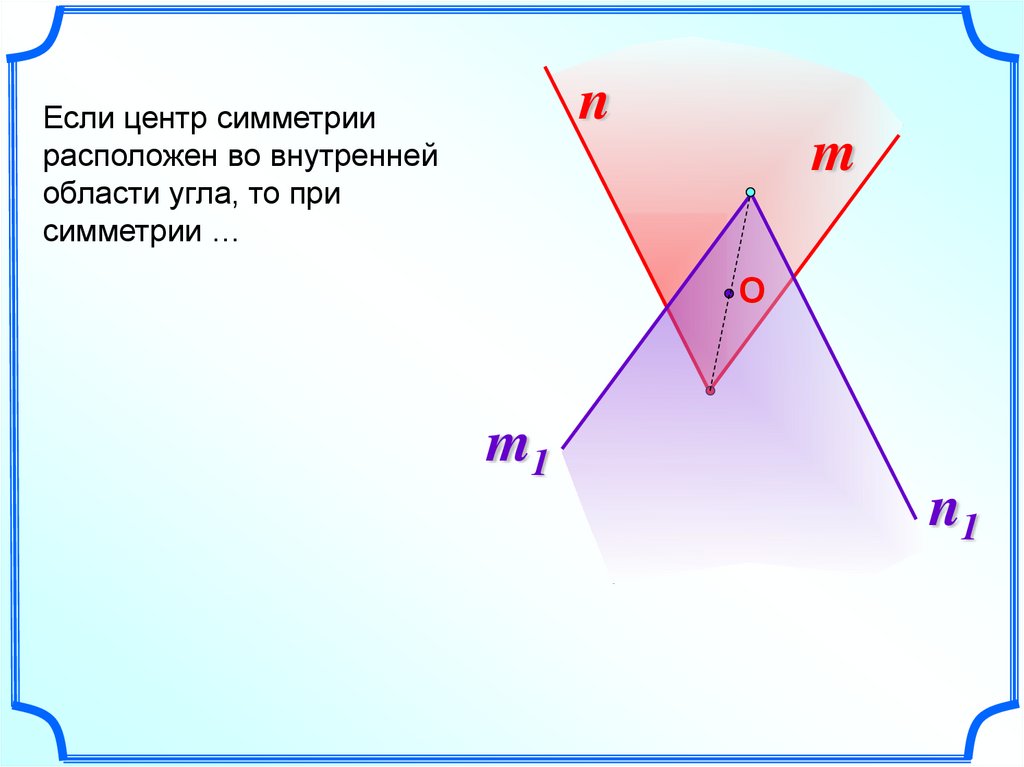
14.

n
Если центр симметрии
расположен во внутренней
области угла, то при
симметрии …
m
О
m1
n1

15.

В
Замечание.
Если центр во внешней области фигуры,
то исходная и симметричная фигура не
имеют общих точек.
А
С
О
С С1
С1
В В1
А1
В1
А А1
АВС А1 В1С1

16.

В
С1
Замечание.
Если центр во внутренней области
фигуры, то исходная и симметричная
фигура имеют общие точки
(6-угольник).
А
О
А1
С
В1
С С1
В В1
А А1
АВС А1 В1С1

17.

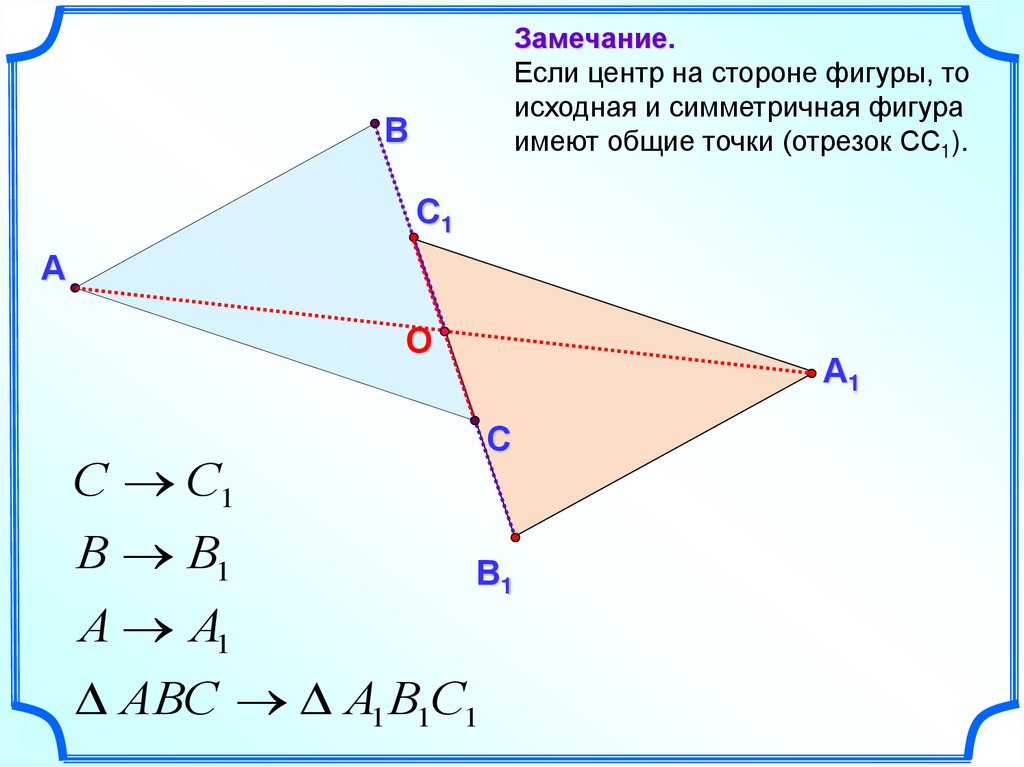
Замечание.
Если центр на стороне фигуры, то
исходная и симметричная фигура
имеют общие точки (отрезок СС1).
В
С1
А
О
А1
С
С С1
В В1
А А1
В1
АВС А1 В1С1

18.

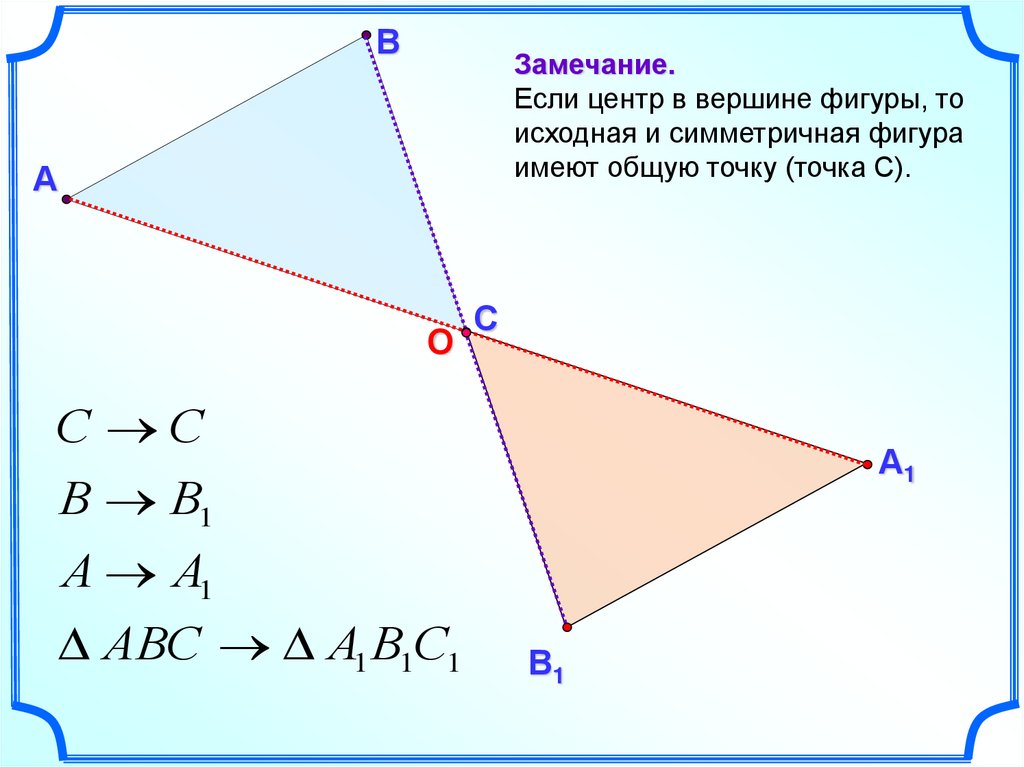
В
Замечание.
Если центр в вершине фигуры, то
исходная и симметричная фигура
имеют общую точку (точка С).
А
О
С
С С
В В1
А1
А А1
АВС А1 В1С1
В1

19.

20.

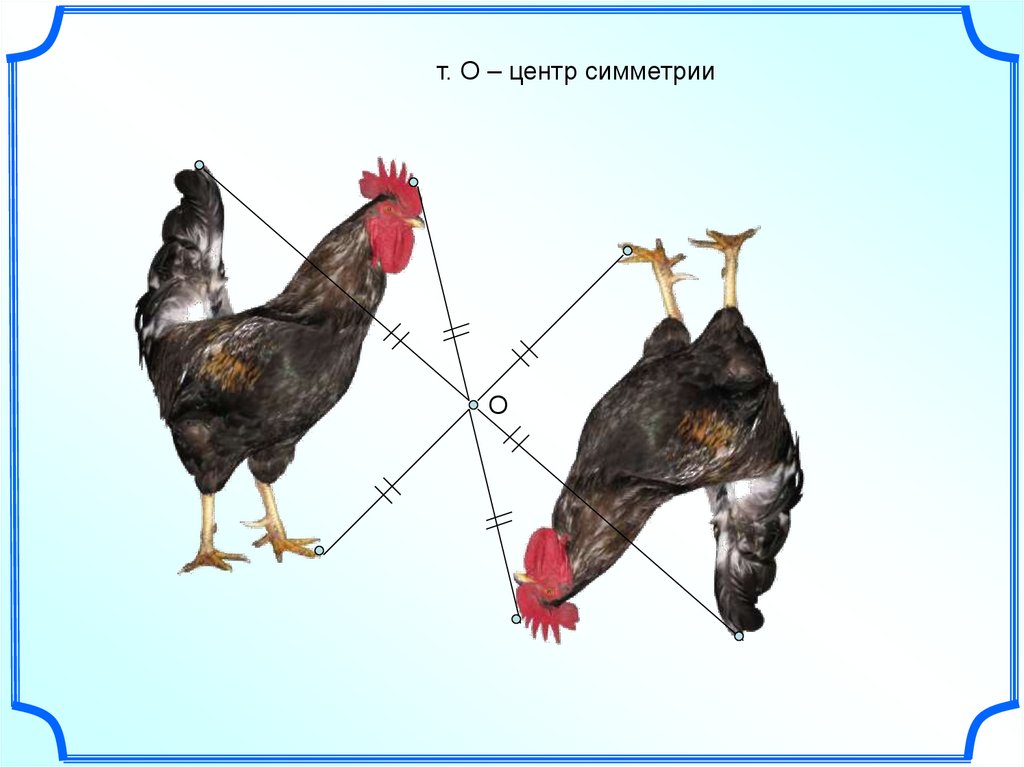
т. О – центр симметрии
О

21.

т. О – центр симметрии
A1
C
O
B1
B
A
C1

22.

Фигура называется симметричной относительно
точки О, если для каждой точки фигуры
симметричная ей точка относительно точки О также
принадлежит этой фигуре.

23.

Правильный треугольник
Правильный шестиугольник
Отрезок
Какая точка является центром симметрии фигур?
Параллелограмм
Прямоугольник

24.

Фигура называется симметричной относительно
точки О, если для каждой точки фигуры
симметричная ей точка относительно точки О также
принадлежит этой фигуре.
Какие буквы имеют центр симметрии?
О
S Z
Ф Х И

25.

Стоя перед чёрной доской и рисуя на ней мелом
разные фигуры, я вдруг был поражен мыслью: почему
симметрия приятна глазу? Что такое симметрия? Это
врождённое чувство, отвечал я себе. На чём оно
основано?
Л.Н.Толстой «Отрочество»

26.

http://www.point.ru/photo/galleries/12876/

27.

http://www.point.ru/photo/galleries/12876/

28.

http://www.point.ru/photo/galleries/12876/

29.

http://www.point.ru/photo/galleries/12876/

30.

http://www.point.ru/photo/galleries/12876/

31.

Хотите увидеть больше?
ВАМ СЮДА:
http://www.point.ru/photo/galleries/12876/

32.

Причудливые формы в природе
http://www.lookatme.ru/flows/illy
ustratsiya/posts/36694-ernsthaeckel
Обладает ли центральной
симметрией 5-угольник?

33.

Причудливые формы в природе
Хотите увидеть больше? ВАМ
СЮДА:
http://www.lookatme.ru/flows/illy
ustratsiya/posts/36694-ernsthaeckel

34.

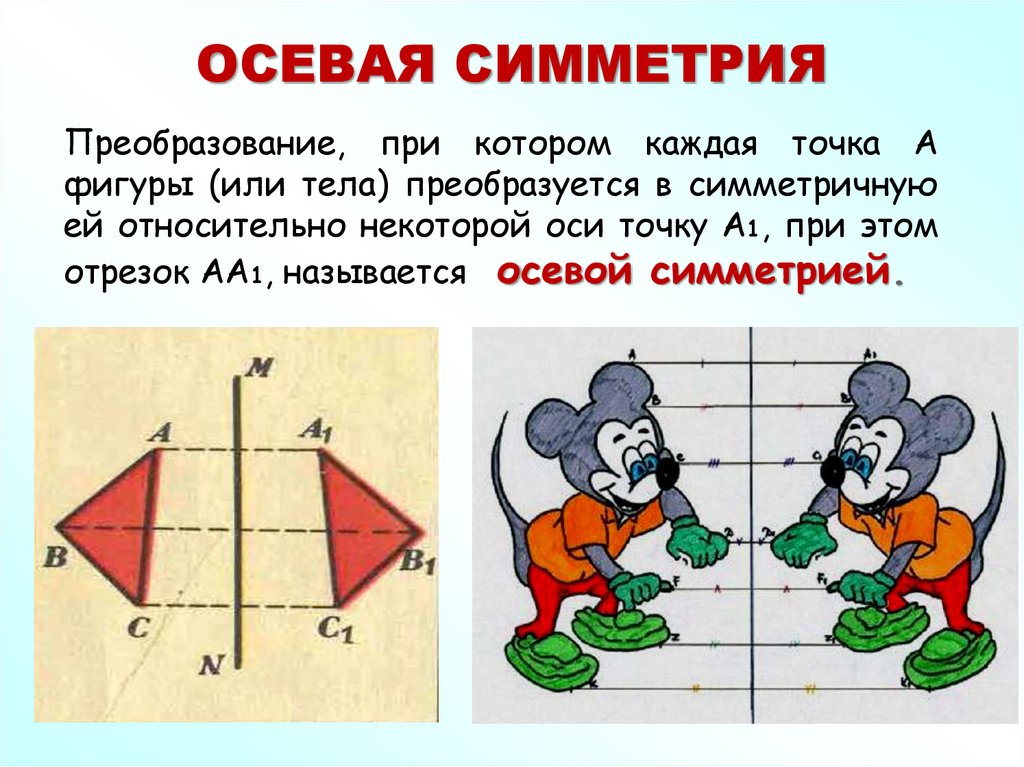
35. ОСЕВАЯ СИММЕТРИЯ

Преобразование, при котором каждая точка А
фигуры (или тела) преобразуется в симметричную
ей относительно некоторой оси точку А1, при этом
отрезок АА1, называется осевой симметрией.

36.

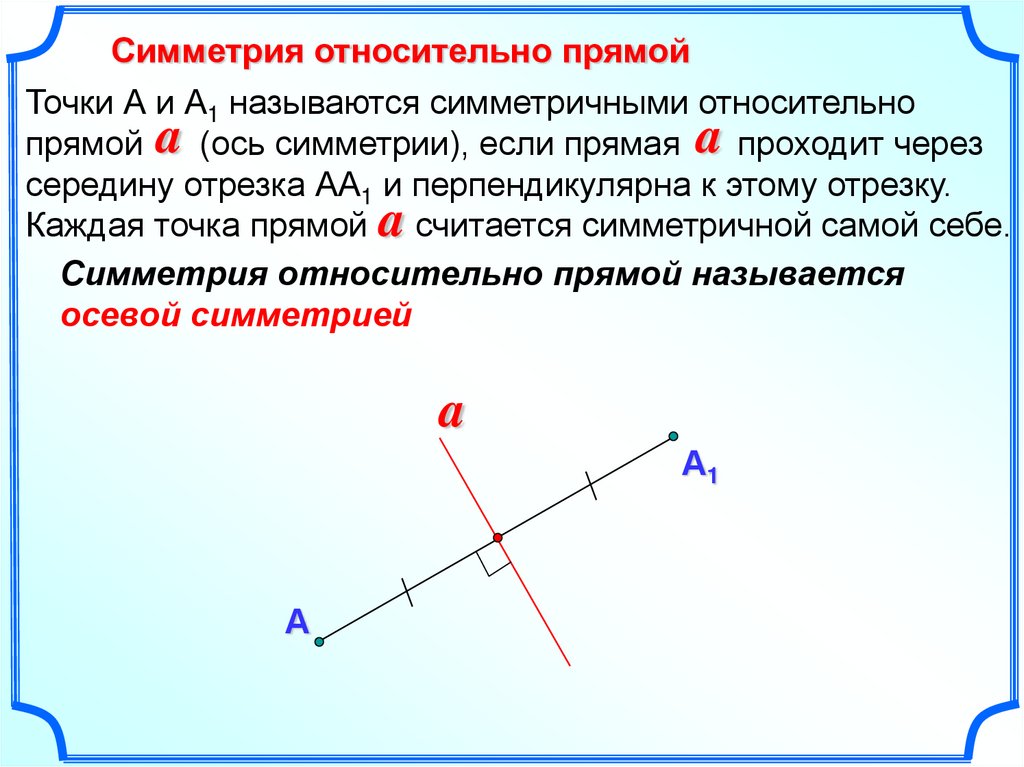
Симметрия относительно прямой
Точки А и А1 называются симметричными относительно
прямой a (ось симметрии), если прямая a проходит через
середину отрезка АА1 и перпендикулярна к этому отрезку.
Каждая точка прямой a считается симметричной самой себе.
Симметрия относительно прямой называется
осевой симметрией
a
А1
А

37.

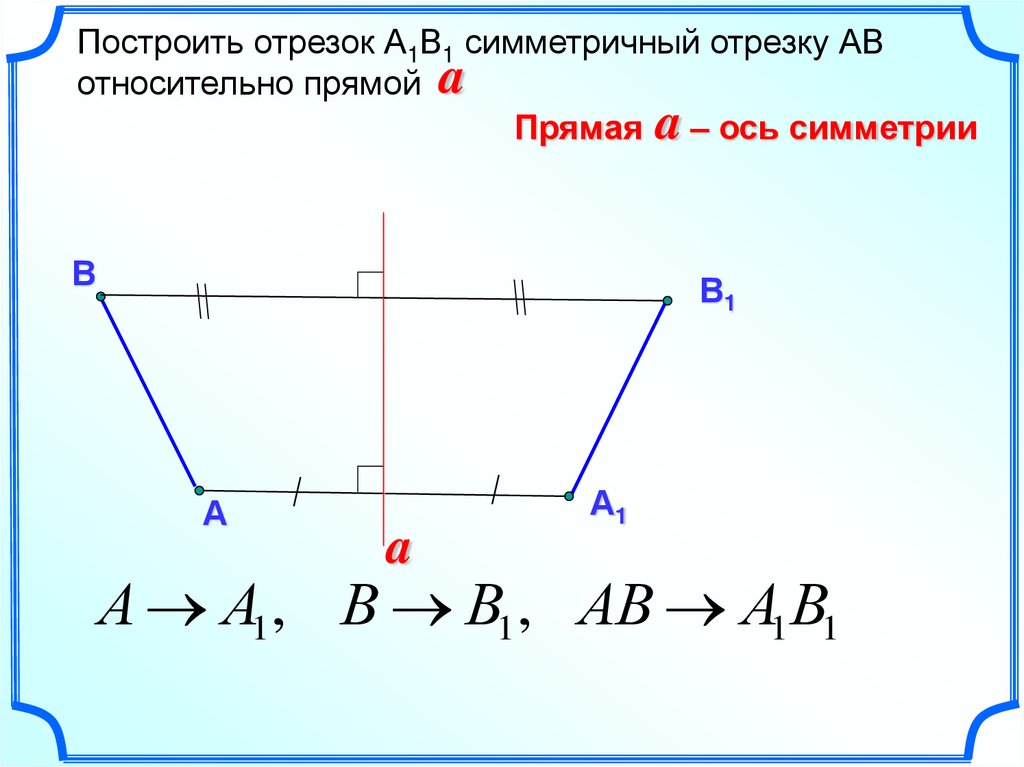
Построить отрезок А1В1 симметричный отрезку АВ
относительно прямой a
Прямая a – ось симметрии
В
В1
А
a
А1
А А1 , В В1 , АВ А1В1

38.

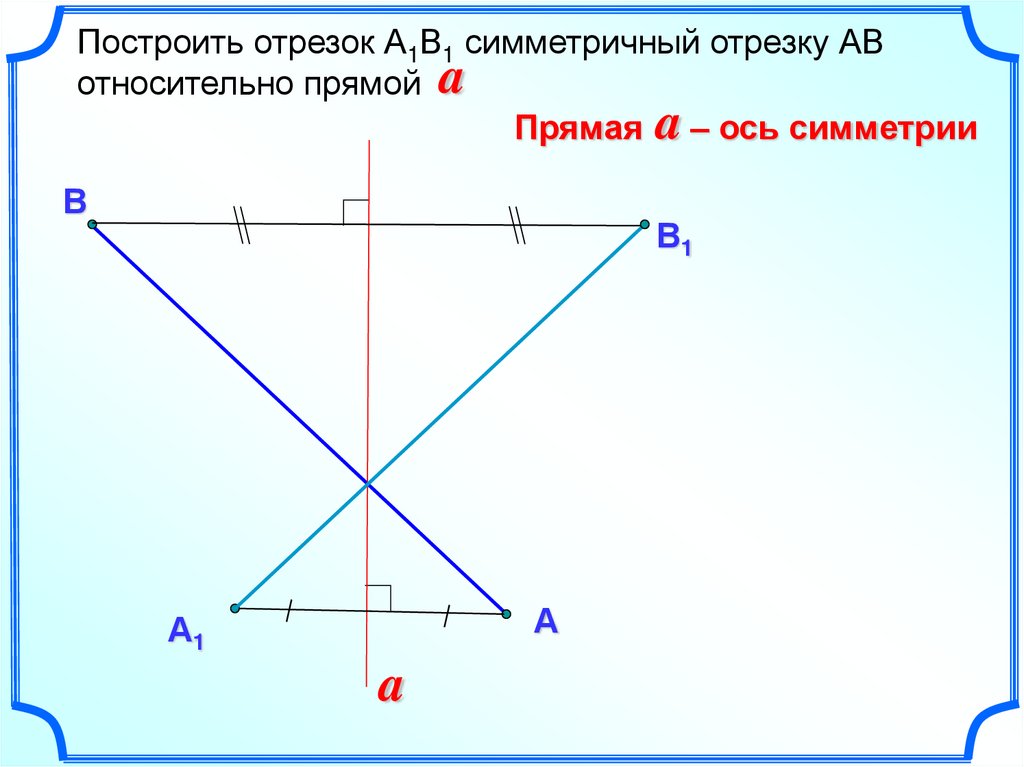
Построить отрезок А1В1 симметричный отрезку АВ
относительно прямой a
Прямая a – ось симметрии
В
В1
А
А1
a

39.

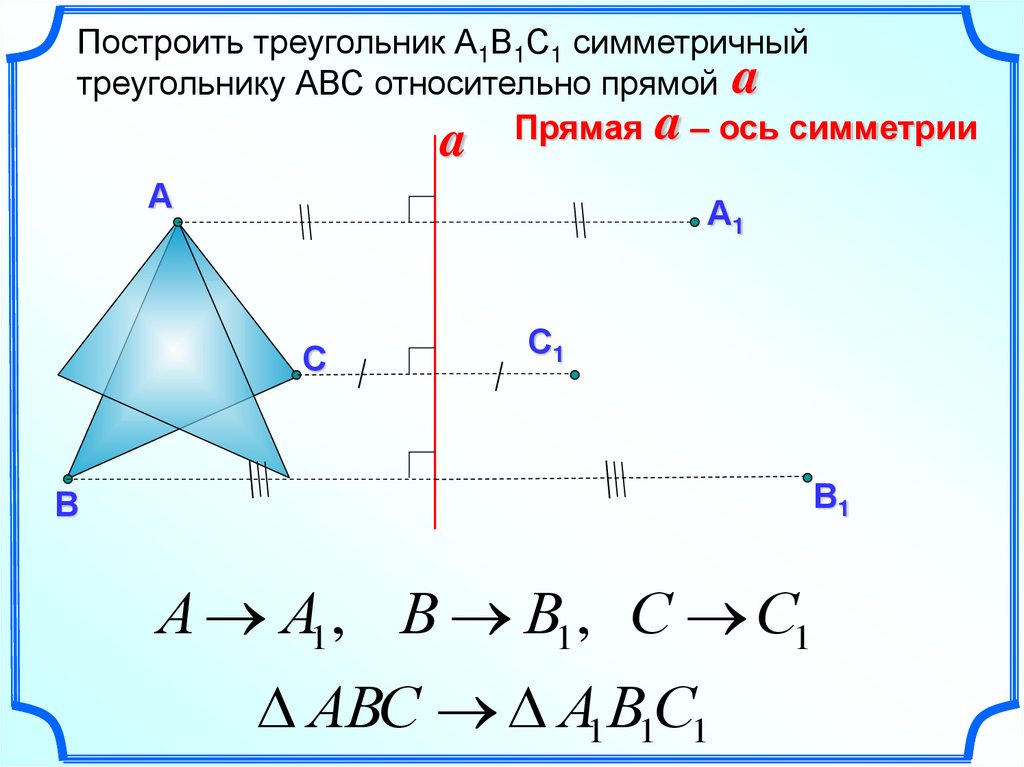
Построить треугольник А1В1С1 симметричный
треугольнику АВС относительно прямой a
a Прямая a – ось симметрии
А
А1
С
С1
В1
В
А А1 , В В1 , С С1
АВС А1В1С1

40.

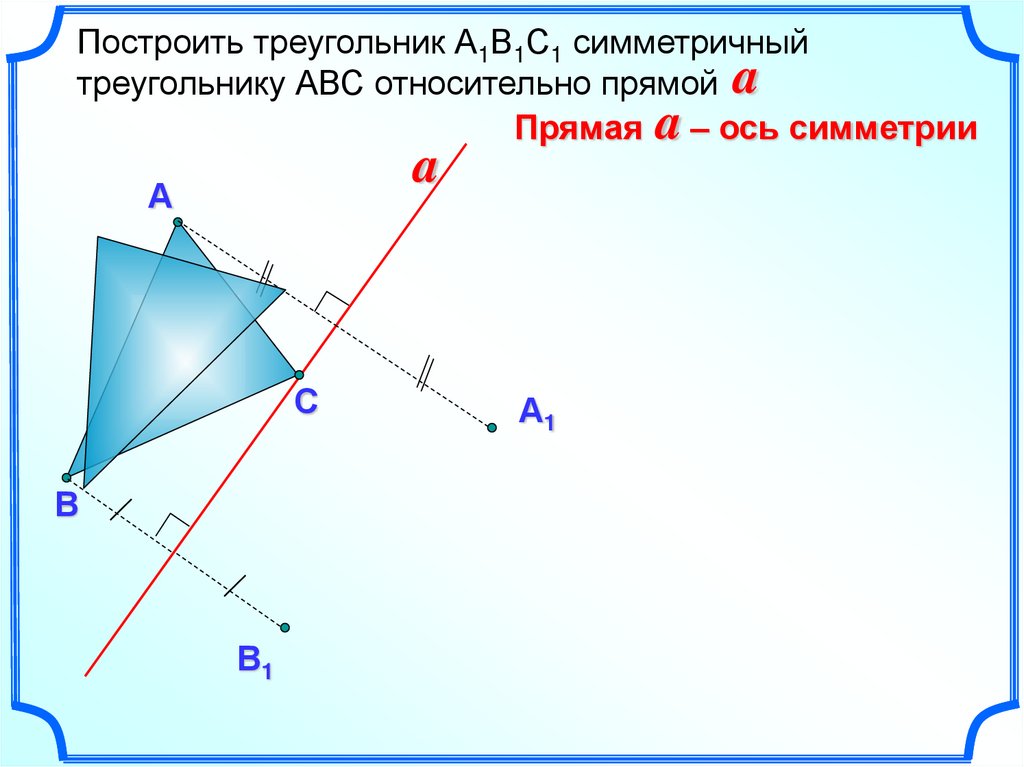
Построить треугольник А1В1С1 симметричный
треугольнику АВС относительно прямой a
Прямая a – ось симметрии
a
А
С
В
В1
А1

41.

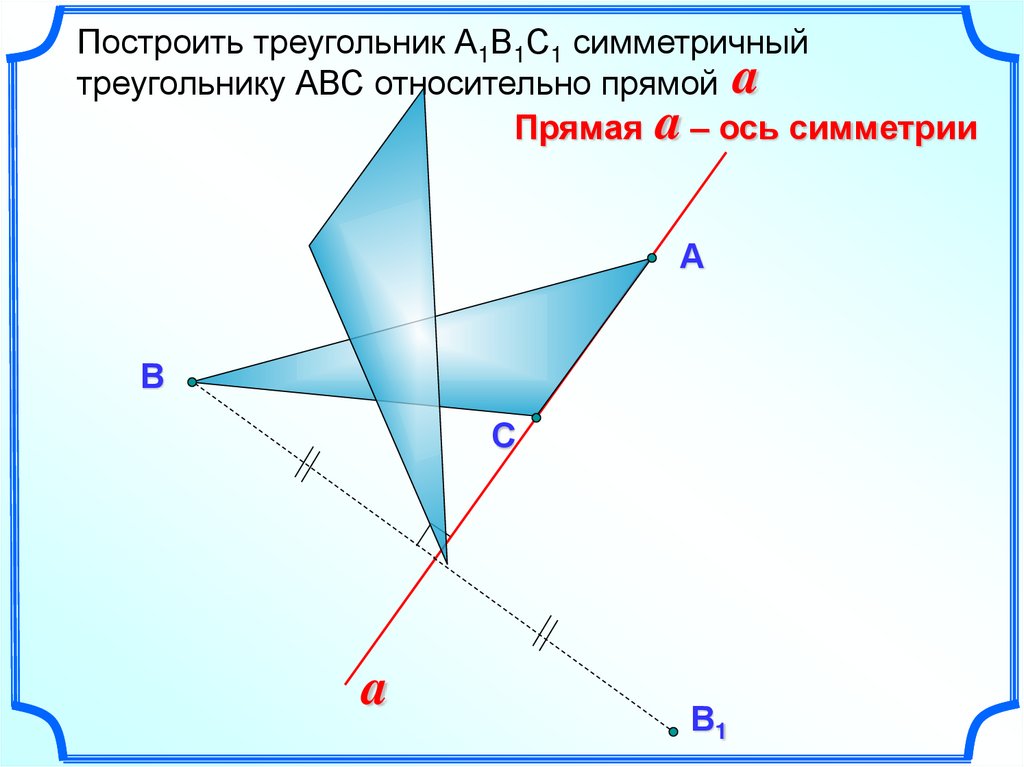
Построить треугольник А1В1С1 симметричный
треугольнику АВС относительно прямой a
Прямая a – ось симметрии
А
В
С
a
В1

42.

Прямая a – ось симметрии
А
А1
С1
В
С
a
В1

43.

Прямая m – ось симметрии
m

44.

Прямая а – ось симметрии
A
A1
a
B
B1
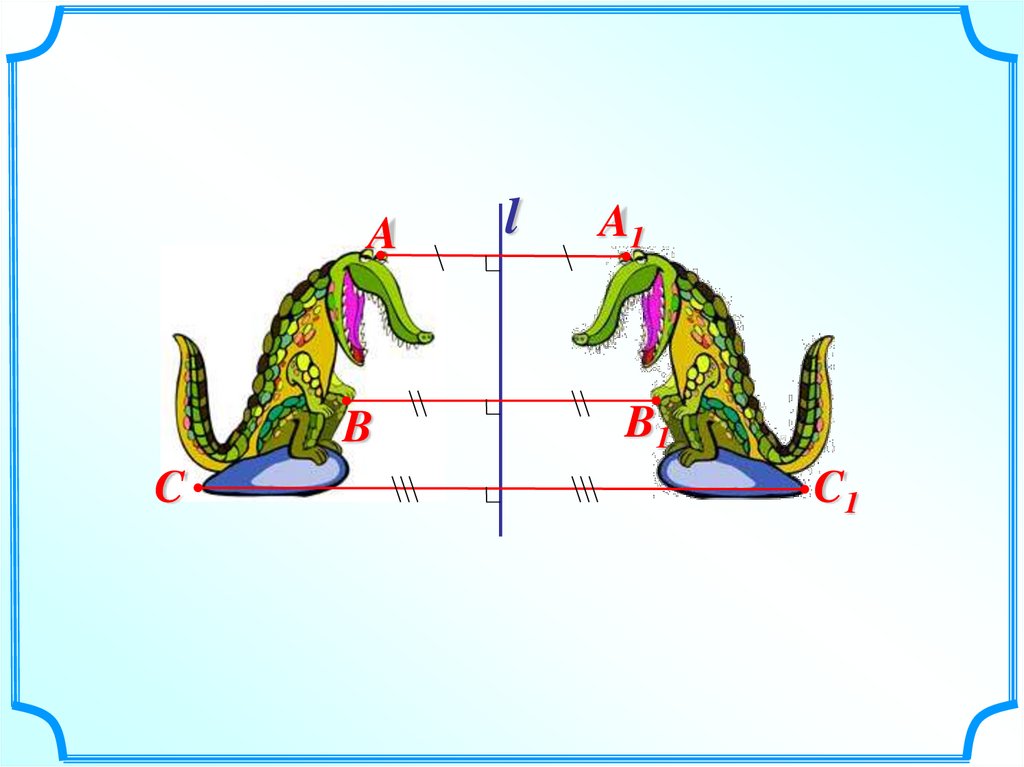
C
C1

45.

A
B
C
l
A1
B1
C1

46.

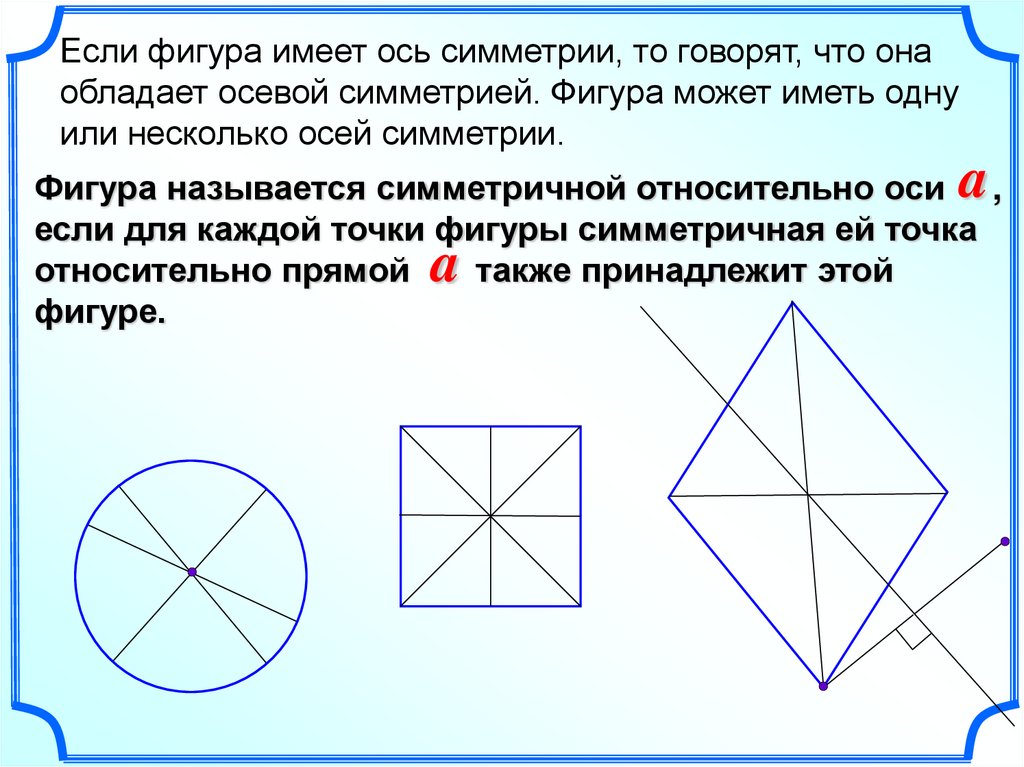
Если фигура имеет ось симметрии, то говорят, что она
обладает осевой симметрией. Фигура может иметь одну
или несколько осей симметрии.
a
Фигура называется симметричной относительно оси ,
если для каждой точки фигуры симметричная ей точка
относительно прямой
также принадлежит этой
фигуре.
a

47.

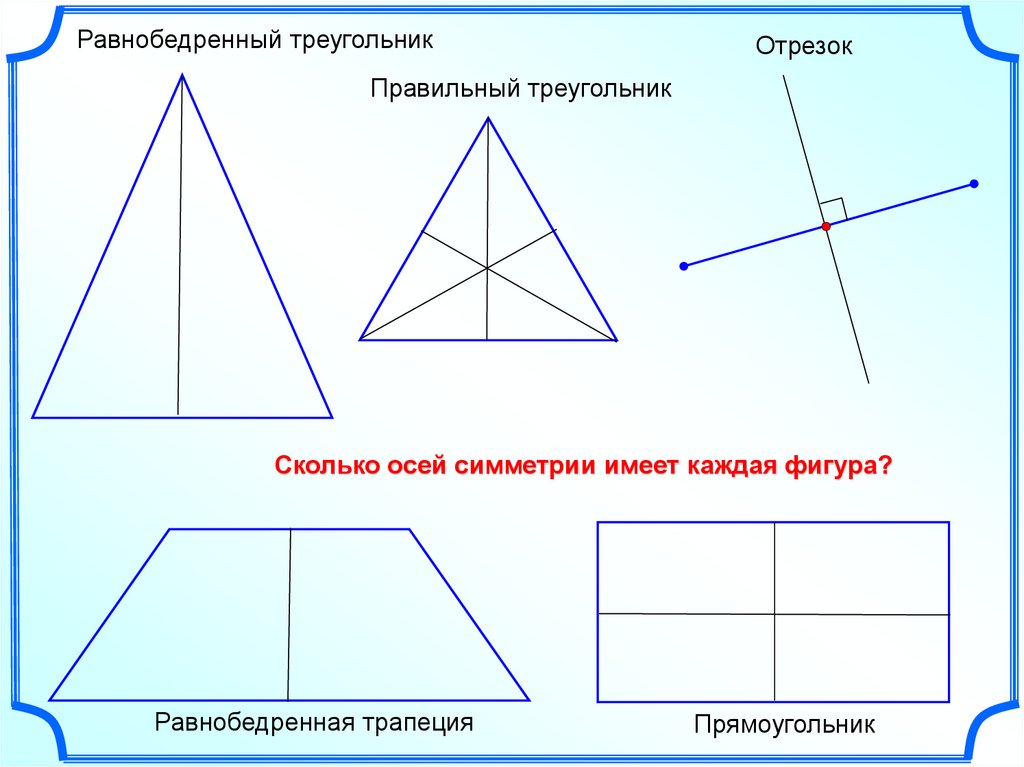
Равнобедренный треугольник
Отрезок
Правильный треугольник
Сколько осей симметрии имеет каждая фигура?
Равнобедренная трапеция
Прямоугольник

48.

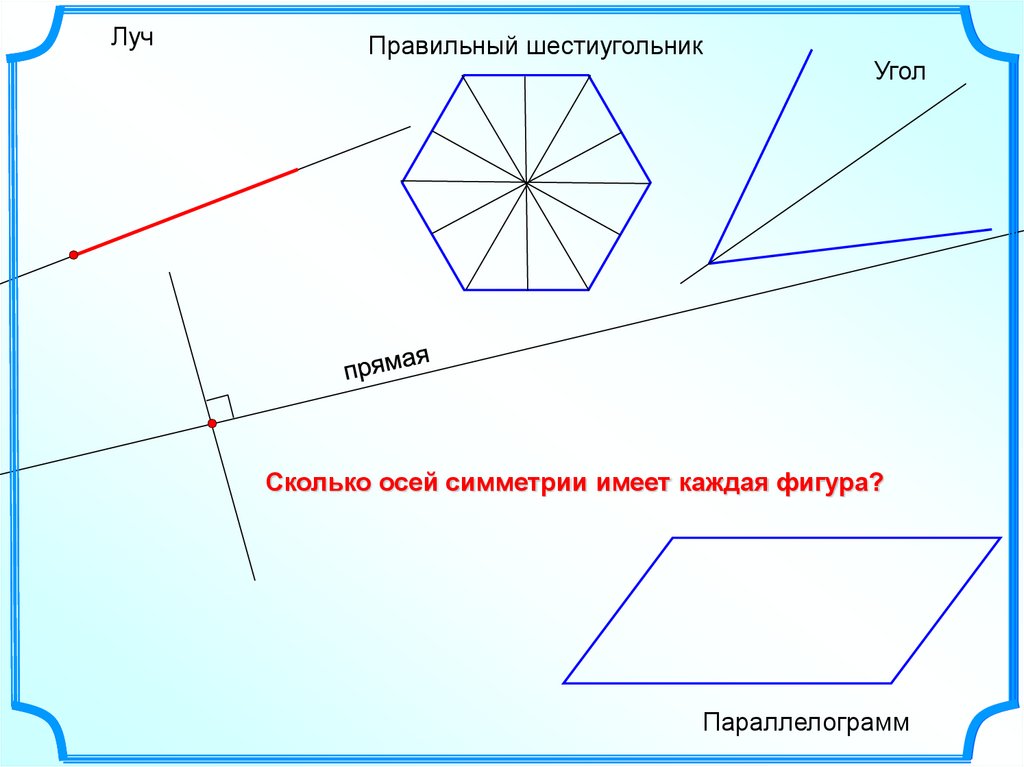
Луч
Правильный шестиугольник
Угол
Сколько осей симметрии имеет каждая фигура?
Параллелограмм

49.

Какие буквы имеют ось симметрии?
А БФ Г 0 Э
Ю ЖН П Ш

50.

Какие буквы имеют ось симметрии?
RYSV Х С
DWU М В

51.

Симметрия в природе
http://2krota.ru/2009/06/27/babochki-chast-2.html
http://2krota.ru/uploads/posts/2009-06/1245402488_822717426.jpg

52.

Симметрия в танцевальной постановке необходима, однако для
произведения должного эффекта она должна сопровождаться
асимметрией
http://www.idance.ru/articles/20/767p_sy4.jpg

53.

Символ вечной любви, Индии, симметрии, торжества персидской
архитектуры - мавзолей Тадж-Махал
http://www.indostan.ru/indiya/foto-video/2774/3844_9_o.jpg

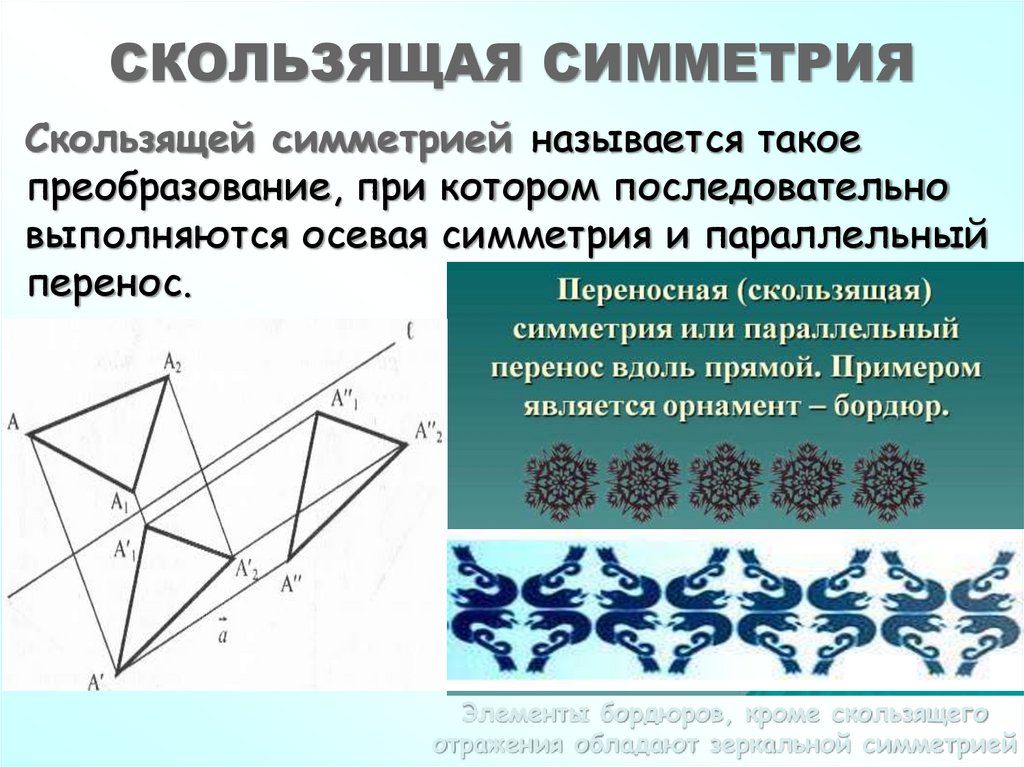
54. СКОЛЬЗЯЩАЯ СИММЕТРИЯ

Скользящей симметрией называется такое
преобразование, при котором последовательно
выполняются осевая симметрия и параллельный
перенос.
Элементы бордюров, кроме скользящего
отражения обладают зеркальной симметрией

55. ЗЕРКАЛЬНАЯ СИММЕТРИЯ

Если преобразование симметрии относительно
плоскости переводит фигуру (тело) в себя, то
фигура называется симметричной относительно
плоскости, а данная плоскость – плоскостью
симметрии этой фигуры.

56.

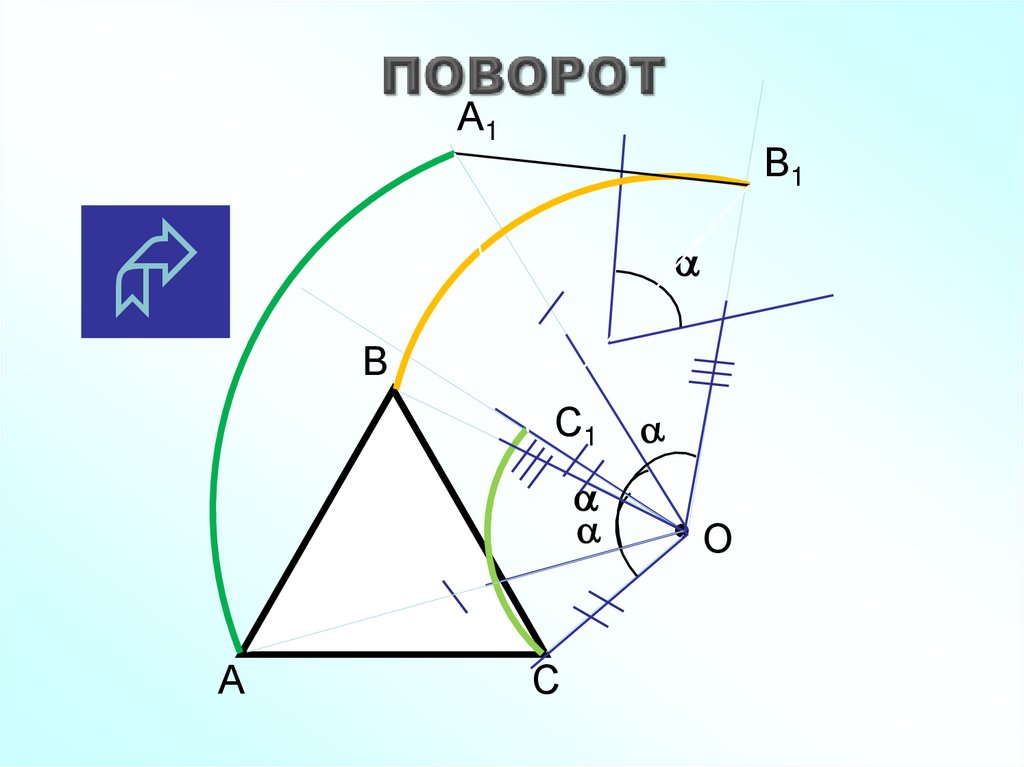
57.

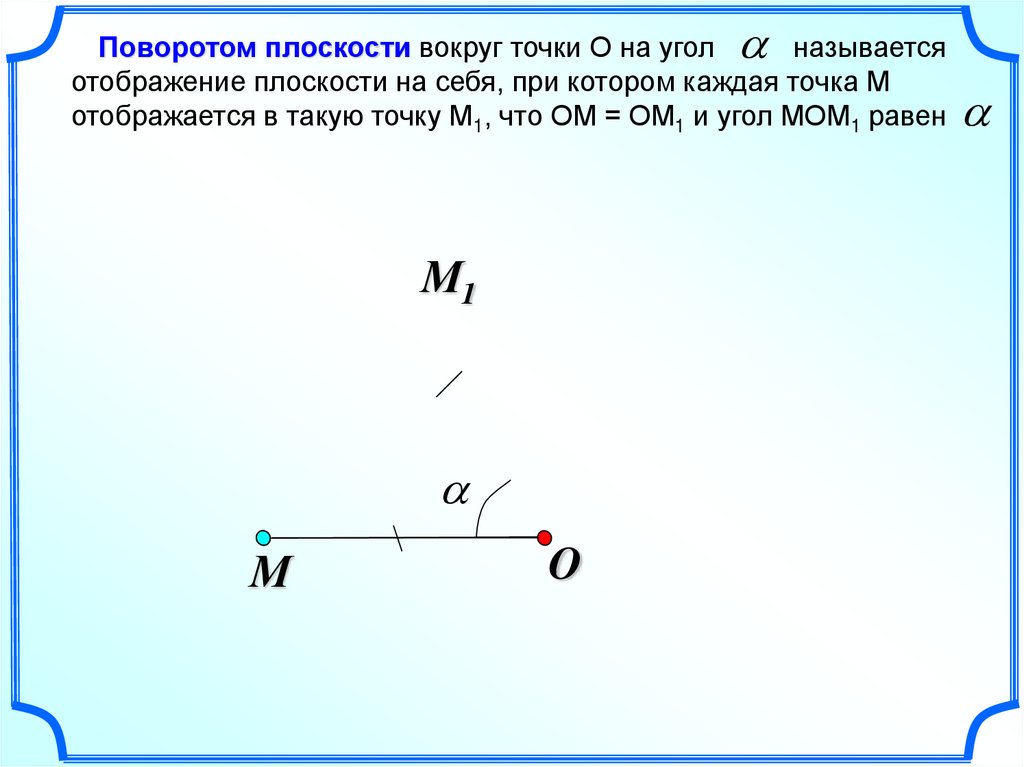
Поворотом плоскости вокруг точки О на угол
называется
отображение плоскости на себя, при котором каждая точка М
отображается в такую точку М1, что ОМ = ОМ1 и угол МОМ1 равен
М1
М
O

58.

Угол поворота 600
110
100
130
60
70
100
80
40
30
140
30
150
160
20
170
180
50
110
130
40
160
М160
120
50
150
70
90
120
140
80
20
10
170
10
0
180
0
О
М

59.

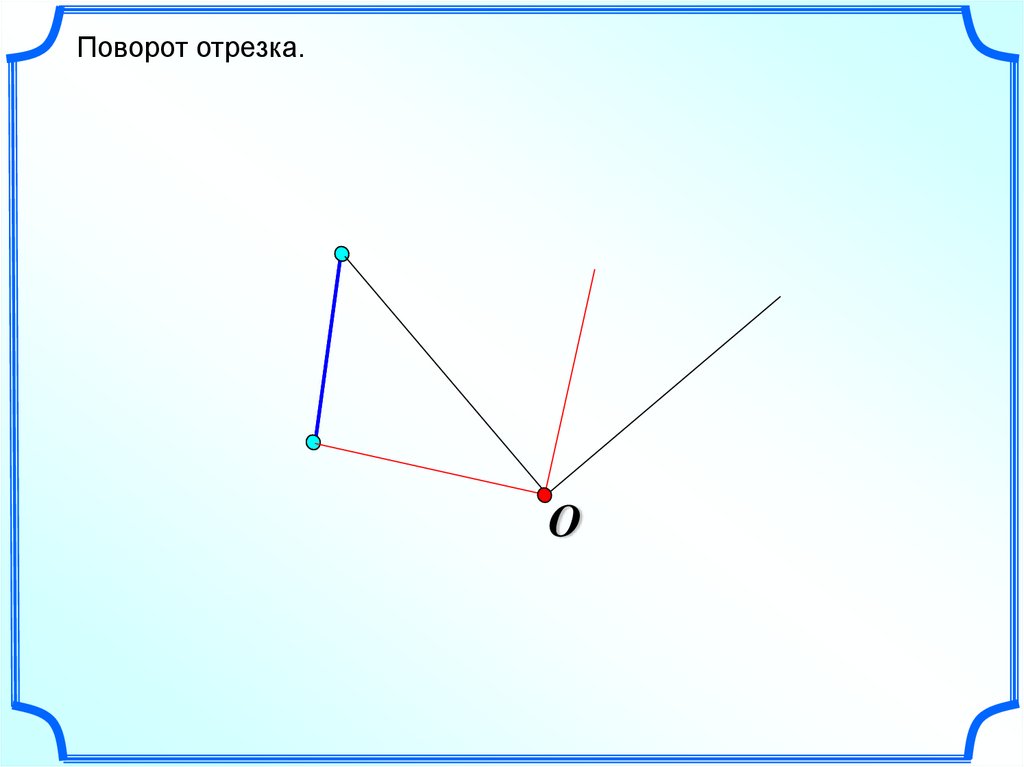
Поворот отрезка.
O

60.

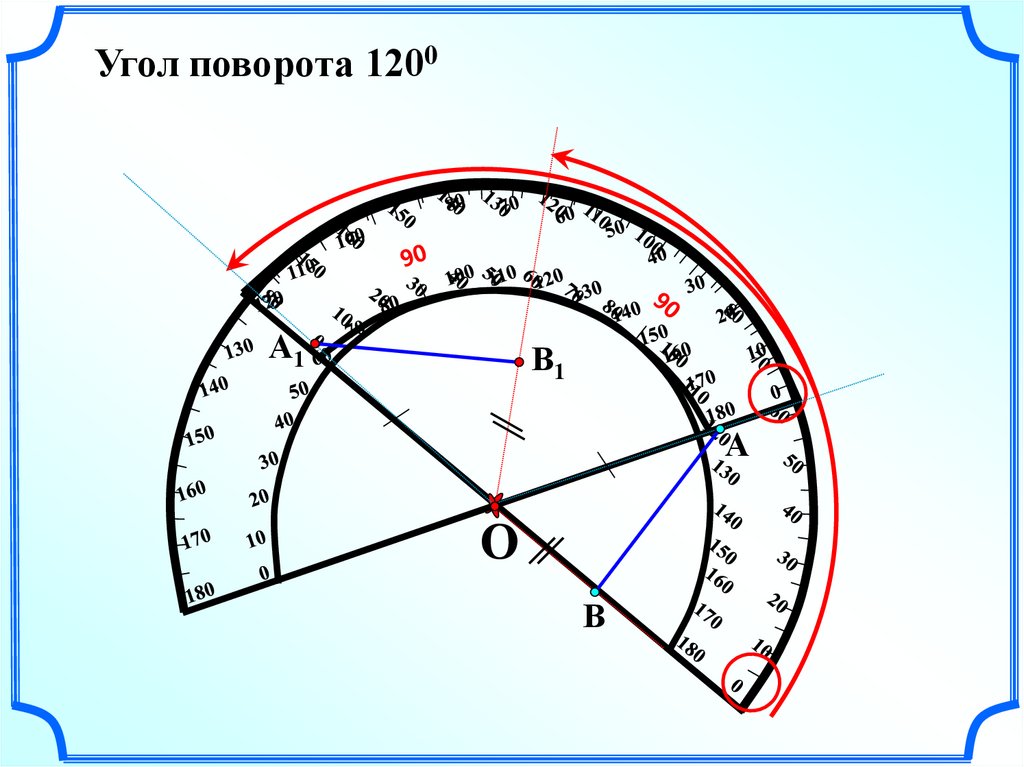
Угол поворота 1200
А1
В1
А
О
В

61.

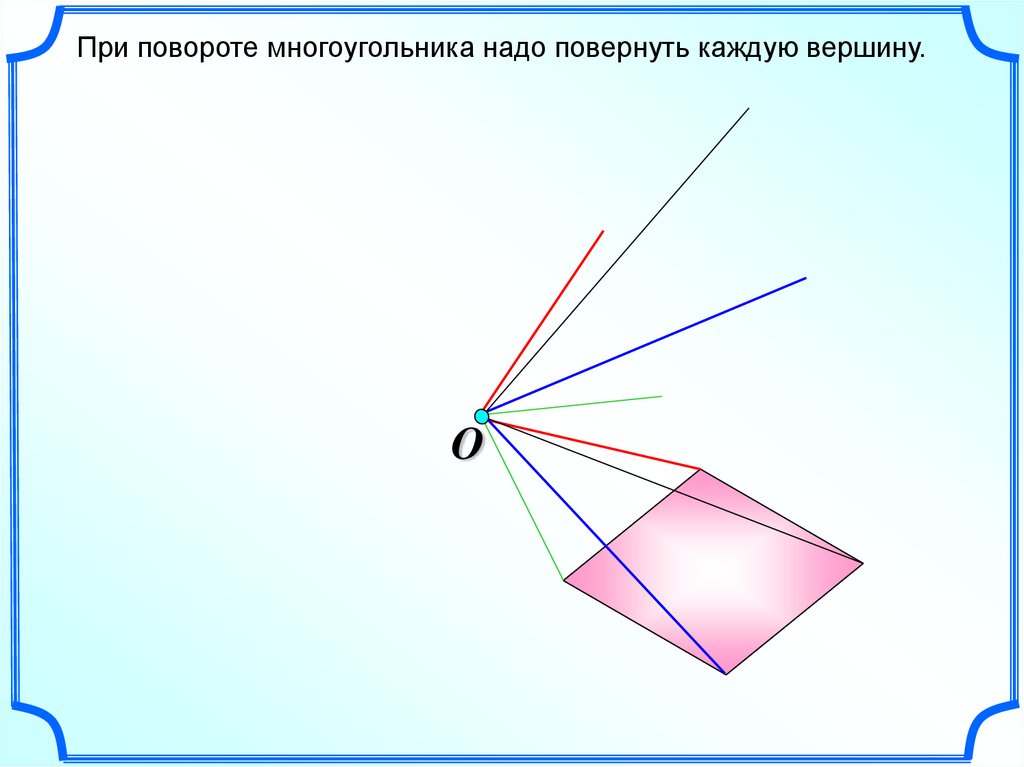
При повороте многоугольника надо повернуть каждую вершину.
O

62.

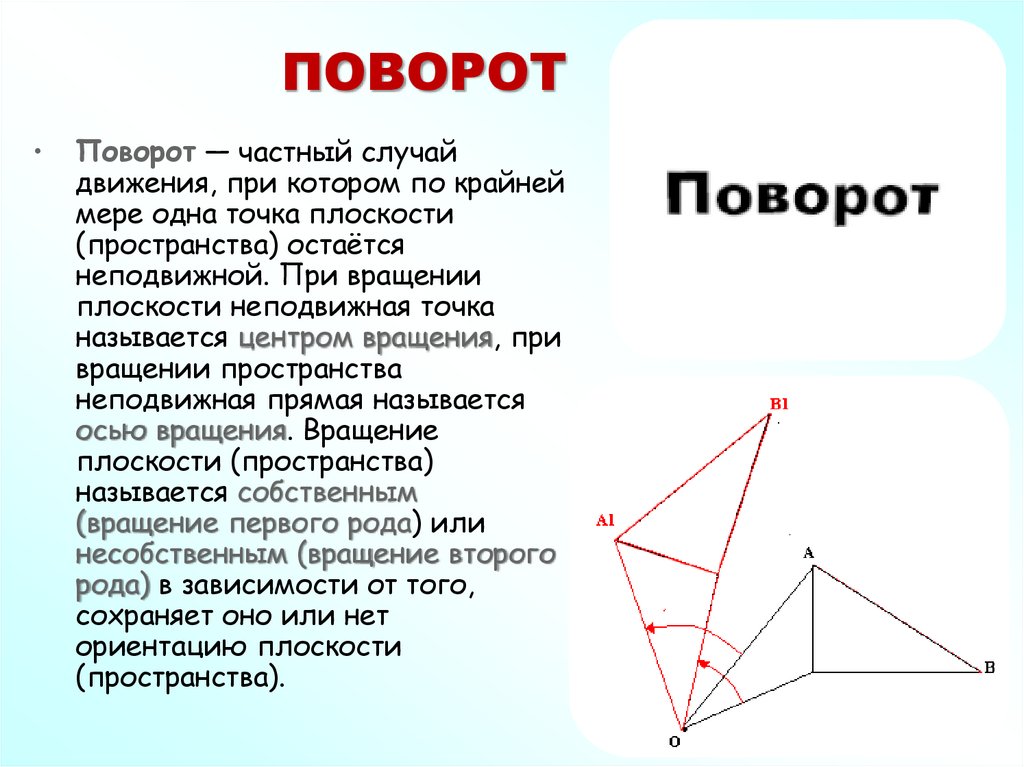
63. ПОВОРОТ

Поворот — частный случай
движения, при котором по крайней
мере одна точка плоскости
(пространства) остаётся
неподвижной. При вращении
плоскости неподвижная точка
называется центром вращения, при
вращении пространства
неподвижная прямая называется
осью вращения. Вращение
плоскости (пространства)
называется собственным
(вращение первого рода) или
несобственным (вращение второго
рода) в зависимости от того,
сохраняет оно или нет
ориентацию плоскости
(пространства).

64. ПОВОРОТ

А1
В1
В
С1
А
С
О

65. Вывод:

ПОВОРОТ
Чтобы получить отображение фигуры при
повороте около данной точки, нужно каждую
точку фигуры повернуть на один и тот же угол
в одном и том же направлении:
по часовой стрелке;
против часовой стрелки.

66.

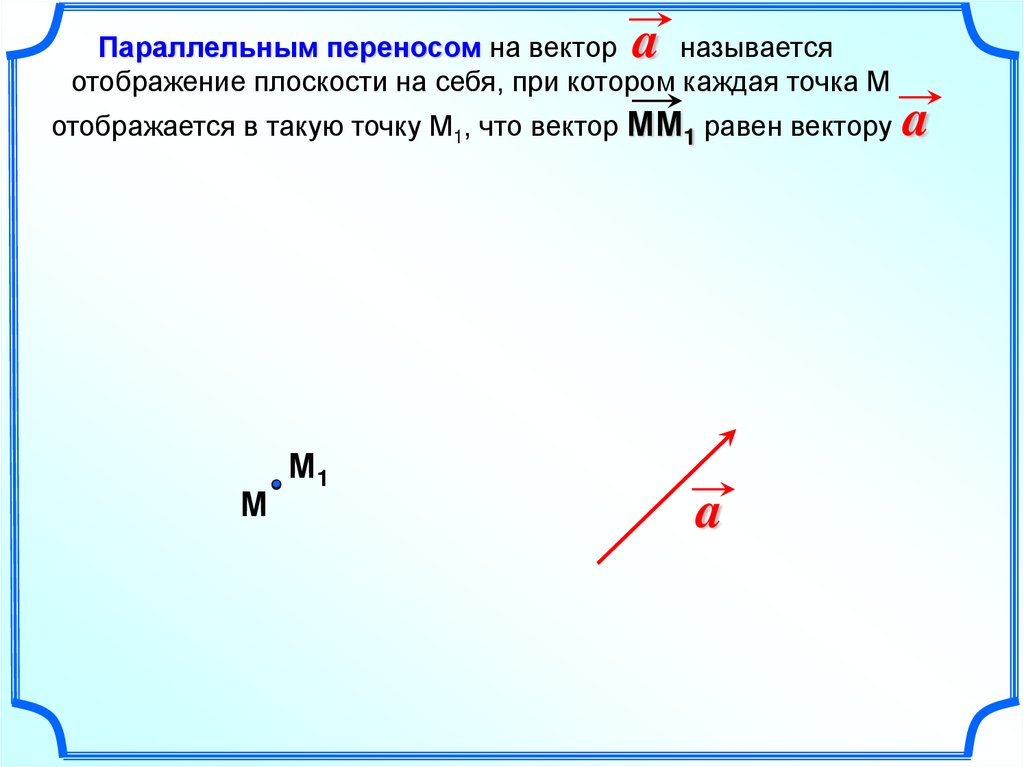
a
Параллельным переносом на вектор
называется
отображение плоскости на себя, при котором каждая точка М
отображается в такую точку М1, что вектор ММ1 равен вектору
М
М1
a
a

67.

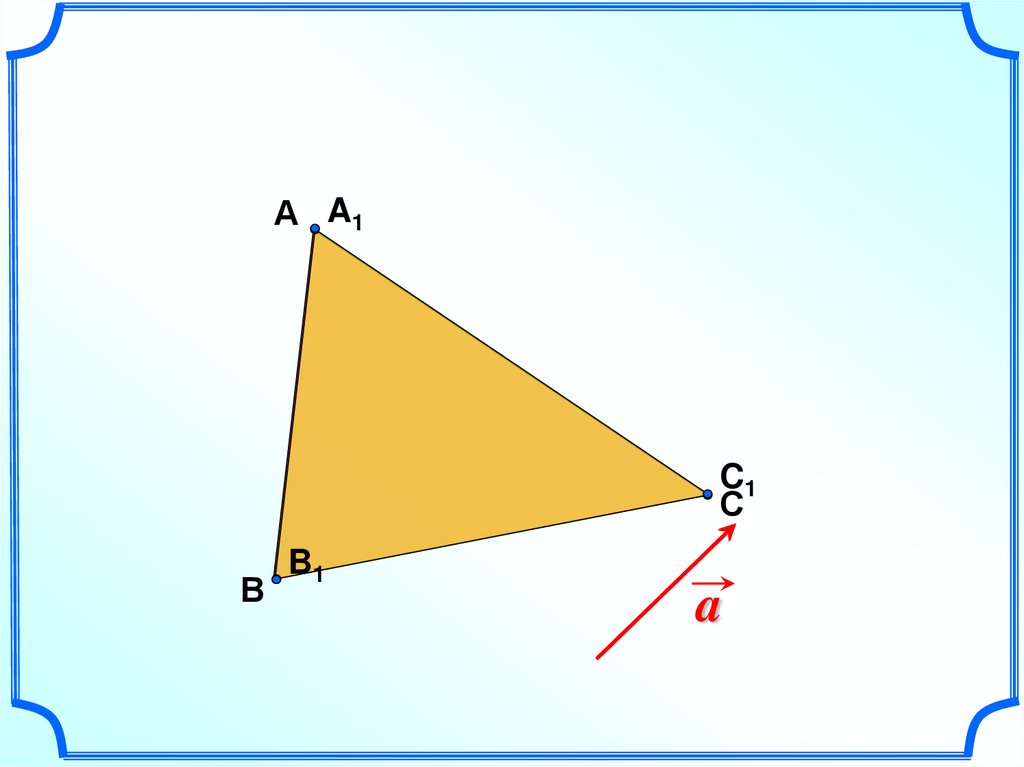
А A1
C1
С
В
B1
a

68.

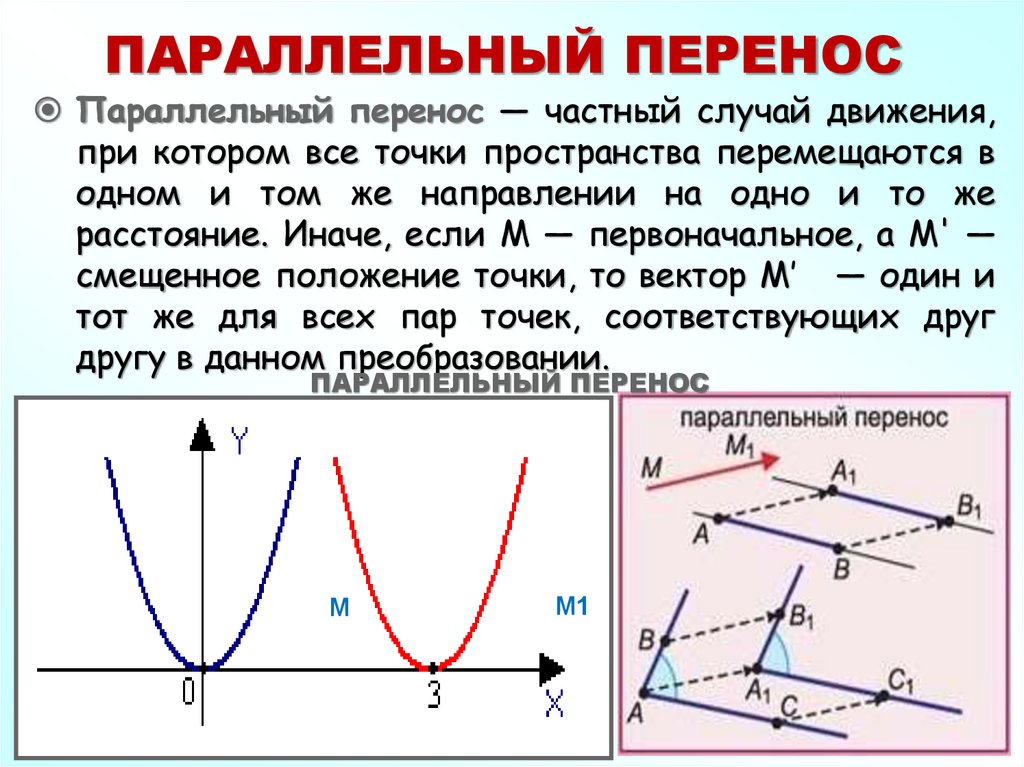
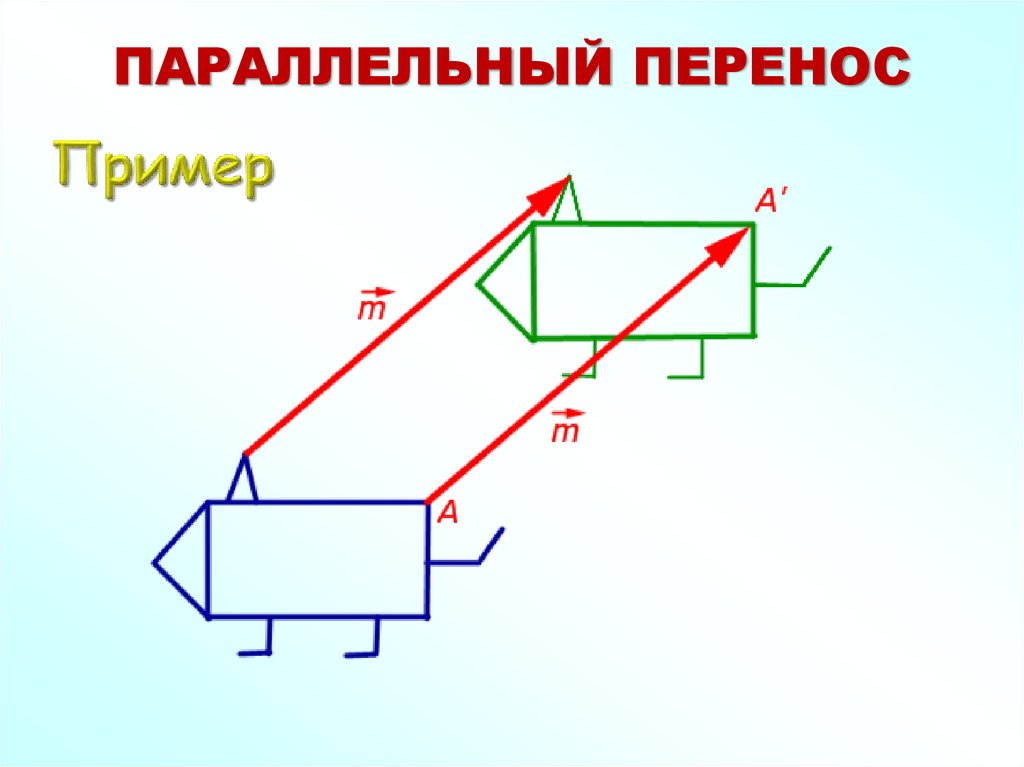
a

69. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС

Параллельный перенос ― частный случай движения,
при котором все точки пространства перемещаются в
одном и том же направлении на одно и то же
расстояние. Иначе, если M ― первоначальное, а M' ―
смещенное положение точки, то вектор M’ ― один и
тот же для всех пар точек, соответствующих друг
другу в данном преобразовании.
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
М
М1

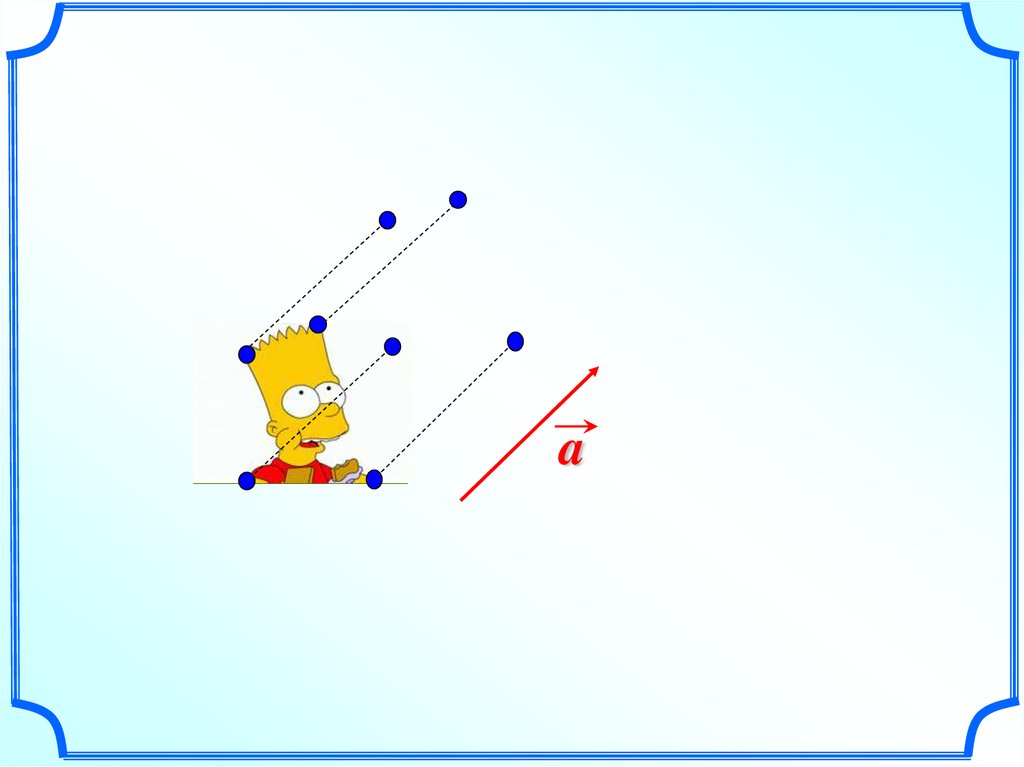
70. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС

71. РОЛЬ СИММЕТРИИ В МИРЕ

Как бы нам жилось без симметрии?
Какую роль играет симметрия в нашем мире? Неужели она
лишь украшает его?
Оказывается, что без симметрии наш мир выглядел бы
совсем по-другому. Ведь это именно на симметрии
основаны многие законы сохранения. Например, законы
сохранения энергии, импульса и момента импульса
являются
следствиями
пространственно-временных
симметрий, которые являются, как математическими, так
и физическими симметриями. И без этих симметрий не
было бы законов сохранений, которые во многом
управляют нашим миром.
Так что симметрия – пожалуй, чуть ли не самая главная
вещь во Вселенной.

72. СИММЕТРИЯ В ОКРУЖАЮЩЕМ НАС МИРЕ

73. Заключение

ДВИЖЕНИЕ И ВСЕ ЕГО ВИДЫ
ЯВЛЯЮТСЯ НЕОТЪЕМЛЕМОЙ И
ВАЖНОЙ КОМПОНЕНТОЙ
СУЩЕСТВОВАНИЯ ЧЕЛОВЕЧЕСТВА.
БЕЗ ДВИЖЕНИЙ НЕ БЫЛО БЫ ВСЕГО
ТОГО, ЧТО НАС ОКРУЖАЕТ,
ВДОХНОВЛЯЕТ, РАДУЕТ И МОТИВИРУЕТ
ЖИТЬ И ТВОРИТЬ.

74.

75.

76.

Задание на дом:
1) используя учебник и презентацию конспект по теме
«Симметрия относительно точки» п.113-115, № 1150,
№ 1155
2) используя учебник и презентацию конспект по теме
«Симметрия относительно прямой» п.113-115, № 1156,
№ 1161
3) используя учебник и презентацию конспект по теме
«Поворот и параллельный перенос» п.116-117, № 1163,
№ 1166