Движения. Виды движения. Свойства движения. Задачи на построение

1. Геометрия 9класс

Тема «Движения»

2. Содержание

Определение
Виды движения
Свойства движения
Задачи на построение
Примеры движения в курсе алгебры
Движение вокруг нас

3.

Любое отображение, при
котором сохраняется расстояние
между точками , называется
ДВИЖЕНИЕМ.

4.

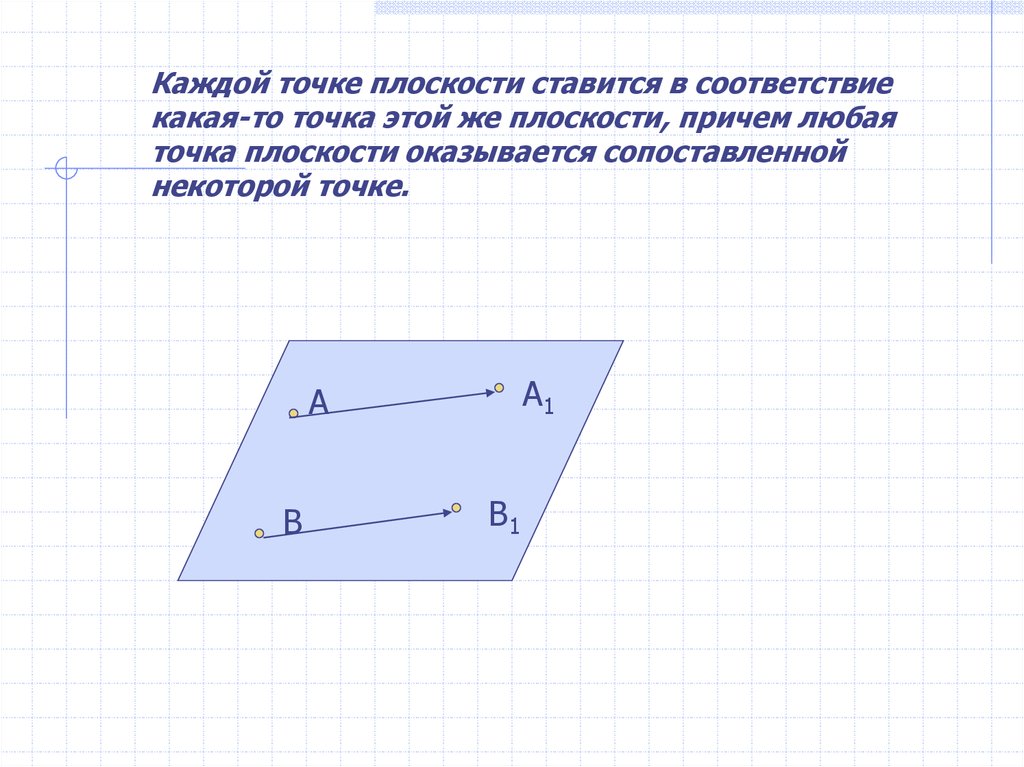
Каждой точке плоскости ставится в соответствие
какая-то точка этой же плоскости, причем любая
точка плоскости оказывается сопоставленной
некоторой точке.
А1
А
В
В1

5.

При движении отрезок отображается на
отрезок.
С
D
C1
D1
CD=C1D1

6.

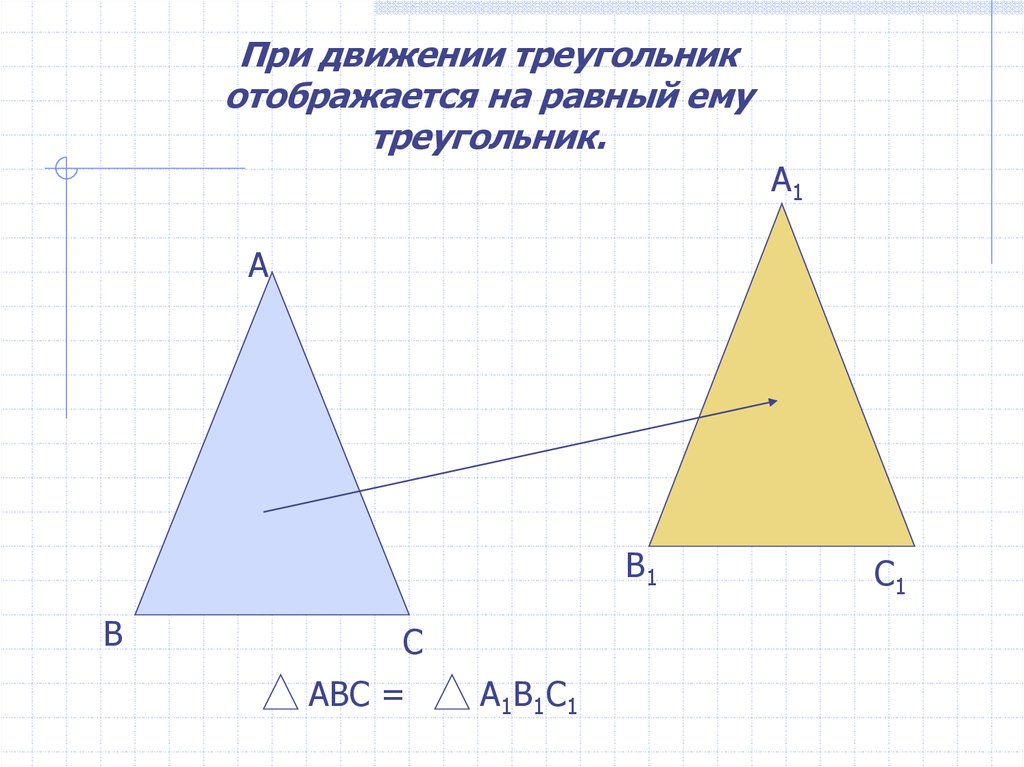
При движении треугольник
отображается на равный ему
треугольник.
А1
А
В1
В
С
АВС =
А1В1С1
С1

7.

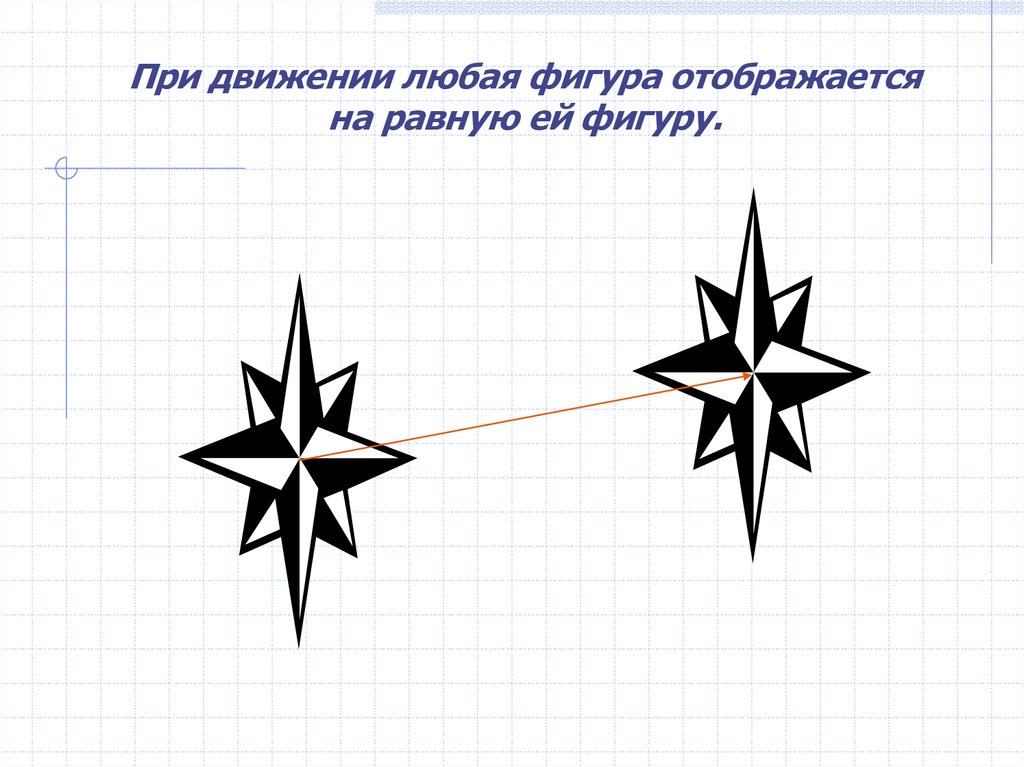
При движении любая фигура отображается
на равную ей фигуру.

8.

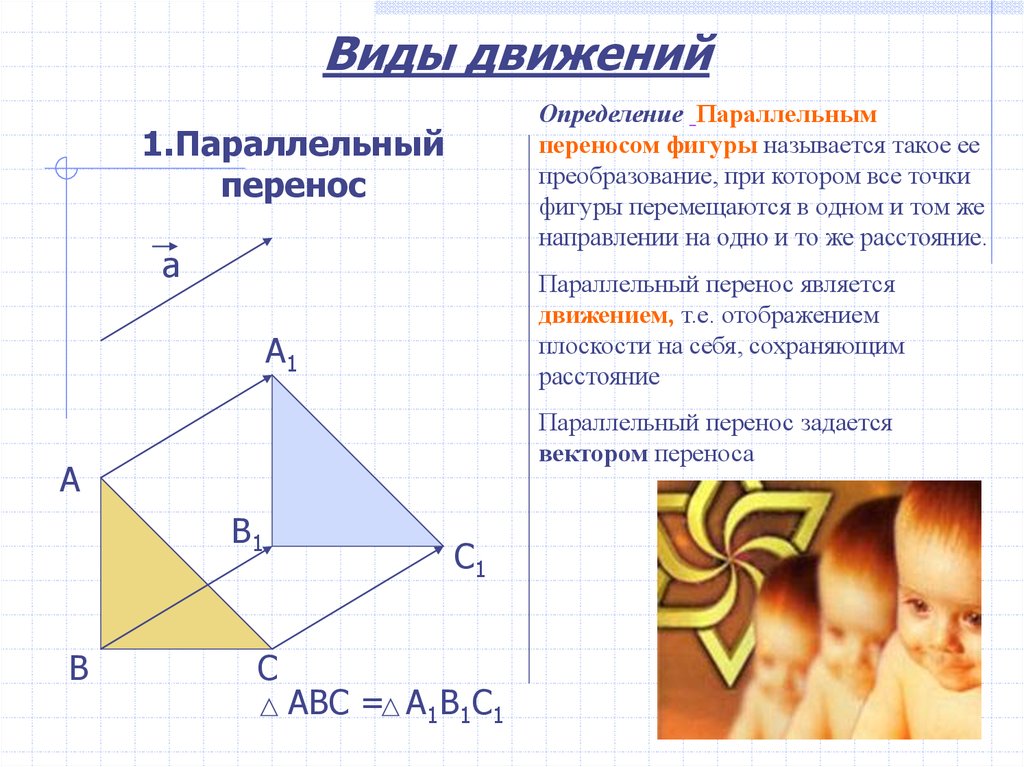
Виды движений
Определение Параллельным
переносом фигуры называется такое ее
преобразование, при котором все точки
фигуры перемещаются в одном и том же
направлении на одно и то же расстояние.
1.Параллельный
перенос
а
Параллельный перенос является
движением, т.е. отображением
плоскости на себя, сохраняющим
расстояние
A1
Параллельный перенос задается
вектором переноса
A
B1
B
C
C1
АВС = А1В1С1

9.

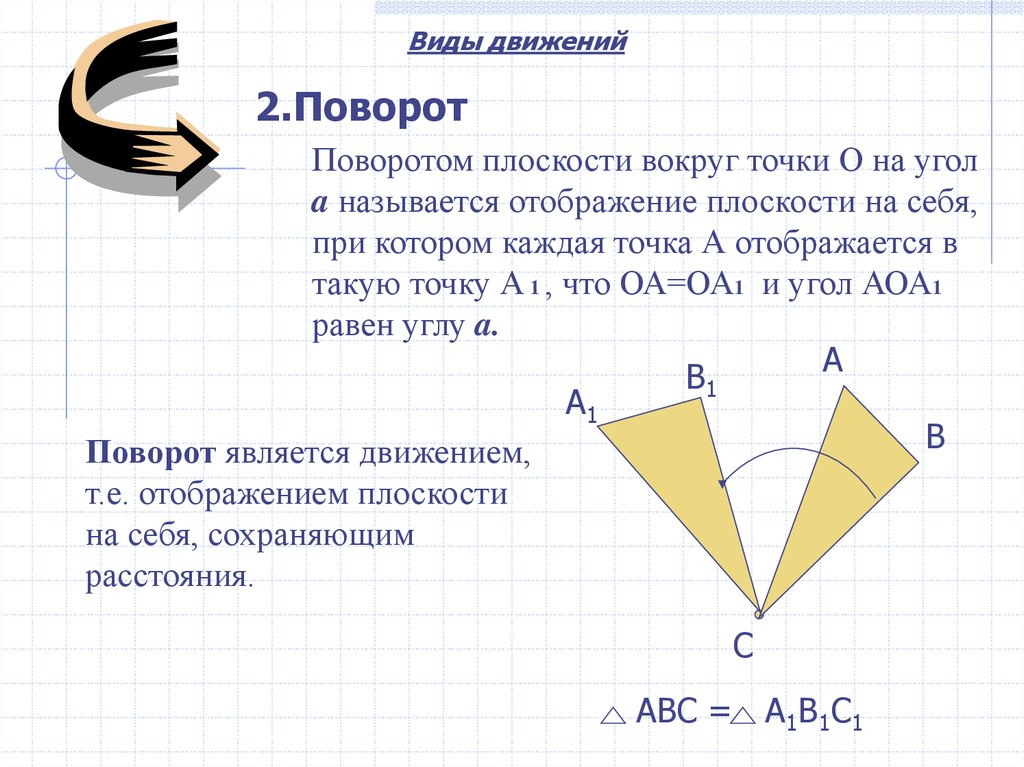
Виды движений
2.Поворот
Поворотом плоскости вокруг точки О на угол
a называется отображение плоскости на себя,
при котором каждая точка А отображается в
такую точку А 1 , что ОА=ОА1 и угол АОА1
равен углу a.
A
B1
A1
B
Поворот является движением,
т.е. отображением плоскости
на себя, сохраняющим
расстояния.
C
АВС = А1В1С1

10.

Особый случай
представляет поворот на 180
градусов. Пусть т.О – центр
поворота. Чтобы построить точку
соответствующую точке X,
достаточно продолжить отрезок
XО за точку О на отрезок
Х
О
ОХ1 = ОX.
Точки Х 1 и X называются
симметричными относительно
точки О.
Точка О - есть центр симметрии.
Х
1

11.

3.Центральная
симметрия
Основное свойство
центральной симметрии:
М
Центральная, симметрия
является движением
изменяющим направления
на противоположные
M1N1K1= MNK
K
N
O
K1
N1
М1

12.

4.Осевая симметрия
Фигура F , полученная
отражением фигуры F
относительно прямой n,
называется симметричной
фигуре F относительно прямой n.
P1Q1S1= PQS
P
P1
Точки P и P1
называются
симметричными
относительно прямой n .
Прямая n серединный
перпендикуляр отрезка PP1. .
Осевая симметрия обладает
следующим свойством – это
отображение плоскости на себя,
которое сохраняет расстояние
между точками.
Q
Q1
S
n
S1

13. Знаете ли вы, что…

Слово симметрия означает «соразмерность».
Под симметрией в широком смысле этого слова
понимают всякую правильность во внутреннем
строении тела или фигуры.
Учение о различных видах симметрии представляет
большую и важную ветвь геометрии, тесно связанную
со многими отраслями естествознания и техники,
начиная с текстильного производства (разрисовка
тканей) и архитектурной мозаики, а кончая тонкими
вопросами строения вещества.

14.

15. Симметрия нас окружает всюду и в природе, и в архитектуре зданий, и в технике, и…

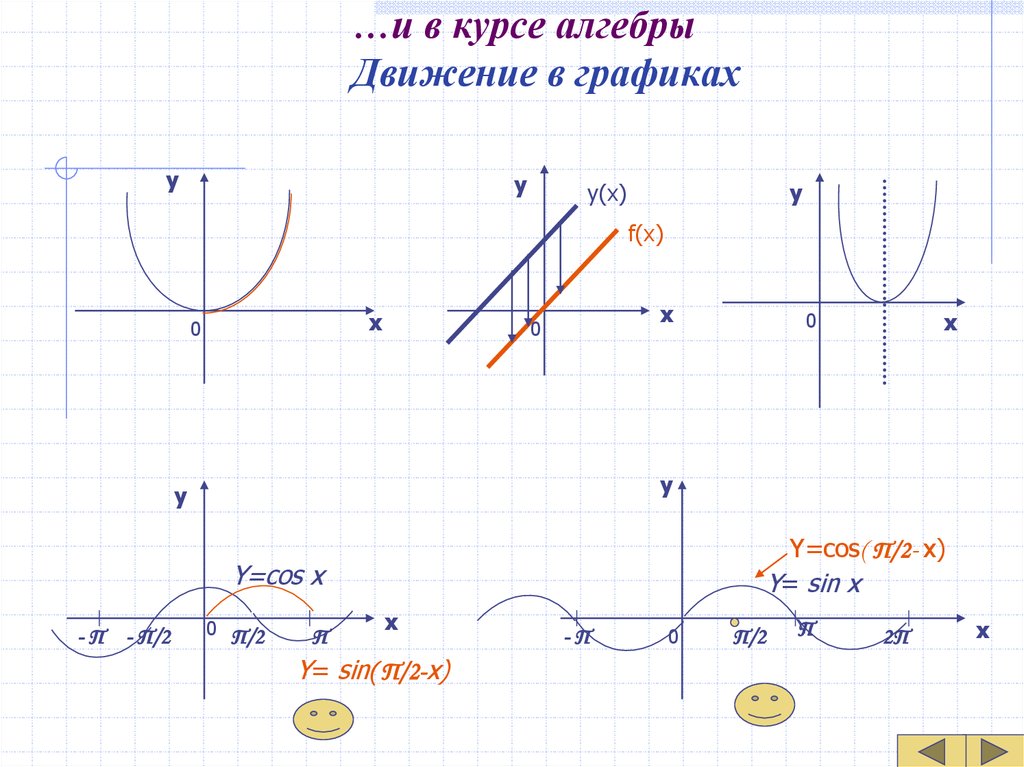
16. …и в курсе алгебры Движение в графиках

у
у
y(x)
у
f(x)
х
0
х
0
х
у
у
Y=cos( П/2- x)
Y= sin x
Y=cos x
- П - П/2
0
0 П/2
П
х
Y= sin( П/2-x)
-П
0
П/2
П
2П
х

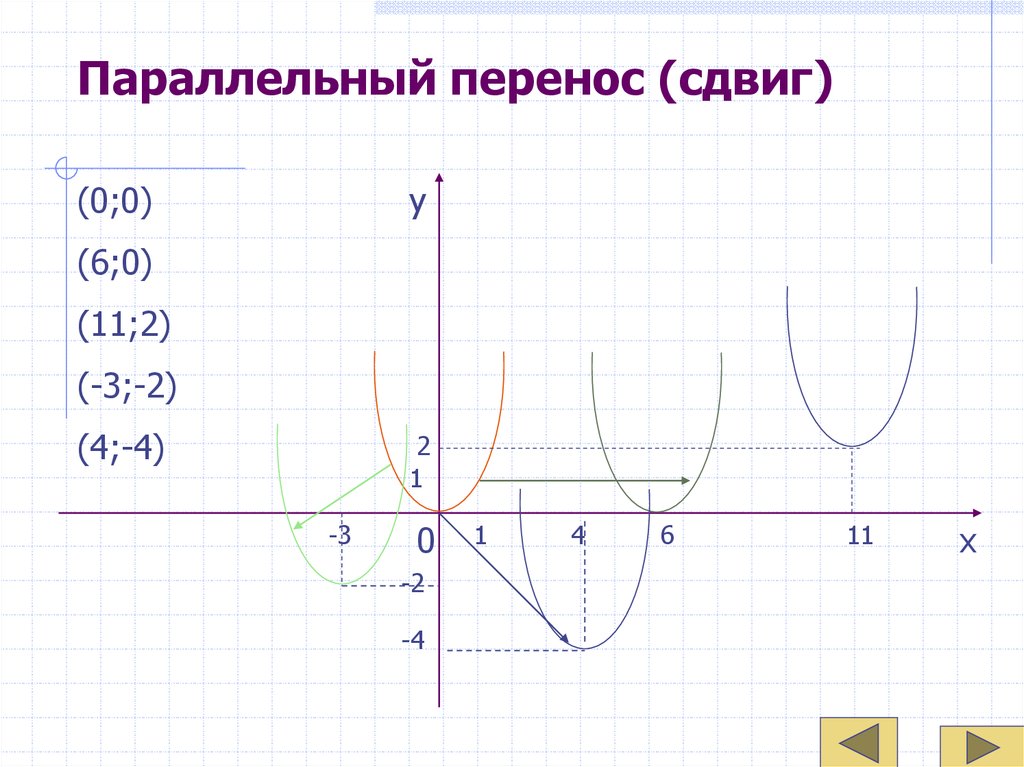
17. Параллельный перенос (сдвиг)

(0;0)
y
(6;0)
(11;2)
(-3;-2)
(4;-4)
2
1
-3
0
-2
-4
1
4
6
11
x

18.

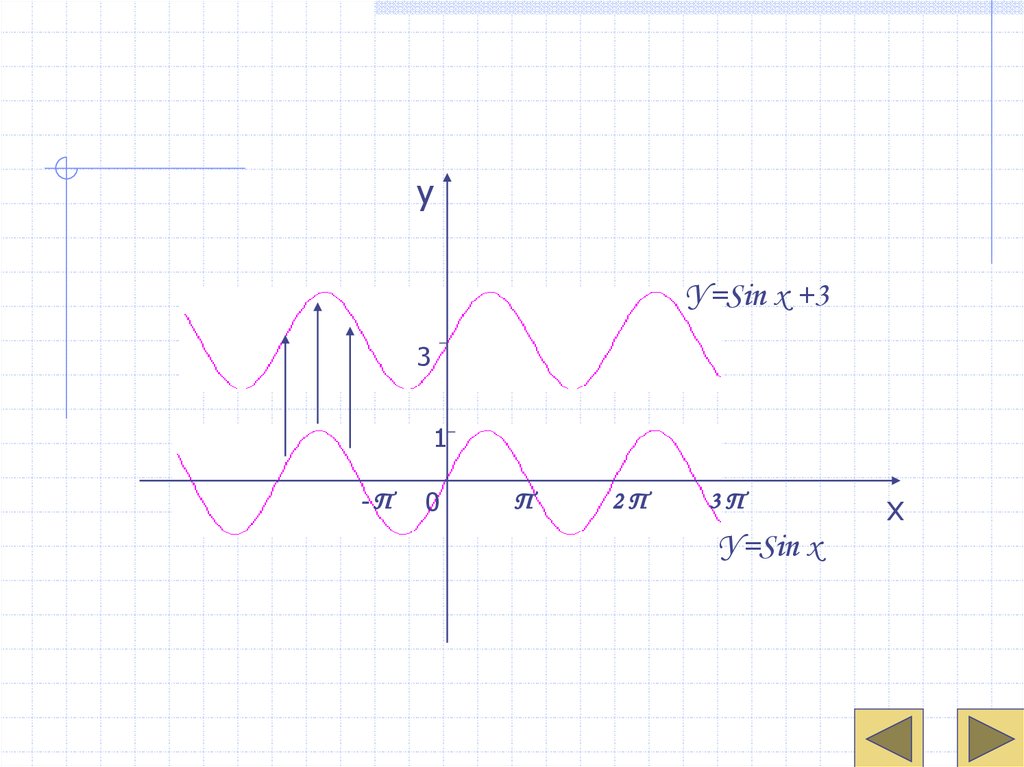
у
У=Sin x +3
3
1
-П
0
П
2П
3П
У=Sin x
х

19.

2
1
-3 П
-2 П
-П
0
-1
П
2П
3П
х