Similar presentations:
Движения. Геометрия. 9 класс
1.
ДВИЖЕНИЯГеометрия 9 класс
2.
Цели :повторить осевую и центральную симметрии;
ввести понятие отображения плоскости на себя
и понятие движения;
научить учащихся осуществлять
параллельный перенос и поворот фигуры;
совершенствовать навыки решения задач
на построение.
3. Содержание
Параллельныйперенос
Симметрия
Отображение
относительно
плоскости
точки
на себя
Понятие
Симметрия
относительно
прямой
движения
Поворот
Самост.
работа
4. Осевая симметрия
Повторение.Центральная симметрия
Дано: точки А и О.
Построить:
точку В, симметричную
точке А относительно
точки О.
А
О
Осевая симметрия
Дано: точки А и прямая
m.
Построить:
точку В, симметричную
точке А относительно
прямой m.
m
А
построение
построение
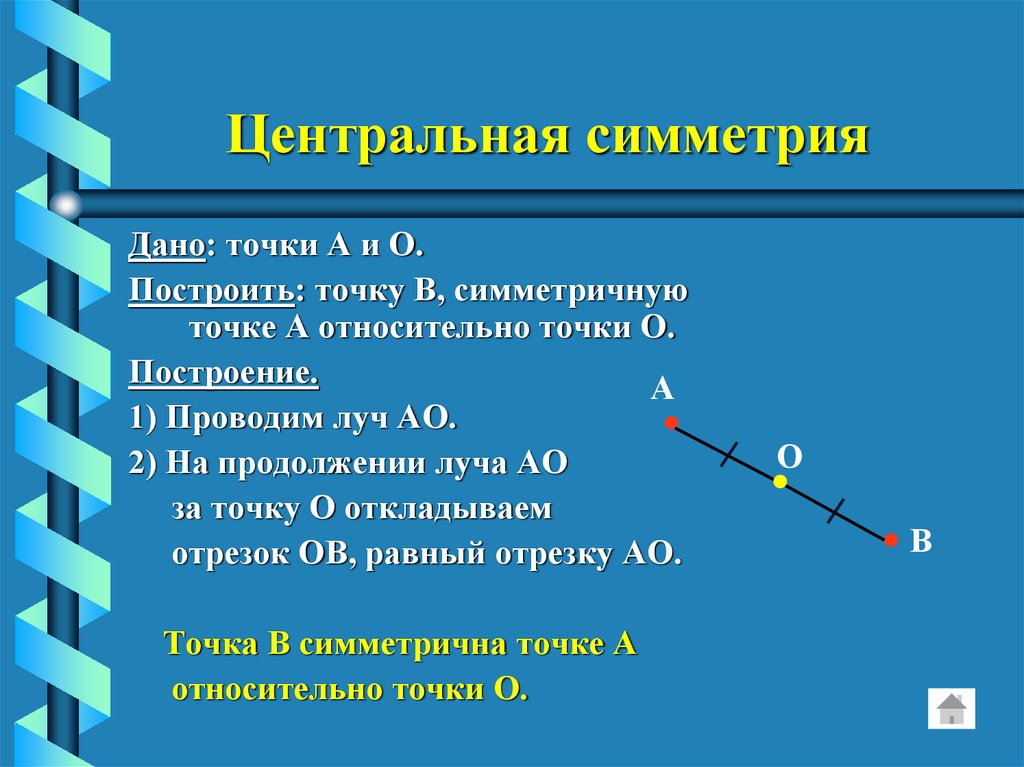
5. Центральная симметрия
Дано: точки А и О.Построить: точку В, симметричную
точке А относительно точки О.
Построение.
А
1) Проводим луч АО.
2) На продолжении луча АО
за точку О откладываем
отрезок ОВ, равный отрезку АО.
Точка В симметрична точке А
относительно точки О.
О
В
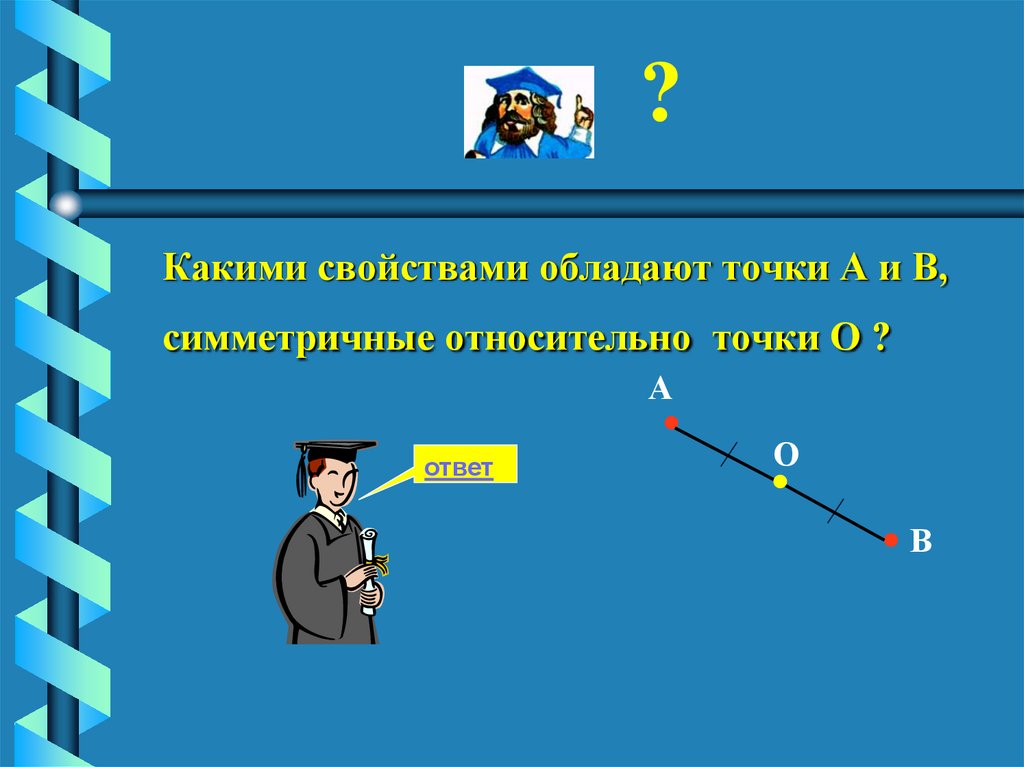
6. Какими свойствами обладают точки А и В, симметричные относительно точки О ?
?Какими свойствами обладают точки А и В,
симметричные относительно точки О ?
А
ответ
О
В
7.
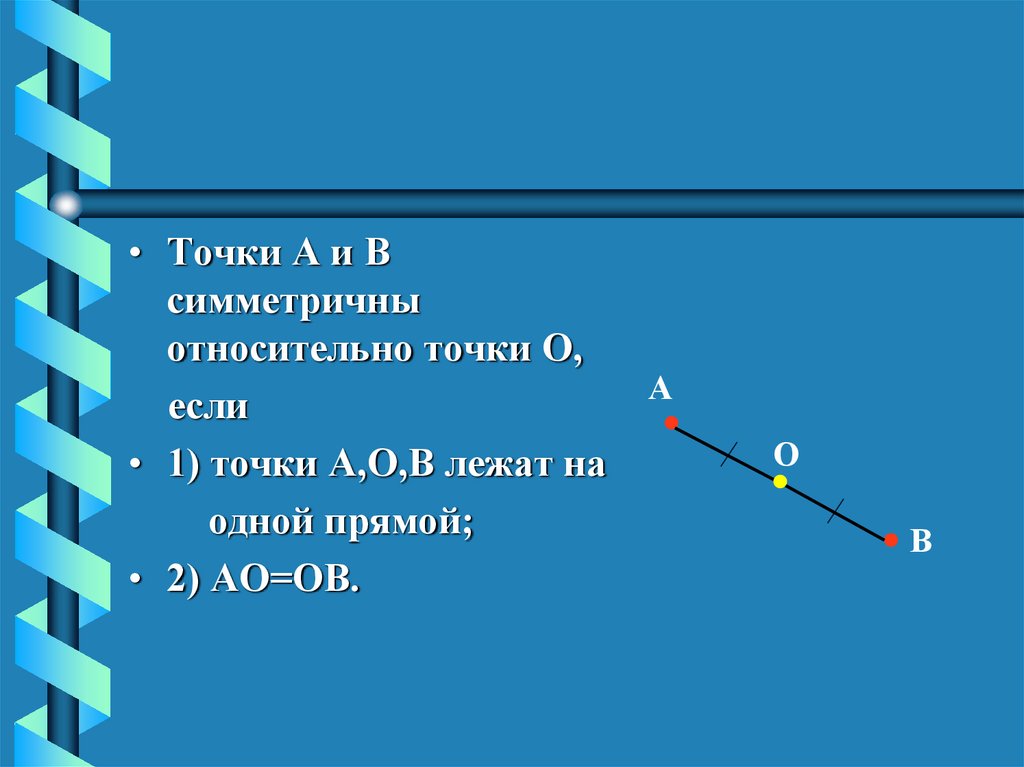
• Точки А и Всимметричны
относительно точки О,
если
• 1) точки А,О,В лежат на
одной прямой;
• 2) АО=ОВ.
А
О
В
8.
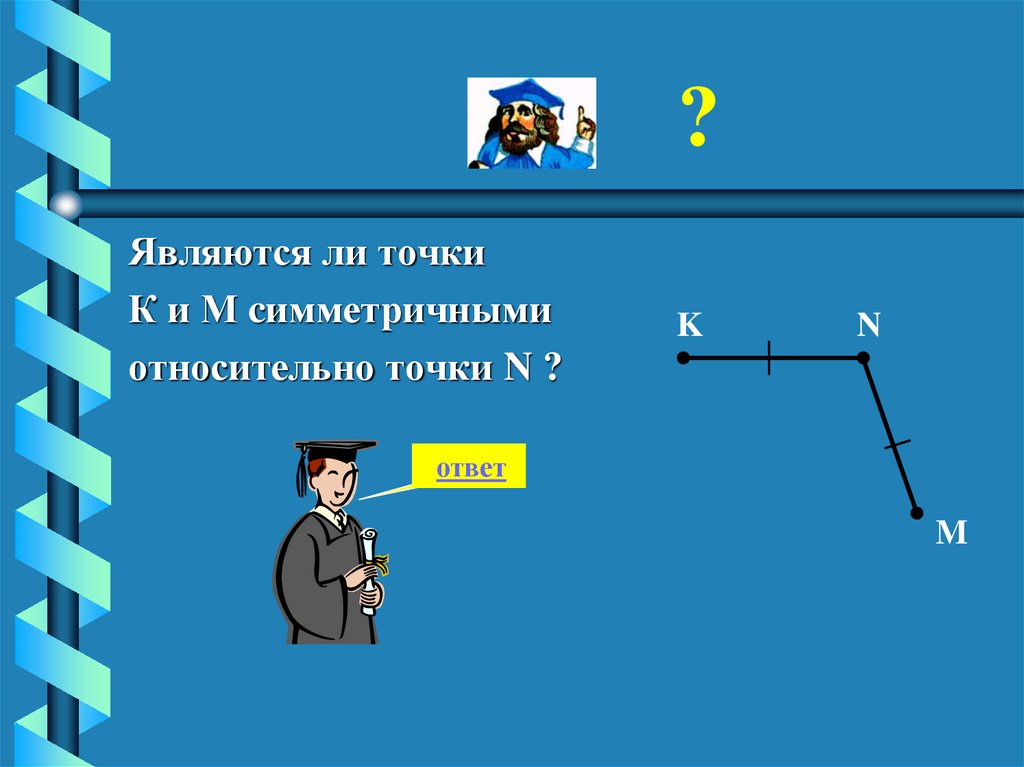
?Являются ли точки
К и М cимметричными
относительно точки N ?
K
N
ответ
M
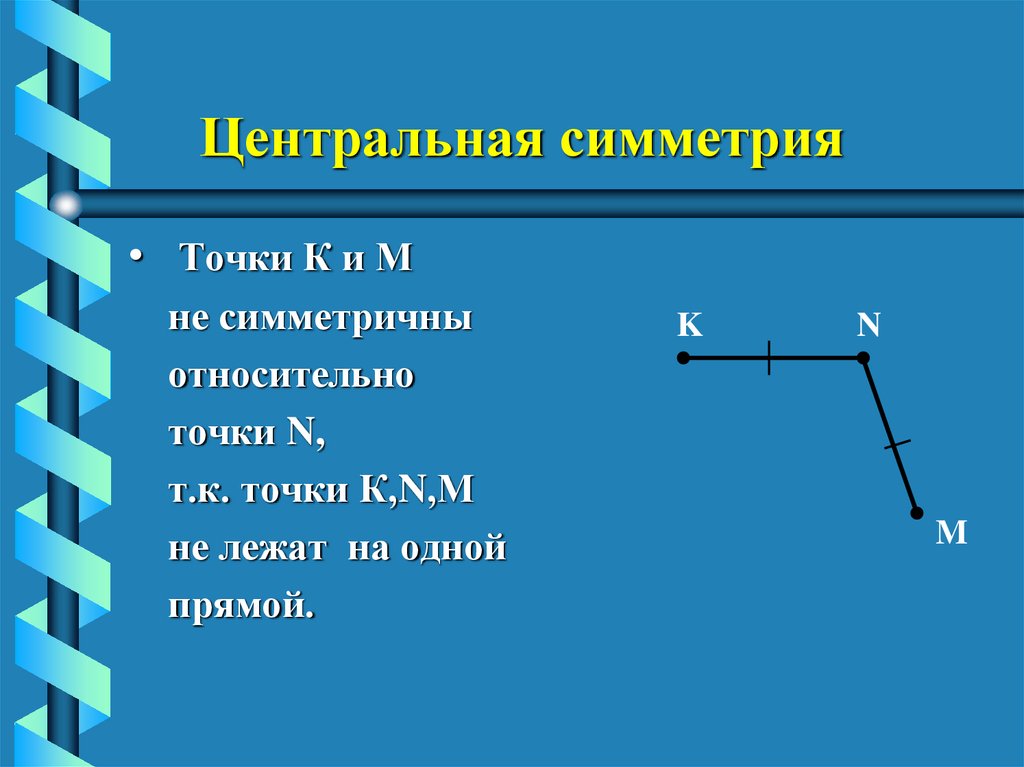
9. Центральная симметрия
• Точки К и Мне симметричны
относительно
точки N,
т.к. точки К,N,М
не лежат на одной
прямой.
K
N
M
10.
?Являются ли точки
А и В симметричными
относительно точки О ?
ответ
А
О
В
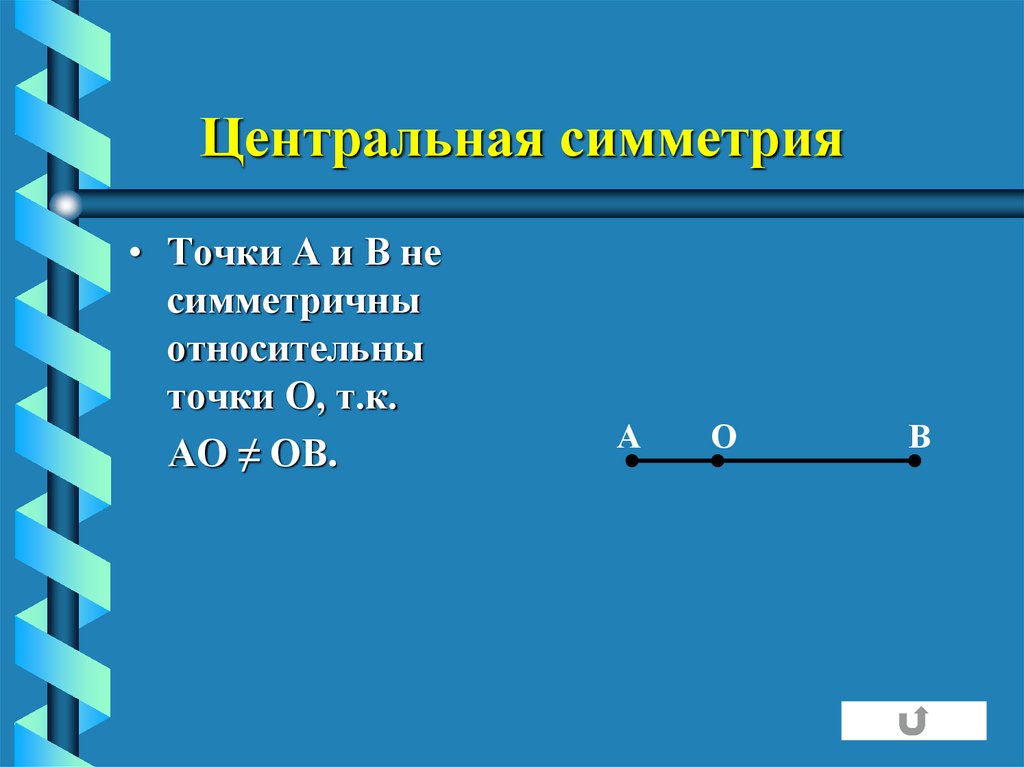
11. Центральная симметрия
• Точки А и В несимметричны
относительны
точки О, т.к.
АО ≠ ОВ.
А
О
В
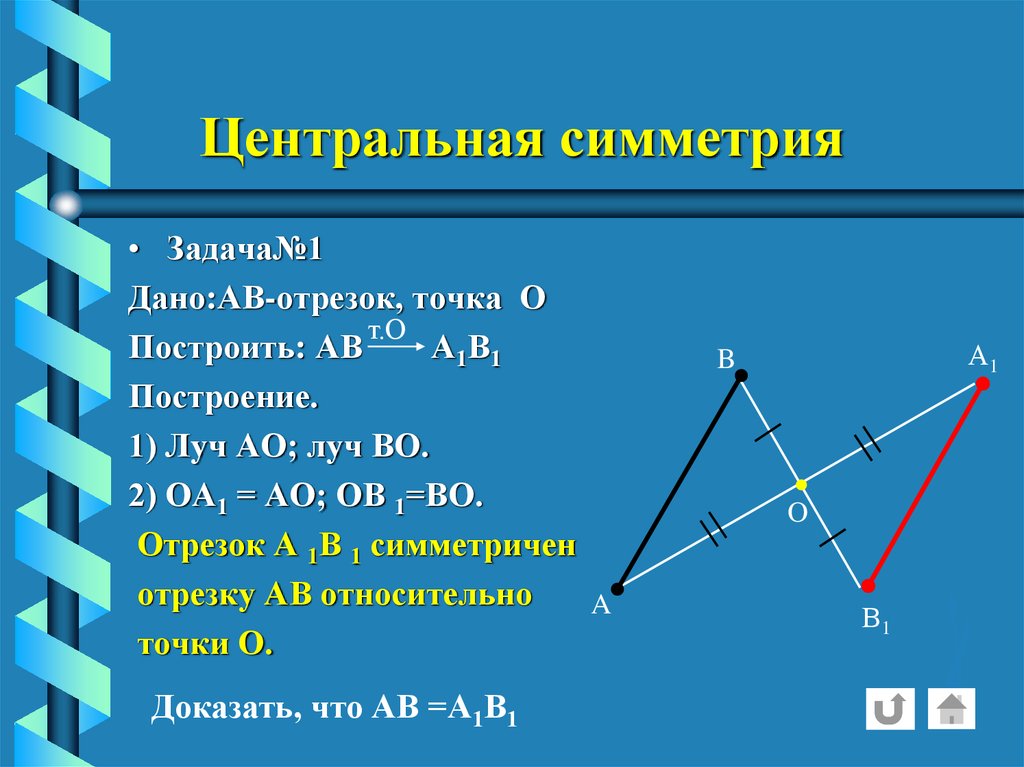
12. Центральная симметрия
• Задача№1Дано:АВ-отрезок, точка О
т.О
Построить: АВ
А1В1
Построение.
1) Луч АО; луч ВО.
2) ОА1 = АО; ОВ 1=ВО.
Отрезок А 1В 1 симметричен
отрезку АВ относительно
A
точки О.
Доказать, что АВ =А1В1
А1
B
O
В1
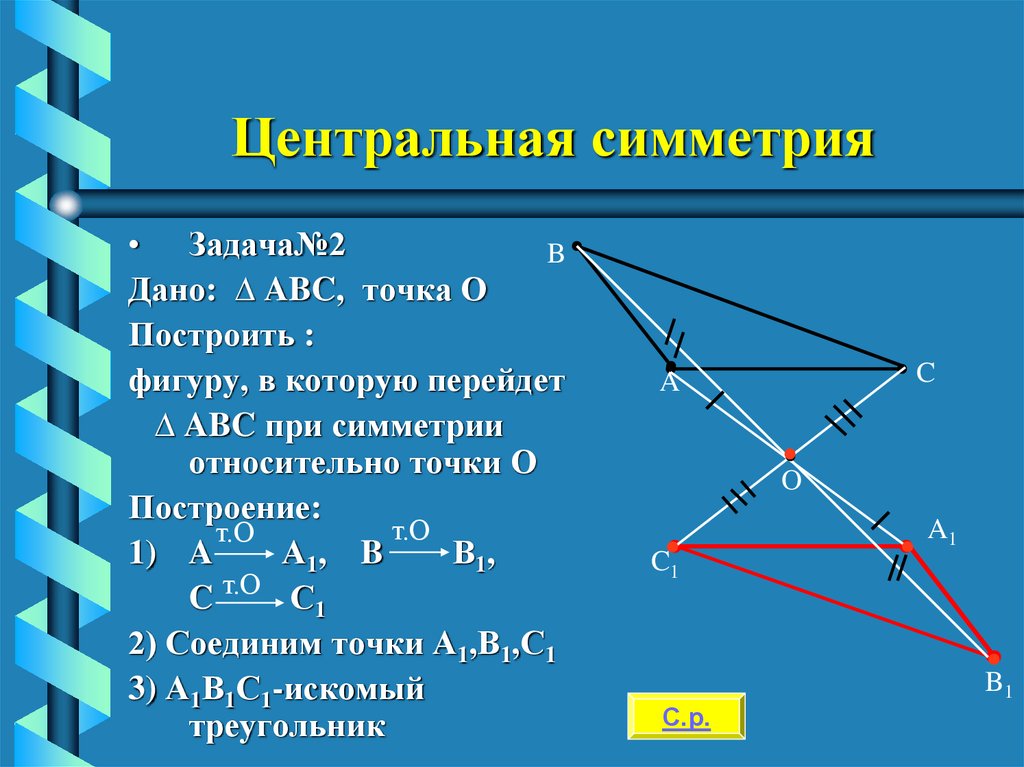
13. Центральная симметрия
• Задача№2B
Дано: ∆ ABC, точка О
Построить :
фигуру, в которую перейдет
∆ ABC при симметрии
относительно точки О
Построение:
т.О
т.О
1) A
А1, B
В1,
C т.О С1
2) Соединим точки А1,В1,С1
3) А1В1С1-искомый
треугольник
C
A
O
A1
C1
B1
С.р.
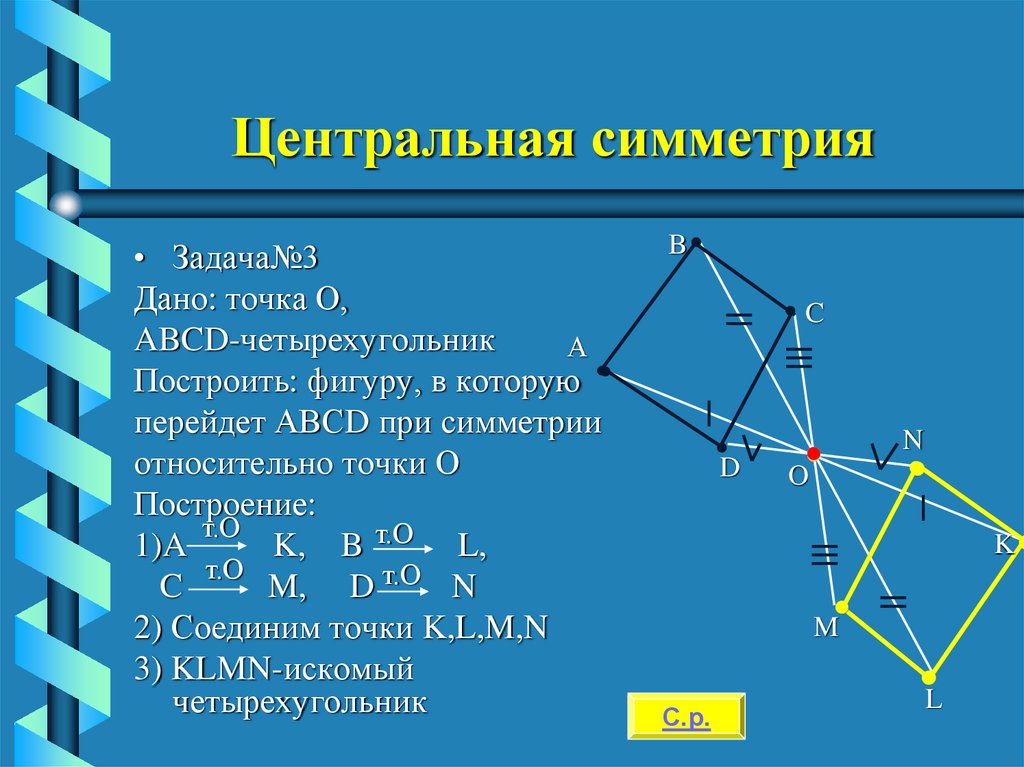
14. Центральная симметрия
• Задача№3Дано: точка О,
ABCD-четырехугольник
А
Построить: фигуру, в которую
перейдет АВСD при симметрии
относительно точки О
Построение:
т.О
1)A
K, B т.О L,
т.О
C
M, D т.О N
2) Соединим точки K,L,M,N
3) KLMN-искомый
четырехугольник
B
C
N
D
O
K
M
С.р.
L
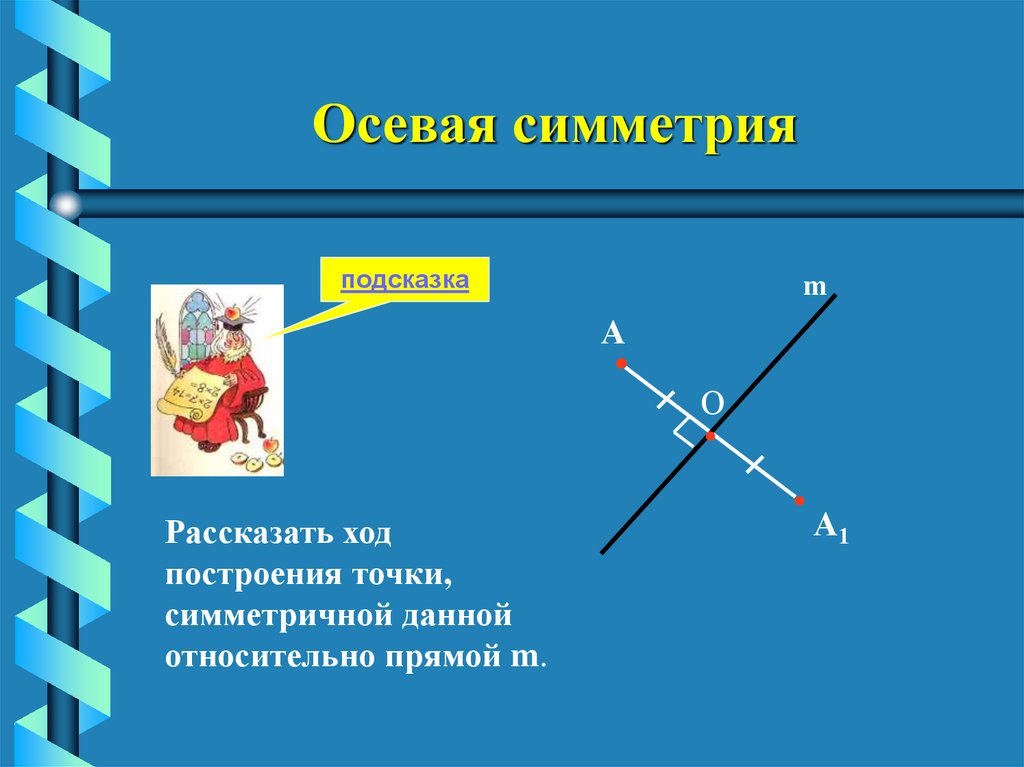
15.
Осевая симметрияподсказка
m
А
О
Рассказать ход
построения точки,
симметричной данной
относительно прямой m.
А1
16.
Осевая симметрияДано: точка А, прямая m.
Построить : точку В,
симметричную точке А
А
относительно точки О.
Построение.
1) Из точки А опустить
перпендикуляр к прямой m,
АО m.
2) На продолжении
перпендикуляра за точку О
отложить отрезок ОВ,
равный отрезку АО.
m
О
В
С.р.
17.
?Какими свойствами
обладают точки А и В,
симметричные
относительно прямой m ?
ответ
m
А
О
В
18.
Осевая симметрияТочки А и В
симметричны
относительно прямой m,
если
1) точки А,О,В лежат на
одной прямой,
перпендикулярной
прямой m;
2) АО=ОВ.
m
А
О
А1
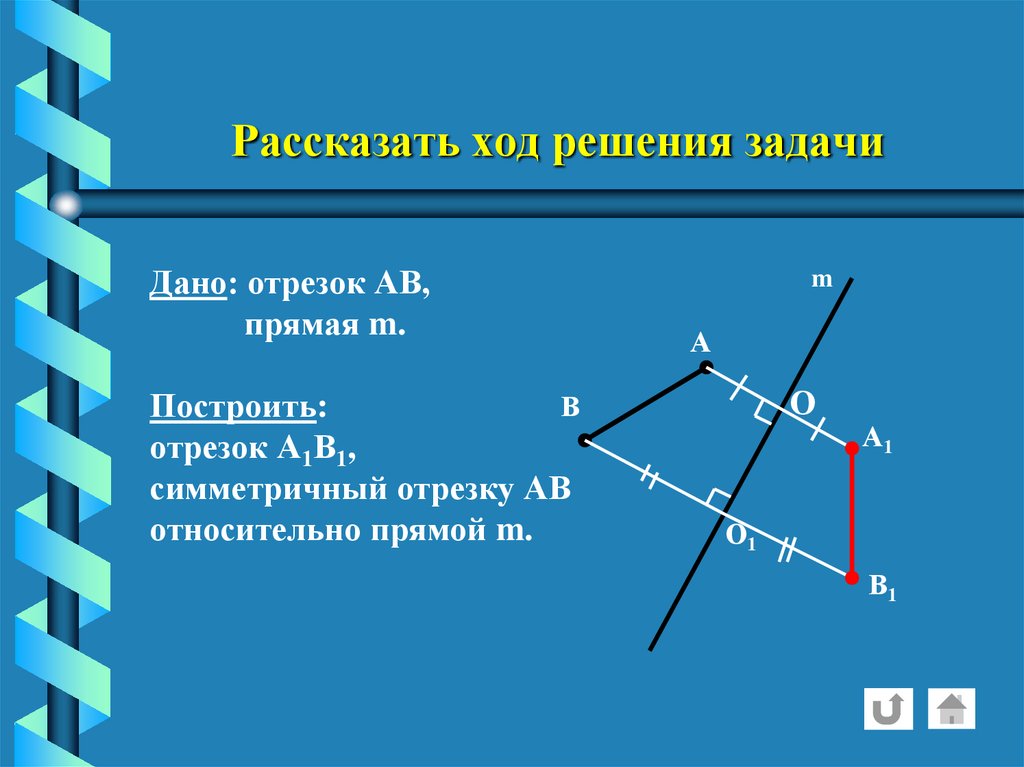
19. Рассказать ход решения задачи
Дано: отрезок АВ,прямая m.
В
Построить:
отрезок А1В1,
симметричный отрезку АВ
относительно прямой m.
m
А
О
А1
О1
В1
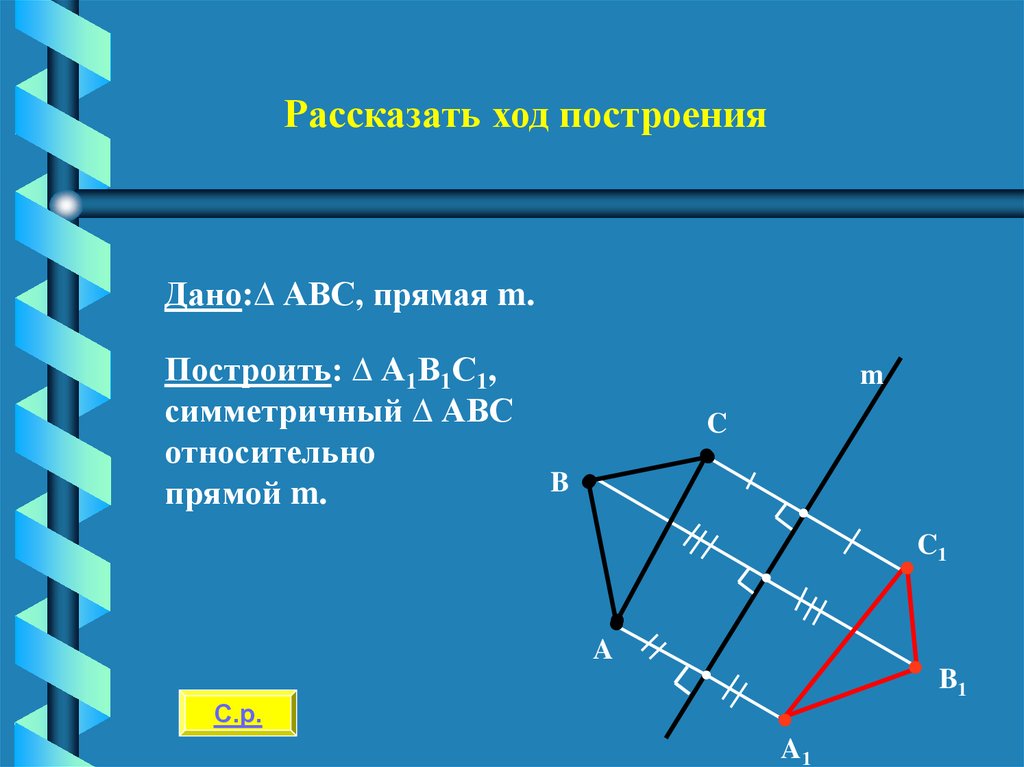
20.
Рассказать ход построенияДано:∆ АВС, прямая m.
Построить: ∆ А1В1С1,
симметричный ∆ АВС
относительно
прямой m.
m
C
B
C1
A
B1
С.р.
A1
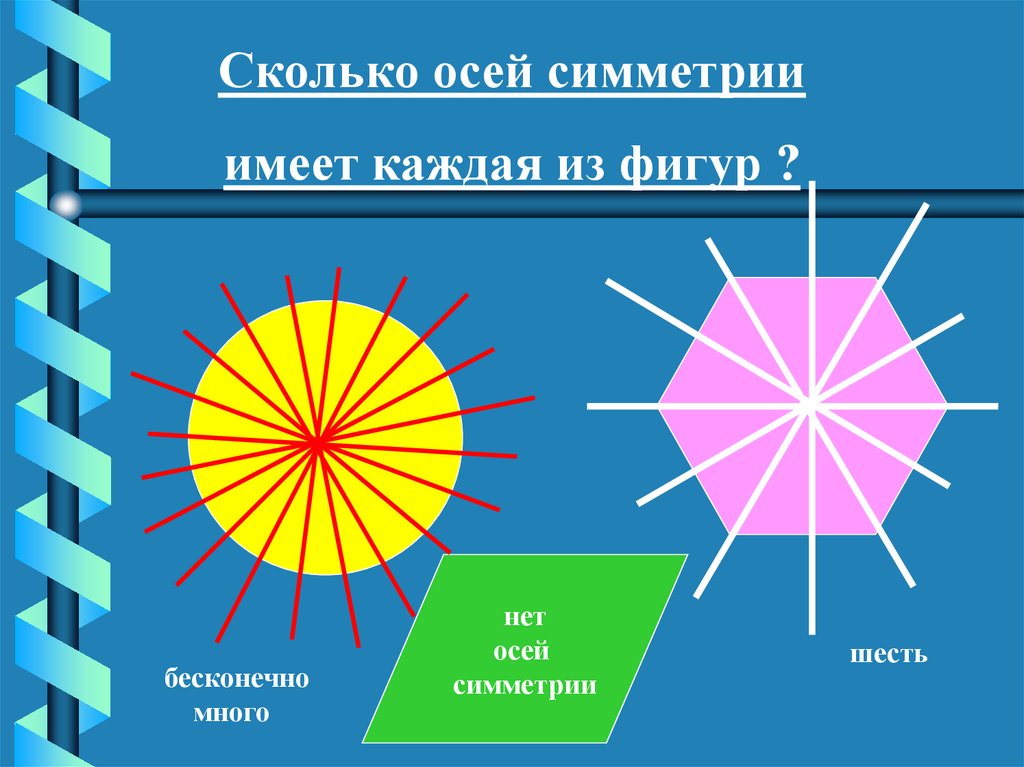
21.
Сколько осей симметрииимеет каждая из фигур ?
бесконечно
много
нет
осей
симметрии
шесть
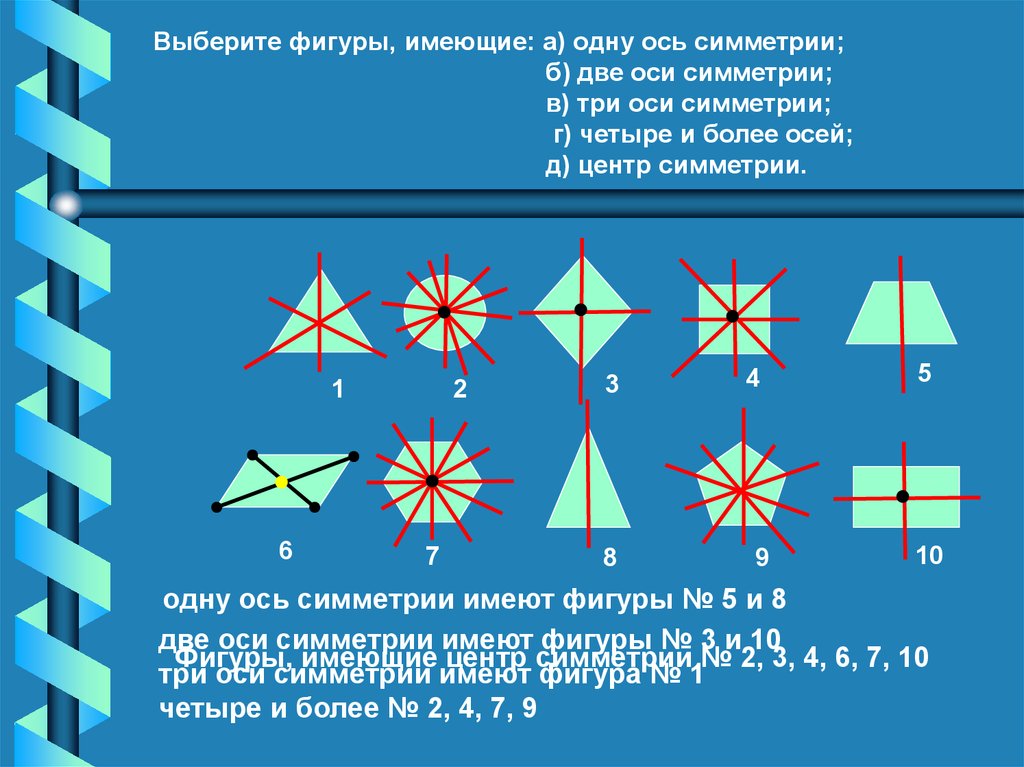
22.
Выберите фигуры, имеющие: а) одну ось симметрии;б) две оси симметрии;
в) три оси симметрии;
г) четыре и более осей;
д) центр симметрии.
1
6
2
7
3
4
5
8
9
10
одну ось симметрии имеют фигуры № 5 и 8
две оси симметрии имеют фигуры № 3 и 10
Фигуры, имеющие центр симметрии № 2, 3, 4, 6, 7, 10
три оси симметрии имеют фигура № 1
четыре и более № 2, 4, 7, 9
23.
24.
25.
26.
27.
28.
29.
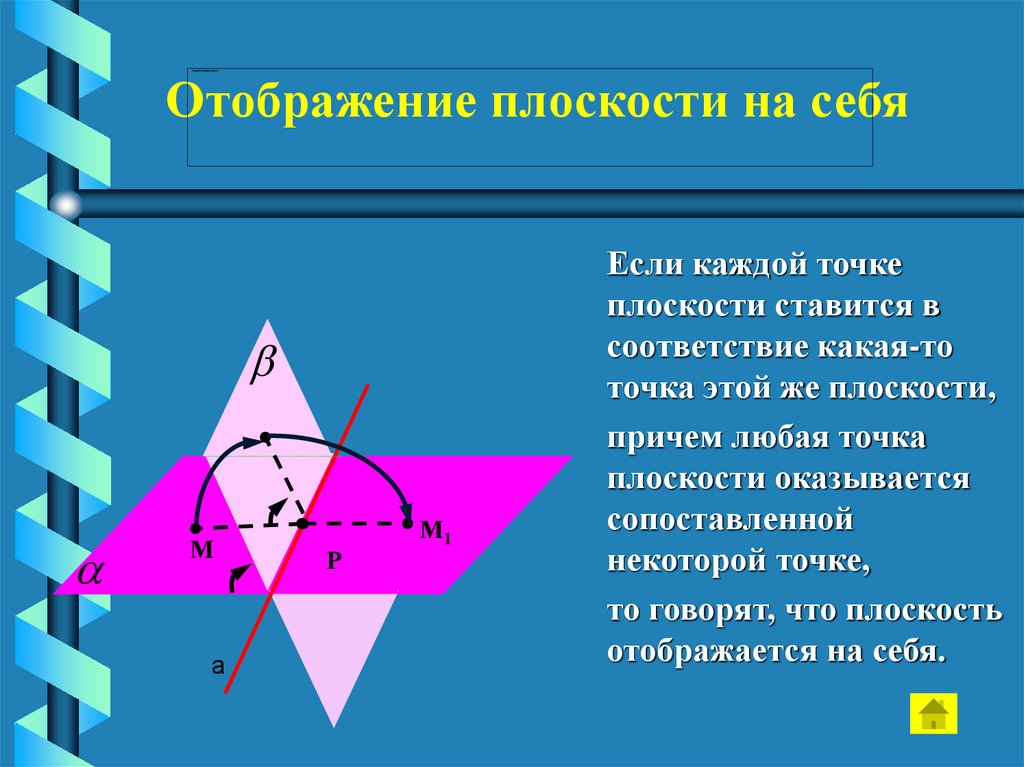
Отображение плоскости на себяМ
a
Р
М1
Если каждой точке
плоскости ставится в
соответствие какая-то
точка этой же плоскости,
причем любая точка
плоскости оказывается
сопоставленной
некоторой точке,
то говорят, что плоскость
отображается на себя.
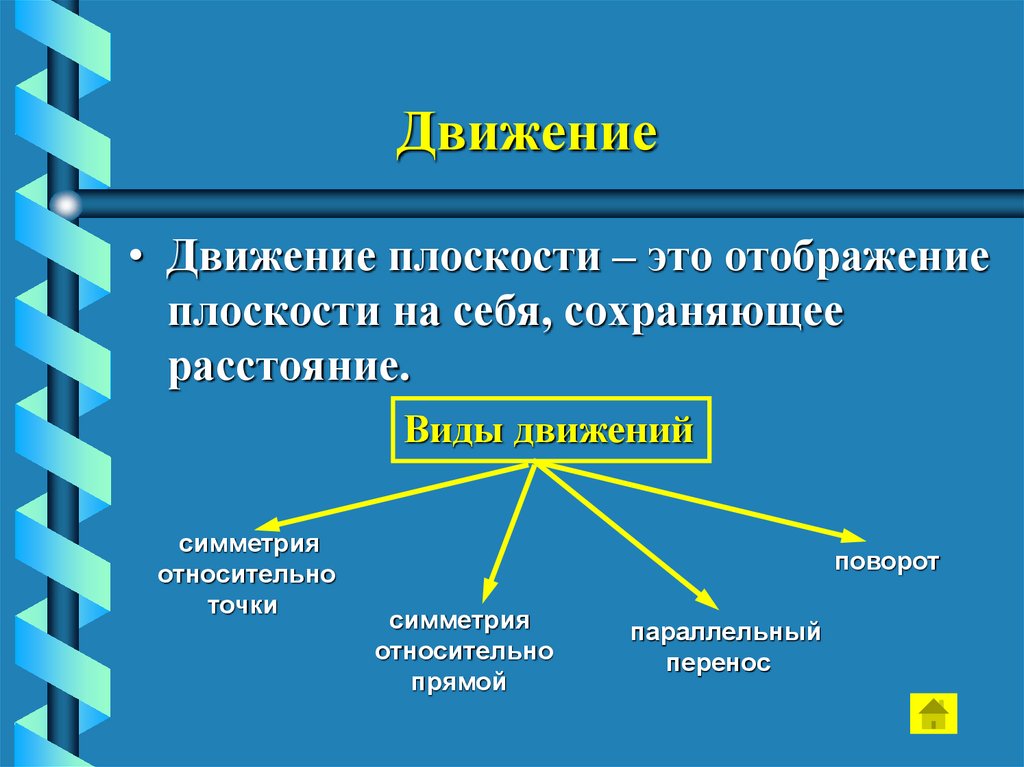
30. Движение
• Движение плоскости – это отображениеплоскости на себя, сохраняющее
расстояние.
Виды движений
симметрия
относительно
точки
поворот
симметрия
относительно
прямой
параллельный
перенос
31.
Параллельный переносПараллельным переносом на вектор a
называется отображение плоскости
на себя, при котором каждая точка М
отображается в такую точку
N,
что
равен вектору a
N
М
a
32.
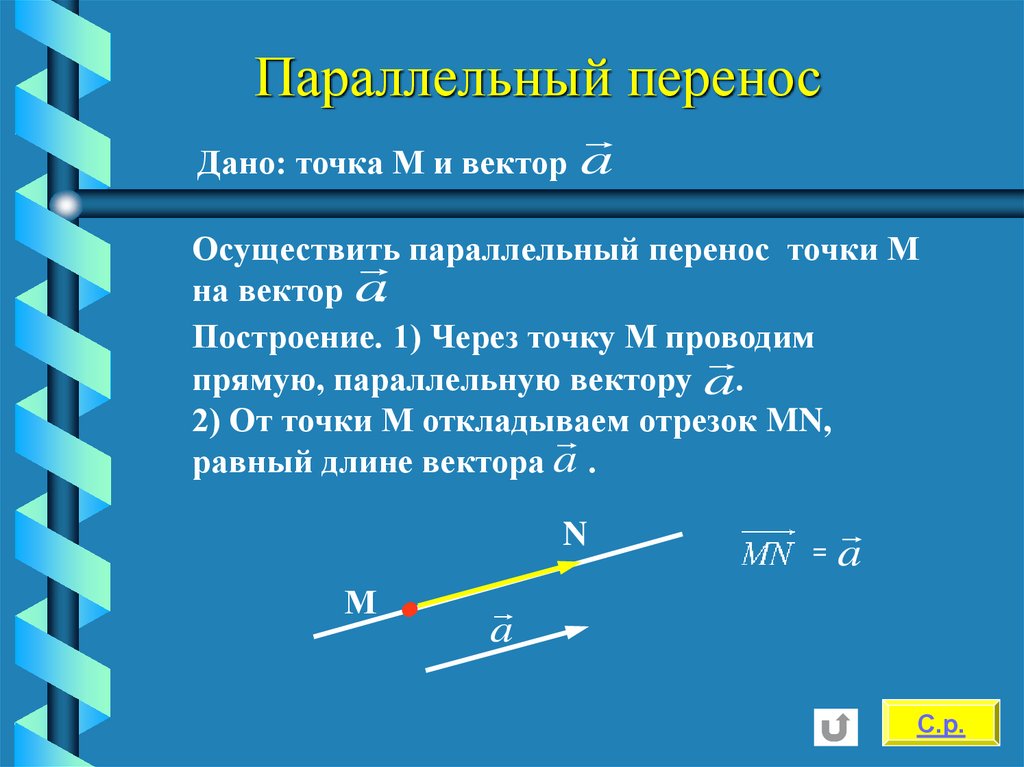
Параллельный переносДано: точка М и вектор a
Осуществить
параллельный перенос точки М
на вектор a.
Построение. 1) Через точку М проводим
прямую, параллельную вектору a.
2) От точки М откладываем
отрезок MN,
равный длине вектора a .
N
М
= a
a
С.р.
33.
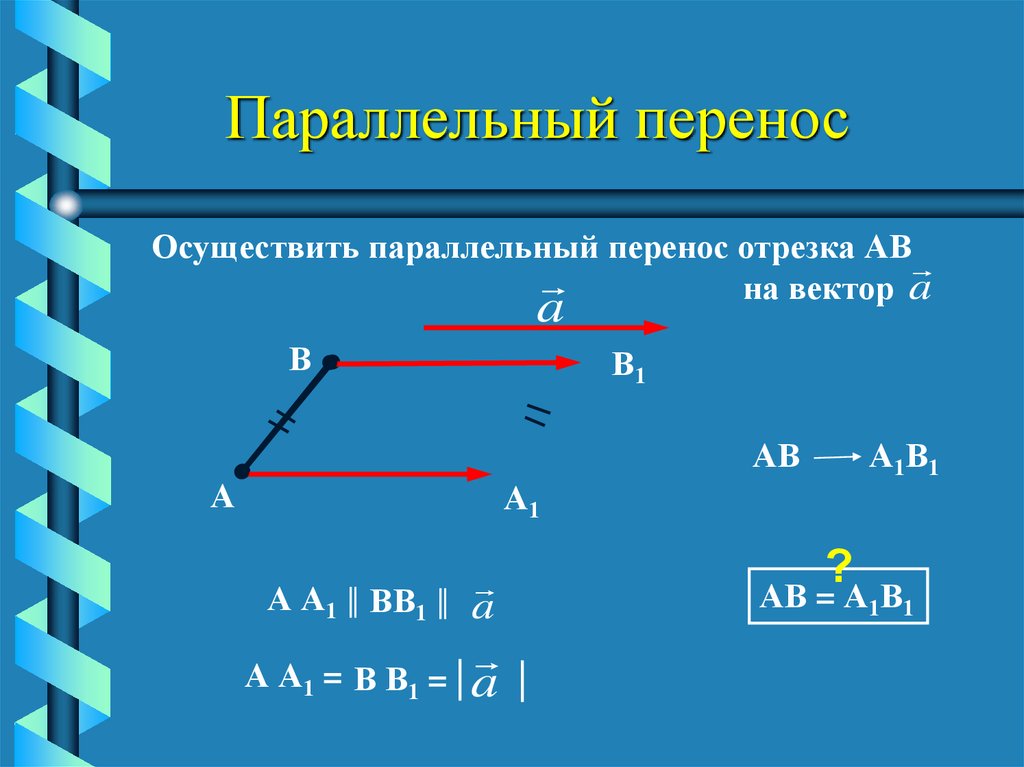
Параллельный переносОсуществить параллельный перенос отрезка АВ
на вектор a
a
В
В1
А1В1
АВ
А
А1
А А1 ║ ВВ1 ║ a
А А1 = В В1 =│a │
?
АВ = А1В1
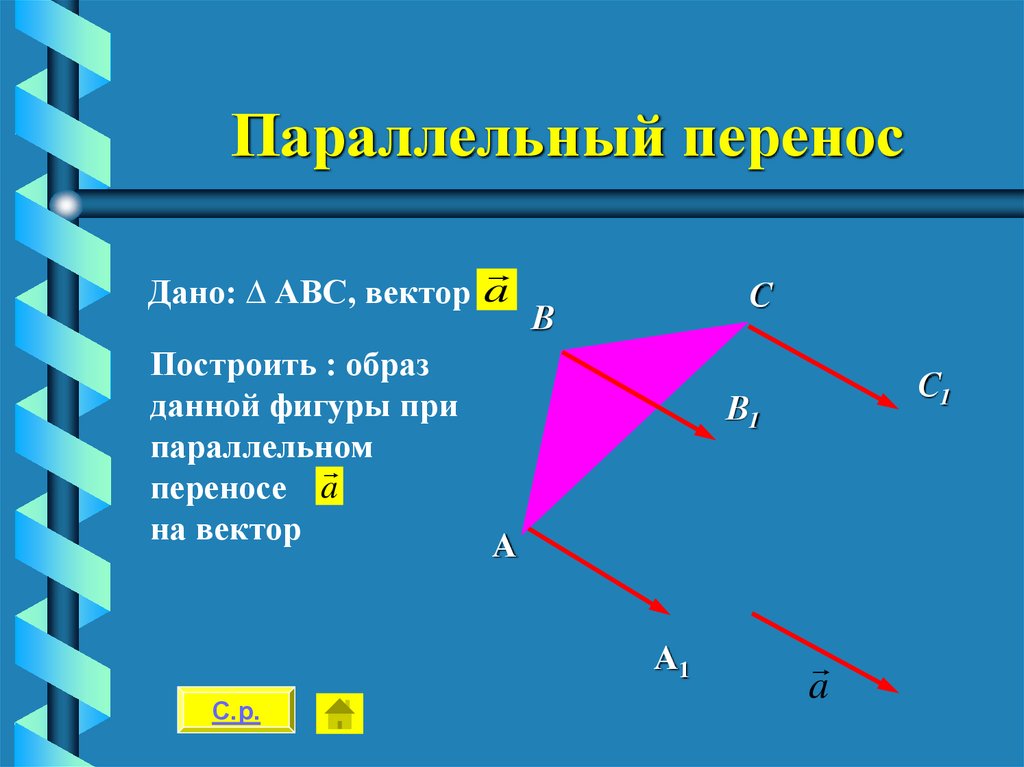
34. Параллельный перенос
Дано: ∆ АВС, вектор aС
В
Построить : образ
данной фигуры при
параллельном
переносе a
на вектор
А
В1
А1
С.р.
С1
a
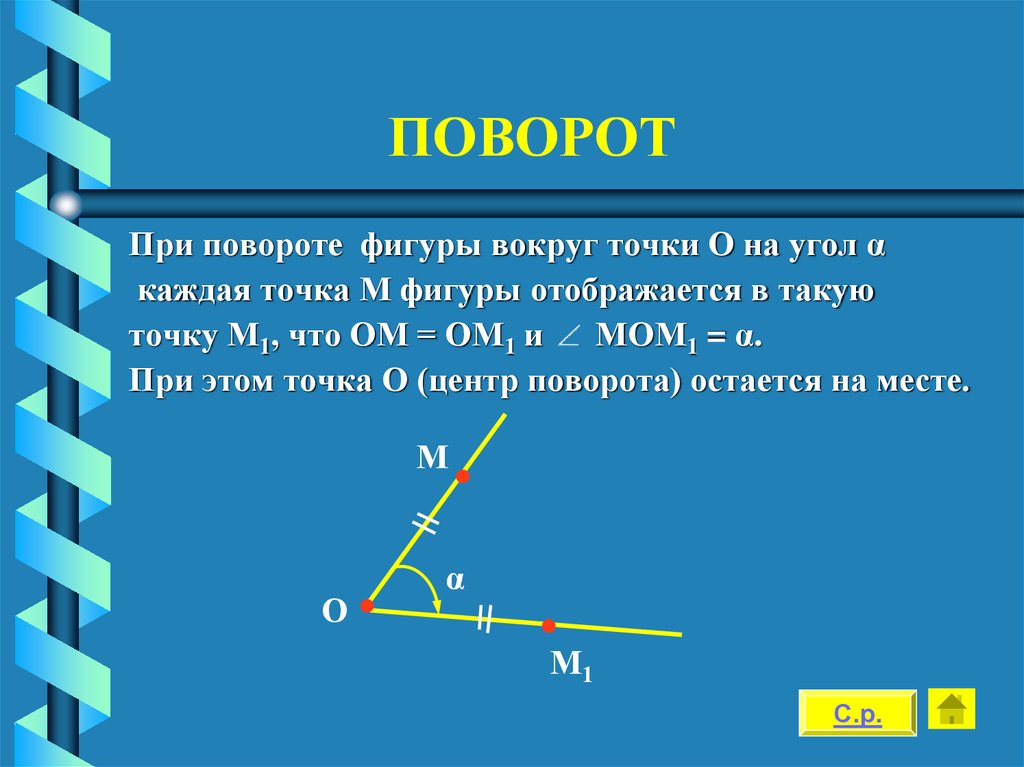
35. ПОВОРОТ
При повороте фигуры вокруг точки О на угол αкаждая точка М фигуры отображается в такую
точку М1, что ОМ = ОМ1 и
МОМ1 = α.
При этом точка О (центр поворота) остается на месте.
М
О
α
М1
С.р.
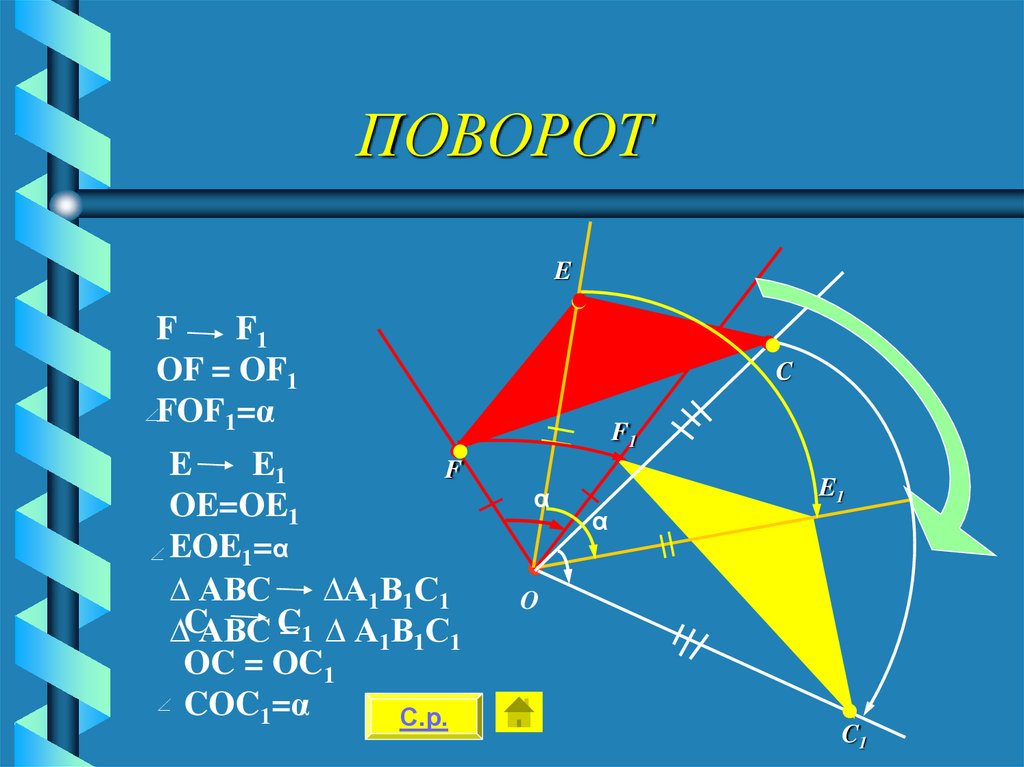
36. ПОВОРОТ
EF
F1
OF = OF1
FOF1=α
E
E1
F
OE=OE1
EOE1=α
∆ АВС
∆А1В1С1
∆CАВС C
= 1 ∆ А1В1С1
OC = OC1
COC =α
1
С.р.
F1
α
E1
α
O
C1
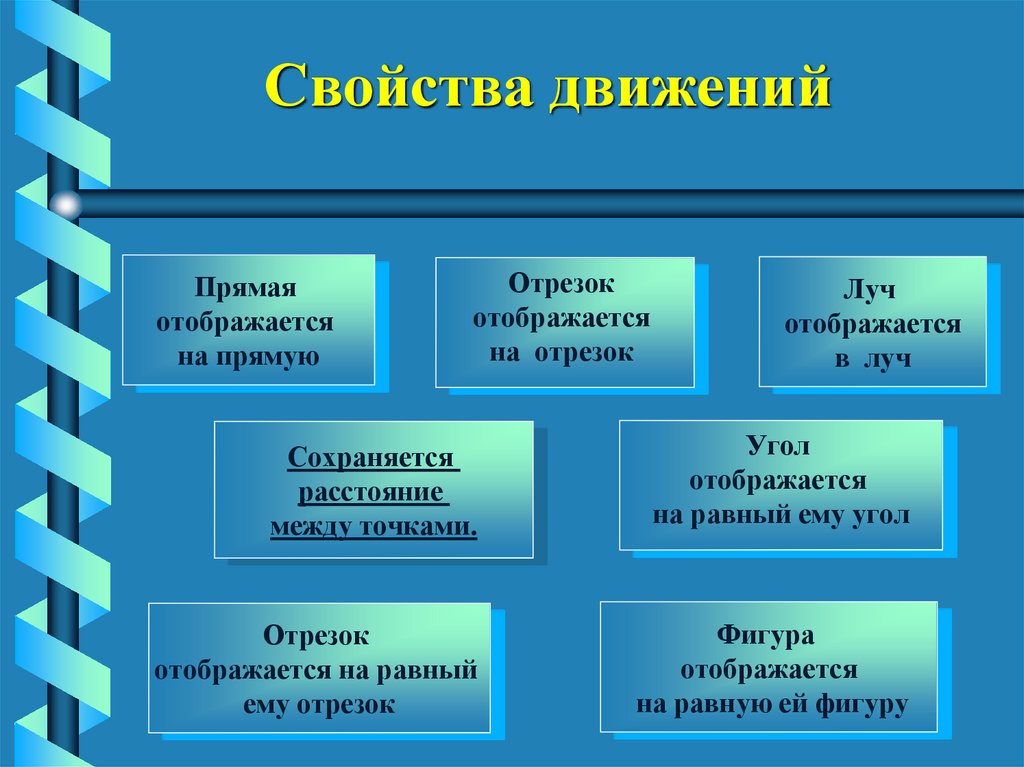
37.
Свойства движенийПрямая
отображается
на прямую
Отрезок
отображается
на отрезок
Луч
отображается
в луч
Сохраняется
расстояние
между точками.
Угол
отображается
на равный ему угол
Отрезок
отображается на равный
ему отрезок
Фигура
отображается
на равную ей фигуру
38. Самостоятельная работа
Вариант №1 Дано: треугольник АВСВариант №2 Дано: четырехугольник АВСК
Построить:
1) фигуру, симметричную данной относительно точки О;
2) фигуру, симметричную данной относительно
прямой n;
3) образ данной фигуры при параллельном переносе
на вектор а;
4) образ данной фигуры при повороте вокруг точки О
на 75º против часовой стрелки
( на 80º по часовой стрелке).
















 mathematics
mathematics








