Цилиндр и конус. Усеченный конус. Решение задач

1.

«Цилиндр и конус.
Усеченный конус.
Решение задач »

2. Окружность -

Окружностью называется
геометрическая фигура,состоящая из всех
точек плоскости, расположенных на
заданном расстоянии от данной точки
Треугольник -
Геометрическая фигура, состоящая из
трех точек, не лежащих на одной
прямой, и соединяющих их отрезков

3. Примеры цилиндров

Слово цилиндр означает от
греческого слова
“валик”, “каток”.

4. Конусные фигуры в быту

Формы конуса в профессии
«Повара, кондитера»

5.

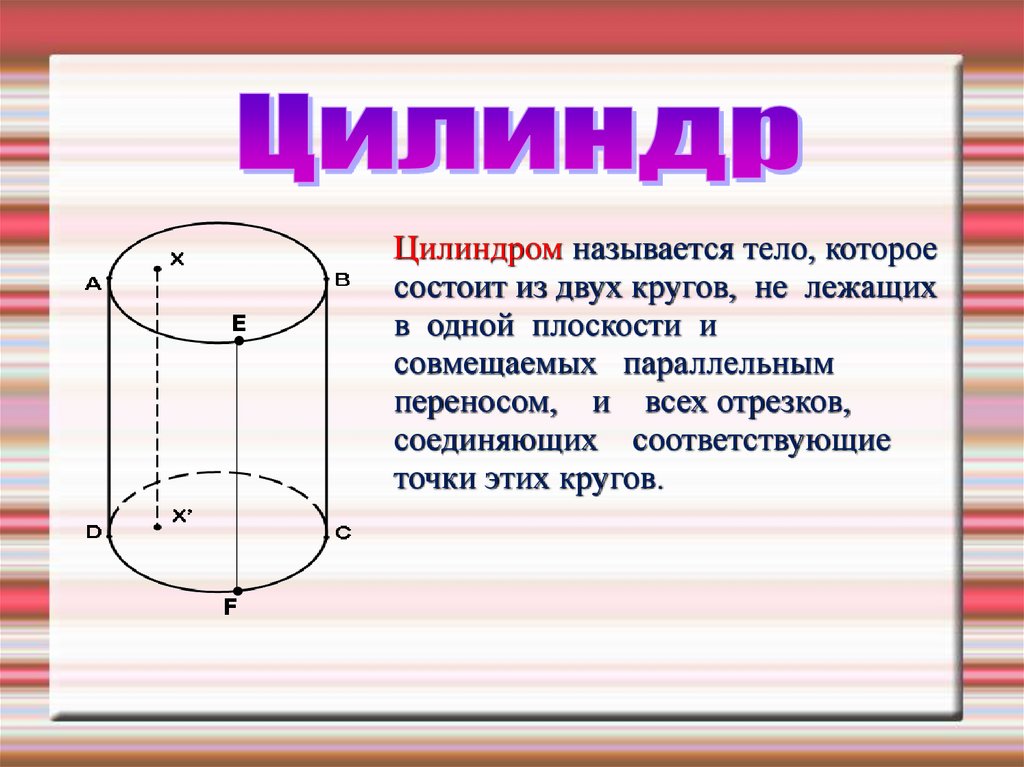
E
F
Цилиндром называется тело, которое
состоит из двух кругов, не лежащих
в одной плоскости и
совмещаемых параллельным
переносом, и всех отрезков,
соединяющих соответствующие
точки этих кругов.

6.

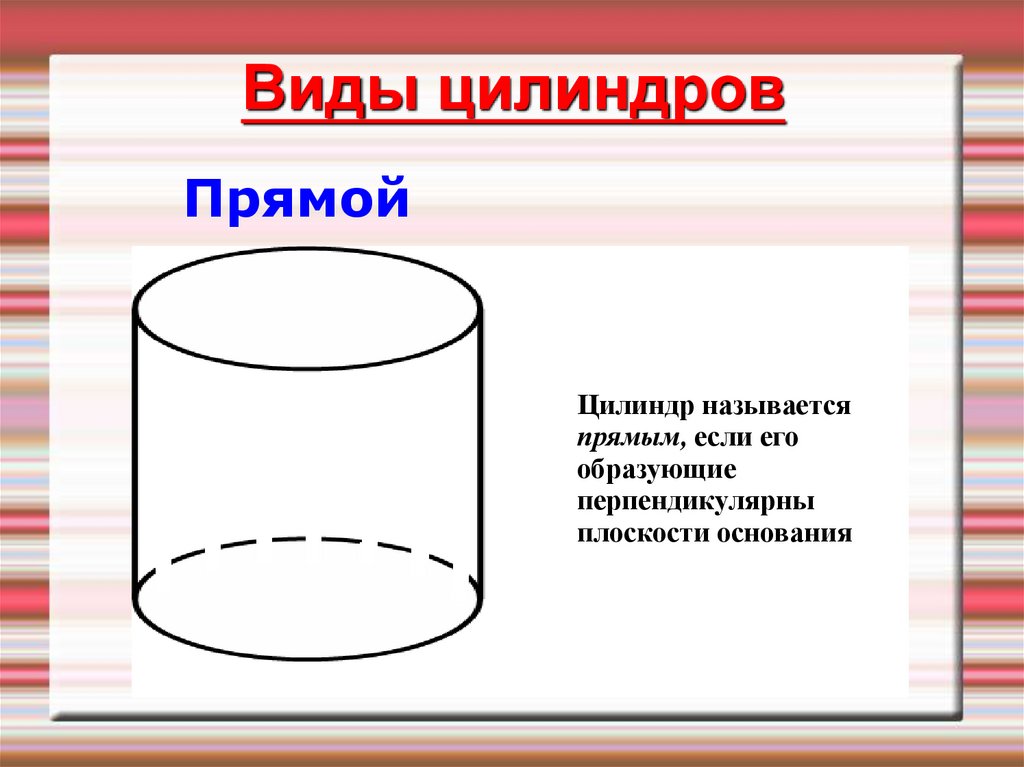
Виды цилиндров
Прямой
Цилиндр называется
прямым, если его
образующие
перпендикулярны
плоскости основания

7.

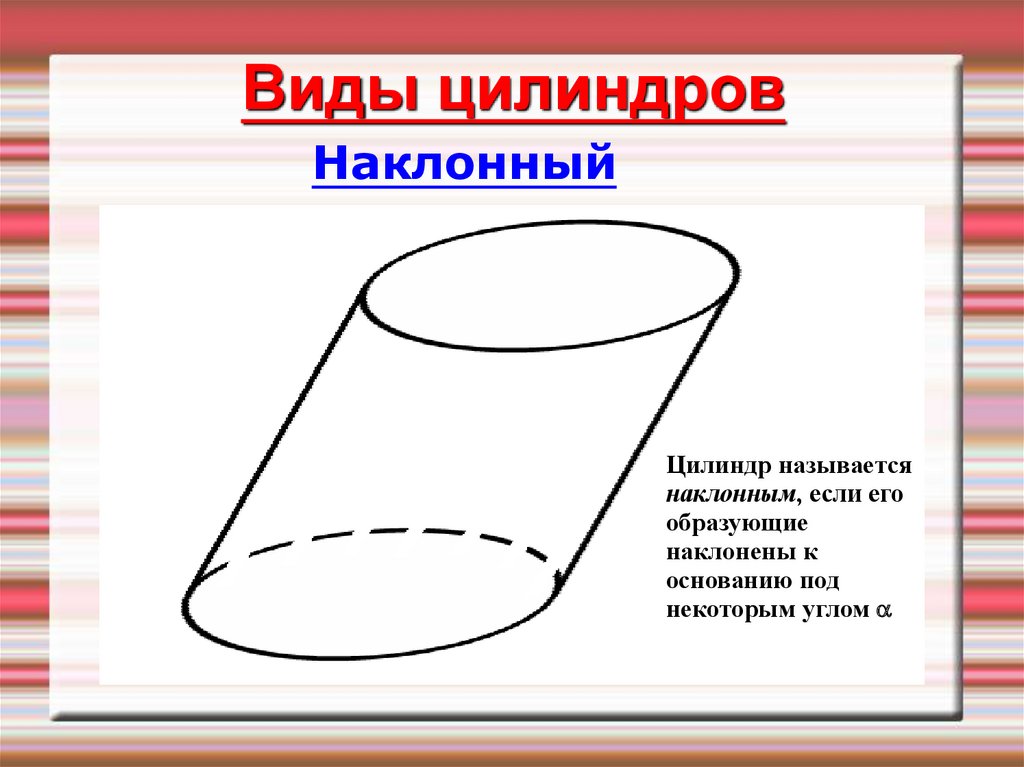
Виды цилиндров
Наклонный
Цилиндр называется
наклонным, если его
образующие
наклонены к
основанию под
некоторым углом

8.

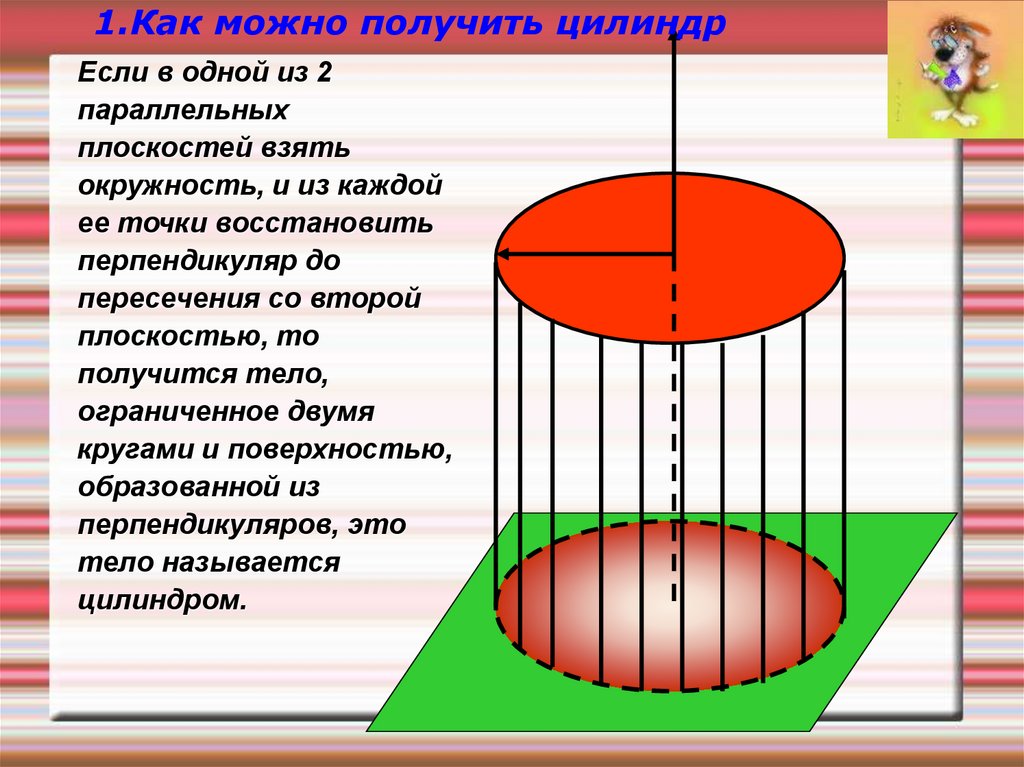
1.Как можно получить цилиндр
Если в одной из 2
параллельных
плоскостей взять
окружность, и из каждой
ее точки восстановить
перпендикуляр до
пересечения со второй
плоскостью, то
получится тело,
ограниченное двумя
кругами и поверхностью,
образованной из
перпендикуляров, это
тело называется
цилиндром.

9.

Круги, лежащие в
параллельных плоскостях,
называются основаниями
цилиндра, а отрезки,
соединяющие
соответствующие точки
окружностей оснований –
называются образующими
цилиндра.
А можно так
получить цилиндр
Вращением
прямоугольника
вокруг одной из
его сторон

10.

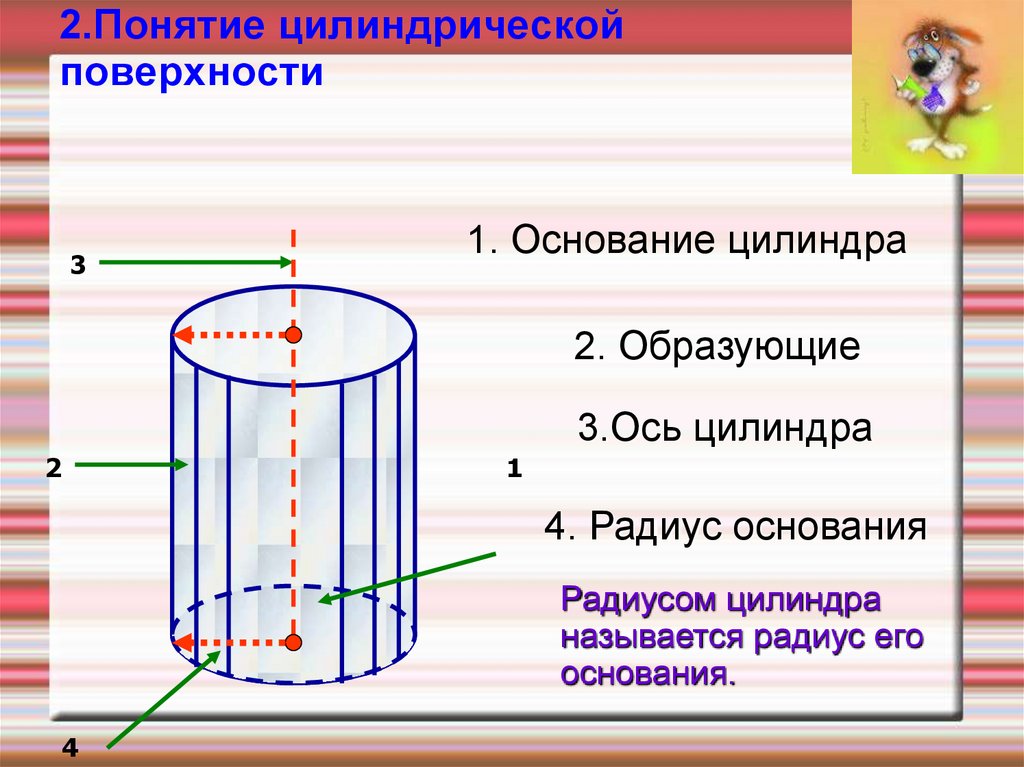
2.Понятие цилиндрической
поверхности
1. Основание цилиндра
3
4
2. Образующие
3.Ось цилиндра
2
1
4. Радиус основания
Радиусом цилиндра
называется радиус его
основания.
4

11.

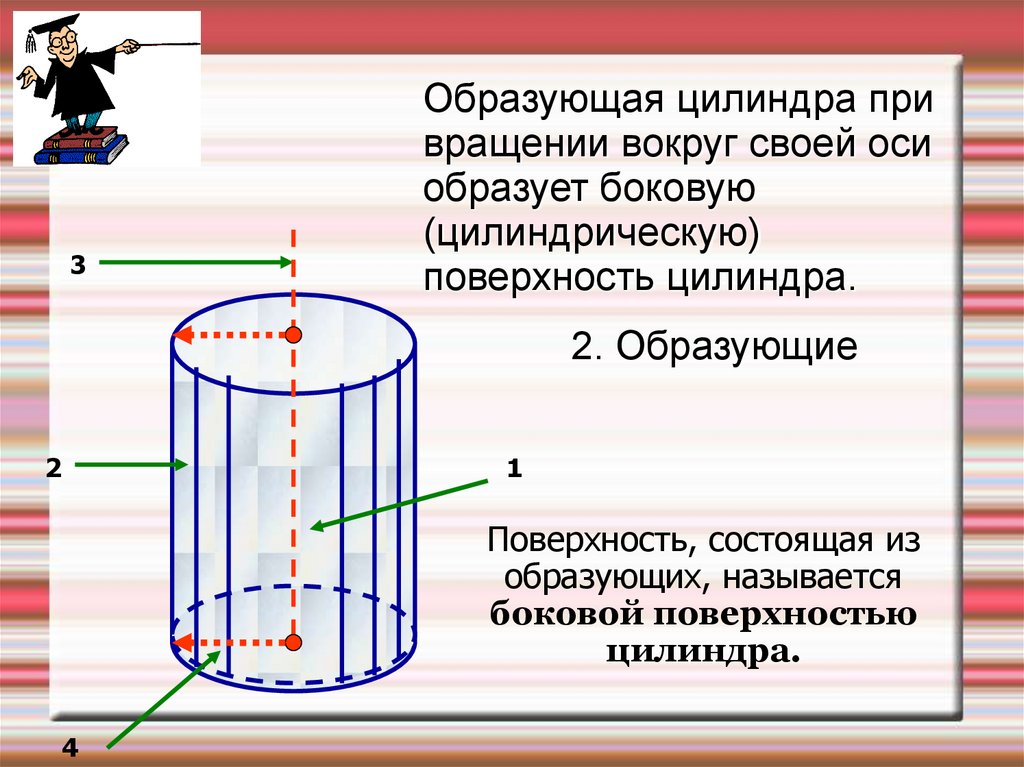
Образующая цилиндра при
вращении вокруг своей оси
образует боковую
(цилиндрическую)
поверхность цилиндра.
3
4
2
2. Образующие
1
Поверхность, состоящая из
образующих, называется
боковой поверхностью
цилиндра.
4

12. Понятие цилиндрической поверхности, цилиндра

13.

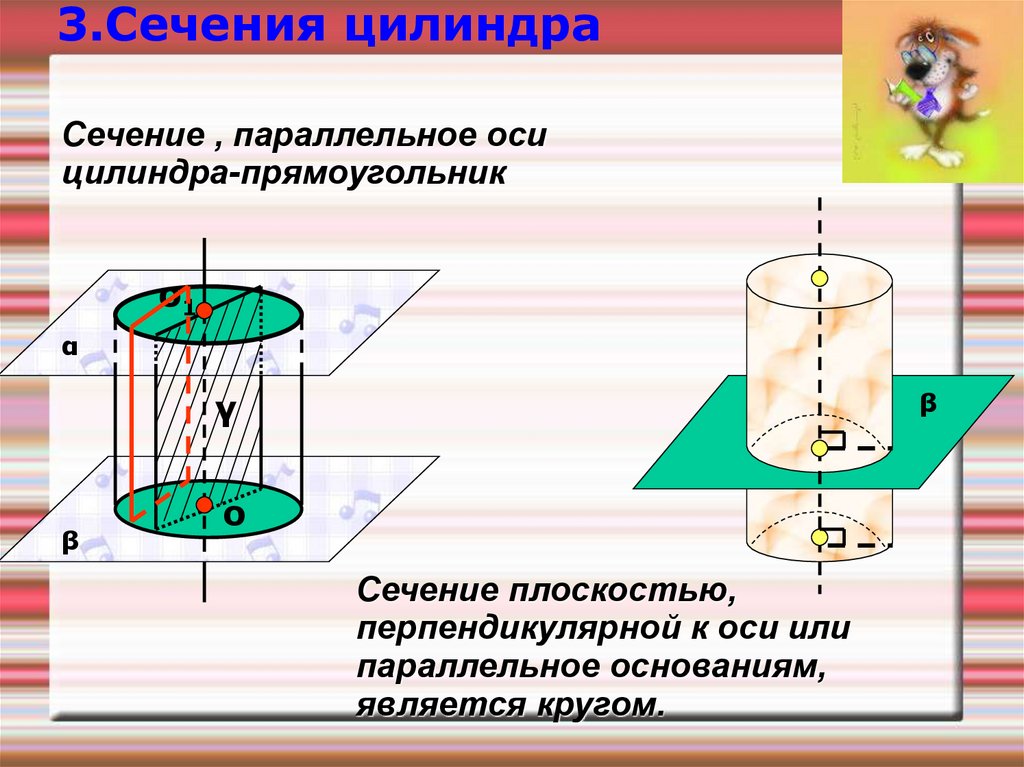
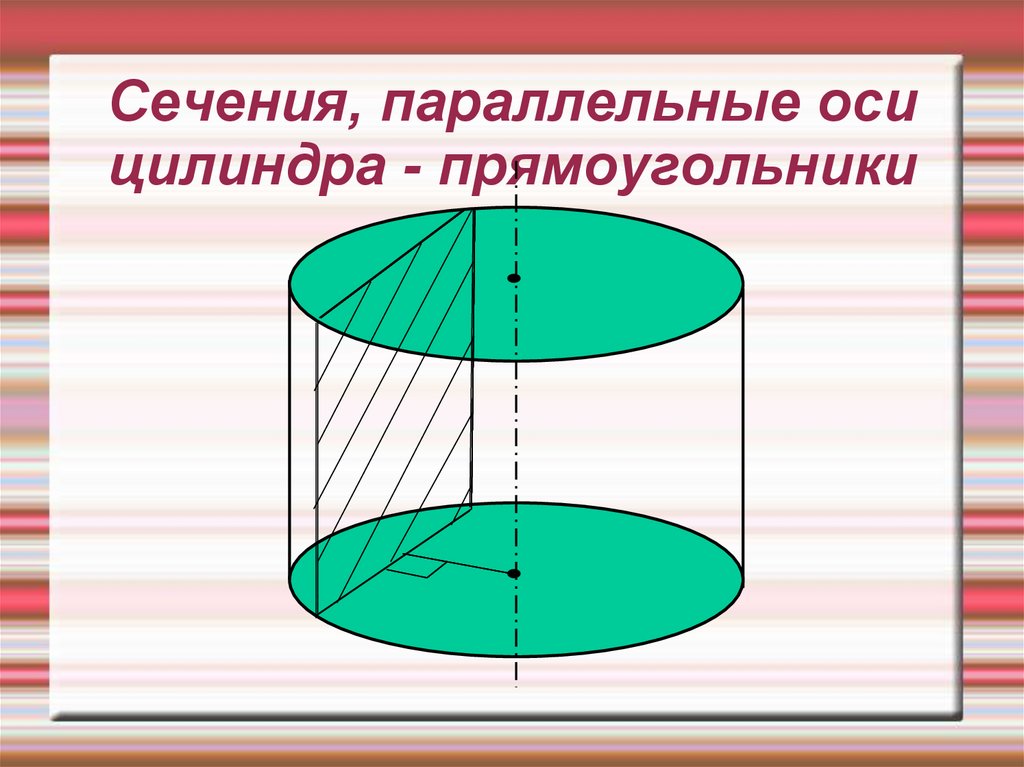
3.Сечения цилиндра
Сечение , параллельное оси
цилиндра-прямоугольник
о1
α
γ
β
β
о
Сечение плоскостью,
перпендикулярной к оси или
параллельное основаниям,
является кругом.

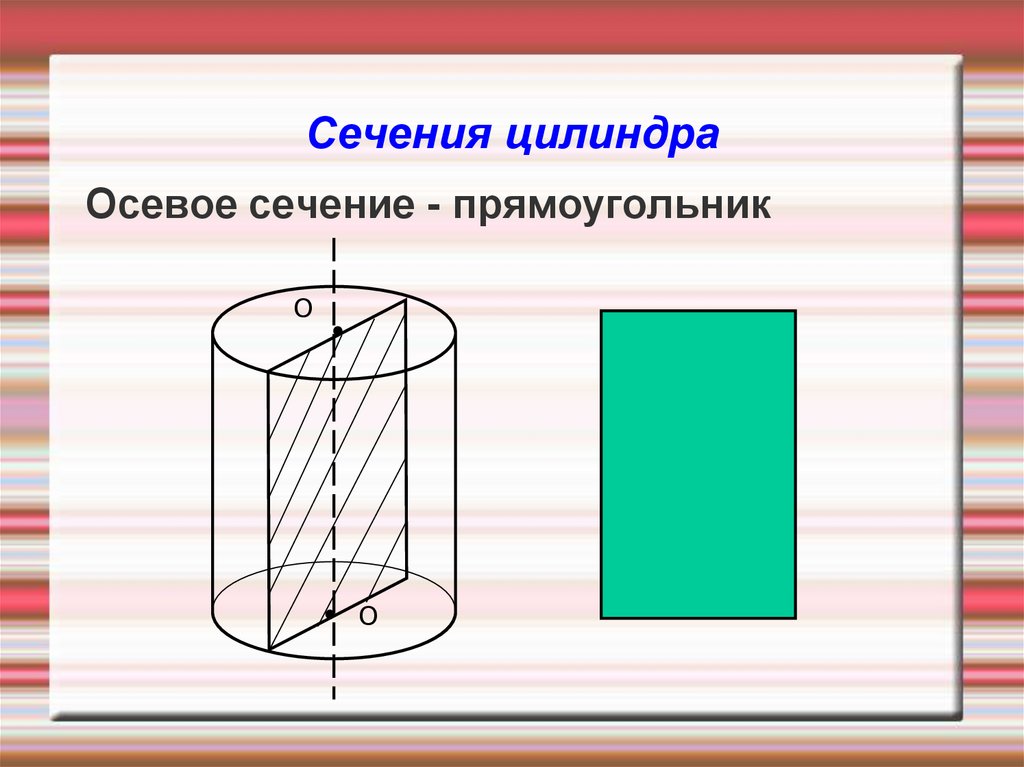
14. Сечения цилиндра

Осевое сечение - прямоугольник
О
О

15. Сечения, параллельные оси цилиндра - прямоугольники

16.

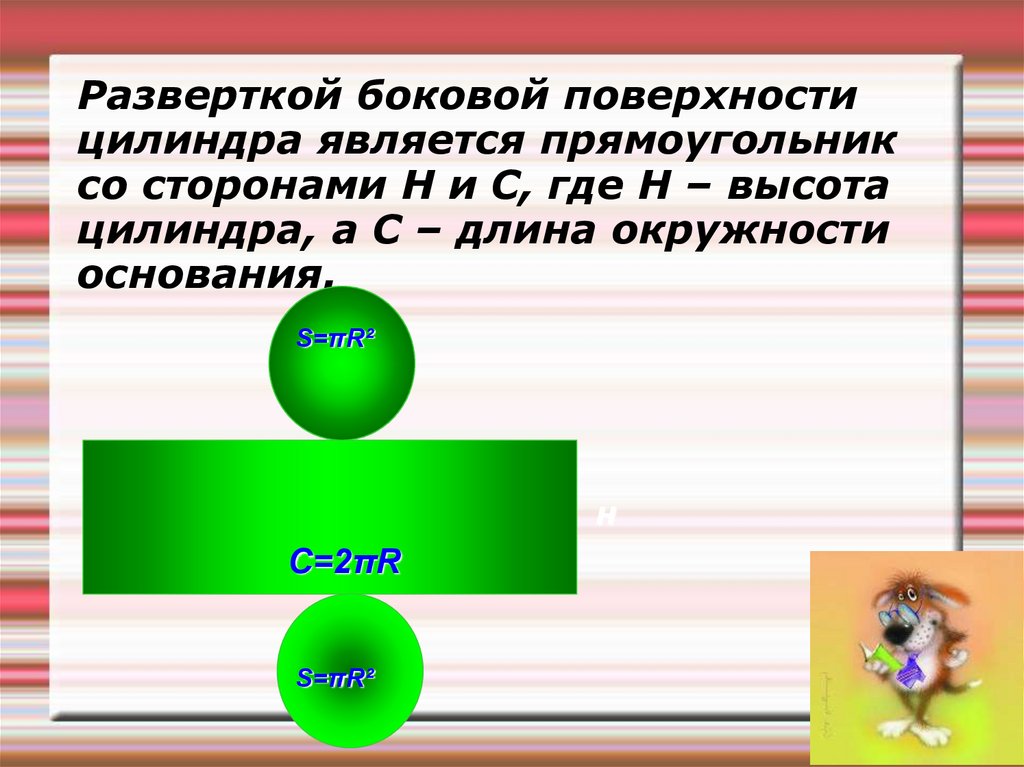
Разверткой боковой поверхности
цилиндра является прямоугольник
со сторонами Н и С, где Н – высота
цилиндра, а С – длина окружности
основания.
S=πR²
н
С=2πR
S=πR²

17.

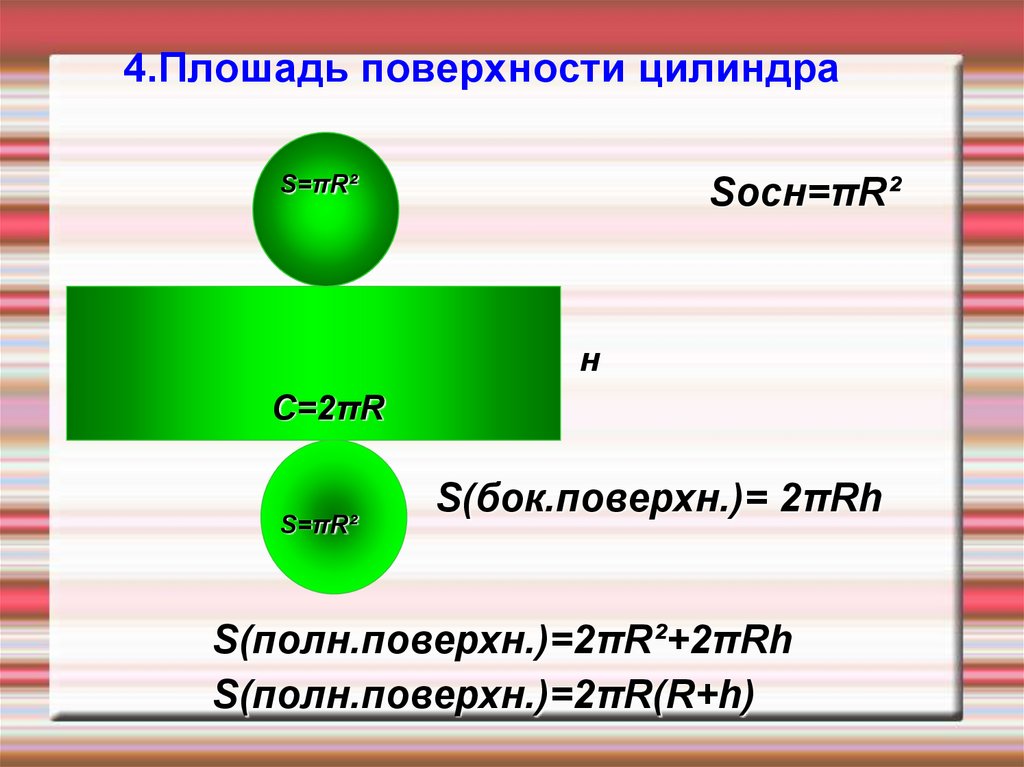
4.Плошадь поверхности цилиндра
S=πR²
Sосн=πR²
н
С=2πR
S=πR²
S(бок.поверхн.)= 2πRh
S(полн.поверхн.)=2πR²+2πRh
S(полн.поверхн.)=2πR(R+h)

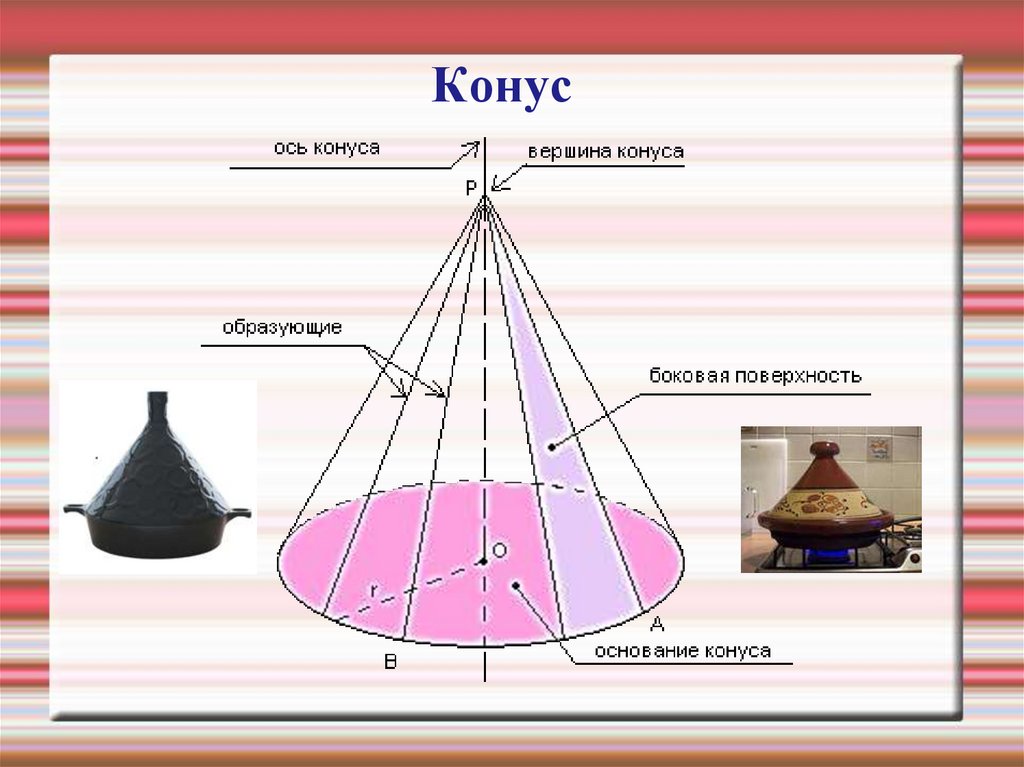
18. Конус -

Конус это тело, ограниченное
конической поверхностью и
кругом с границей L

19. Конус

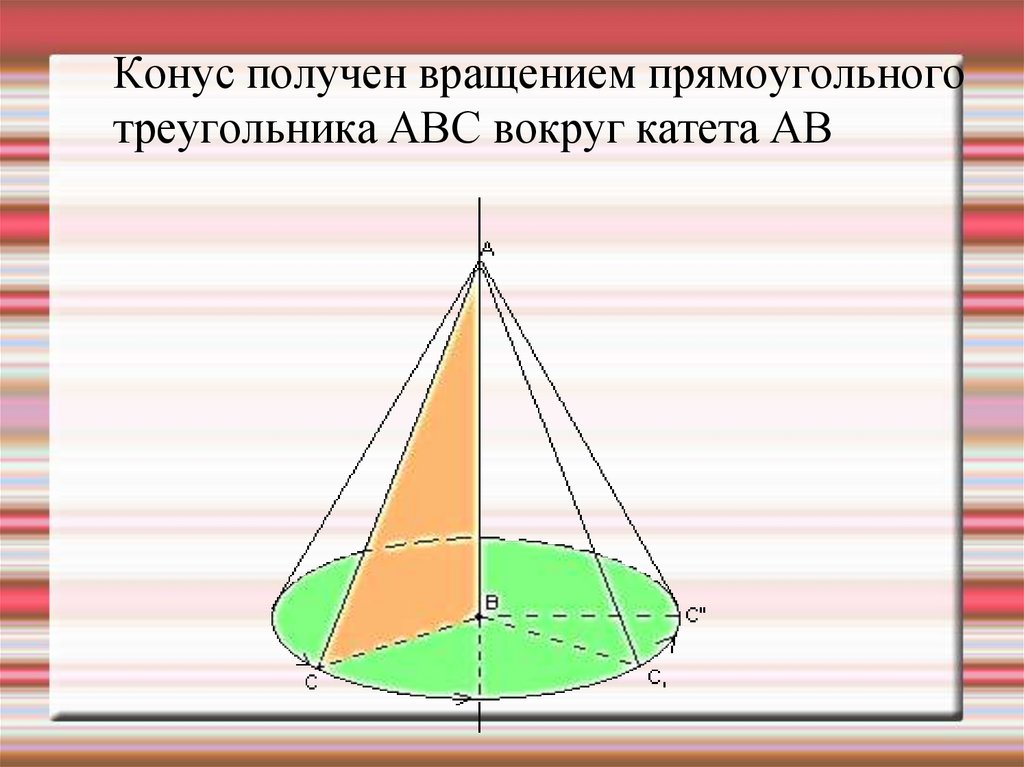
20. Конус получен вращением прямоугольного треугольника АВС вокруг катета АВ

21. Осевое сечение конуса

Если секущая плоскость
проходит через ось
конуса, то сечение
представляет собой
равнобедренный
треугольник, основание
которого- диаметр
основания конуса, а
боковые стороныобразующие конуса. Это
сечение- осевое.

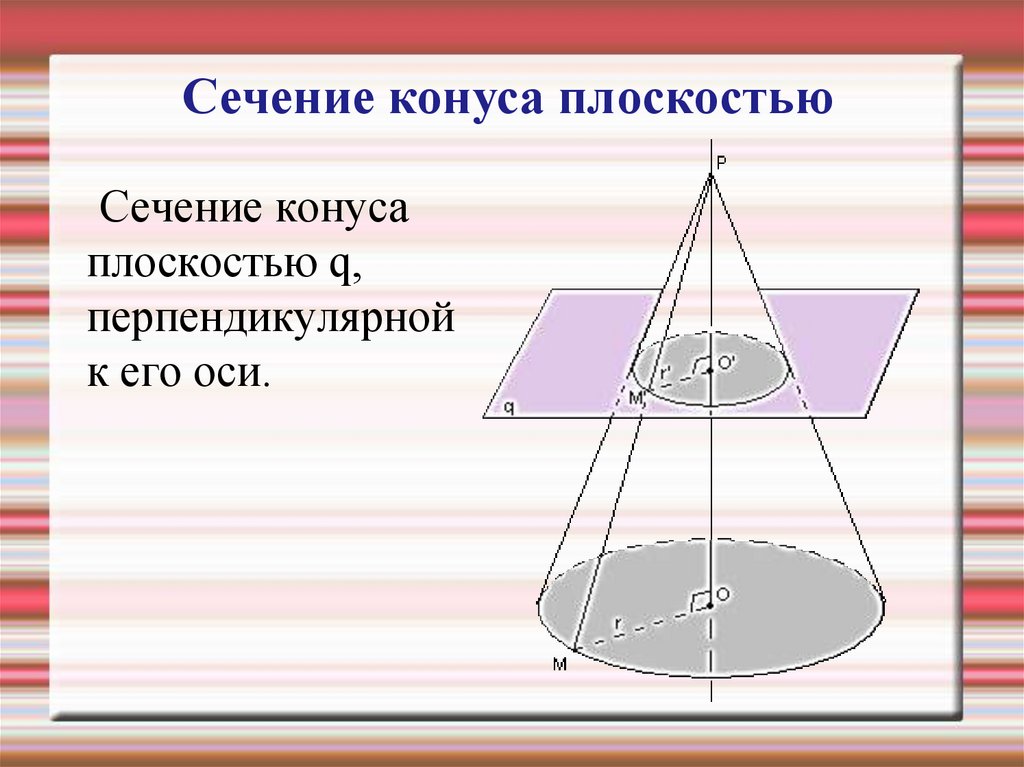
22.

Сечение конуса плоскостью
Сечение конуса
плоскостью q,
перпендикулярной
к его оси.

23. Площадь поверхности конуса

Площадь боковой
За площадь боковой
поверхности конуса
поверхности конуса
равна произведению
принимается
половины длины
площадь её
окружности
развертки.
основания на
образующую. S=πrl
Площадь полной
поверхности конусасумма площадей
боковой поверхности
и основания.S=πr(l+r)

24.

Конус можно рассмотреть в различных
предметах, начиная с обычного
мороженого и заканчивая техникой .

25. Нахождение конуса в природе

В природе мы часто встречаем конус. Например, в песчаной
пустыне Сахаре, где сами холмы представляют собой конус.

26.

«Конусами» называется семейство морских моллюсков.
Конусов свыше 500 видов. Живут в тропиках и
субтропиках, являются хищниками, имеют ядовитую
железу. Укус конусов очень болезнен. Известны
смертельные случаи. Раковины используются как
украшения, сувениры.

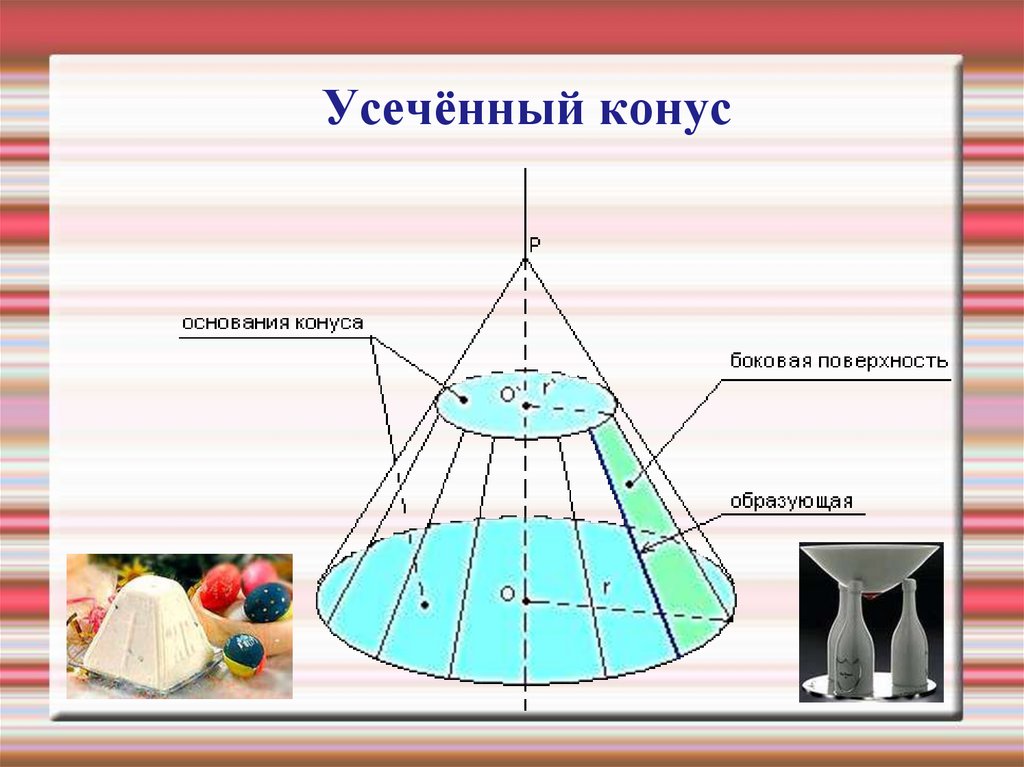
27. Усечённый конус

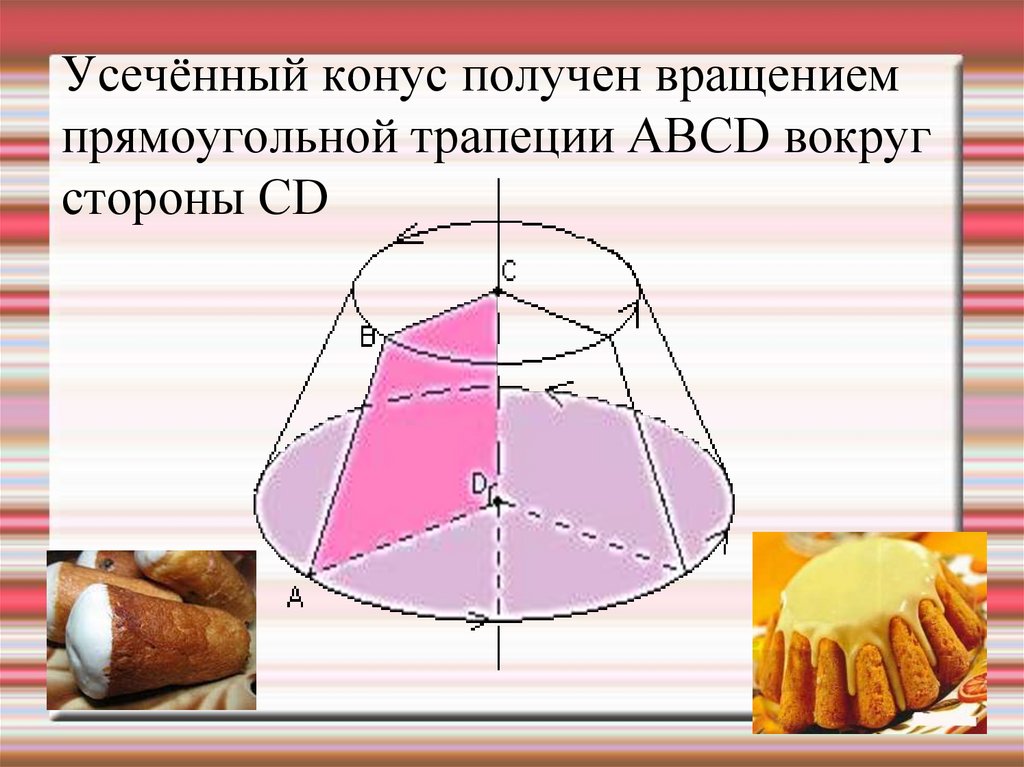
28. Усечённый конус получен вращением прямоугольной трапеции АВСD вокруг стороны CD

29. Площадь боковой поверхности усечённого конуса

равна произведению полусуммы длин
окружностей оснований на образующую:
S = π (r + r₁) l

30. Задача №1:Найти площадь полной поверхности цилиндра

Решение задач
Задача №1:Найти площадь полной
поверхности цилиндра
В
5
А
45º
r
С
АВС
- прямоугольный
АВС
- равнобедренный
ВС=АС=5
r=2,5
S=2πr(h+r)
S=2π·2,5(5 + 2,5)= 5π·7,5 = 37,5π

31.

Задача №2:Площадь осевого сечения
цилиндра равна 10 м2, а площадь основания
равна 5 м2. Найдите высоту цилиндра.
R 5,
2 R H 10
2
В
O1
С
H
А
R
O
5
R=
H
D
H=
5
2
5
5
H
м

32. Решение задач на нахождение площадей боковой и полной поверхности конуса, усечённого конуса

Решение задач
Решение задач на нахождение площадей боковой
и полной поверхности конуса, усечённого конуса
l
r

33. Решение задач на нахождение площадей боковой и полной поверхности конуса, усечённого конуса.

Задача 2. Сколько потребуется посыпки на торт
«Муравейник» диаметром основания 26 см, и высотой 15
см, если на каждый квадратный сантиметр ее требуется 3 г.
Рекомендации к решению: Торт «Муравейник» имеет форму
конуса, вся посыпка представляет собой боковую
поверхность. Зная диаметр найдем радиус, зная высоту и
радиус найдем образующую, а затем и площадь боковой
поверхности, т.е. площадь поверхности посыпки.

34.

Спасибо за внимание!