Similar presentations:
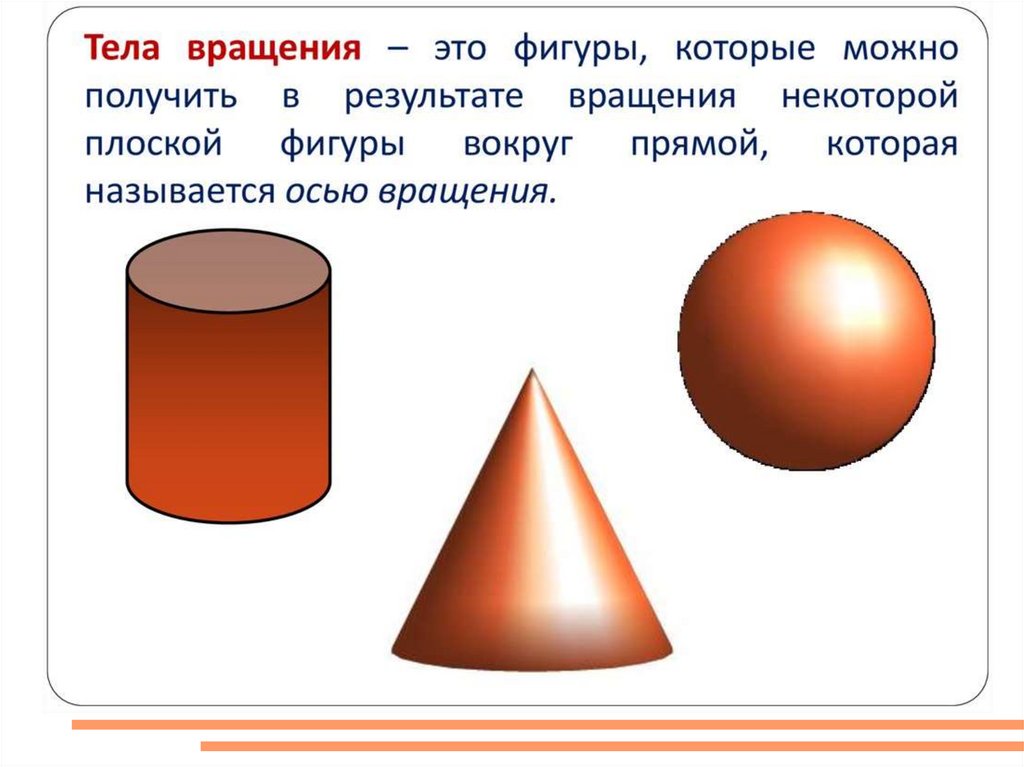
Тела вращения. Цилиндр. Конус
1.
Занятие 66. Тела вращения.Цилиндр. Конус.
2.
3.
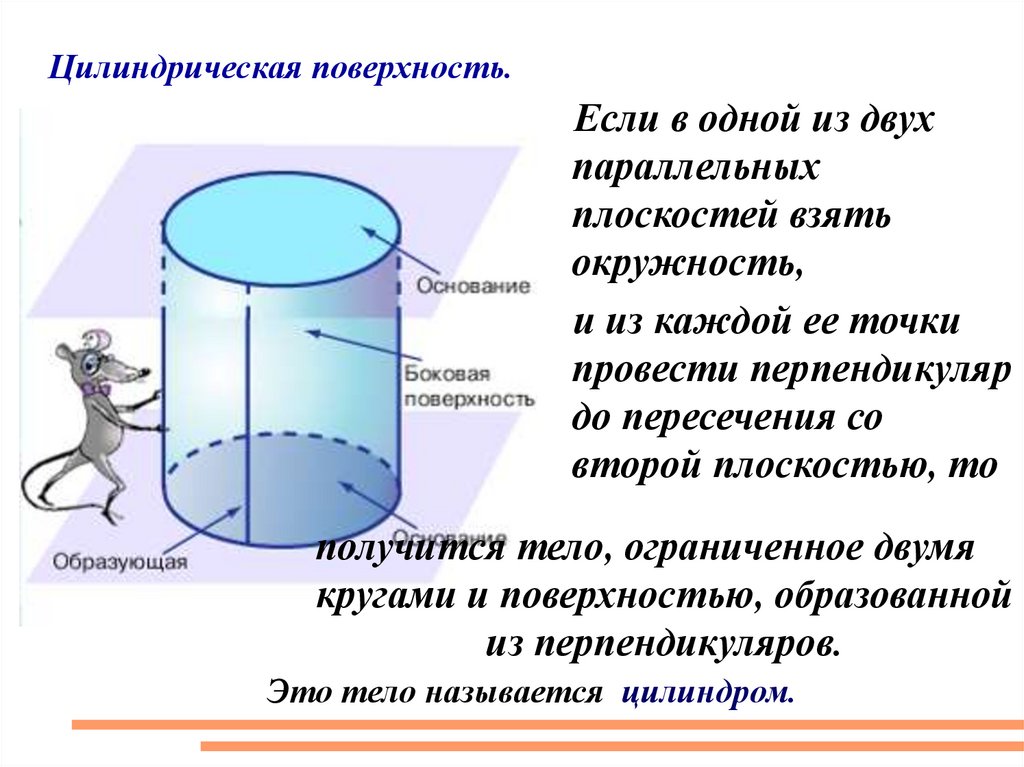
Цилиндрическая поверхность.Если в одной из двух
параллельных
плоскостей взять
окружность,
и из каждой ее точки
провести перпендикуляр
до пересечения со
второй плоскостью, то
получится тело, ограниченное двумя
кругами и поверхностью, образованной
из перпендикуляров.
Это тело называется цилиндром.
4.
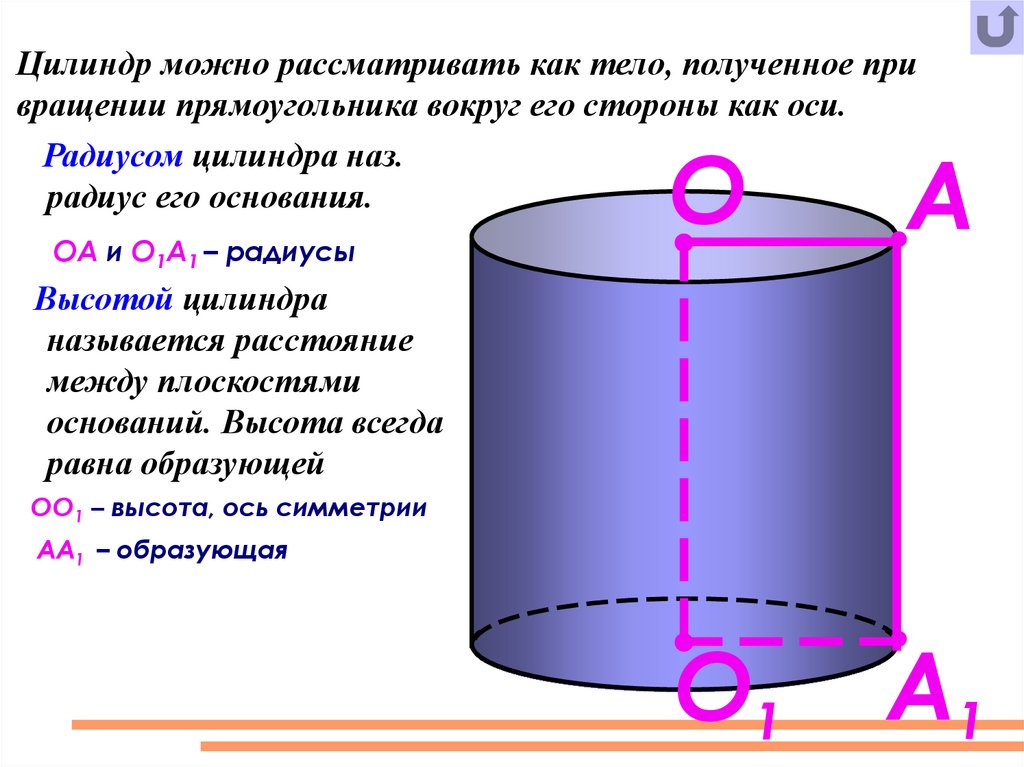
Цилиндр можно рассматривать как тело, полученное привращении прямоугольника вокруг его стороны как оси.
Радиусом цилиндра наз.
радиус его основания.
ОА и О1А1 – радиусы
О
А
О1
А1
Высотой цилиндра
называется расстояние
между плоскостями
оснований. Высота всегда
равна образующей
ОО1 – высота, ось симметрии
АА1 – образующая
5.
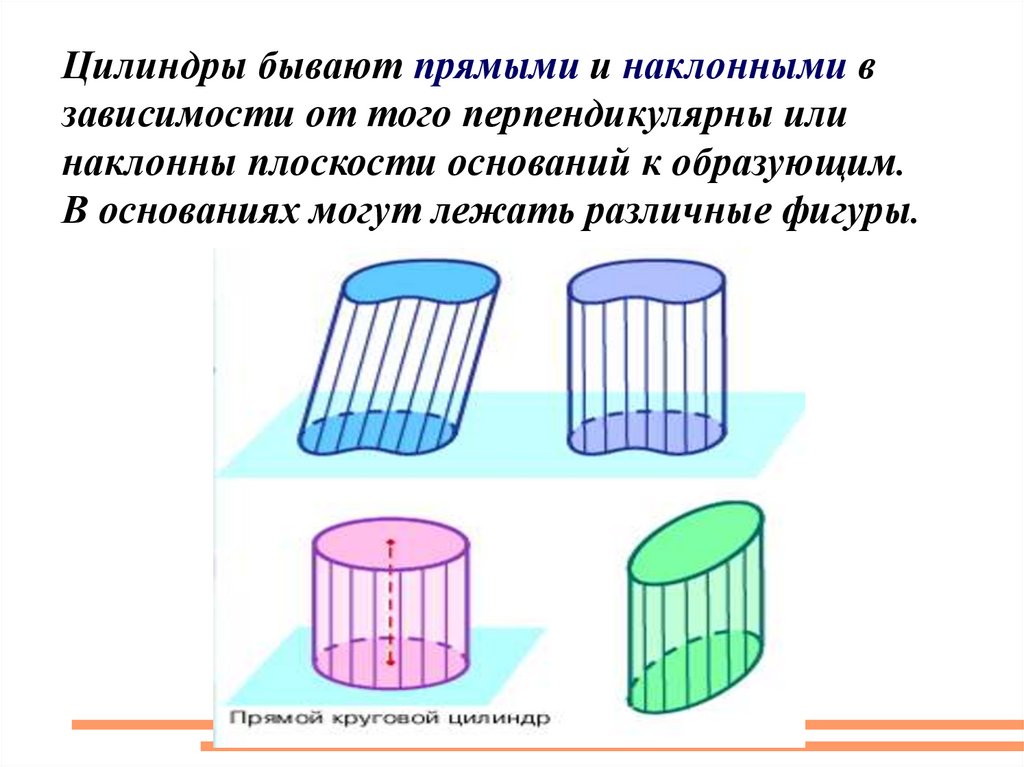
Цилиндры бывают прямыми и наклонными взависимости от того перпендикулярны или
наклонны плоскости оснований к образующим.
В основаниях могут лежать различные фигуры.
6.
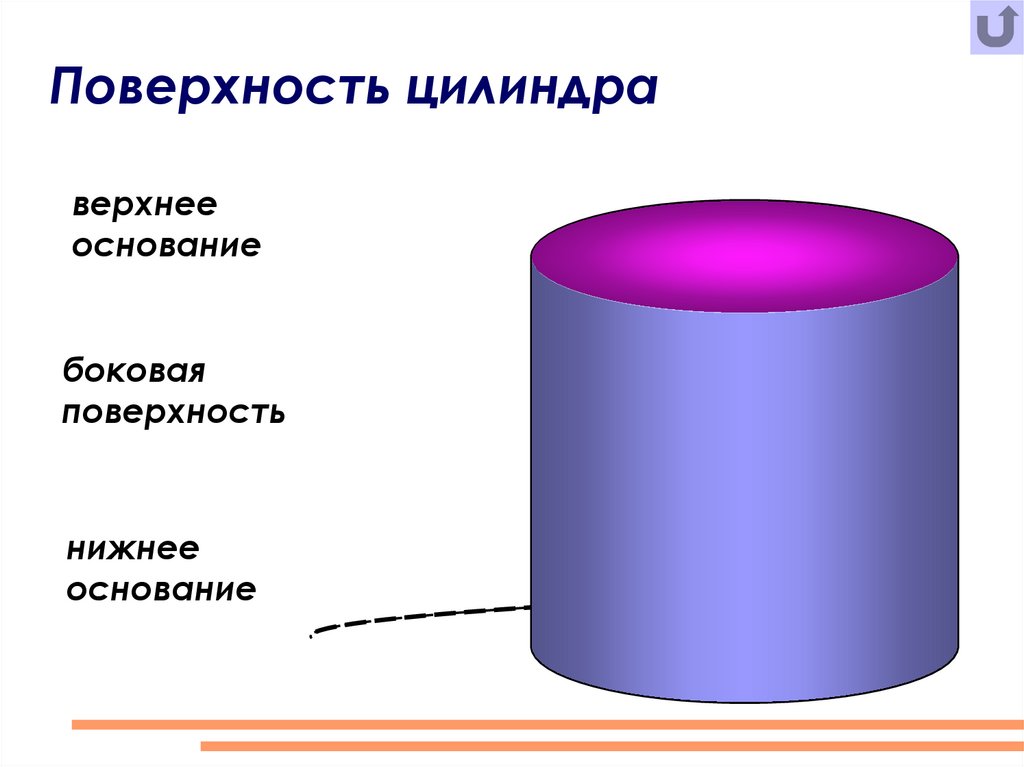
Поверхность цилиндраверхнее
основание
боковая
поверхность
нижнее
основание
7.
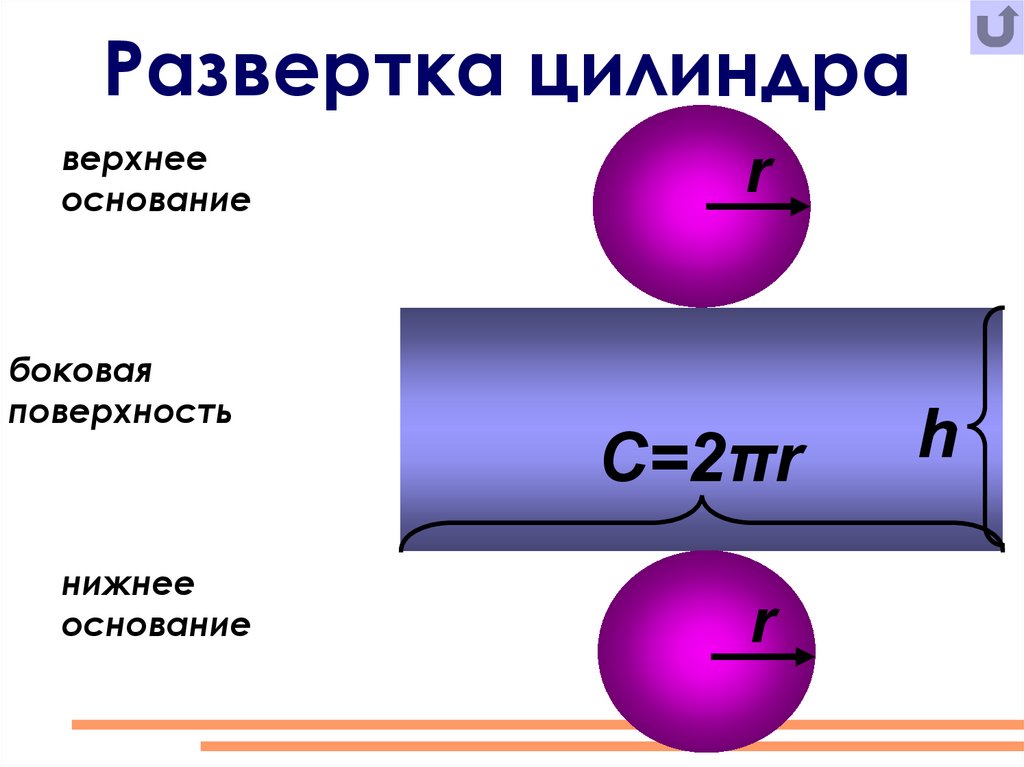
Развертка цилиндраверхнее
основание
r
боковая
поверхность
C=2πr
нижнее
основание
r
h
8.
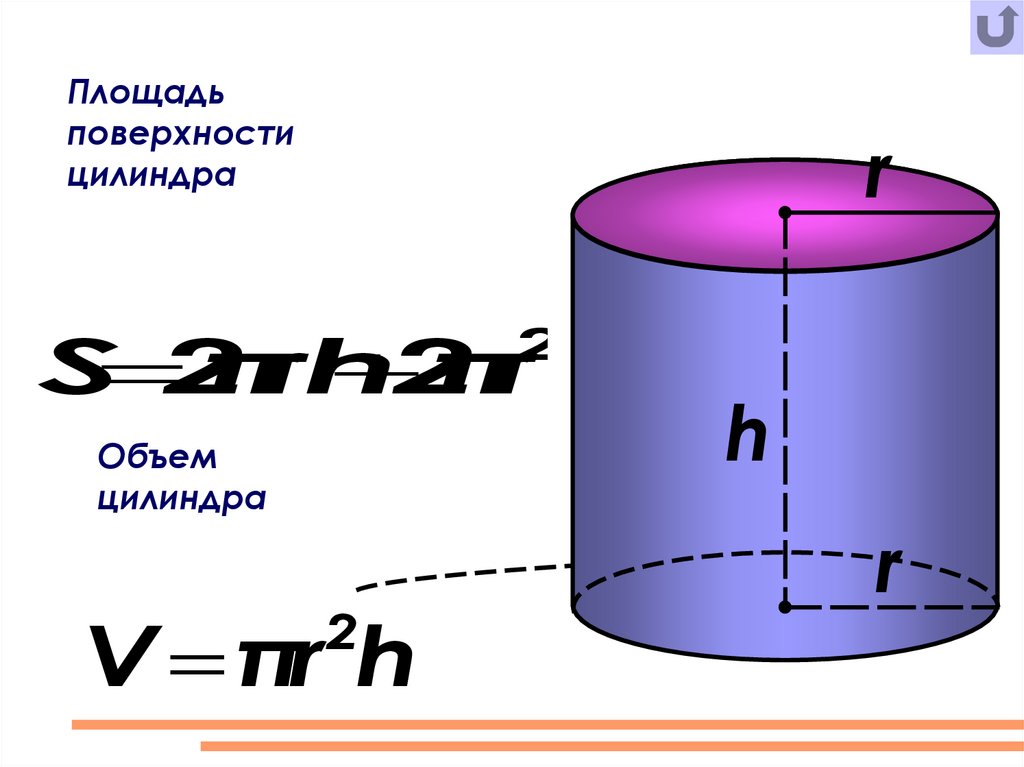
Площадьповерхности
цилиндра
r
2
S 2
π
rh
2
π
r
Объем
цилиндра
2
V πr h
h
r
9.
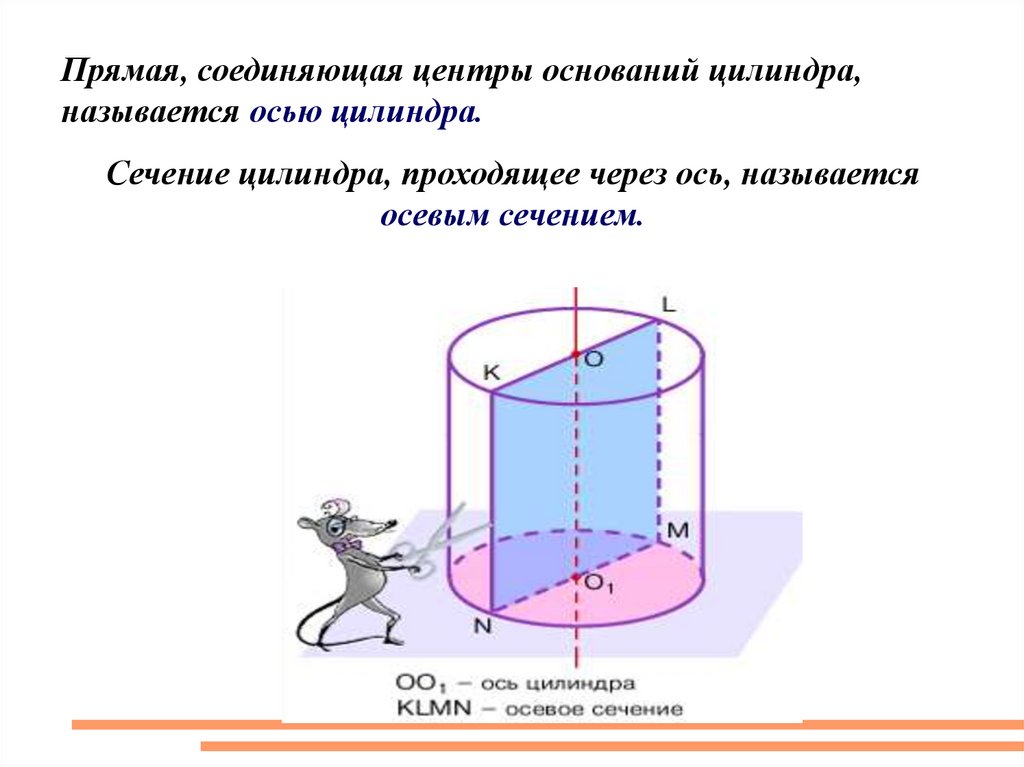
Прямая, соединяющая центры оснований цилиндра,называется осью цилиндра.
Сечение цилиндра, проходящее через ось, называется
осевым сечением.
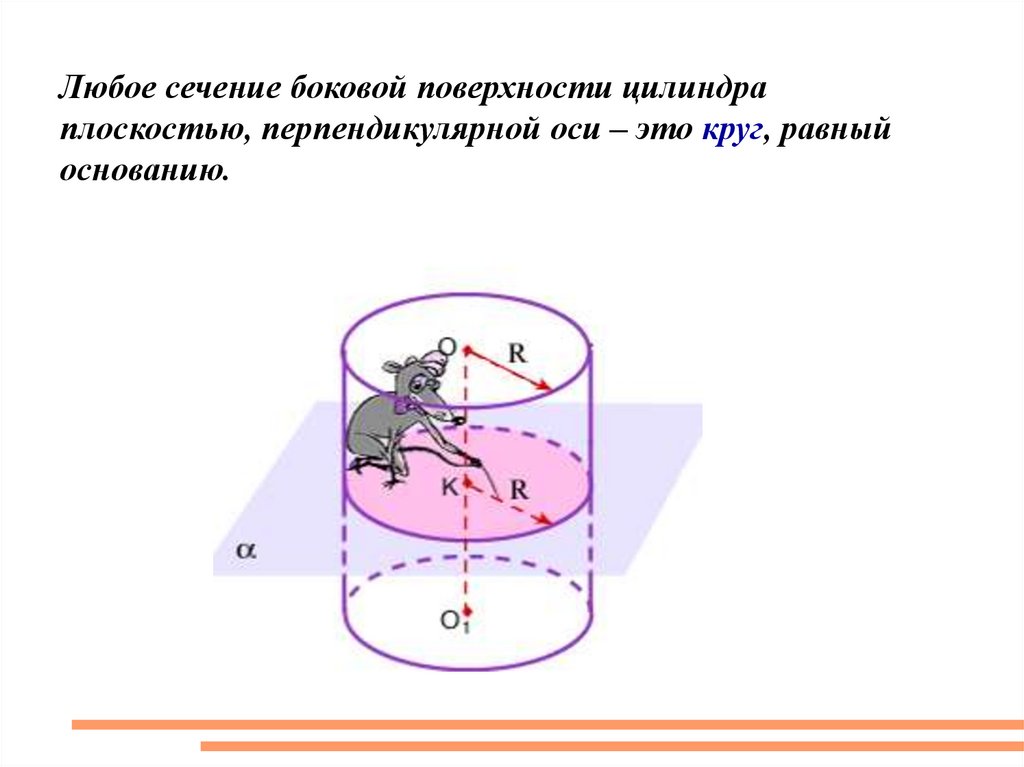
10.
Любое сечение боковой поверхности цилиндраплоскостью, перпендикулярной оси – это круг, равный
основанию.
11.
Конус – это фигура, полученнаявращением прямоугольного
треугольника АВС вокруг катета АВ
12.
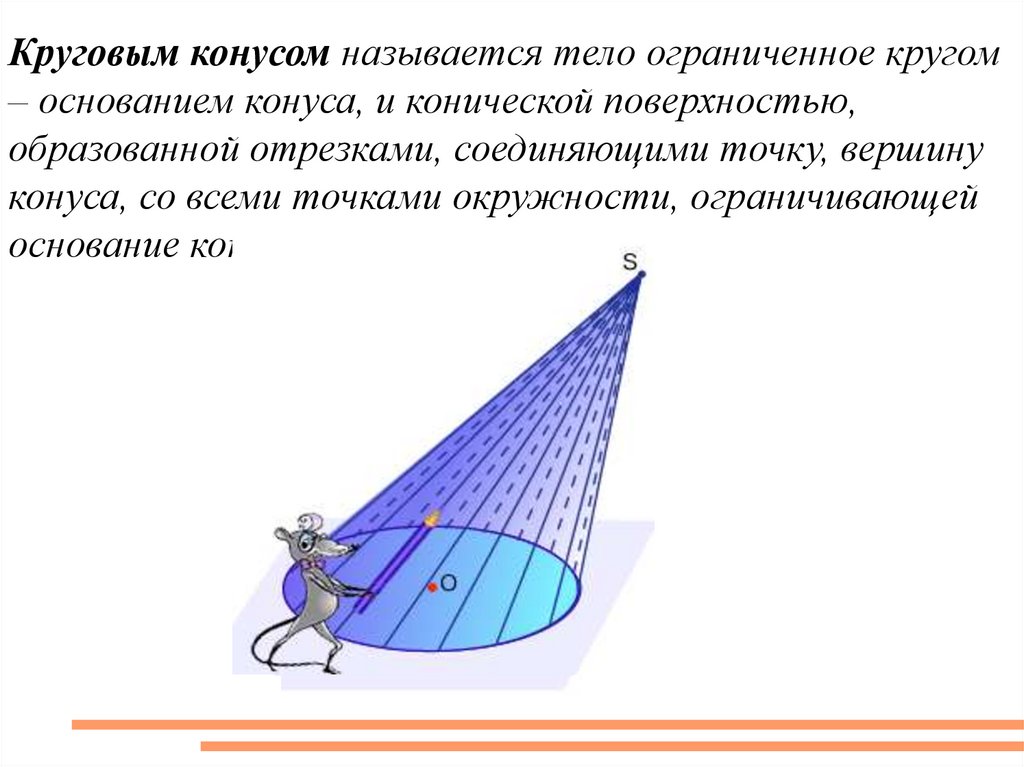
Круговым конусом называется тело ограниченное кругом– основанием конуса, и конической поверхностью,
образованной отрезками, соединяющими точку, вершину
конуса, со всеми точками окружности, ограничивающей
основание конуса.
13.
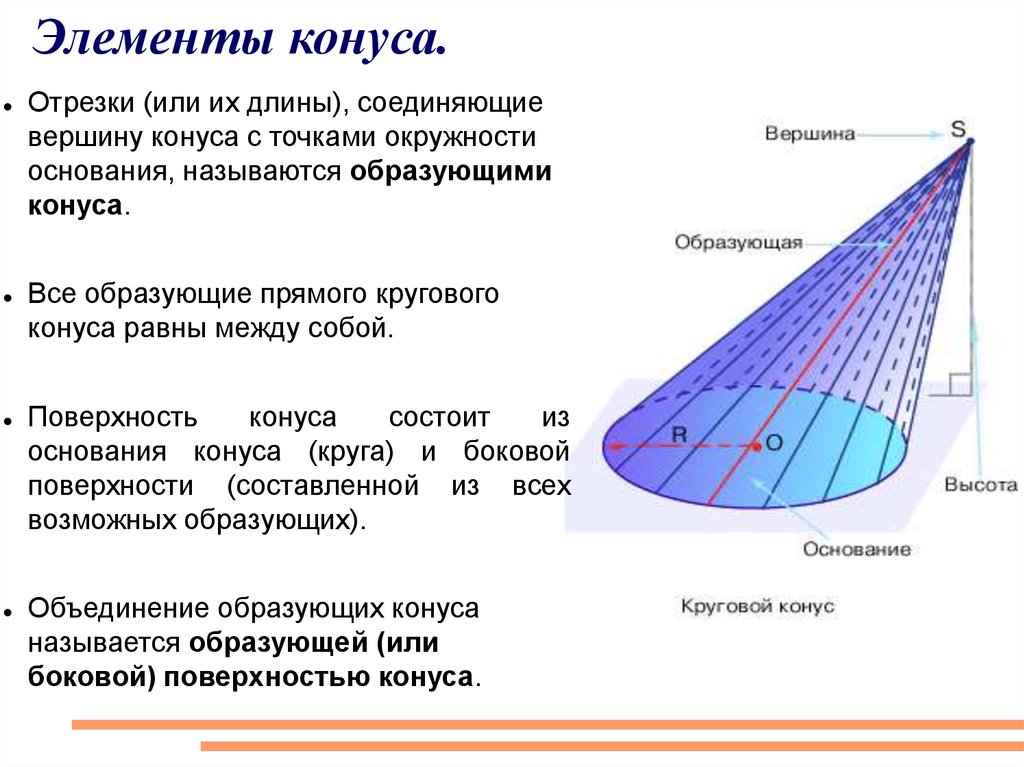
Элементы конуса.Отрезки (или их длины), соединяющие
вершину конуса с точками окружности
основания, называются образующими
конуса.
Все образующие прямого кругового
конуса равны между собой.
Поверхность
конуса
состоит
из
основания конуса (круга) и боковой
поверхности (составленной из всех
возможных образующих).
Объединение образующих конуса
называется образующей (или
боковой) поверхностью конуса.
14.
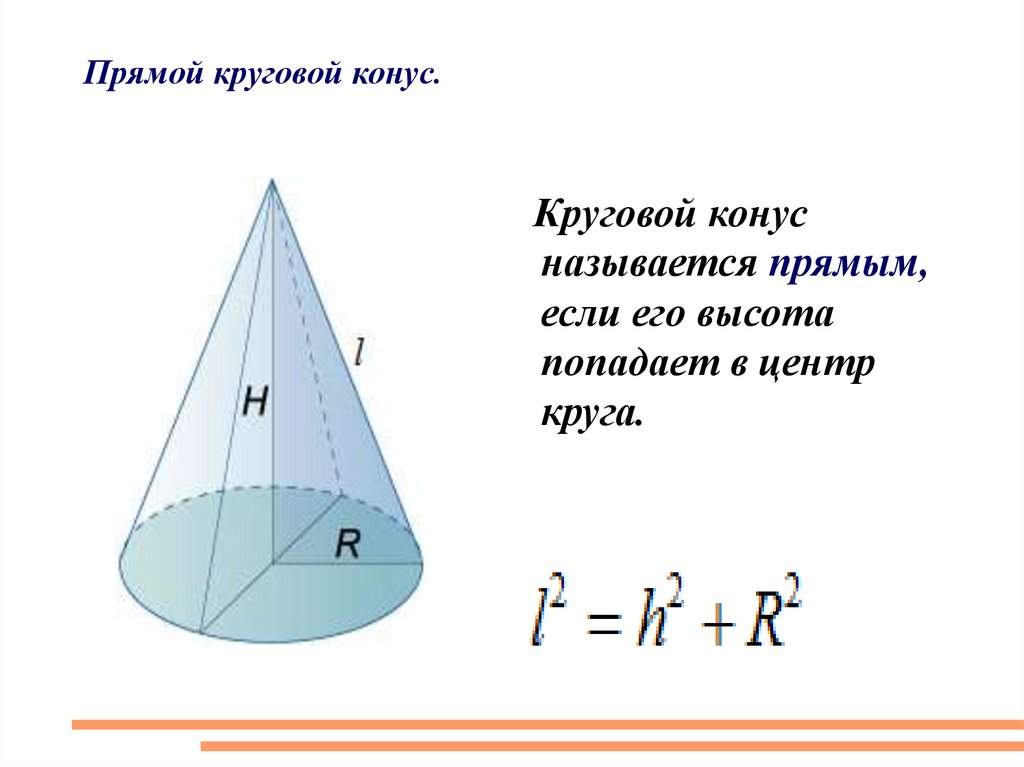
Прямой круговой конус.Круговой конус
называется прямым,
если его высота
попадает в центр
круга.
15.
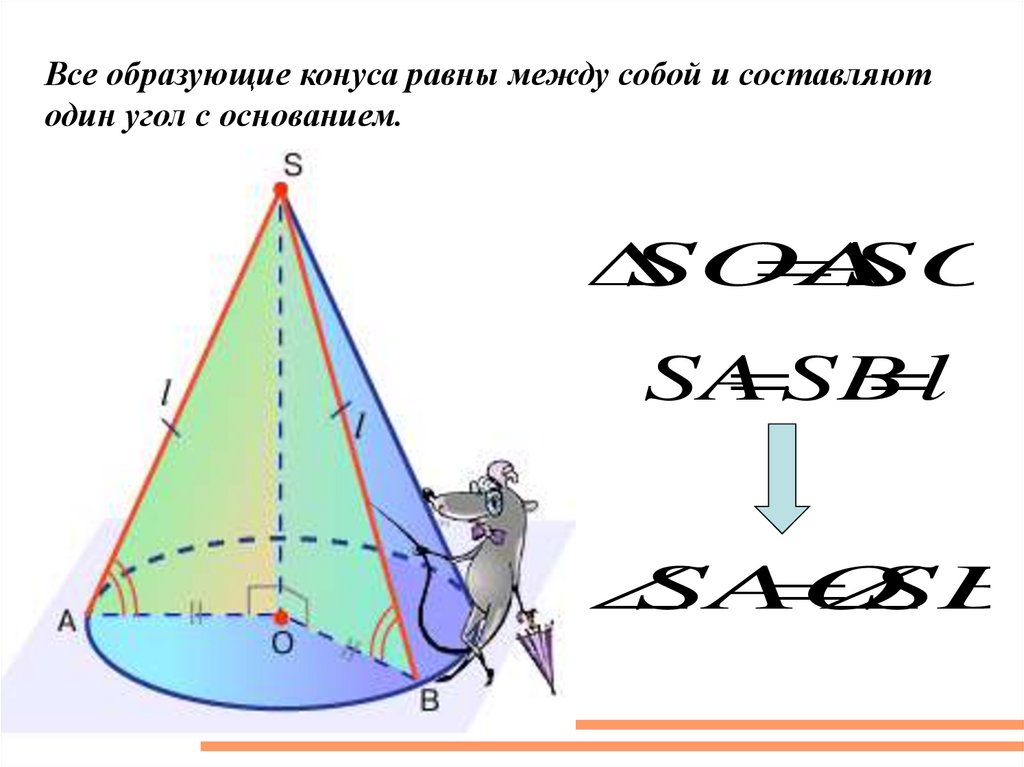
Все образующие конуса равны между собой и составляютодин угол с основанием.
SOA
SOB
SA
SB
l
SAO
SB
16.
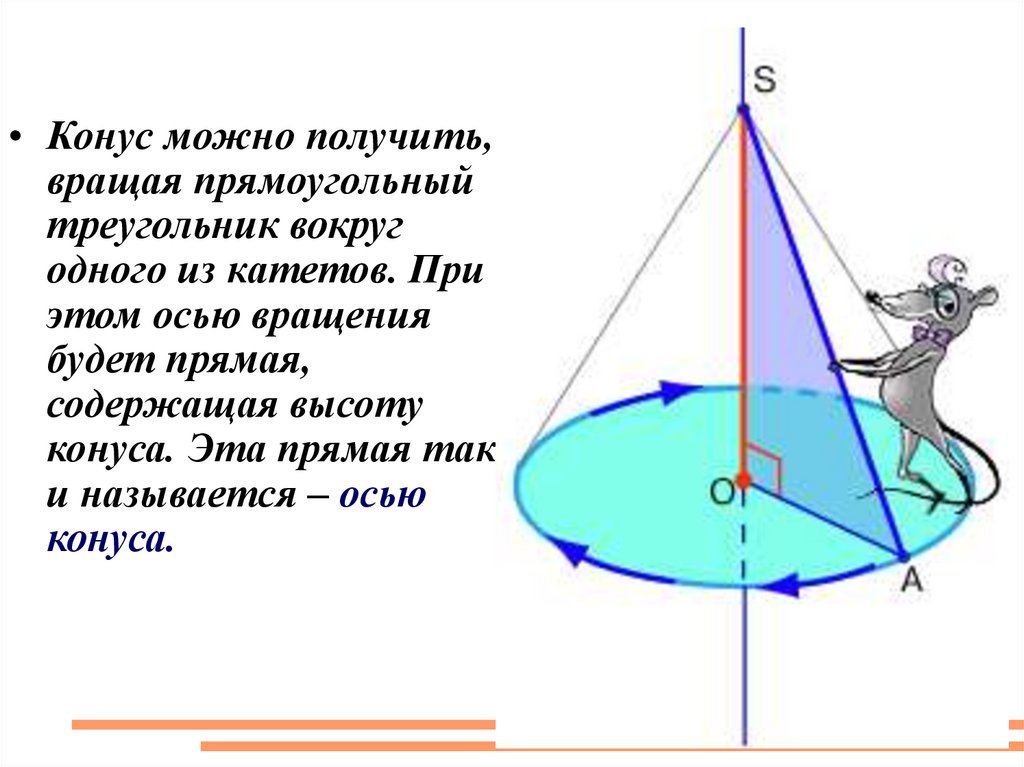
• Конус можно получить,вращая прямоугольный
треугольник вокруг
одного из катетов. При
этом осью вращения
будет прямая,
содержащая высоту
конуса. Эта прямая так
и называется – осью
конуса.
17.
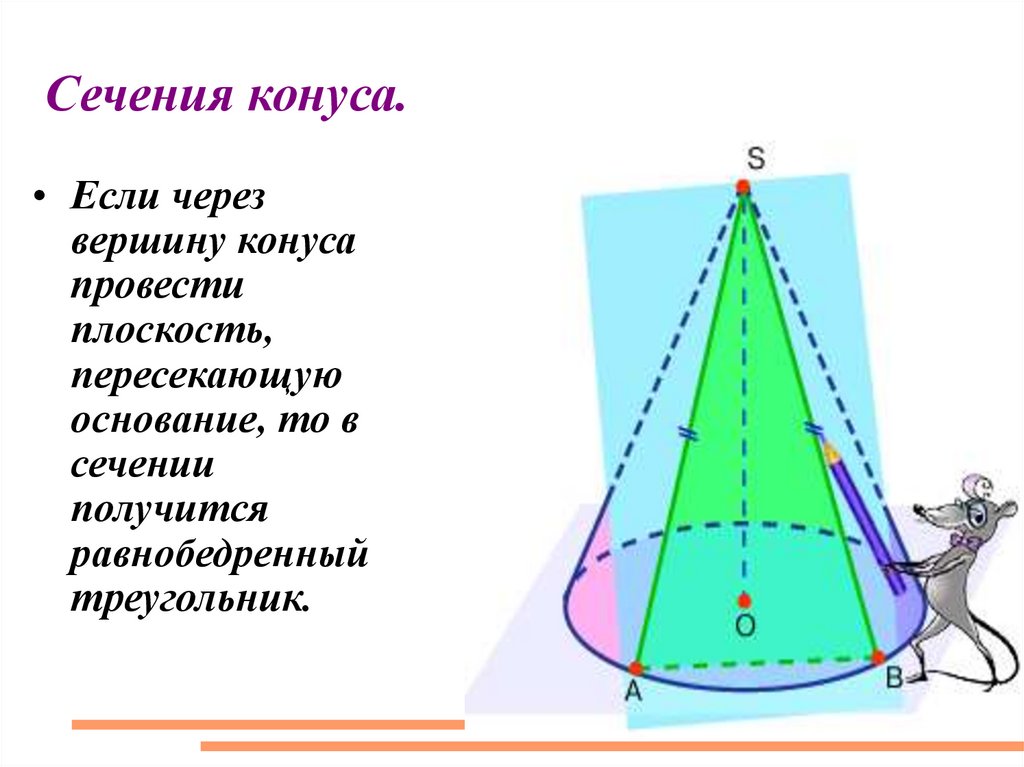
Сечения конуса.• Если через
вершину конуса
провести
плоскость,
пересекающую
основание, то в
сечении
получится
равнобедренный
треугольник.
18.
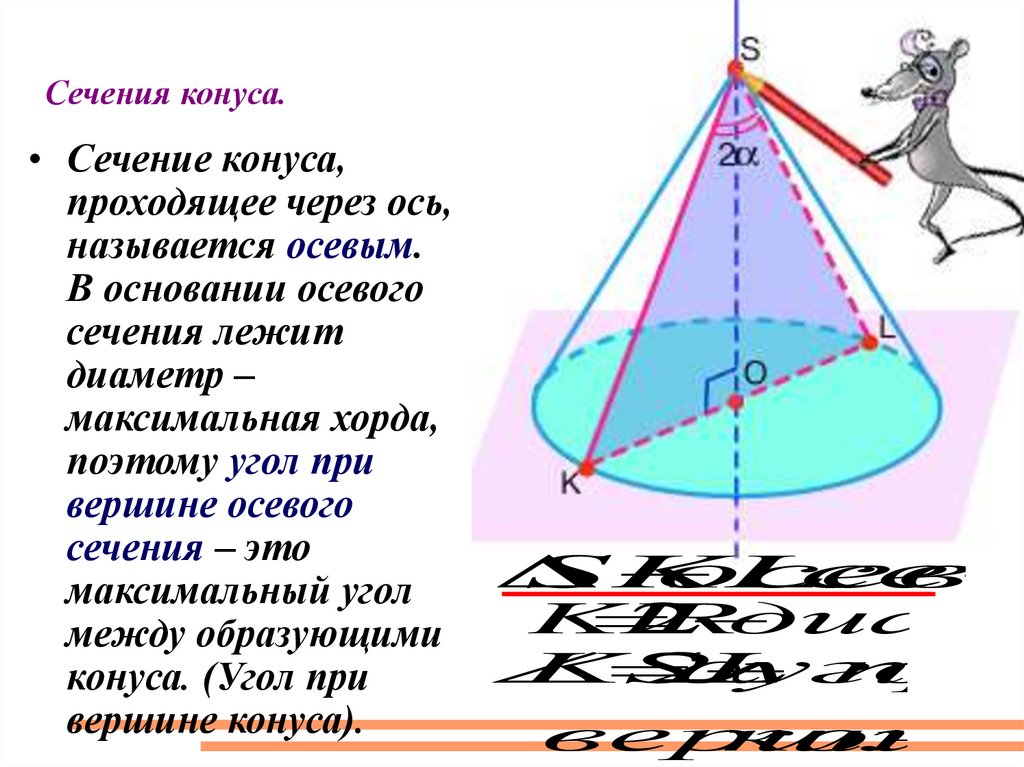
Сечения конуса.• Сечение конуса,
проходящее через ось,
называется осевым.
В основании осевого
сечения лежит
диаметр –
максимальная хорда,
поэтому угол при
вершине осевого
сечения – это
SKL
осево
сеч
максимальный угол
KL
2
Rдиам
между образующими
KSL
2
угол
при
конуса. (Угол при
вершине конуса).
вершине
конус
.
19.
Сечения конуса.• Любое сечение
конуса
плоскостью,
параллельной
основанию, - это
круг.
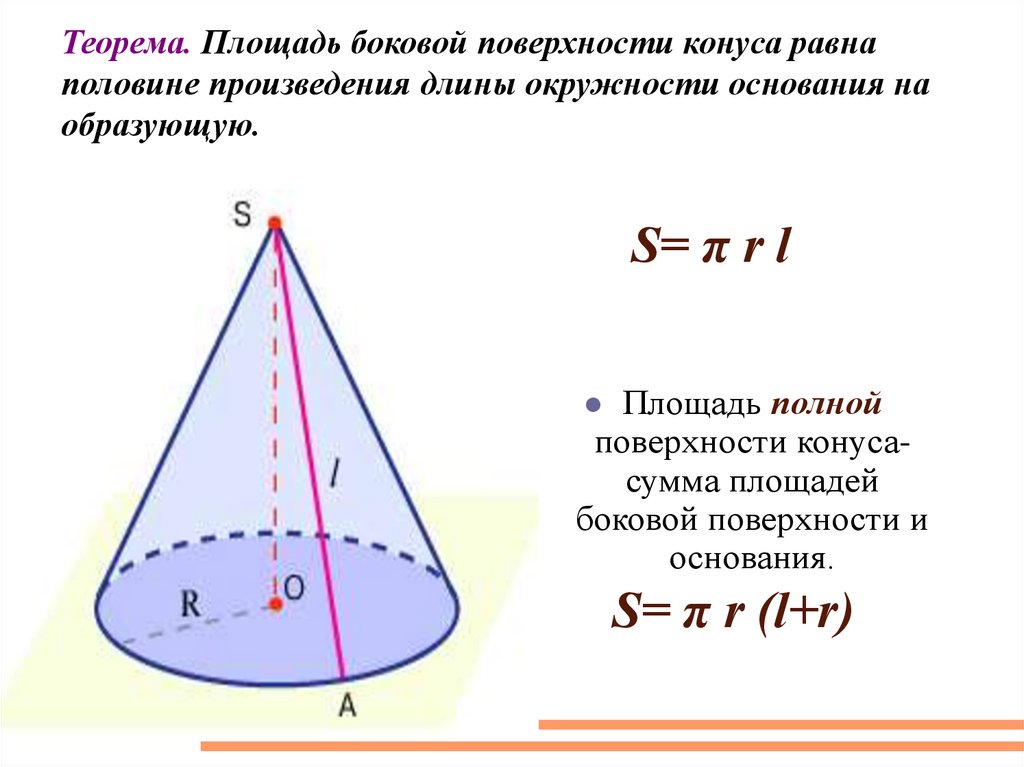
20.
Теорема. Площадь боковой поверхности конуса равнаполовине произведения длины окружности основания на
образующую.
S= π r l
Площадь полной
поверхности конусасумма площадей
боковой поверхности и
основания.
S= π r (l+r)
21.
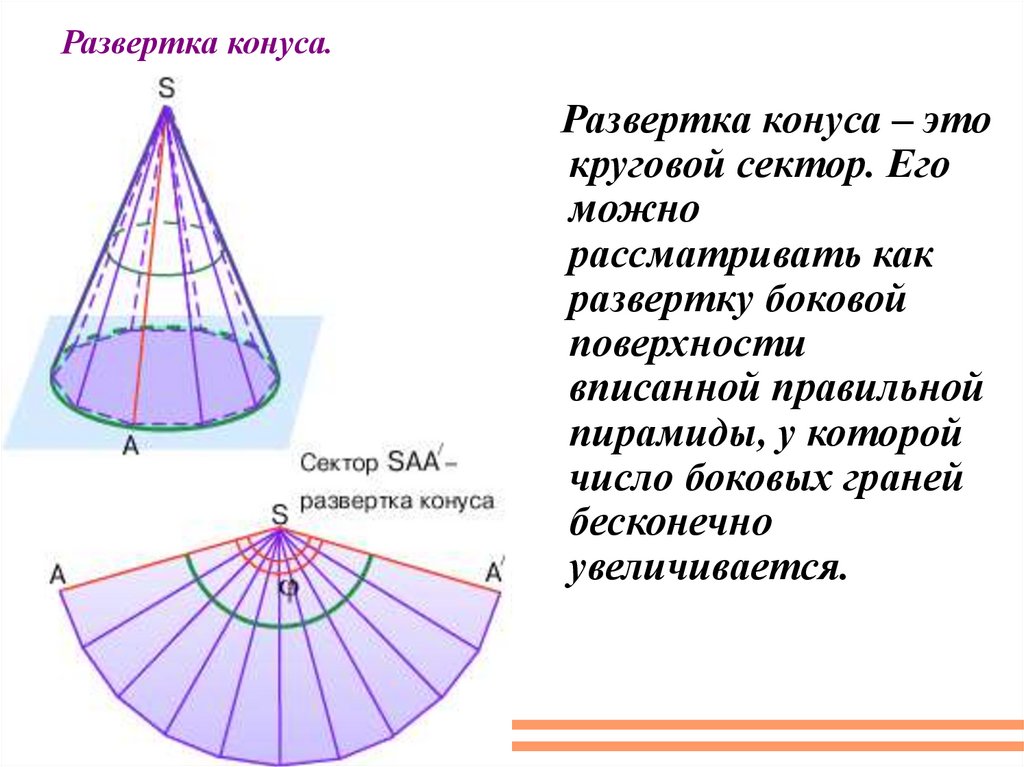
Развертка конуса.Развертка конуса – это
круговой сектор. Его
можно
рассматривать как
развертку боковой
поверхности
вписанной правильной
пирамиды, у которой
число боковых граней
бесконечно
увеличивается.
22.
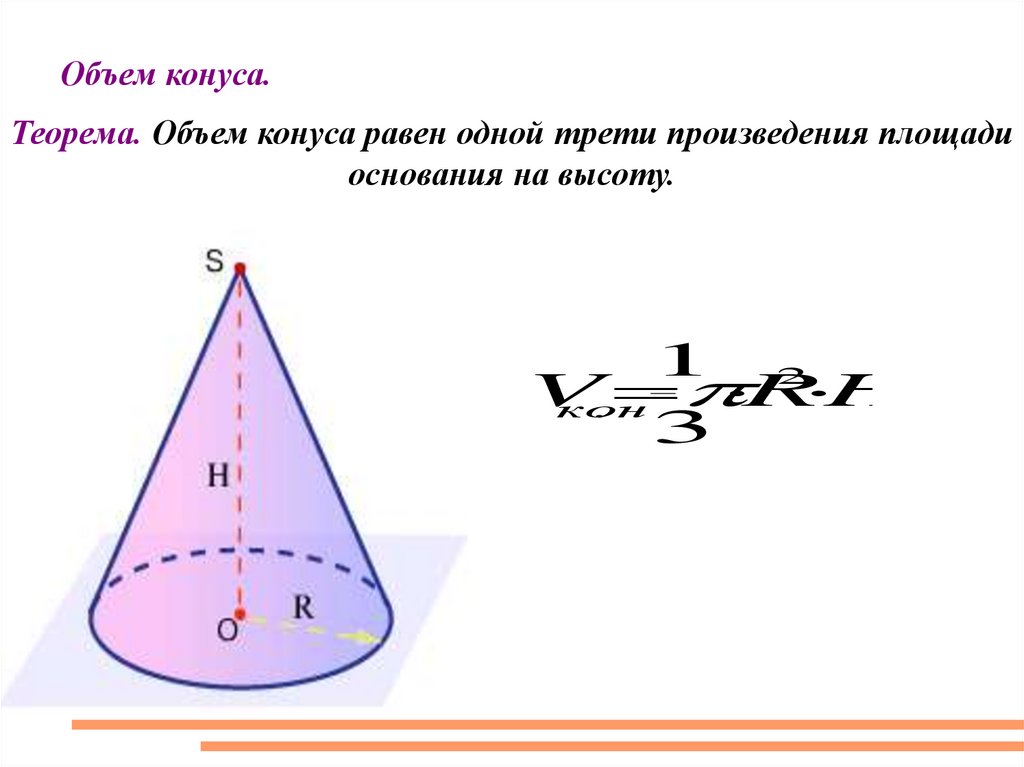
Объем конуса.Теорема. Объем конуса равен одной трети произведения площади
основания на высоту.
1 2
V
R H
кон
.
3



 mathematics
mathematics








