Цилиндр. Определение

1.

2. Определение.

• Цилиндр (греч. kýlindros, валик,
каток) — геометрическое тело,
ограниченное цилиндрической
поверхностью (называемой боковой
поверхностью цилиндра) и не более
чем двумя поверхностями
(основаниями цилиндра).

3. Другие определения цилиндра.

• Цилиндр - это фигура, состоящая из двух кругов,
совмещаемых параллельным переносом, и всех отрезков,
соединяющих соответствующие точки этих кругов.
• Цилиндром называется тело, ограниченное замкнутой
цилиндрической поверхностью и двумя параллельными
плоскостями, пересекающими эту поверхность.
• У Евклида цилиндр получается вращением прямоугольника.
• У Кавальери – движением образующей (при произвольной
направляющей – "цилиндрика").

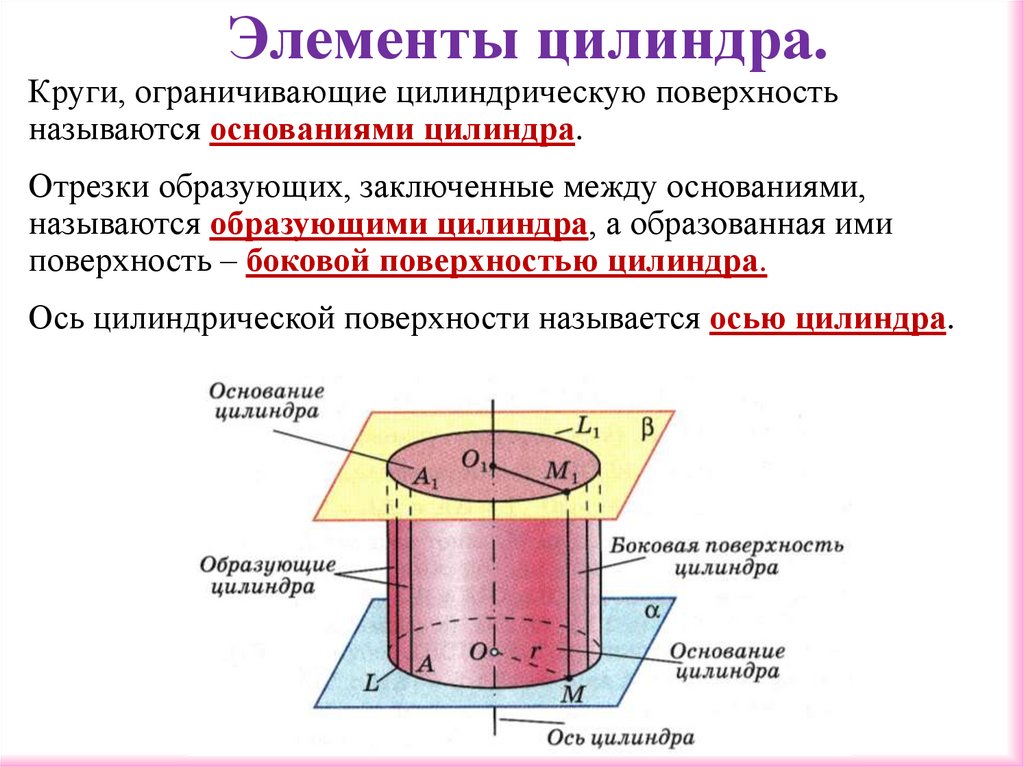
4. Элементы цилиндра.

Круги, ограничивающие цилиндрическую поверхность
называются основаниями цилиндра.
Отрезки образующих, заключенные между основаниями,
называются образующими цилиндра, а образованная ими
поверхность – боковой поверхностью цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.

5. Свойства цилиндра.

1. Основания равны и параллельны.
2. Образующие равны и параллельны.
3. Все сечения цилиндра плоскостями,
параллельными плоскостям оснований
цилиндра, равны основаниям цилиндра.

6. Доказательства свойств.

1. Основания циилиндра равны и параллельны.
Справедливость этого утверждения следует из того, что
множество концов образующих, лежащих в плоскости
β, получается из окружности L параллельным
переносом на вектор ОО1. Параллельный перенос
является движением и, значит, наложением, а при
наложении любая фигура переходит в равную ей
фигуру. Следовательно, при параллельном переносе на
вектор ОО1 окружность L перейдет в равную ей
окружность L1 радиуса r с центром в точке О1.
β
α
о1
о
L1
L

7.

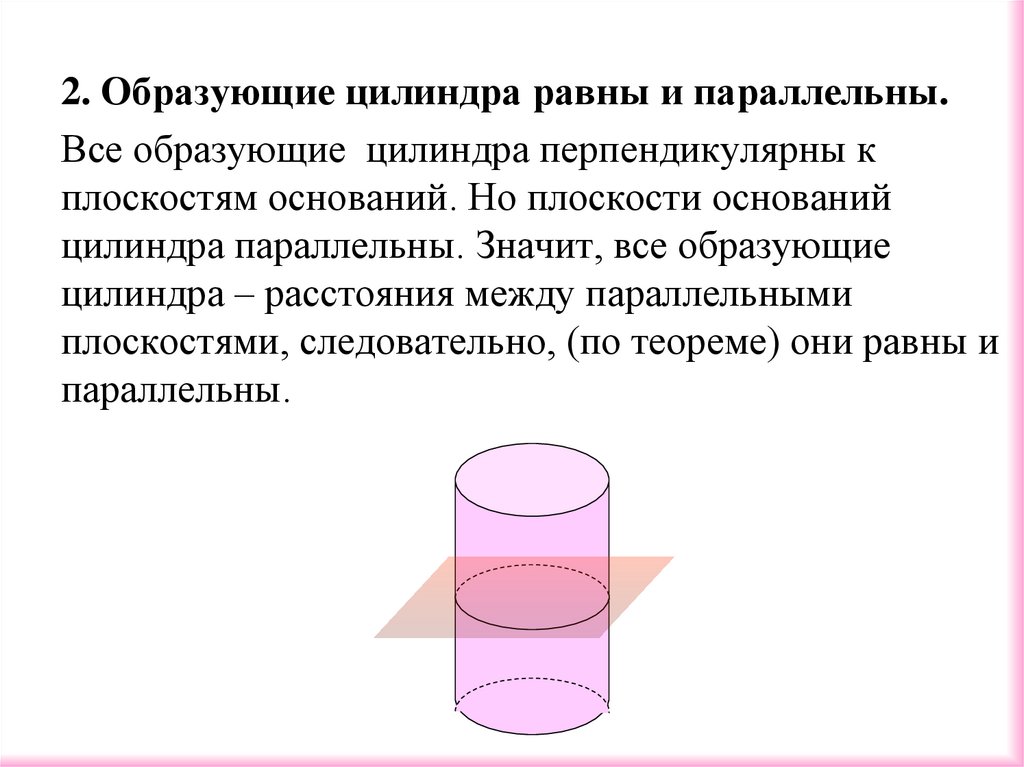
2. Образующие цилиндра равны и параллельны.
Все образующие цилиндра перпендикулярны к
плоскостям оснований. Но плоскости оснований
цилиндра параллельны. Значит, все образующие
цилиндра – расстояния между параллельными
плоскостями, следовательно, (по теореме) они равны и
параллельны.

8.

3. Все сечения цилиндра плоскостями,
параллельными плоскостям оснований цилиндра,
равны основаниям цилиндра.
Действительно, любое такое сечение является общим
основанием двух цилиндров, на которые секущая
плоскость разбивает данный цилиндр. Поэтому оно равно
другим основаниям этих цилиндров, которые являются
основаниями исходного цилиндра.

9. Влияние оснований на цилиндр.

• Если основания цилиндра плоские (и,
следовательно, содержащие их плоскости
параллельны), то цилиндр называют
стоящим на плоскости. Если основания
стоящего на плоскости цилиндра
перпендикулярны образующей, то цилиндр
называется прямым.
• В частности, если основание стоящего на
плоскости цилиндра — круг, то говорят о
круговом (круглом) цилиндре; если
эллипс — то эллиптическом.
β
α

10. Виды цилиндра.

• Бесконечное тело, ограниченное замкнутой бесконечной
цилиндрической поверхностью, называется бесконечным
цилиндром. Прямой круговой цилиндр — это поверхность,
образованная вращением одной из параллельных прямых
вокруг другой, принятой в качестве оси вращения.
• Бесконечное тело, ограниченное замкнутым
цилиндрическим лучом и его основанием, называется
открытым цилиндром. Основание и образующие
цилиндрического луча называют соответственно основанием
и образующими открытого цилиндра.
• Конечное тело, ограниченное замкнутой конечной
цилиндрической поверхностью и двумя выделившими её
сечениями, называется конечным цилиндром, или
собственно цилиндром. Сечения называются основаниями
цилиндра. По определению конечной цилиндрической
поверхности, основания цилиндра равны.

11.

Прямой цилиндр.

12.

Определение.
Прямым называется такой цилиндр, у
которого образующие перпендикулярны
основаниям.

13.

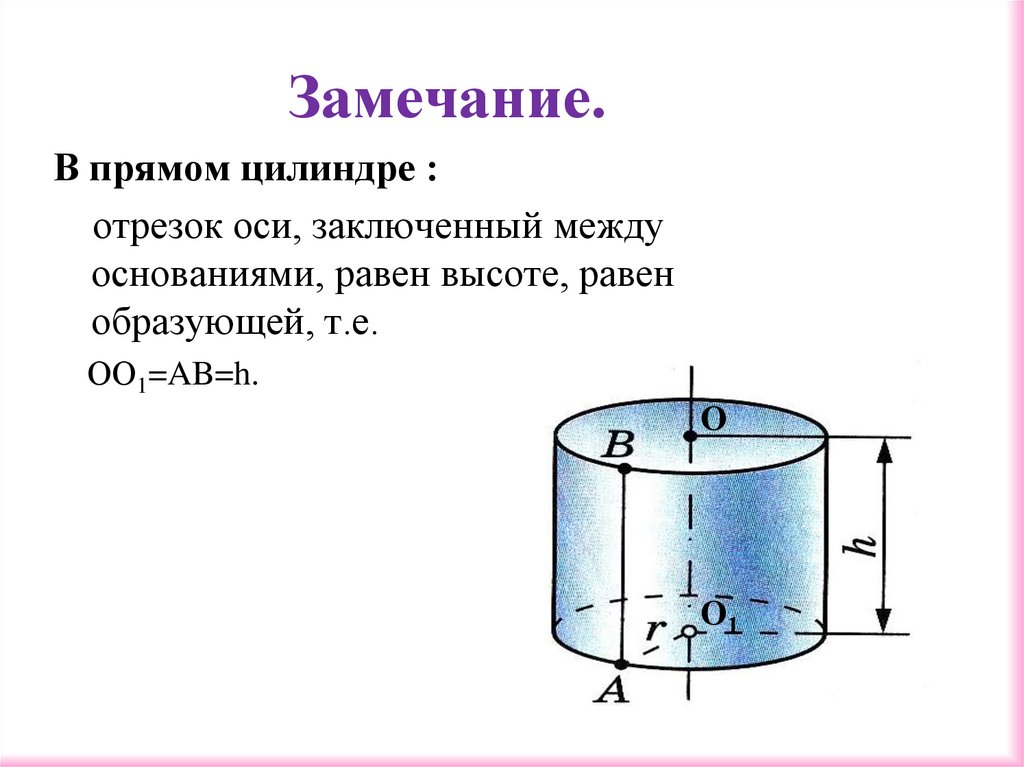
Замечание.
В прямом цилиндре :
отрезок оси, заключенный между
основаниями, равен высоте, равен
образующей, т.е.
ОО1=AB=h.
O
O1

14. Сечения.

A
B Если секущая плоскость проходит через ось
цилиндра, то сечение представляет собой
прямоугольник(ABCD).
D
C
E
L
N
K
Если секущая плоскость параллельна оси
цилиндра, то сечением является
прямоугольник(ENKL).

15.

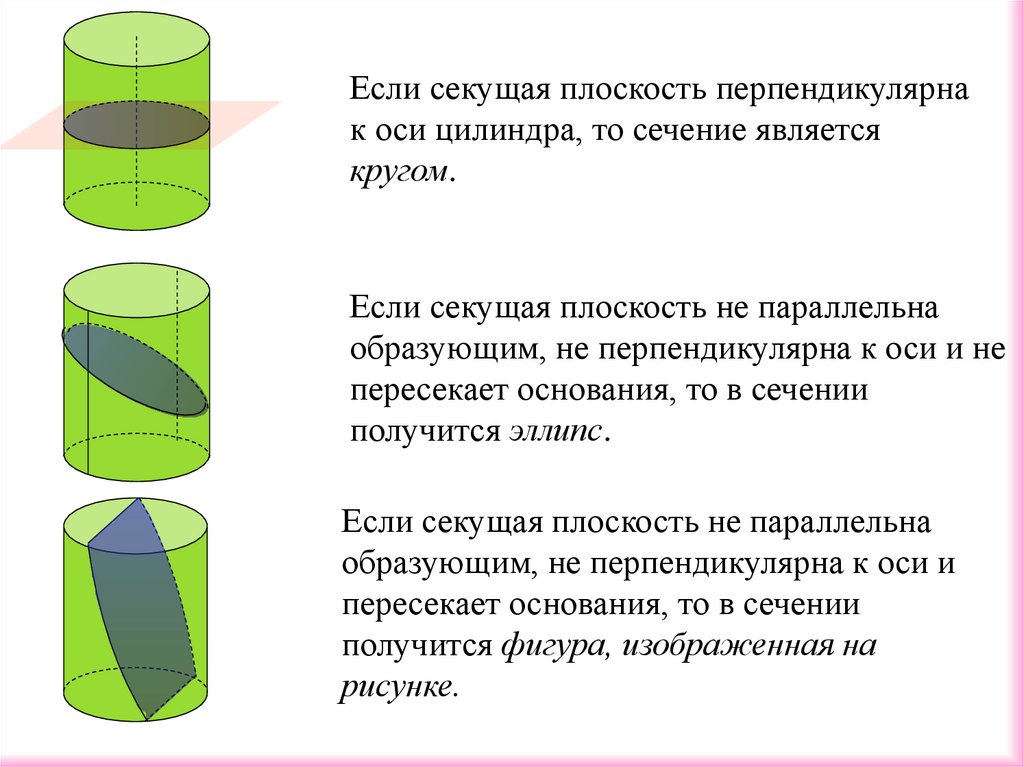
Если секущая плоскость перпендикулярна
к оси цилиндра, то сечение является
кругом.
Если секущая плоскость не параллельна
образующим, не перпендикулярна к оси и не
пересекает основания, то в сечении
получится эллипс.
Если секущая плоскость не параллельна
образующим, не перпендикулярна к оси и
пересекает основания, то в сечении
получится фигура, изображенная на
рисунке.

16. Площадь поверхности цилиндра.

Представим, что цилиндр разрезали по образующей АВ. В результате
получится прямоугольник АВВ´А´. Этот прямоугольник называется
развёрткой боковой поверхности цилиндра.
Основание АА´ прямоугольника является разверткой окружности цилиндра =>
АА´=2πR; высота АВ – образующая цилиндра => АВ=h.
За площадь боковой поверхности цилиндра принимают площадь её
развёртки.
Т. к. SАВВ´А´=АА´·AB=2πrh, то для вычисления площади Sбок. боковой
поверхности цилиндра получается формула
Sбок.=2πrh
Площадь полной поверхности.
Площадь полной поверхности цилиндра - это сумма площадей боковой
поверхности и двух оснований.
Sполн.=2πR(R+h).

17.

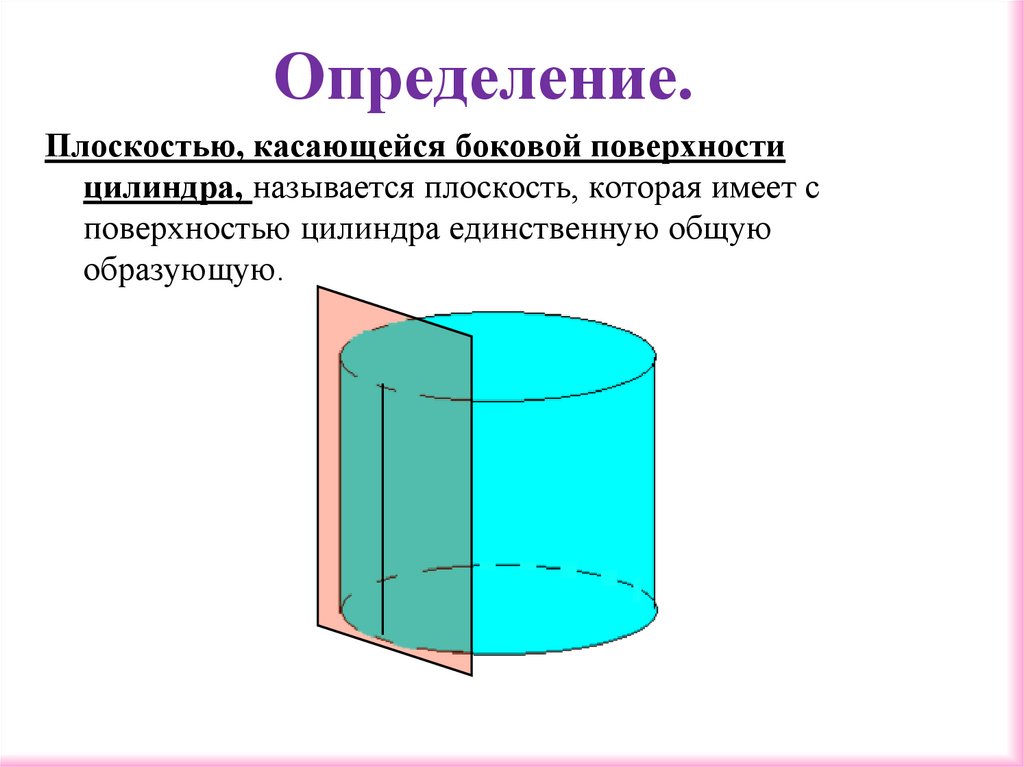
Определение.
Плоскостью, касающейся боковой поверхности
цилиндра, называется плоскость, которая имеет с
поверхностью цилиндра единственную общую
образующую.

18. Опорная плоскость.

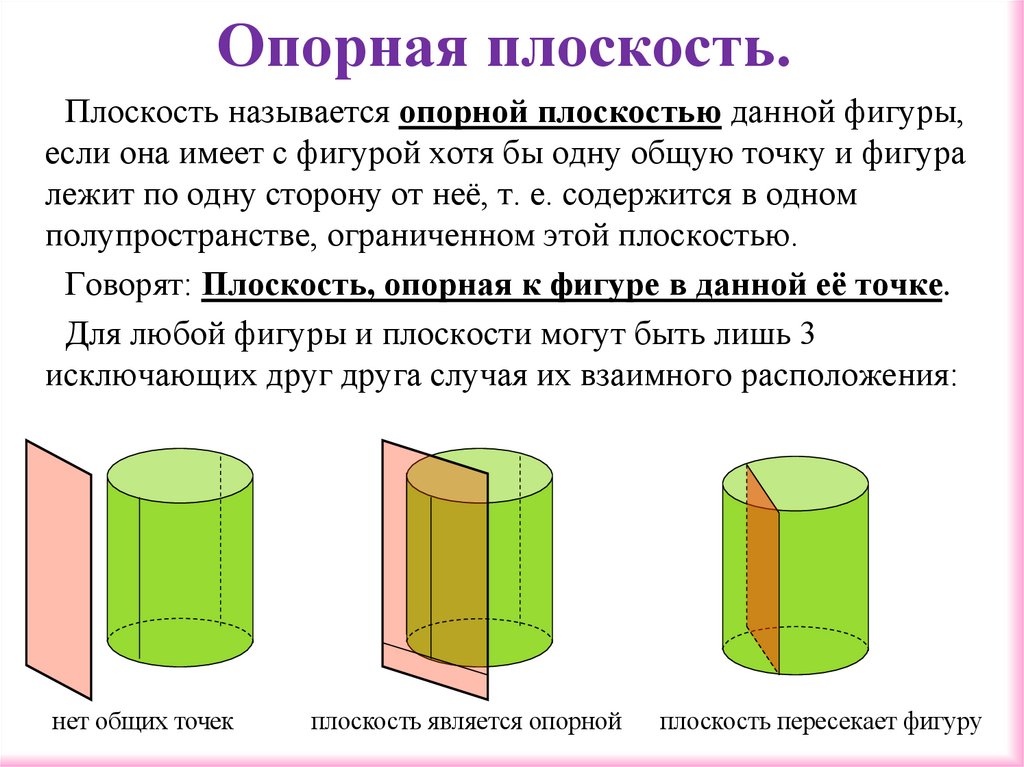
Плоскость называется опорной плоскостью данной фигуры,
если она имеет с фигурой хотя бы одну общую точку и фигура
лежит по одну сторону от неё, т. е. содержится в одном
полупространстве, ограниченном этой плоскостью.
Говорят: Плоскость, опорная к фигуре в данной её точке.
Для любой фигуры и плоскости могут быть лишь 3
исключающих друг друга случая их взаимного расположения:
нет общих точек
плоскость является опорной
плоскость пересекает фигуру

19. Вписанный и описанный цилиндр.

20. Вписанный в призму и описанный около неё цилиндр.

Определение.
Призма называется вписанной в цилиндр, если
основания её равные многоугольники, вписанные в
основания цилиндра, а боковые рёбра являются
образующими цилиндра.
___________________________________________
Определение.
Призма называется описанной около цилиндра,
если основания её - это многоугольники,
описанные около оснований цилиндра, а боковые
грани касаются цилиндра.

21. Вписанный в сферу и описанный около неё цилиндр.

Сфера называется вписанной в цилиндр, если она касается
его оснований и боковой поверхности (касается каждой
образующей).
Иначе.
Сфера называется вписанной в цилиндр, если она касается
его оснований, а с боковой поверхностью цилиндра имеет
общую окружность.
Теорема.
►Сферу можно вписать только в такой цилиндр, высота
которого равна диаметру основания.
Цилиндр называется вписанным в сферу, если окружности
оснований цилиндра лежат на сфере. При этом сфера
называется описанной около цилиндра.
Шар называется описанным около цилиндра, если
основания цилиндра служат сечениями шара.

22. Вписанный в конус и описанный вокруг него цилиндр.

Цилиндр называется вписанным в конус, если
одно из его оснований имеет с конусом общую
окружность, а другое основание лежит на
основании конуса.
Конус называется вписанным в цилиндр, если
его основание совпадает с одним из оснований
цилиндра, а вершина конуса лежит на другом
основании цилиндра.

23. Вписанный в пирамиду и описанный около неё цилиндр.

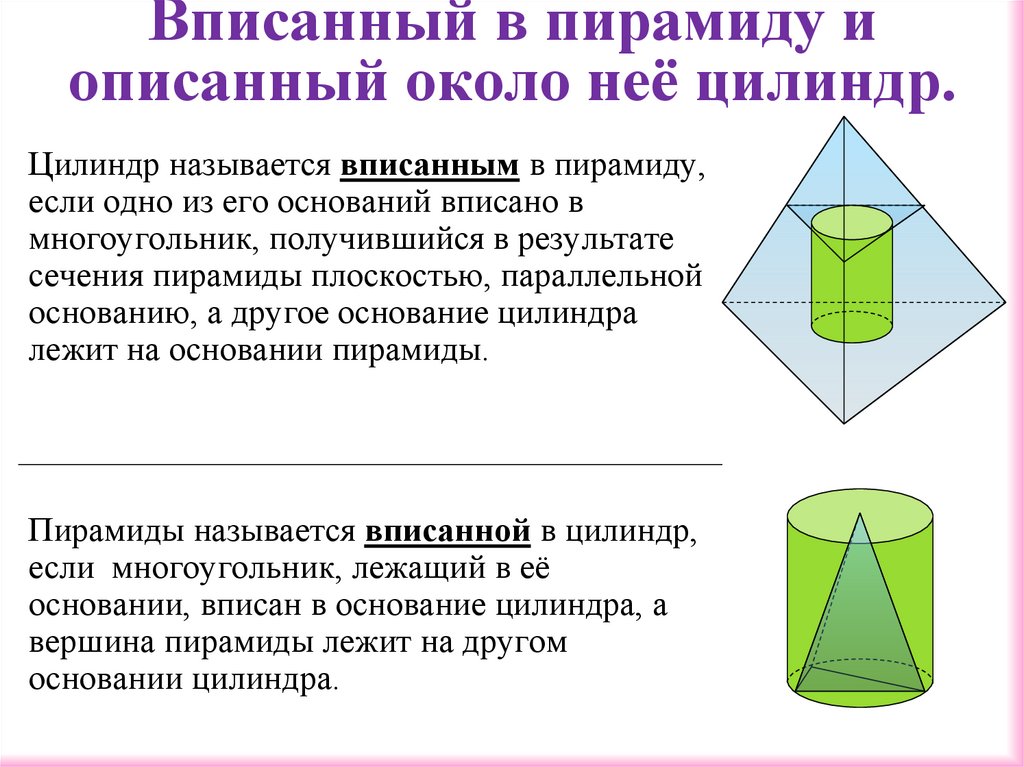
Цилиндр называется вписанным в пирамиду,
если одно из его оснований вписано в
многоугольник, получившийся в результате
сечения пирамиды плоскостью, параллельной
основанию, а другое основание цилиндра
лежит на основании пирамиды.
Пирамиды называется вписанной в цилиндр,
если многоугольник, лежащий в её
основании, вписан в основание цилиндра, а
вершина пирамиды лежит на другом
основании цилиндра.

24. Объем цилиндра.

Теорема.
Объём цилиндра равен произведению площади
основания на высоту.
Дано: цилиндр P, r – радиус основания, h –
высота.
Доказать: V=Sосн.h

25.

Доказательство:
Впишем в данный цилиндр P радиуса r и высоты
h правильную n-угольную призму Fn, а в эту
призму впишем цилиндр Pn. Обозначим через V
и Vn объёмы цилиндров P и Pn, через rn радиус
цилиндра Pn. Так как объем призмы Fn равен Sn·h,
где Sn – площадь основания призмы, а цилиндр P
P содержит призму Fn, которая, в свою очередь, содержит цилиндр
Pn, то Vn< Sn·h <V (1). Будем неограниченно увеличивать число n.
При этом радиус rn цилиндра Pn стремится к радиусу r цилиндра P
1800
rn r cos
r при n
n
. Поэтому объем цилиндра Pn стремится к
объему цилиндра P: lim V V. Из неравенств(1) следует, что и lim S h V
n
n
n
Но lim S r Таким образом, V=πr²h (2). Обозначив площадь π·r²
основания цилиндра буквой Sосн., из формулы (2) получим
2
n
n
V=Sосн.·h
n

26. Отрезок цилиндра.

Отрезком цилиндра, или цилиндрической подковкой,
называют часть цилиндра, отсекаемую плоскостью,
пересекающей одно основание цилиндра и заключенную
между этим основанием и секущей плоскостью.
Высотой отрезка цилиндра называют наибольшую из
образующих CD=H; AB=2a прямое ребро, CE=b – стрелка
сегмента основания, α – центральный угол основания в
радианах.
Боковая поверхность отрезка цилиндра
S бок.
RH
2a b R
b
D
Объем отрезка цилиндра
B
H
E
H
V
2a 3R 2 a 2 3R 2 b R
6b
C
A
α O

27. Цилиндрическая труба.

Цилиндрической трубой (полым цилиндром) называют
тело, ограниченное двумя цилиндрическими круговыми
поверхностями с общей осью и различными радиусами и
двумя параллельными плоскостями, перпендикулярными
образующим.
R и r – внешний и внутренний радиусы; δ=(R-r) – толщина
R
цилиндрической трубы, ρ=½(R+r) – средний радиус.
r
Боковая поверхность цилиндрической трубы
Sбок.=2πH(R+r).
Полная поверхность
Sполн.=2π(R+r)(H+R-r)=4πρ(H+δ)
и объем
V=πH(R²-r²)=2πHρδ
Н

28. Подобные цилиндры.

Два цилиндра называются подобными, если подобны их
осевые сечения.
Теорема.
Боковые и полные поверхности подобных цилиндров
относятся как кубы их сходственных линейных элементов
(радиусов оснований, высот, образующих).
P1
P
h
h1
r
r1
Sбок.P Sполн.P r 3 h3
3 3
Sбок.P1 Sполн.P1 r1 h1

29. Усеченный цилиндр.

Усечённый цилиндр - геометрическое тело, отсекаемое от
цилиндра плоскостью, непараллельной основанию и не
пересекающей его.
Боковая поверхность усеченного цилиндра
Sбок. R H1 H 2
Полная поверхность
2
H
H
1
S полн. R R H1 H 2 R 2 2
2
Объём круглого усеченного цилиндра равен
h1 h2
V r
2
2

30.

Другие виды
цилиндра.

31.

Определение.
Эллиптический цилиндр - линейчатая
цилиндрическая поверхность, уравнение которой
может быть приведено к виду
x2 y2
2 1
2
a
b

32.

Определение.
Гиперболическим цилиндром называется
поверхность, которая в некоторой декартовой системе
координат задаётся уравнением
x2 y2
2 1
2
a
b

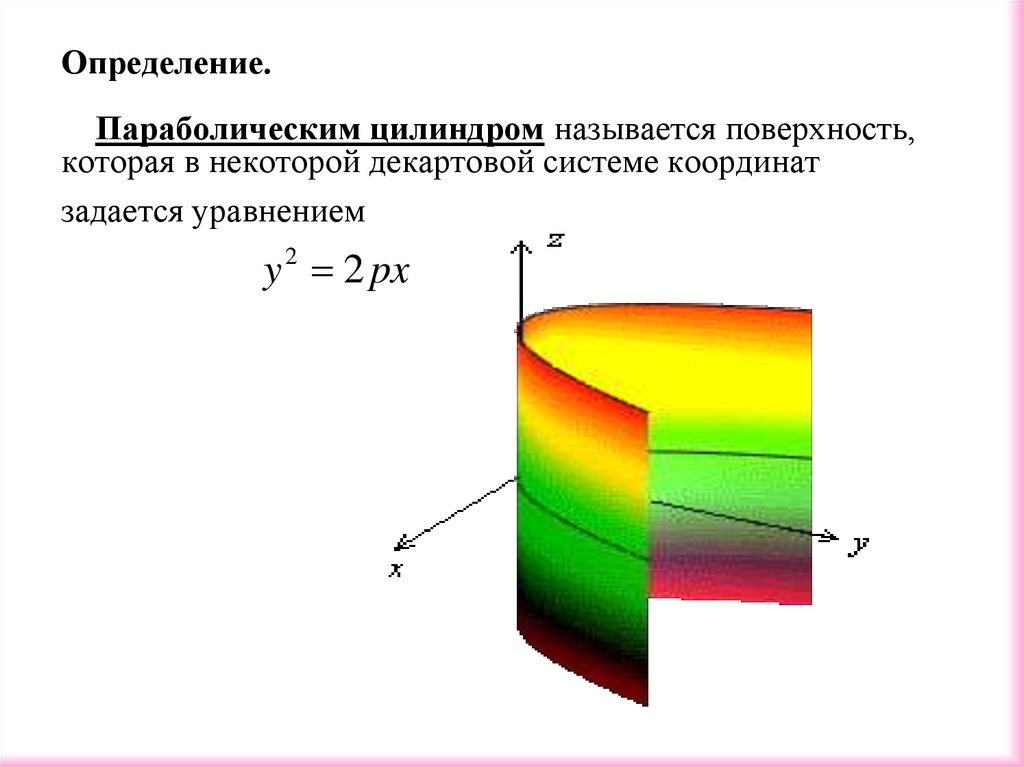
33. Определение. Параболическим цилиндром называется поверхность, которая в некоторой декартовой системе координат задается

уравнением
y 2 2 px

34. Круговой цилиндр вдоль пространственной кривой.

Спиральный цилиндр.

35. Винтовая линия.

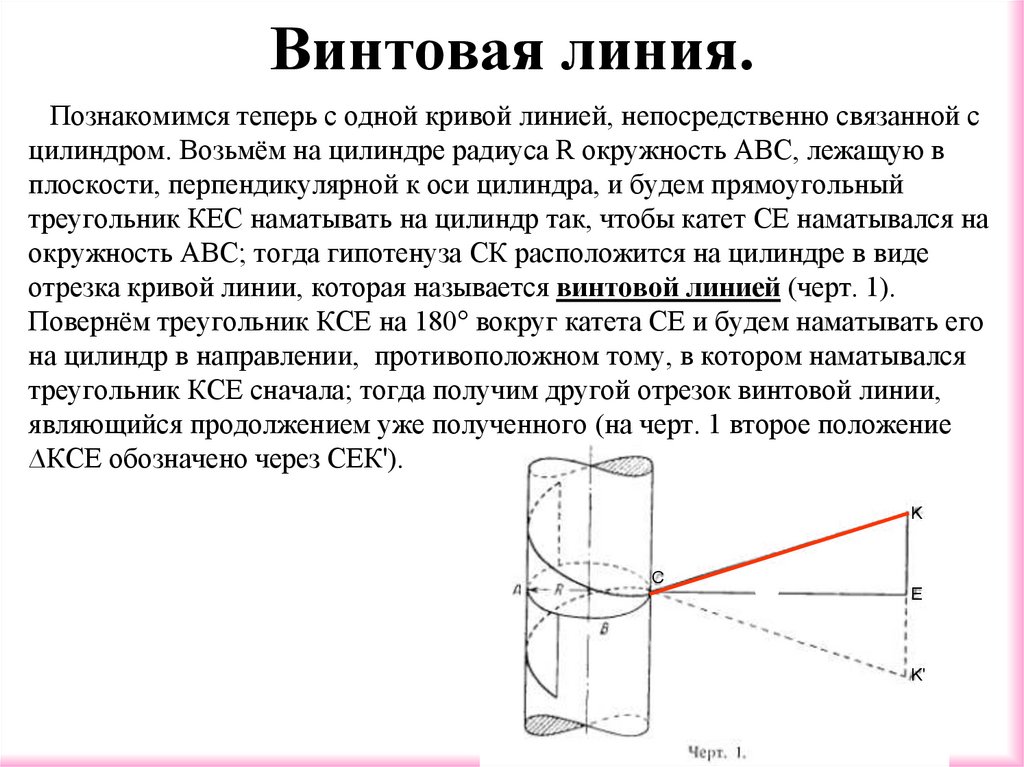
Познакомимся теперь с одной кривой линией, непосредственно связанной с
цилиндром. Возьмём на цилиндре радиуса R окружность ABC, лежащую в
плоскости, перпендикулярной к оси цилиндра, и будем прямоугольный
треугольник КЕС наматывать на цилиндр так, чтобы катет СЕ наматывался на
окружность ABC; тогда гипотенуза СК расположится на цилиндре в виде
отрезка кривой линии, которая называется винтовой линией (черт. 1).
Повернём треугольник КСЕ на 180° вокруг катета СЕ и будем наматывать его
на цилиндр в направлении, противоположном тому, в котором наматывался
треугольник КСЕ сначала; тогда получим другой отрезок винтовой линии,
являющийся продолжением уже полученного (на черт. 1 второе положение
∆КСЕ обозначено через СЕК').
K
C
E
K'

36.

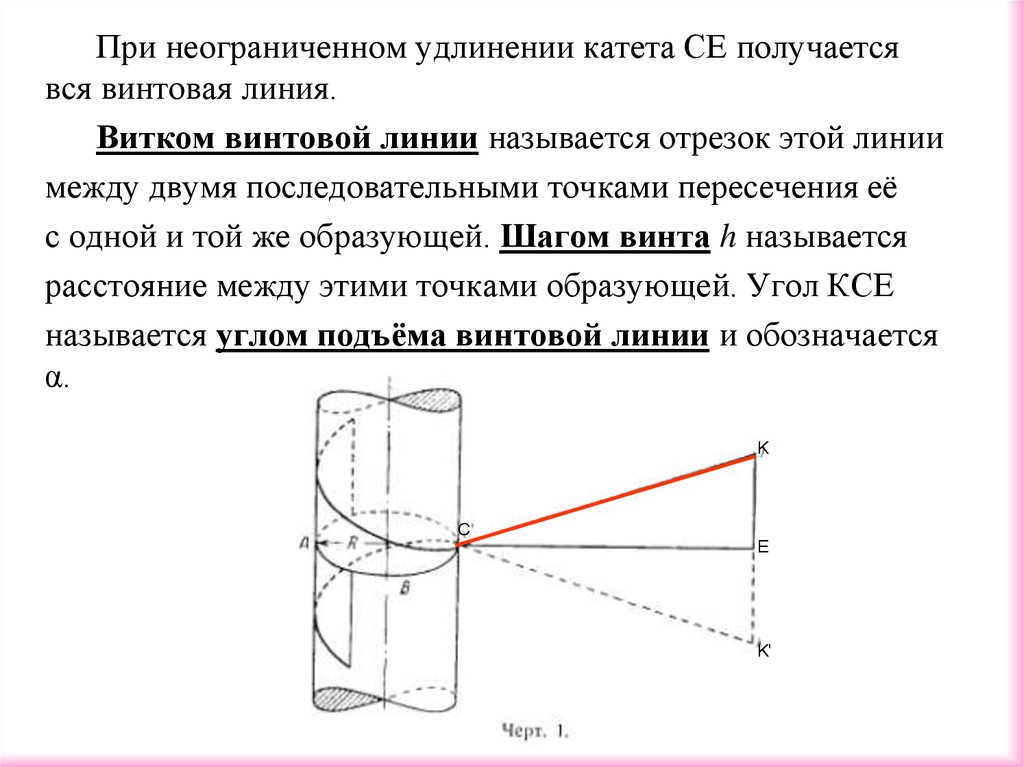
При неограниченном удлинении катета СЕ получается
вся винтовая линия.
Витком винтовой линии называется отрезок этой линии
между двумя последовательными точками пересечения её
с одной и той же образующей. Шагом винта h называется
расстояние между этими точками образующей. Угол КСЕ
называется углом подъёма винтовой линии и обозначается
α.
K
C
E
K'

37.

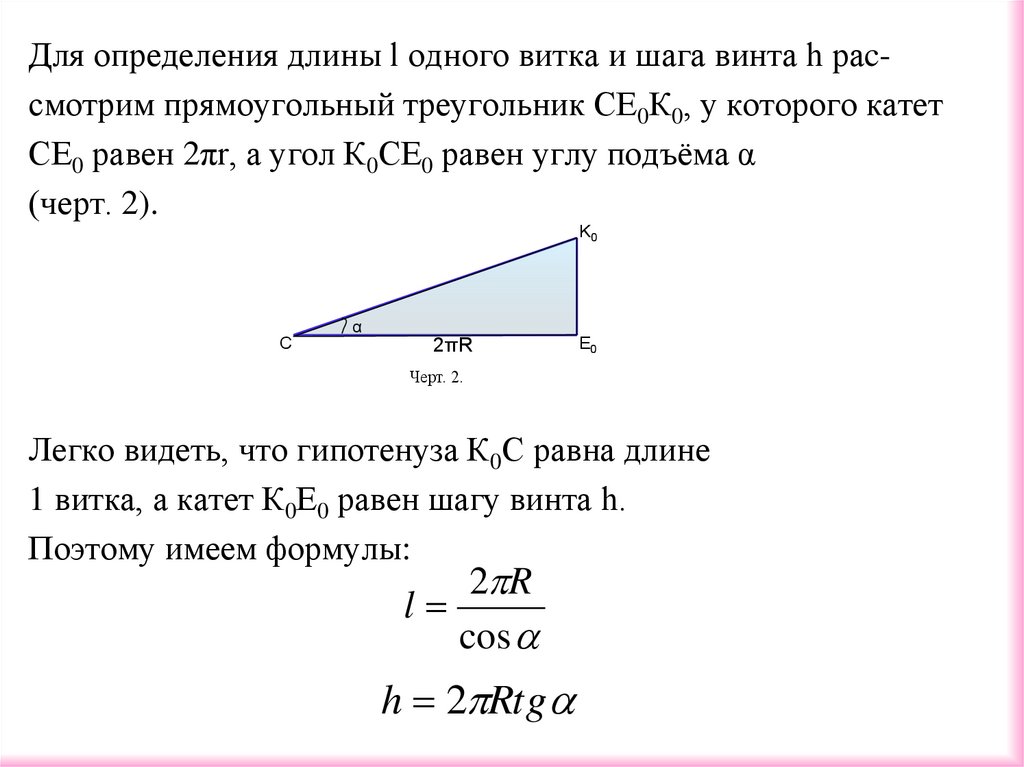
Для определения длины l одного витка и шага винта h раcсмотрим прямоугольный треугольник СЕ0К0, у которого катет
СЕ0 равен 2πr, а угол К0СЕ0 равен углу подъёма α
(черт. 2).
K0
α
C
2πR
E0
Черт. 2.
Легко видеть, что гипотенуза К0С равна длине
1 витка, а катет К0Е0 равен шагу винта h.
Поэтому имеем формулы:
2 R
l
cos
h 2 Rtg

38.

Винтовые линии бывают правовинтовые и левовинтовые.
Предположим, что по винтовой линии движется точка.
Проекцией винтовой линии на плоскость, перпендикулярную к
её оси (будем называть осью винтовой линии ось цилиндра, на
котором она расположена), будет, очевидно, окружность.
Поэтому если смотреть на винтовую линию в направлении её
оси, то будет казаться, что точка движется по окружности.
Если точка движется по окружности по часовой стрелке,
удаляясь от нас, то винтовая линия называется правовинтовой, если же она движется по часовой стрелке,
приближаясь к нам, то винтовая линия называется левовинтовой. Правовинтовую и левовинтовую линии на одном и
том же цилиндре с одинаковым углом подъёма совместить
нельзя. На черт.1 у нас получилась левовинтовая линия;
чтобы получить правовинтовую линию, нужно наматывать
треугольник в противоположном направлении.