Динамические характеристики системы точечных масс

1. Лекция 17-2016

Динамические характеристики
системы точечных масс
1

2.

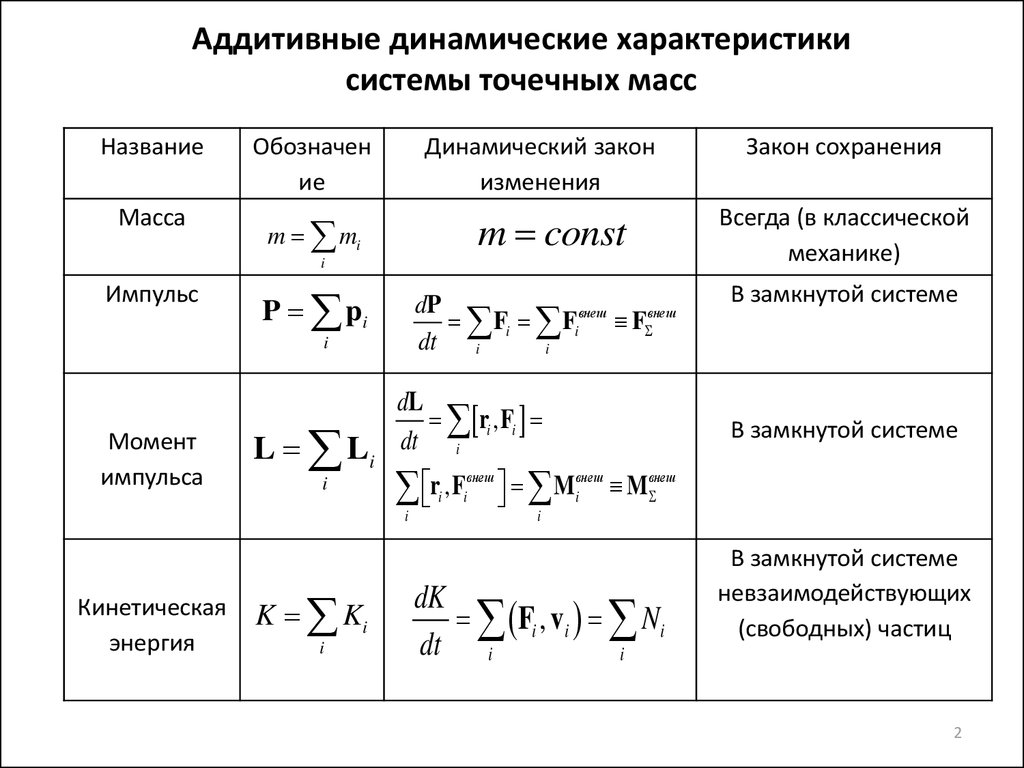
Аддитивные динамические характеристики
системы точечных масс
Название
Обозначен
ие
Масса
m mi
Динамический закон
изменения
m const
Всегда (в классической
механике)
dP
Fi Fiвнеш F внеш
dt
i
i
В замкнутой системе
i
Импульс
P pi
i
Момент
импульса
L Li
i
dL
ri , Fi
dt i
K Ki
i
В замкнутой системе
внеш
внеш
внеш
r
,
F
M
M
i i i
i
Кинетическая
энергия
Закон сохранения
i
dK
Fi , vi Ni
dt i
i
В замкнутой системе
невзаимодействующих
(свободных) частиц
2

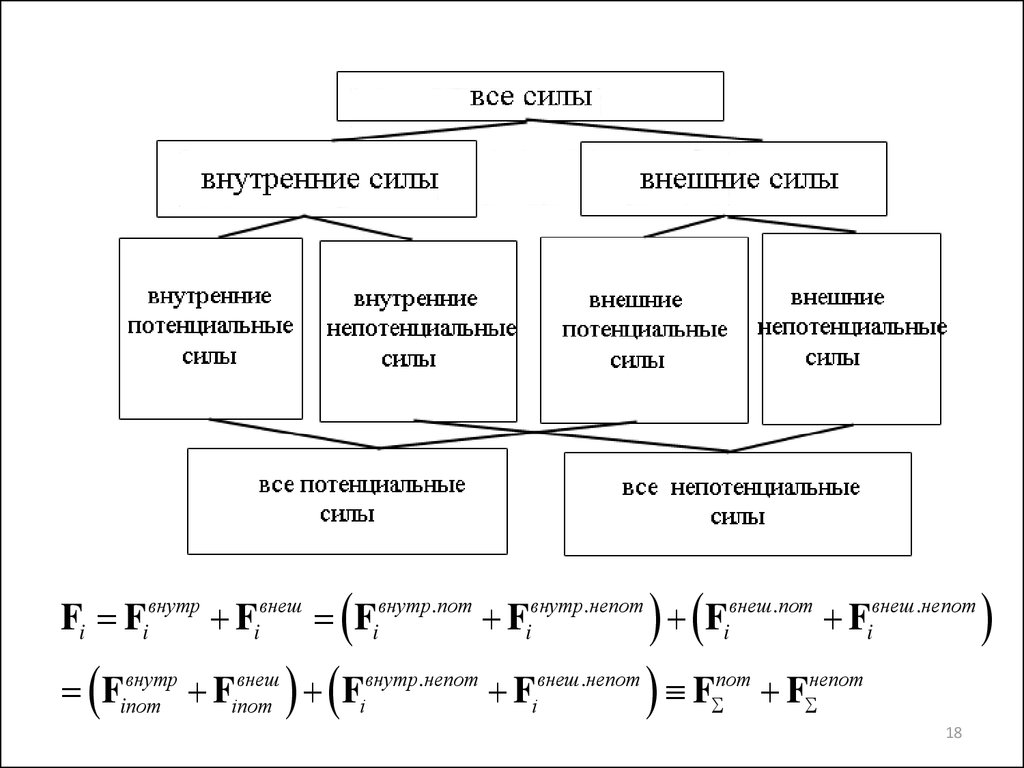
3. Внутренние и внешние силы. Внутренние и внешние моменты сил. Полная взаимная нейтрализация внутренних сил

Все силы, действующие на каждую частицу, разделяем на две категории:
внутренние силы, порождаемые взаимодействием
выделенной частицы с
остальными частицами системы и внешние силы, порождаемые взаимодействиями с
телами, не входящими в систему:
внеш
внеш
Fi Fiвнутр
F
F
F
ik i .
i
i k
В силу третьего закона Ньютона:
внутр
F
i
i
1
Fik Fki 0
2 i ,k i
Fi Fiвнеш
.
3

4. Внутренние и внешние моменты сил. Полная взаимная нейтрализация внутренних моментов сил

M M i ri , Fi ri , Fiвнутр ri , Fiвнеш M iвнутр M iвнеш
i
i
i
i
i
i
Разобьем все частицы системы на взаимодействующие пары и вычислим
суммарный момент сил взаимодействия каждой пары
внутр
M
i
i
1
Mik M ki ;
2 i ,k
M ik M ki ri , Fik rk , Fki ri rk , Fik 0;
M Miвнеш
i
Суммарный момент импульса всех сил, действующих на все частицы равен векторной
сумме моментов внешних сил, действующих на каждую частицу системы.
4

5. Динамические законы изменения полного импульса системы и полного момента импульса системы

Изменение полного импульса системы равно сумме всех внешних сил,
действующих на систему, а изменение полного момента импульса системы
равно сумме моментов всех внешних сил, действующих на частицы системы
dP
внеш
внеш
Fi Fi F ;
dt
i
i
dL
внеш
внеш
внеш
ri , Fi ri , Fi Mi M
dt
i
i
i
5

6. Законы сохранения полного импульса системы и полного момента импульса системы

При движении замкнутой системе материальных частиц вектор полного
импульса и
вектор
полный момент импульса системы относительно
неподвижного полюса остаются неизменными.
P(t ) P(0); L(t ) L(0)
Если проекция суммы всех внешних сил на некоторое направление равна нулю,
то в процессе движения всех частиц системы остается неизменной (сохраняется)
проекция импульса системы на данное направление:
F
внеш
l
0 Pl const
Если сумма моментов всех внешних сил, относительно некоторой оси равна
нулю, то в процессе движения всех частиц системы остается неизменной
(сохраняется) момент импульса системы относительно этой оси:
M
внеш
l
0 Ll const
6

7.

Внутренние силы не могут сдвинуть систему как целое и не могут повернуть
систему как целое. Внутренние силы, подчиняющиеся третьему закону
Ньютона, способны изменить только относительные расстояния между
частицами и относительные скорости движения частиц.
7

8. Изменении полной кинетической энергии системы

dK i
dK
Fi , v i Fi внутр Fiвнеш , v i N iвнут N iвнеш N ;
dt
dt
i
i
i
i
i
t2
t2
K K 2 K1 Fi внутр , v i dt Fiвнеш , v i dt
i
ri 2
F
внутр
i
i
ri 1
i
t1
t1
ri 2
внеш
, dri Fiвнеш , dri A1внутр
A
2
1 2
i
ri 1
Скорость изменения кинетической энергии системы равна мощности всех сил,
действующих на все частицы системы. Изменение кинетической энергии при
перемещении всех частиц системы из начального положения в конечное положение
равно работе всех сил, действующих на все частицы системы при данном перемещении.
Таким образом, любая сила, как внутренняя, так и внешняя, способная совершить
механическую работу, может изменить полную кинетическую энергию всей
системы.
8

9. Центр масс (центр инерции) системы

Механическая
характеристика
Положение
скорость
импульс
Обозначение
Rc
Vc
Pc
Определение
mi
R c ri
m
i
mi dri
Vc
i m dt
mi
vi
i m
Pc mVc mi vi pi P
i
i
Импульс центра масс равен полному импульсу всей системы
9

10. Представление полного момента импульса системы как суммы собственного и орбитального моментов.

L L Lc
L ri , p i , LC R c , P
i
Полный момент импульса системы относительно неподвижного полюса
равен сумме момента импульса системы относительно центра масс L
(собственного момента импульса)и момента импульса самого центра масс
относительно данного полюса L C (орбитального момента импульса)
L Li ri , p i ri R c , p i mi ri , v i R c , p i
i
i
i
i
mi ri , v i Vc R c , P ri , mi v i miri , Vc R c , P
i
i
i
ri , p i M R c , Vc R c , P ri , p i R c , P L L C
i
i
i
10

11.

При рассмотрении системы с расстояний значительно превышающие ее
размер, классическая система превращается в материальную точку, момент
импульса которой равен ее орбитальному моменту.
Для квантовой частицы собственный момент импульса не обращается в
нуль, а переходит в механическую характеристику, называемую спином
частицы ( от анг. spin - веретено).
Проекция спина на любую ось кратна величине постоянной Дирака:
h
1, 054571628 10 34 Дж×с
2
Размерность момента импульса совпадает с размерностью действия:
L масса длина скорость энергия время
11

12. Теорема Кенига

Полная кинетическая энергия системы равна сумме ее собственной
кинетической энергии и кинетической энергии центра масс:
2
2
mi vi mVc
K
K KC
2
2
i
mi
mi
K v i , v i v i Vc , v i Vc
2
2
i
i
mi
mi
i 2 v i , v i i 2 Vc , Vc i mi v i , Vc
mi v i 2 mVc2
i 2 2 Pc , Vc K KC
12

13.

Силы, придающие одинаковое ускорение всем
частицам системы
1. Согласно второму закону Ньютона, такие силы должны быть
пропорциональны массе частицы.
2. Такие силы не могут изменить момента импульса относительно любой
оси, проходящей через центр масс механической системы
M ri , fi ri , mi a mi ri , a mi ri , a
i
i
i
i
mR c , a R c , ma R c , mi a ;
i
m mi полная масса системы
i
Примеры таких сил:
1. Однородное поле силы тяжести
2. Сила инерции поступательного движения системы
13

14.

При удалении от системы на достаточно большое
расстояние ее внутренние движения становятся
незаметными; система превращается в материальную
точку, обладающую кинетической энергией, равной
кинетической энергии центра масс.
Таким образом, отвлекаясь от внутренней жизни
механической системы, мы можем ее представить как
материальную точку, механические характеристики
которой (положение, импульс, момент импульса и
кинетическая энергия) определяются соответствующими
характеристиками центра масс системы.
14

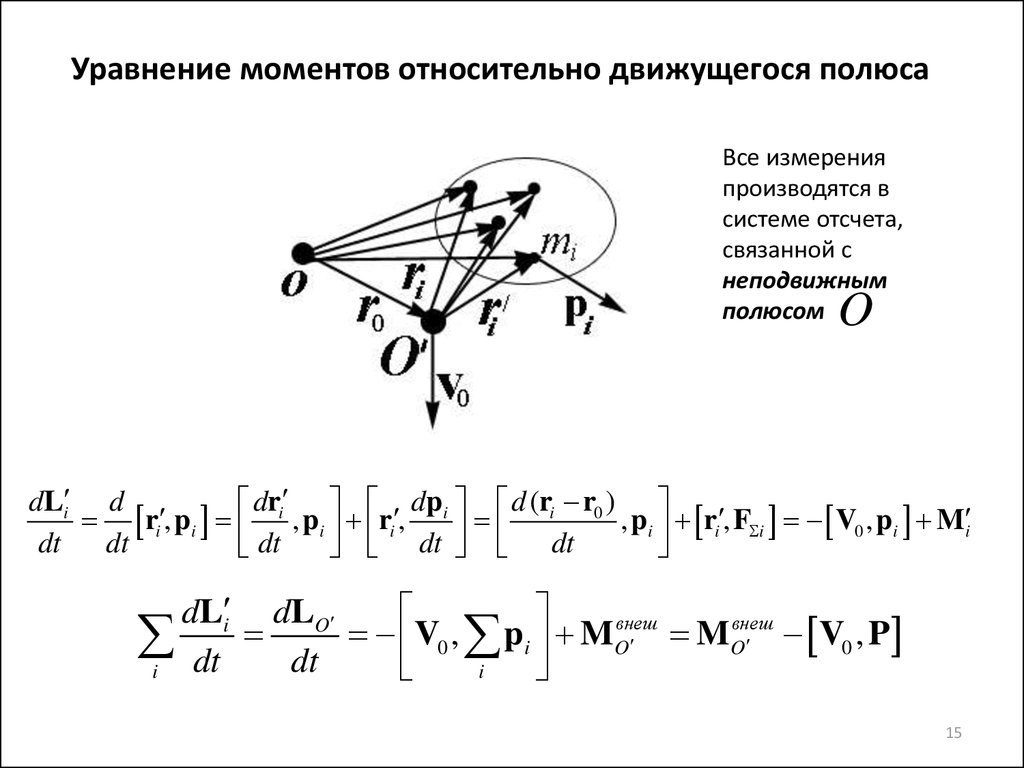
15. Уравнение моментов относительно движущегося полюса

Все измерения
производятся в
системе отсчета,
связанной с
неподвижным
полюсом
O
dL i d
dri dpi d (ri r0 )
ri , pi , pi ri ,
, pi ri , F i V0 , pi M i
dt
dt
dt
dt dt
dL i dLO
внеш
внеш
V
,
p
M
M
V0 , P
i dt dt
O
O
0 i
i
15

16.

Случаи, в которых уравнение моментов относительно
движущегося полюса, совпадает с уравнением моментов
относительно неподвижного полюса
dLO
M Oвнеш
dt
1. Движущейся полюс совпадает с центром масс системы:
V0 VC
При вычислении кинетического момента можно заменить скорости движения
частиц в лабораторной системе их скоростями в системе центра масс:
LO ri , mi ( v i VC ) L mi v i , VC L mPC , VC L .
i
2. Скорость движущегося полюса параллельна скорости центра масс системы
V0 VC
При вычислении кинетического момента относительно движущегося полюса
необходимо брать скорости в системе отсчета неподвижного полюса ( в
исходной лабораторной системе отсчета).
16

17. Потенциальная энергия механической системы Внутренняя потенциальная энергия системы.

Внутренняя потенциальная энергия системы – потенциальная
внутренних сил, действующих между частицами системы.
энергия
Внутренние силы, подчиняющиеся третьему закону Ньютона действуют вдоль
относительных расстояний между частицами. Поэтому эти силы не способны
повернуть эти расстояния, а могут только изменить их величину.
Работа, совершаемая силами взаимодействия между произвольной парой частиц:
Aik Fik , drk Fki , dri Fik , drk dri Fik , d (rk ri ) Fik d rik ;
Aвнутр
1
1
F
d
r
Fir drik
ik
ik
2 i k
2 i k
Внутренние взаимодействия способны изменить энергию тела только за
счет создаваемых ими деформаций тела dr 0
ik
В абсолютно твердом теле суммарная работа внутренних сил всегда равна нулю,
поскольку в таком теле относительные расстояния между частицами не изменяются.
17

18.

Fi Fiвнутр Fiвнеш Fiвнутр.пот Fiвнутр.непот Fiвнеш.пот Fiвнеш.непот
внутр
внеш
внутр .непот
внеш .непот
пот
непот
Fiпот
Fiпот
F
F
F
F
i
i
18

19. Внутренние потенциальные силы

Внутренние потенциальные силы – это силы взаимодействия между частицами
системы, суммарная работа которых не зависит от способа изменения
конфигурации системы.
Конфигурацией системы материальных точек называется фиксированное
взаимное расположение всех точек, образующих систему.
Различные способы изменения конфигурации системы предполагают:
1.Различный порядок перемещения частиц;
2. Различные траектории перемещения частиц их заданных начальных положений
в заданные конечные положения;
3. Одновременное перемещение всех частиц или последовательное их
перемещение.
Внутренняя потенциальная энергия данной конфигурации системы равна работе
всех внутренних потенциальных сил при перемещении частиц системы из данной
конфигурации в конфигурацию, в которой частицы бесконечно удалены друг от
друга:
U внутр Fiвнутр.пот , dri
i
ri
19

20. Потенциальная энергия заданной конфигурации системы

Потенциальная энергия заданной конфигурации системы определяется как
суммарная работа потенциальных сил (внешних и внутренних) по переводу
системы в конфигурацию, для которой потенциальная энергия принята равной
нулю (обычно – система частиц, удаленных друг от друга и от внешних тел на
бесконечность):
U (r1 , r2 ,...rN ) F
пот
i
i
F
пот
i
ri
i
ri
, dri F
внутр .пот
i
i
, dri Fiвнеш.пот , dri
i
ri
ri
, dri Fiвнутр.пот , dri Fiвнеш.пот , dri U внутр. U внеш.
ri
i
ri
i
Потенциальные внутренние силы приводят к возникновению упругих деформаций
в теле, тогда как непотенциальные внутренние силы приводят к возникновению
неупругих деформаций.
Внутренней потенциальной энергией обладает тело, испытывающее упругую
деформацию. Внешняя потенциальная энергия возникает в теле за счет воздействия
на него внешних потенциальных сил.
Абсолютно твердое тело обладает только внешней потенциальной энергией, когда
под действием внешних сил оно смещается как целое.
20

21. Полная механическая энергия системы

W K U Ki U (r1 , r2 ,...rN )
i
t2
t2
K K 2 K1 Fi внутр , v i dt Fiвнеш , v i dt
i
ri 2
F
внутр
ri 2
F
i
t1
ri1
i
t1
t2
внутр .непот
i
i
t2
, dri Fiвнеш , dri Fi внутр.пот , dri Fiвнеш.пот , dri
i
ri 1
t1
ri 2
t2
i
i
i
t1
, dri Fiвнеш.непот , dri
i
ri 1
t1
ri 2
t2
U1 U 2 Fi внутр.непот , dri Fiвнеш.непот , dri
i
ri 1
i
t1
Убыль полной потенциальной энергии системы при движении системы равна
работе всех потенциальных сил при перемещении системы из начального
положения в конечное.
21

22. Законы сохранения механической энергии системы

Законы сохранения полной механической энергии системы
W W2 W1 ( K 2 U 2 ) ( K1 U1 )
ri 2
F
i
i
ri 1
ri 2
внут.непот
ri 2
, dri Fi внеш.непот , dri Fi непот , dri
i
i
ri 1
ri 1
Полная энергия системы сохраняется в отсутствие диссипативных сил,
действующих как внутри системы, так и со стороны внешних тел.
Внутренняя механическая энергия системы равна сумме полной
кинетической энергии системы
и потенциальной энергии
взаимодействия частиц системы между собой
Wо K U внутр (r1 , r2 ,...rN ) K Fiвнутр.пот , dri
i
ri
22

23. Законы сохранения механической энергии замкнутой системы

В замкнутой системе внешние силы отсутствуют и полная механическая
энергия системы равна ее собственной энергии:
W Wо
Изменение собственной энергии системы при ее движении равно сумме
работ внутренних диссипативных сил, т.е. при создании в теле неупругих
деформаций:
ri 2
W Wo Wo 2 Wo1 Fi
i
внут.непот
, dri
ri 1
В замкнутой системе собственная энергия сохраняется в
отсутствие внутренних диссипативных сил, т.е. в отсутствие в
теле неупругих деформаций
23

24. Законы сохранения энергии абсолютно твердого тела

В модели АТТ
Aвнут.пот U внутр (r1 , r2 ,...rN ) 0;
ri 2
Aвнут.непот Fi внут.непот , dri 0
i
ri 1
Внутренняя механическая энергия абсолютно твердого тела определяется
только его кинетической энергией:
Wo K
Изменение кинетической энергии АТТ может иметь место только в присутствие
внешних сил:
K Aвнеш.пот Aвнеш.непот A внеш
Изменение полной механической энергии твердого тела возможно только в
присутствие внешних непотенциальных сил:
ri 2
W Aвнеш.непот Fi внеш.непот , dri
i
ri 1
24