Физические основы механики. Принцип относительности в механике. Лекция 3 (часть I)

1. Физические основы механики

Семестр 1

2. ЛЕКЦИЯ № 3 ( часть I )

Принцип относительности в механике
1. Принцип относительности Галилея. Переход из одной инерциальной системы
отсчета в другую. Преобразования Галилея. Инвариантность уравнения движения.
2. Неприменимость принципа относительности Галилея к описанию динамики
электромагнитного поля. Опыты А. Майкельсона и Э. Морли по измерению скорости
света.
3. Основные положения специальной теории относительно-сти. Преобразования
Лоренца. Сокращение длины и замедление времени. Принцип относительности
Галилея. Общефизический принцип относительности.
4. Импульс и энергия частицы в релятивистской механике. Формула
Эйнштейна.Энергия покоя. Принцип соответствия.
5. Неинерциальные системы отсчёта. Силы инерции.
6. Релятивистская теория тяготения (общая теория относит.)

3. ЛЕКЦИЯ № 3 (часть II)

Динамика системы материальных точек
1.Система материальных точек. Центр масс (инерции).
Аддитивность массы в нерелятивистской механике.
2. Полный импульс системы материальных точек.
3. Закон сохранения импульса. Внутренние и внешние
силы.
4. Теорема о движении центра масс. Система центра масс.
5. Реактивное движение. Уравнение Мещерского.
Формулы Циолковского.

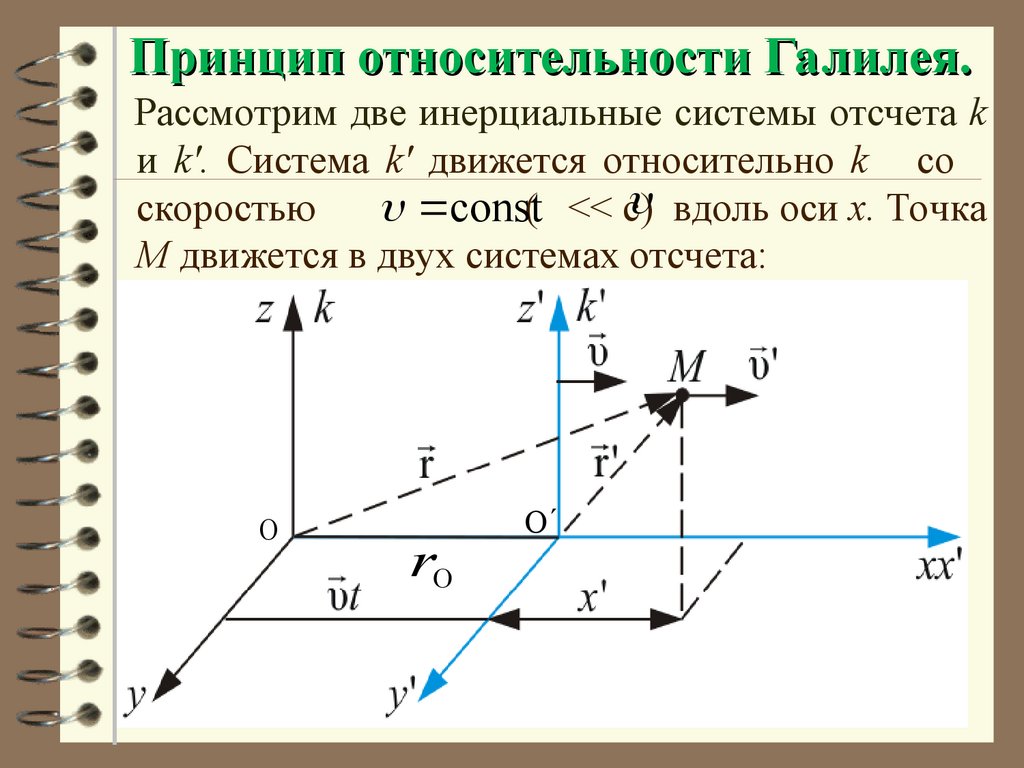
4. Принцип относительности Галилея.

Рассмотрим две инерциальные системы отсчета k
и k'. Система k' движется относительно k со
вдоль оси x. Точка
скоростью
const( << c)
М движется в двух системах отсчета:
О
r0
О

5.

Галилео Галилей
(Galileo Galilei)
Родился
15 февраля 1564
Пиза (Pisa)
Италия
Умер
8 января 1642
Арчетри (Arcetri)
Италия
астроном, философ и
физик.
важнейшие работы
улучшение телескопа
разнообразие
астрономических
наблюдений, первый закон
движения
5

6.

Запишем движение точки М в этих двух системах,
задав это движение радиус-векторами
и r
соответственно в системе k и k’ :
r'
r
r
'
r
0 положение точки
радиус-вектор,
определяющий
r0
системы
в системе отсчёта k.
О времени tk(t=t’):
К моменту
r0
Спроецировав на координатные оси, запишем
вt
скалярной форме:
x x ' t
- преобразо
y y ' вания
Галилея
z z '
t t '

7.

Продифференцируем это выражение по времени,
получим: закон сложения скоростей в классической механике (нерелятивистской механике):
dr dr '
dtили dt
'
1
Скорость движения
точки М (сигнала)
в системе kʹ
и
в системе k различны.
' 1

8.

Ускорение в системе отсчета k
d 1 d ( ) d '
а
а
dt
dt
dt
Инвариантность ускорения (одинаковость во
всех инерциальных системах отсчёта- ИСО)
Изучение медленных (
) механических
c
движений показало, что
.
=
,
m m
F F '
Таким образом, масса и сила также являются
инвариантами при переходе из одной ИСО в
другую.

9.

Уравнения движения частицы имеют одинаковый
2
2
d
r
d
r
вид во всех ИСО:
и
m
F
m
F
dt 2
dt 2
Обобщение полученных выше результатов формулируется в виде принципа относительности Галилея
(Г. Галилей, 1636 г.): законы механики одинаковы во всех
инерциальных системах отсчёта, поэтому никакими
механическими опытами внутри ИСО, изолированных
от внешних воздействий, невозможно обнаружить её
движение с постоянной скоростью. К этому принципу Г.
Галилей пришёл на основе опыта и мысленных
экспериментов. Принцип относитель-ности Галилея
утверждает равноправие всех ИСО

10. Расхождение классической теории с опытом Майкельсона - Морли.

В 1881 – 1887 гг. Альберт
Майкельсон и Эдуард Морли
экспериментально
исследовали влияние
движения Земли на скорость
распространения света,
испущенного земным
источником. Эти опыты
показали независимость
скорости света от скорости
движения источника, что
противоречит правилу
сложения скоростей в
классической механике.

11. Основные постулаты СТО (специальной теории относ)

Первый постулат теории относительности.
Все законы природы одинаковы
в инерциальных системах отсчета.
Второй постулат теории
относительности.
Скорость света c=3· м/с в вакууме
одинакова во всех инерциальных
8
системах отсчета и является 10
максимальной для любого физического
взаимодействия (сигнала).
.
Альберт
Эйнштейн
1879-1955

12. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА

Для систем отсчёта
и преобразования
k
k
Лоренца имеют вид (V ~ c) релятивистский
случай:
V
t 2 x
x Vt
x
; y y; z z ; t
c
.
2
2
1 V c
1 V 2 c2
Лоренц

13. Сокращение длины

Рассмотрим стержень, расположенный вдоль оси
xʹ и покоящийся относительно системы Kʹ. Длина
его в этой системе равна l0 x2 x1 .
Для определения длины стержня в системе K
нужно отметить координаты концов стержня в
один и тот же момент времени t.
x1
x1 Vt
2
1 V c
2
; x2
x2 x1
x2 Vt
2
1 V c
x2 x1
2
1 V c
2
.
x2 x1 l ;
l l0 1 V 2 c 2 .
2

14. Замедление времени

Пусть в одной и той же точке xʹ = xʹ = xʹ системы Kʹ происходят два
1
2
события в моменты времени tʹ1 и tʹ2. Этим событиям соответствуют в
системе K моменты времени t1 и t2:
V
V
x
t 2 2 x
2
c
c
t1
; t2
2
2
2
2
1 V c
1 V c
t1
t2 t1
t2 t1
2
1 V c
2
.
t 2 t1 t ; t2 t1
2
V
t 1 2
c

15. Общефизический принцип относительности

Принцип относительности в трактовке Эйнштейна:
“Законы природы, по которым изменяются состояния
физических систем, не зависят от того, к какой из
инерциальных систем отсчёта относятся эти
изменения”.
В релятивистской механике импульс частицы:
p
mV
где для сохранения классической
1 V 2 c 2формулы
вводят понятие релятивистской массы :
p mV
- масса покоя
(при V= 0)
m
m рел
2
1 V c
2
; m

16.

Релятивистская энергия частицы
в отсутствие действия внешних
E
физических полей:
Связь между импульсом и энергией :
- формула Эйнштейна
E 2- энергия
E02 покоя
p 2c 2
частицы ( V= 0)
2
E0 mc энергия частицы
Кинетическая
K определяется выражением:
В области малых скоростей, где
кинетическая энергия:2
2 2
и
mc 2
1 V 2 c2
,
K E E0 E0 p c E0
V c
pc E 0
p 2c 2
p2
mV 2
K
2 E0
2m
2
.

17. РЕЛЯТИВИСТСКОЕ УРАВНЕНИЕ ДВИЖЕНИЯ

В специальной теории относительности уравнение
движения имеет тот же
вид, что и в механике
Ньютона: dp dt F , но:
p
d
mV
F
dt 1 V 2 c 2
1 V 2 c2
mV
ma
2
1 V c
2
2
m V c V a
1 V
2
c
2 32
F .
VF
2
2 F
a 1 V c
V .
2
m mc

18. Принцип соответствия

Суть этого принципа в том, что любая новая
теория, претендующая на более глубокое описание
физической действительности и на более широкую
область применимости, чем старая теория, должна
включать в себя эту старую теорию как предельный
случай. В полном согласии с принципом
соответствия преобразования
Лоренца переходят в преобразования Галилея, а релятивистский
закон динамики переходит в
классический закон Ньютона.

19. Неинерциальные системы отсчёта

Для описания механического движения можно также
использовать неинерциальные системы отсчета (НСО),
построенные на телах, которые движутся ускоренно.
Нерелятивистский второй закон Ньютона в НСО имеет
вид:
maотнускорение
Fинер. измеряемое в
- относительное
. F частицы,
где
НСО,aотн. - обычная сила взаимодействия
данной частицы с
другими частицами или внешними
физическими полями и
F
- сила инерции. Силы инерции обусловлены не
взаимодействием тел, а свойствами самих неинерциальных
отсчета.
систем
Fинер.

20.

Силы инерции неинвариантны относительно
перехода из одной системы отсчета в другую.
Они
не подчиняются закону действия и противодействия.
Движения тела под действием сил инерции аналогично
движению во внешнем силовом поле.
Силы инерции всегда являются внешними по
отношению
к
любому
движению
системы
материальных тел.
Допустим, что НСО движется поступательно с
ускорением относительно некоторой ИСО. В этом
случае сила инерции (поступательная сила инерции) в
уравнении
a
принимает вид:
Fинер. ma

21.

Ускорение a , с которым движется НСО, обычно
называется
переносным ускорением и обозначается
как a пер.. Ускорение частицы, измеряемое в ИСО,
называется
абсолютным ускорением и обозначается
как a абс. . Все три перечисленные выше ускорения
связаны простым соотношением:
a абс. a пер. aотн.
Уравнение относительного движения частицы:
maотн. F maпер.

22. Центробежная сила инерции

Если НСО и рассматриваемая частица вращаются с
одинаковой постоянной угловой скоростью ω вокруг оси Z
неподвижной ИСО, то на частицу действует центробежная
сила инерции
Fц .б . ma пер.
2
a пер. r
- радиус-вектор час в НСО, лежащий в плоскости, перпендикуляр- ной
тицы
r R
оси вращения.
2
апер.
V
2
2
an
R; Fцб mω R.
R

23.

R RЗ cos φ
где φ – широта
местности
2
2
Fцб mω R mω RЗ cos φ,
Сила тяжести есть результат сложения
Fg и Fцб P mg Fg Fцб
g (а значит и mg) зависят от широты местности
g = 9,80665 м/с2 – ускорение свободного
падения тела. Направлено g к центру только на
полюсе и на экваторе.

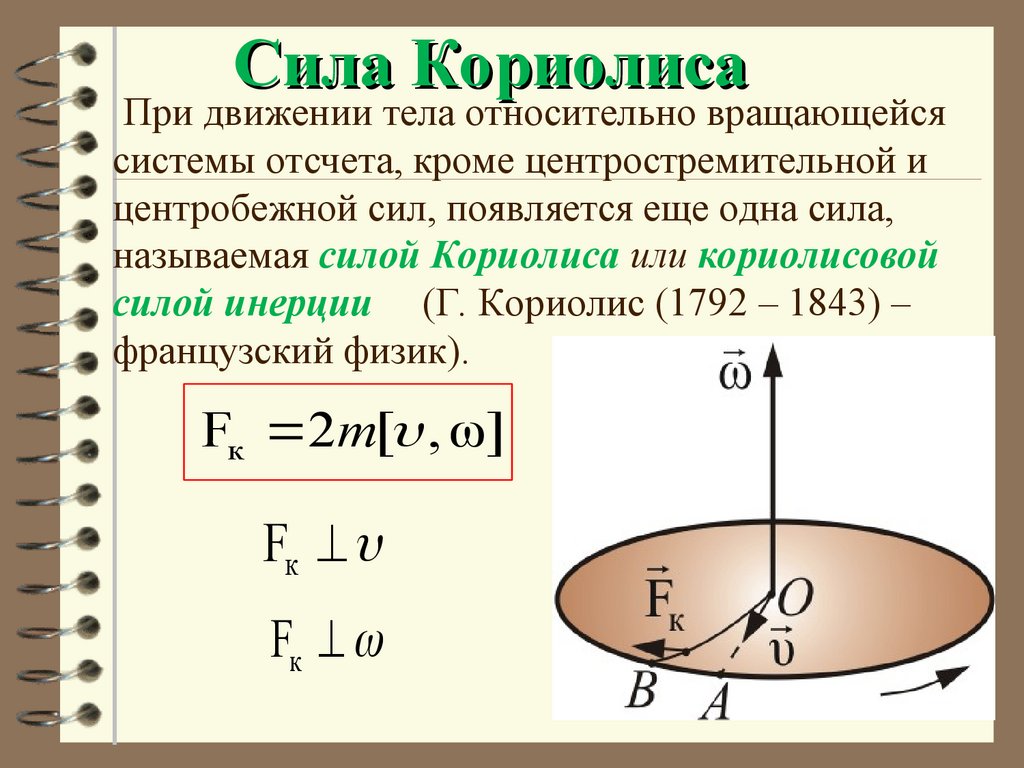
24. Сила Кориолиса

При движении тела относительно вращающейся
системы отсчета, кроме центростремительной и
центробежной сил, появляется еще одна сила,
называемая силой Кориолиса или кориолисовой
силой инерции (Г. Кориолис (1792 – 1843) –
французский физик).
Fк 2m[ , ω]
Fк
Fк

25.

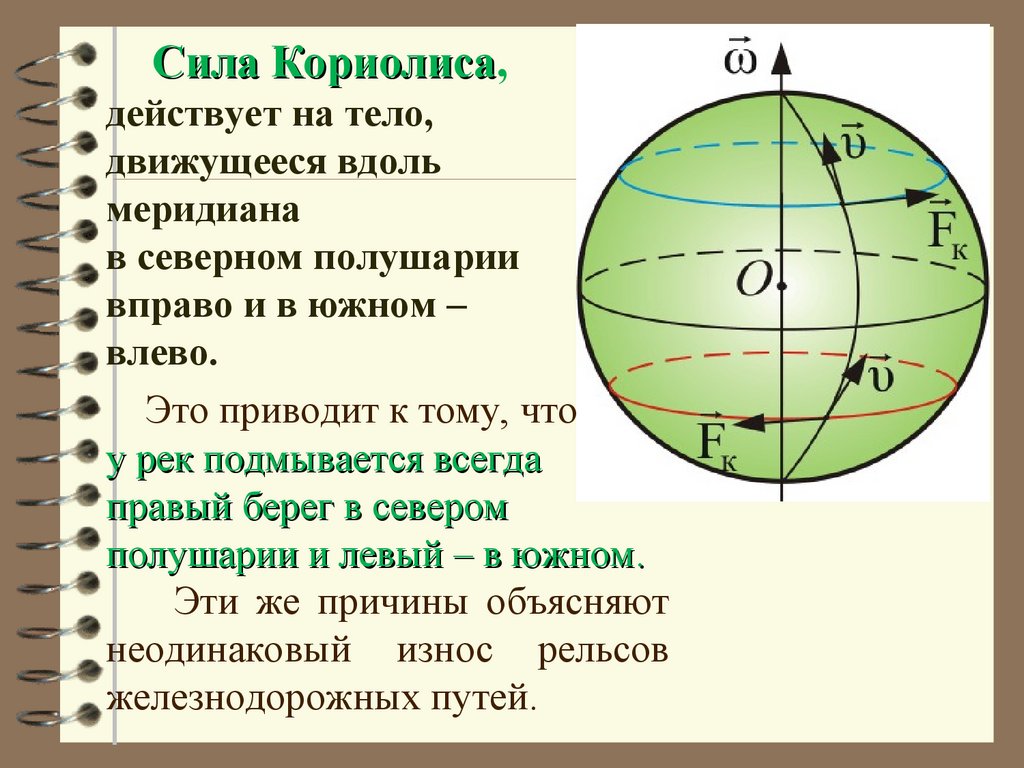
Сила Кориолиса,
Кориолиса
действует на тело,
движущееся вдоль
меридиана
в северном полушарии
вправо и в южном –
влево.
Это приводит к тому, что
у рек подмывается всегда
правый берег в севером
полушарии и левый – в южном.
Эти же причины объясняют
неодинаковый износ рельсов
железнодорожных путей.

26.

Силы Кориолиса проявляются и при качаниях маятника (маятник Фуко).
Фуко Плоскость качаний маятника
вследствие вращения Земли поворачивается, и
проекция траектории маятника на поверхность
Земли имеет вид розетки. Для простоты
предположим,
что маятник
расположен
на полюсе.

27.

Колебания маятника Фуко зависит от
того, как они были возбуждены. Если
маятник отклонить на максимальный
угол, а затем отпустить его без
начальной скорости , то маятник будет
колебаться, как изображено на верхней
анимации. Скорость движения
маятника в положении максимального
отклонения будет равна нулю
Несколько иной характер траектории
получится, если маятник приводится в
движение коротким толчком из
положения равновесия. Этому случаю
соответствует нижняя анимация.
Скорость маятника в положении
максимального отклонения
соответствует скорости вращения
Земли на широте наблюдения.

28.

С учетом всех сил инерции, уравнение Ньютона
для неинерциальной системы отсчета примет вид:
maотн. F Fин Fцб Fк ,
Fин– сила инерции, обусловленная поступательным
неинерциальной системы отсчета;
движением
Fцб Fк – две силы инерции, обусловленные
вращательным движением системы отсчета;
Fин ma , Fк 2m[ υ, ω],
Fцб man .

29.

Релятивистская теория тяготения
(общая теория относительности)
Теория тяготения Ньютона неприменима для описания
движения частиц вблизи массивных тел (в частности, для
описания траектории движения света в поле тяготения).
Неприменима теория тяготения Ньютона и для описания
переменных полей тяготения, создаваемых движущимися
телами.
Обобщение теории тяготения на основе специальной
теории относительности было сделано А. Эйнштейном в
1908 – 1916 гг. Эта теория была названа им общей
теорией относительности (ОТО).
Потенциальная энергия тела массы m в поле тяготения
равна:
где φ – потенциал поля
тяготения.
U m ,

30.

Если величина U мала по сравнению с
2
2
энергией тела mc т.е. если (φ / c ) 1
и тело движется со скоростью, много
меньшей скорости света ( c ) то мы
имеем
дело
с
классическим
гравитационным полем для которого
справедлив закон всемирного тяготения
Ньютона.
В полях тяготения обычных небесных тел
это условие выполняется:
2
6
на поверхности Солнца φ / c 4 10 ,
3
на поверхности белых карликов, 10 .

31.

Теория
тяготения
Ньютона
предполагает мгновенное распространение
полей тяготения, что не согласуется с
принципами
специальной
теории
относительности, основанной на том
экспериментальном факте, что любое
взаимодействие
распространяется
со
скоростью, меньшей или равной скорости
света.
Поэтому
теорию
тяготения
Ньютона нельзя применять к сильным
полям тяготения, разгоняющим частицы
до скорости, близкой к скорости света:
2
(φ / c 1)

32.

В ОТО описываются сильные
2
гравитационные
поля (φ / c 1)
и движение в них с большими
скоростями ( c )
В ОТО учитывается воздействие
материи на свойства пространства и
времени (искривление
пространства массивным телом ), а эти измененные свойства
пространства –времени
влияют на сам характер
физических процессов.

33. Принцип эквивалентности сил инерции и сил тяготения

Важнейшей особенностью полей тяготения
является то, что тяготение совершенно одинаково
действует на разные тела, сообщая им одинаковые
ускорения, независимо от свойств тел.
Между силами инерции,
инерции пропорциональными
инертной массе тела, и силой всемирного
тяготения,
тяготения пропорциональной гравитационной
массе, есть глубокое сходство, основанное на
равенстве этих масс для любого тела
m m
g
in
с относительной погрешностью
10-12.

34.

Тождественность инерциальной и гравитационной
масс mg
, является
следствием эквивалентности
min
сил инерции и сил тяготения.
тяготения
Этот факт называется принципом эквивалентности
Эйнштейна.
Эйнштейна Согласно этому принципу, все
физические процессы в истинном поле тяготения
и в ускоренной системе отсчета, в отсутствии
тяготения, протекают одинаковым образом. Это
фундаментальный закон природы. В отношении
механического движения в достаточно малой
области, где , переход в НСО, движущуюся с
постоянным ускорением , позволяет компенсировать
силу всемирного тяготения.
g a

35.

Принцип эквивалентности был использован
А. Эйнштейном при создании релятивистской
теории
гравитации
(общей
теории
относительности) в 1915 – 1916 гг., в основу
которой были положены два постулата:
1) все физические процессы в поле тяготения и в
НСО в достаточно малой пространственновременной области, где g const , протекают по
одинаковым законам ( принцип эквивалентности
сил инерции и сил гравитации);
2) максимальная скорость распространения любых
физических
взаимодействий,
включая
гравитационные, равна скорости света в вакууме.

36.

Ярчайшим доказательством равенства сил
инерции и гравитации является состояние
невесомости космонавтов в космическом корабле
(падают под действием гравитационных сил и
отлетают под действием центробежных сил
инерции). Принцип
эквивалентности –
основополагающий в ОТО Эйнштейна.

37.

СТО оперирует плоским пространством-временем,
пространством-временем
а ОТО – искривленным.
искривленным
Любая масса, искривляет пространство-время,
другая масса, попадая в область искривления,
испытывает силу притяжения.
Замедление времени в гравитационных полях.
Общая теория относительности предсказывает
замедление хода часов в гравитационных полях.
С точки зрения неподвижного наблюдателя
промежутки времени dt в неподвижной и dt0 в
подвижной системах отсчета связаны соотношением:
φ ( dt> dt0 )
dt dt0 1 2
c

38. Чёрные дыры

Уже есть достаточно веские доказательства
существования чёрных дыр.
дыр Основная трудность
состоит в том, что они поглощают все и почти ничего
не излучают. Поэтому об их существовании можно
судить по косвенным данным: поглощению вещества
и испусканию в этом процессе излучения.
Пространство внутри чёрных дыр сворачивается,
время практически останавливается. Можно
оценить размеры rg и массу М космического объекта,
способного стать черной дырой.
Если
то свет не сможет покинуть
данный космический объект.
2M
r G
c
g
2

39.

А

40.

ОТО предполагает наличие во Вселенной черных дыр космических объектов, поглощающих все частицы, в том
числе фотоны, подходящие к их поверхности. Они образуются
в результате взрыва гигантских звезд массой более 3 масс
Солнца. Вблизи черной дыры газ сильно разогревается
и становится
источником
высокоэнергичного электромагнитного
излучения в
рентгеновском и гамма - диапазоне.

41.

Согласно современным экспериментальным данным
лишь 5% всей массы Вселенной составляет известное
нам вещество.
вещество При этом примерно для 30% массы
Вселенной справедлив закон гравитационного
притяжения,
притяжения а для ~70% (так называемой “темной
энергии”) наблюдается гравитационное отталкивание.
отталкивание
Благодаря гравитационному отталкиванию материи в
виде “темной энергии” наша
Вселенная расширяется
ускоренно.
ускоренно Роль антигравитации в динамике Вселенной со временем будет
только возрастать, поэтому именно неизвестная нам
“темная энергия” определяет будущее Вселенной.

42. Система материальных точек

Рассмотрим систему, состоящую из n материальных
точек с заданными массами m
, где
- номер
i 1,2,...,
n
i
частицы. Состояние системы материальных точек
задаётся путём определения состояния всех
материальных точек, входящих в данную систему:
ri t , Vi t
Центром масс (или центром инерции)
инерции системы
материальных точек называется воображаемая точка С,
положение которой характеризует распределение массы
этой системы.
n
n
Ее радиус-вектор равен:
mi ri
rc i n1
mi
i 1
mi ri
i 1
m

43. Центр масс ( инерции )

Воображаемую точку С с радиус-вектором
1 n
rc mi ri
m i 1
где i - номер точки,
n - количество точек,
mi - масса i-ой точки и
m - масса всей системы
точек
называют центром масс
системы материальных
точек
Z
С
rc
O
X
Y

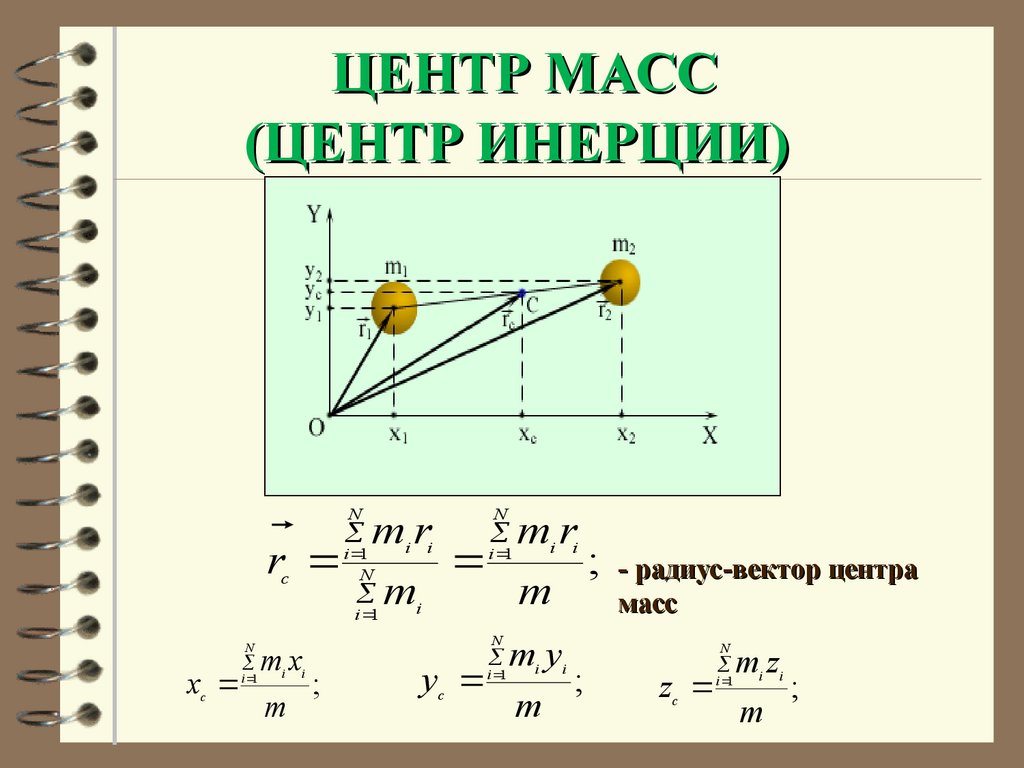
44. ЦЕНТР МАСС (ЦЕНТР ИНЕРЦИИ)

mr
i i
i 1
N
rc
N
i 1
mi
xc
mi xi
i 1
m
m
;
- радиус-вектор центра
масс
N
N
mr
i i
i 1
N
;
yc
mi yi
i 1
m
N
;
zc
i 1
mi zi
m
;

45. Аддитивность массы в нерелятивистской механике.

Полная масса системы материальных точек:
n
m mi
i 1
в области малых скоростей cнаходится
путём сложения масс всех частиц систем (здесь
используется аддитивность массы в
нерелятивистской механики). В релятивистской механике масса системы частиц зависит от
энергии взаимодействия между частицами,
поэтому последняя формула не справедлива.

46. Скорость центра масс системы материальных точек

Взяв производную rc по времени, получим
скорость центра масс:
n
drc 1
dri 1 n
c mi
mi υi
dt m i 1
dt m i 1
dri
где
i - скорость i-ой материальной
dt
точки системы

47. Полный импульс системы материальных точек (частиц)

В нерелятивистской механике полный импульс системы
материальных точек равен сумме импульсов всех частиц
системы:
n
p pi
i 1 i–ой частицы.
- импульс
mi υi n
, где
n
m ц.м.
i 1 mi
mi υi mυc - скорость
то импульс системы
по формуле:
i 1 частиц можно определить
υ
где
pi
Так как
c
p mυc

48.

n
pc m c mi i
- импульс центра масс
i 1
Импульс системы материальных точек
(импульс центра масс) равен произведению
массы системы на скорость ее центра масс.
Таким образом связь импульса pc со
скоростью υc такая же, как для
материальной точки с массой m
(масса
системы).

49.

50. Основное уравнение динамики поступательного движения произвольной системы частиц

Тела, не входящие в состав рассматриваемой
системы, называют внешними телами,
телами а силы,
действующие на систему со стороны этих тел –
внешними силами.
силами Силы взаимодействия
между телами внутри системы, называют
внутренними силами.
силами
Результирующая всех внутренних сил
действующих на i-ое тело:
внутр. n
Fi
Fik Fi1 Fi 2 ... Fin ,
где k
себя.
i
k i
– т.к. i-ая точка не может действовать сама на

51.

внеш.
Обозначим Fi
– результирующая всех
внешних сил приложенных к i-ой точке системы.
По второму закону Ньютона можно записать
систему уравнений:
внеш.
d
m1υ1 F1 F12 F13 ... F1n ,
dt
внеш.
d
m2υ2 F2 F21 F23 ... F2n ,
dt
...............................,
внеш.
d
mnυn Fn Fn1 ... Fn,n 1.
dt

52.

Сложим
эти
уравнения и сгруппируем попарно
силы Fik и Fki:
n
n
d
внеш.
dt mi υi Fi F12 F21 ... Fn 1,n Fn,n 1 .
i 1
i 1
По третьему закону Ньютона Fik Fki ,
поэтому все выражения в скобках в правой части
уравнения равны нулю. Тогда получаем:
d
dp
внеш.
mi υi Fi
.
dt
i 1 dt
i 1
n
n
n
внеш.
F Fi
–
Назовем
внешних сил,
i 1
тогда:
главным вектором всех
dp
F.
dt

53.

dp
F
dtвнешних
Скорость изменения импульса системы
равна главному вектору всех
сил,
действующих на эту систему.
Это уравнение называют основным
уравнением динамики поступательного
движения системы тел. Так как импульс
системы p mυ
то:
c
d
mυc F
dt
Тогда можно записать основное уравнение
динамики поступательного движения системы
тел в виде:
mac F
где
ac
– ускорение центра

54.

Центр механической системы движется как
материальная точка, масса которой равна массе
всей системы, и на которую действует сила, равная
главному вектору внешних сил, приложенных к
системе:
m
a
F
c
На основании третьего закона Ньютона,
Ньютона силы,
действующие на тела системы со стороны других тел
системы (внутренние силы), взаимно компенсируют
друг друга. Остаются только внешние силы.
В общем случае движение тела можно
рассматривать
как
сумму
двух
движений:
поступательного со скоростью
и
вращательного вокруг центра масс.
масс
υ υc

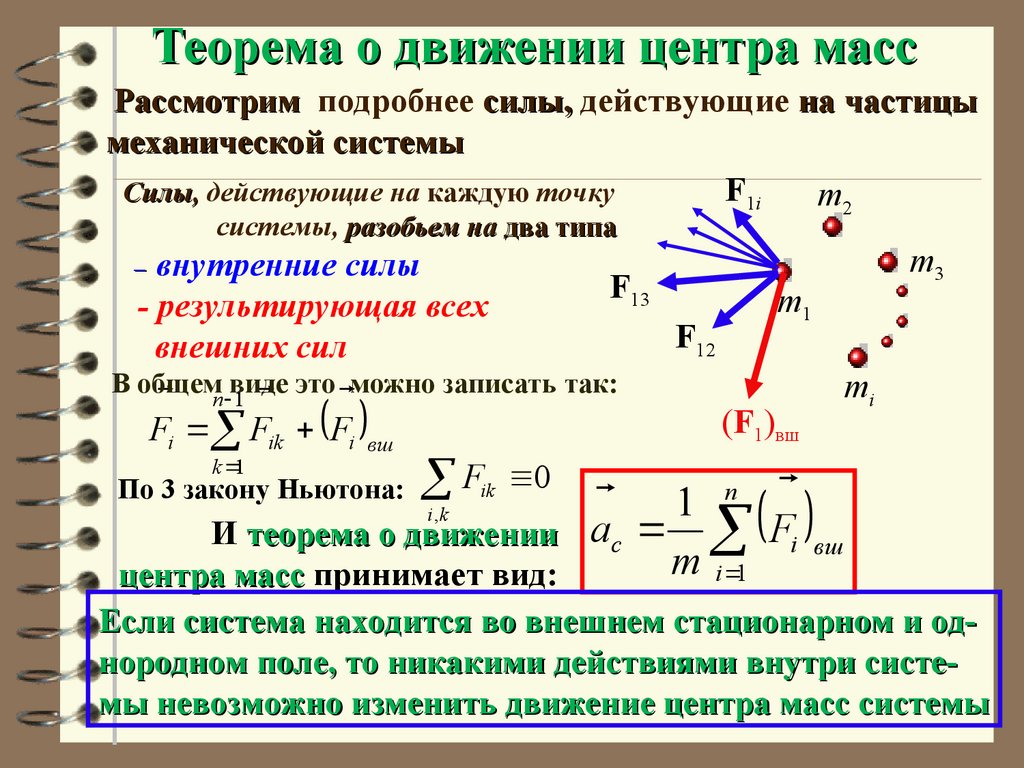
55. Теорема о движении центра масс

Рассмотрим подробнее силы, действующие на частицы
механической системы
F1i
Силы, действующие на каждую точку
m2
системы, разобьем на два типа
внутренние силы
- результирующая всех
внешних сил
–
F13
В общемn виде
это можно записать так:
1
Fi Fik Fi
вш
F12
m3
m1
(F1)вш
mi
По 3 закону Ньютона: Fik 0
n
1
i ,k
Fi вш
И теорема о движении ac
m i 1
центра масс принимает вид:
Если система находится во внешнем стационарном и однородном поле, то никакими действиями внутри системы невозможно изменить движение центра масс системы
k 1

56. Закон сохранения импульса

Механическая система называется замкнутой
(или изолированной), если на неё не действуют
внешние силы, т.е. она
не
взаимодействует с
n
внеш.
0.
внешними телами или F Fi
i 1
Строго говоря, каждая реальная система тел
всегда не замкнута, т.к. подвержена, как минимум
воздействию гравитационных сил. Однако если
внутренние силы гораздо больше внешних, то
такую систему можно считать замкнутой
(например – Солнечная система).
Для замкнутой системы равнодействующий
вектор внешних сил тождественно равен нулю:
dp
F 0
dt

57.

отсюда
n
p mi υc const.
i 1
Это есть закон сохранения импульса:
импульса импульс
замкнутой системы не изменяется во времени.
Импульс системы тел может быть представлен в
виде произведения
массы тел на скорость
суммарной
центра инерции: p mυc , тогда
mυc const
При любых процессах, происходящих в замкнутых
(изолированных) системах, скорость центра масс
сохраняется неизменной.
Закон сохранения импульса является одним из
основных законов природы. Он был получен как следствие
законов Ньютона, но он справедлив и для микрочастиц и
для релятивистских скоростей, когда
c .

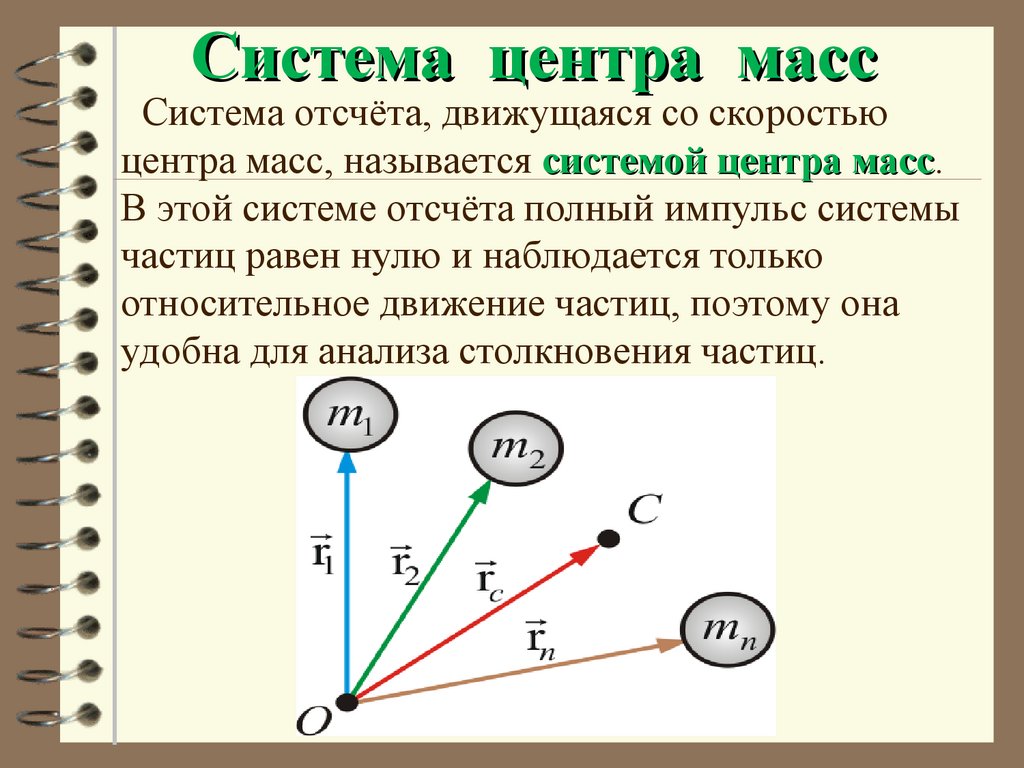
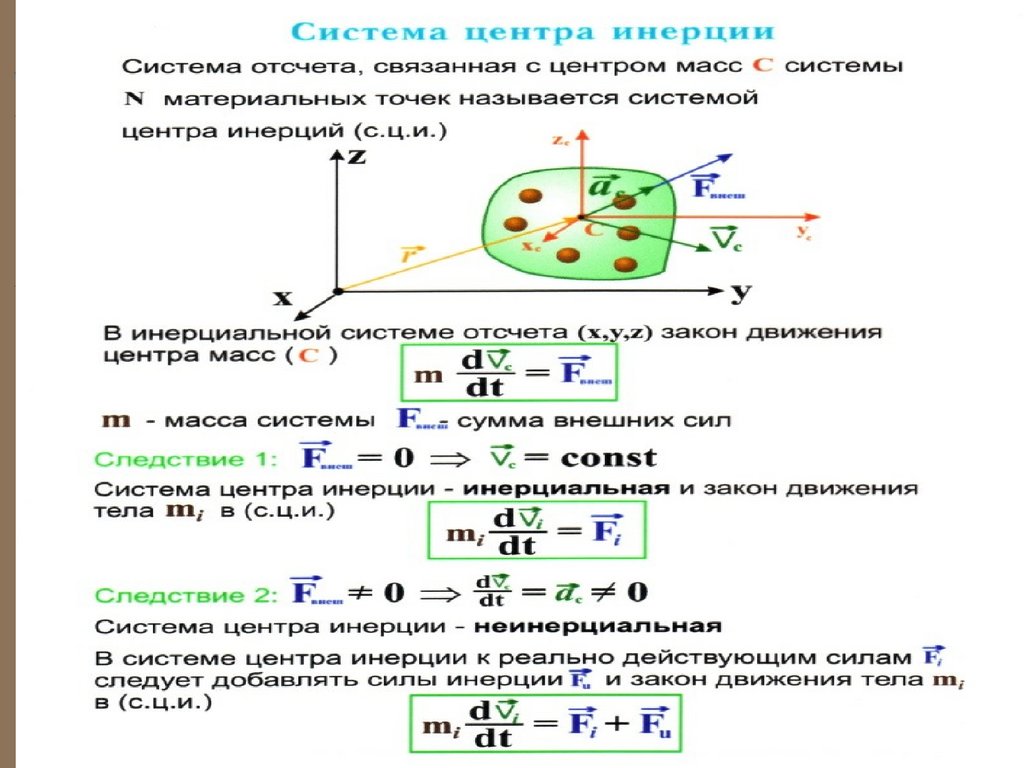
58. Система центра масс

Система отсчёта, движущаяся со скоростью
центра масс, называется системой центра масс.
масс
В этой системе отсчёта полный импульс системы
частиц равен нулю и наблюдается только
относительное движение частиц, поэтому она
удобна для анализа столкновения частиц.

59.

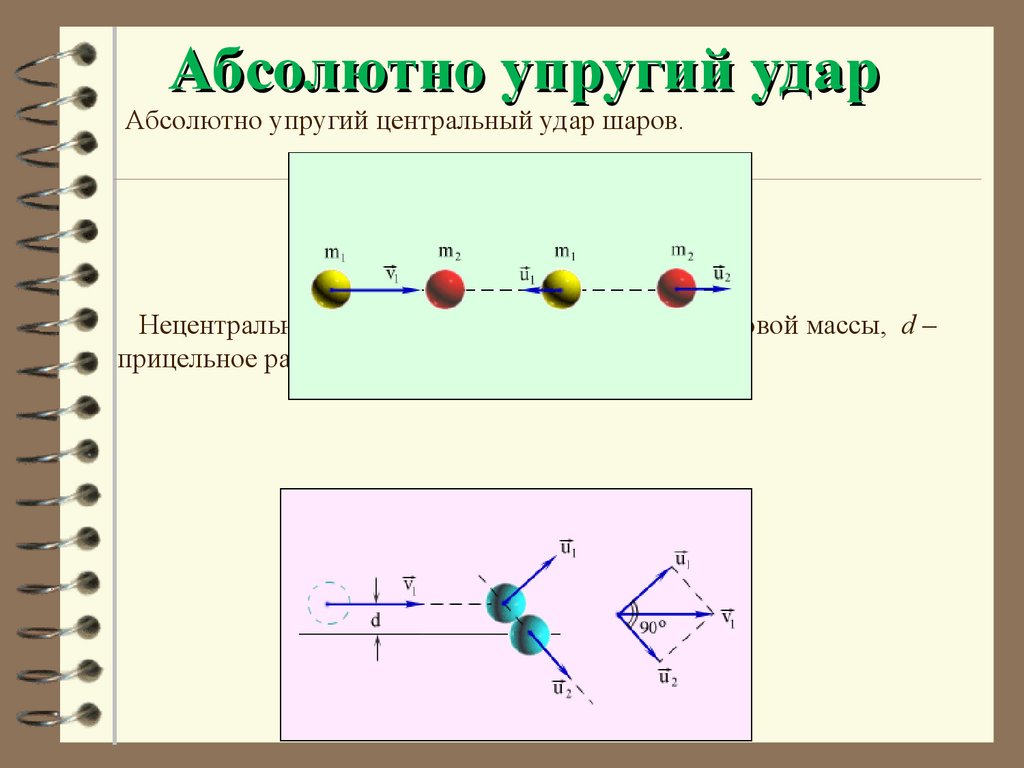
60. Абсолютно упругий удар

Абсолютно упругий центральный удар шаров.
Нецентральное упругое соударение шаров одинаковой массы, d –
прицельное расстояние.

61.

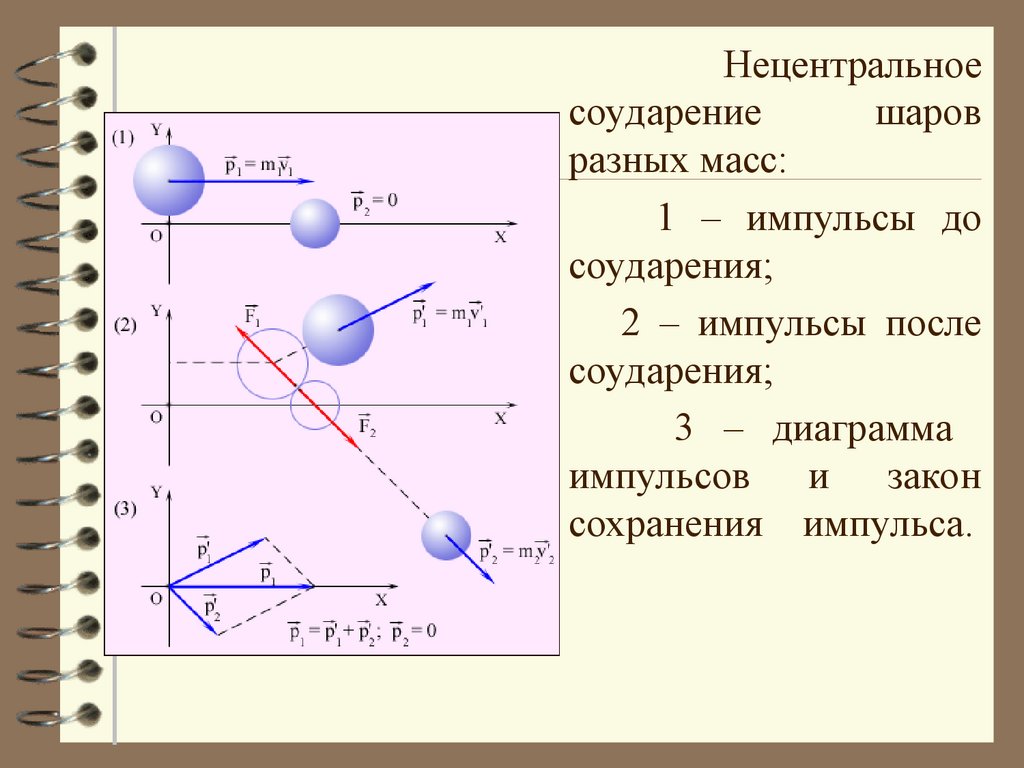
62.

Нецентральное
соударение
шаров
разных масс:
1 – импульсы до
соударения;
2 – импульсы после
соударения;
3 – диаграмма
импульсов и закон
сохранения импульса.

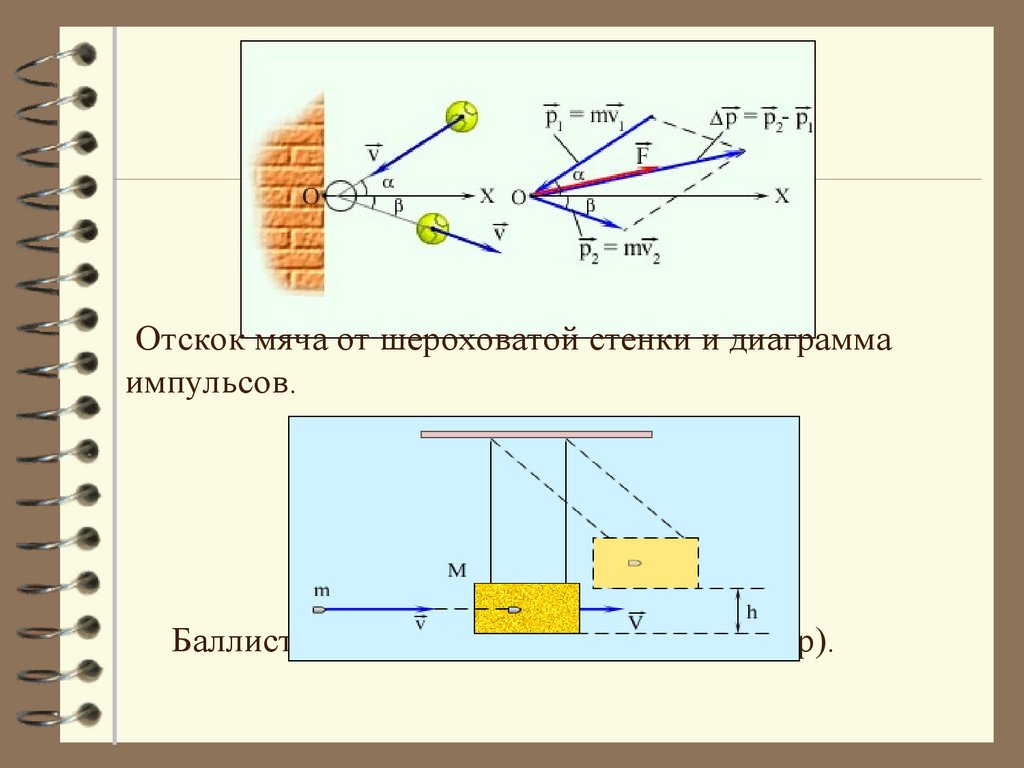
63.

Отскок мяча от шероховатой стенки и диаграмма
импульсов.
Баллистический маятник (неупругий удар).

64.

65.

При стрельбе из орудия возникает отдача – снаряд
движется вперед, а орудие – откатывается назад.
Снаряд и орудие – два взаимодействующих тела.
Скорость, которую приобретает орудие при отдаче,
зависит только от скорости снаряда и отношения масс.

66.

67. Реактивное движение

( движение тел с переменной массой)
Движение тела, возникающее вследствие
отделения от него части его массы с некоторой
скоростью, называют реактивным. Масса ракеты
уменьшается вследствие истечения газов,
образующихся при сгорании топлива.
Получим уравнение движения тела
переменной массы на примере движения ракеты.

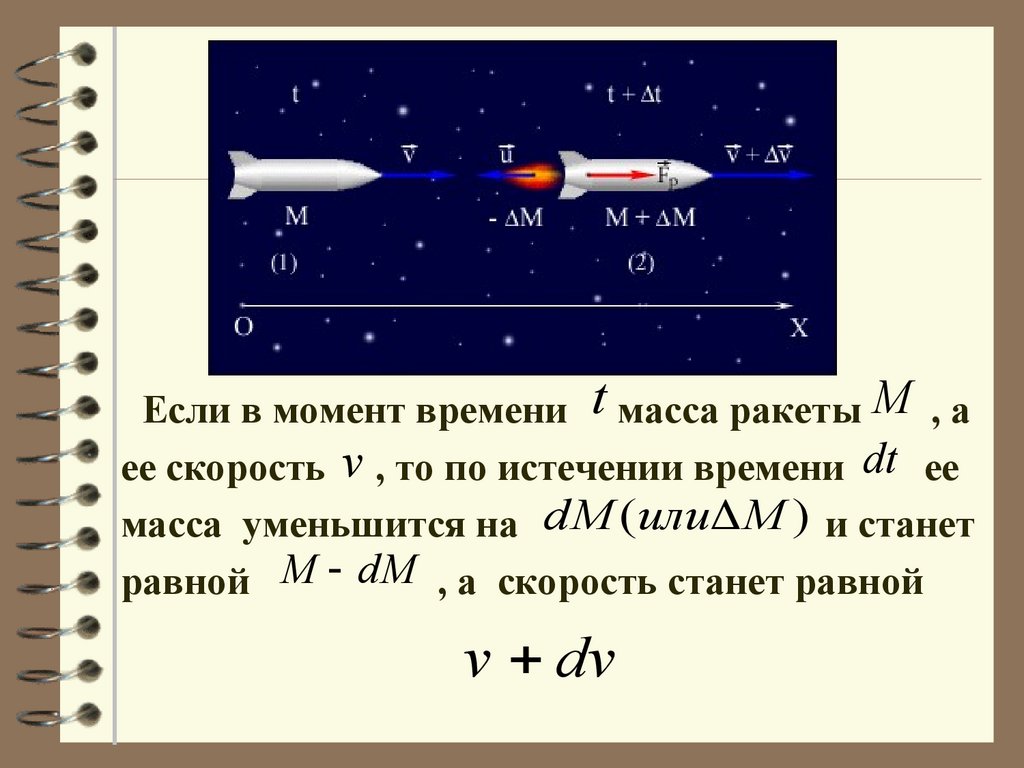
68.

Если в момент времени t масса ракеты M , а
ее скорость v , то по истечении времени dt ее
масса уменьшится на dM (или M ) и станет
равной M dM , а скорость станет равной
v dv

69.

Запишем изменение импульса за отрезок времени dt
dp ( M dM )(v dv ) dM (v u ) Mv
где u - скорость истечения газов относительно ракеты.
dp Mdv u dM
Тогда
(при этом пренебрегли слагаемым)
dMdv
Если на систему действуют
внешние силы, то
dp Fdt
, тогда
Fdt Mdv u dM
dM
dv
M
F u
dt
dt
или

70.

Второе слагаемое в правой
части называют
dM
реактивной силой: Fр u
dt
Если u противоположен v по направлению,
то
ракета ускоряется, а если совпадает с
v
, то
тормозится.
Получено уравнение движения тела с
переменной массы (уравнение Мещерского):
Мещерского
Ma F Fр
где реактивная сила
dM
Fр u
dt

71.

ИВАН ВСЕВОЛОДОВИЧ МЕЩЕРСКИЙ
(1859—1935)
И. В. Мещерский является основоположником
механики тел переменной массы.

72.

Применим уравнение к движению ракеты, на которую
не действуют
силы
никакие внешние силы.
Полагая
F 0 и считая, что скорость
выбрасываемых
газов относительно ракеты постоянна (ракета движется
M o момент скорость ракеты
прямолинейно) и в начальный
равна нулю,
dvа масса равна
dM
M
u
dt
dt
, получим:
dM
Mdv
udM
; dvХ : u
В проекции
на ось
M
dM
v u
ulnM C
M

73.

Значение постоянной интегрирования C определим
из начальных условий. Если в начальный момент
времени скорость ракеты равна нулю, а ее
Mo
стартовая
массаC u
, то
ln M , следовательно,
o
Mo
v u ln
M
- формула Циолковского
M , тем больше
должна быть стартовая масса ракеты M o .
Чем больше конечная масса ракеты
Чем больше скорость истечения газов , тем больше
u
может быть конечная масса при данной стартовой
массе
ракеты.

74.

Константин
Эдуардович
Циолковский
(1857-1835)
К.Э.Циолковский
разработал принципы
реактивного движения,
ученый и
изобретатель,
основоположник
современной
космонавтики и
ракетной техники.

75. Ракеты

76.

Реактивный самолёт-амфибия

77. Реактивный катер

78. Реактивная система залпового огня “Смерч”

79. Реактивный ранец

80.

ЛЕКЦИЯ ЗАКОНЧЕНА!