Угол между плоскостями. Задание 13

1.

2.

Повторение:
Двугранный угол, образованный полуплоскостями
измеряется величиной его линейного угла, получаемого при
пересечении двугранного угла плоскостью,
перпендикулярной его ребру.
S
А
N
F
В
М
X
Двугранный угол АВNМ, где ВN – ребро, точки А и М лежат в
гранях двугранного угла
Угол SFX – линейный угол двугранного угла

3.

Повторение:
Алгоритм построения линейного угла.
D
Угол РОК – линейный угол
двугранного угла РDEК.
Р
О
К
E
Плоскость линейного угла (РОК) DE.

4.

Повторение:
Угол между пересекающимися плоскостями
можно вычислить:
1) Как угол между прямыми, лежащими в этих плоскостях и
перпендикулярными к линии их пересечения;
2) Как угол треугольника, если удается включить линейный
угол в некоторый треугольник;
3) Используя координатно –векторный метод;
4) Используя ключевые задачи;

5.

Устно:
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
АС ВМ
перпендикуляр
В
К
TTП
АС NМ
А
M
N проекция
С
Угол ВMN – линейный угол двугранного угла ВАСК

6.

Устно:
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
АС NС
В
перпендикуляр
АС ВС
TTП
А
С
К
N
Угол ВСN – линейный угол двугранного угла ВАСК

7.

Устно:
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
АС NS
В
перпендикуляр
АС ВS
TTП
А
С
S
К
N
Угол ВSN – линейный угол двугранного угла ВАСК

8.

Устно:
Найдите тангенс угла между диагональю куба и
плоскостью одной из его граней.
D1
перпендикуляр
А1
А
С1
Подсказка
В1
М
D
В
перпендикуляр
С
А
Н
проекция
Углом между прямой и плоскостью, пересекающей
эту прямую и не перпендикулярной к ней,
называется угол между прямой и ее проекцией на

9.

Устно:
Дан куб. Найдите следующие двугранные углы:
АВВ1С; б) АDD1B; в) А1ВВ1К,
где К середина ребра А1Д1
D1
С1
K
А1
В1
D
А
С
В

10.

Устно:
В кубе ABCДA1B1C1Д1 , Докажите, что плоскости
АВС1 и А1В1D перпендикулярны .
D1
А1
С1
В1
D
А
С
В

11.

№1
В единичном кубе АВСДА1В1С1Д1 найдите
тангенс угла между плоскостями АДД1 и
ВДС1 .
D1
С1 Задача окажется значительно
проще, если расположить куб
иначе!!!
1
А1
В1
1
1
D
А
С
1
В

12.

№1
В единичном кубе АВСДА1В1С1Д1 найдите
тангенс угла между плоскостями АДД1 и
ВДС1 .
1) Плоскость AДД1 параллельна
А1 плоскости ВСС1, искомый угол
равен углом между плоскостями
ВСС1 и ВДС1 .
ВСС1 ВДС1 ВС
ОС ВС
ДОС
линейный угол
ОД ВС
А
D
1
D1
В
В1
2
2
С
1
О
1
С1
Ответ: 2

13.

Критерии оценивания выполнения задания С2
баллы
Критерии оценивания
2
Правильный ход решения. Верно построен или описан
искомый угол. Получен верный ответ
1
1) Правильный ход решения. Получен верный ответ,
но имеется ошибка в построении и описании искомого
угла, не повлиявшая на ход решения
2) Правильный ход решения. Верно построен и описан
искомый угол, но имеется ошибка в одном из
вычислений, допущенная из-за невнимательности, в
результате чего получен неверный ответ
0
1) Ход решения правильный, но оно не доведено до
конца, или решение отсутствует. Нет ответа
2)
Ход
решения
правильный,
но
имеются
существенные ошибки в вычислениях, приведшие к
неправильному ответу
3) Неправильный ход решения, приведший к
неверному ответу

14.

№2
1
В единичном кубе АВСДА1В1С1Д1 точки Е, F –
середины ребер соответственно А1В1 и А1Д1.
Найдите тангенс угла между плоскостями
АЕF и ВСС1 .
D1
С1 1) Плоскость AДД1 параллельна
плоскости ВСС1, искомый угол
равен углом между плоскостями
АДД1 и АЕF .
АДД1 АЕF AF
ЕМ AF
АМЕ
линейный угол
АМ AF
F
Е
А1
М
В1
1
D
А
С
Е
Подсказка:
1
2
1
В
А
М
1
5
Ответ: 5
2

15.

В прямоугольном параллелепипеде АВСДА1В1С1Д1,
у которого АВ = 6, ВС = 6, СС1 = 4, найдите тангенс
угла между плоскостями АСД1 и А1В1С1.
№3
D1
6
С1 1) Плоскость AВС параллельна
плоскости А1В1С1, искомый
угол равен углом между
плоскостями АСД1 и А1В1С1 .
6
А1
В1
АВС АД1С АС
4
Д 1О АС
ДО АС
4
D
С
3 2
А
ДОД 1
линейный угол
6
О
6
В
Ответ: 8
3

16.

№4
Сторона основания правильной треугольной
призмы ABCA1B1C1 равна 2, а диагональ боковой
грани равна 5 . Найдите угол между
плоскостью A1BC и плоскостью основания призмы.
С1
А1
(ДЕМО 2011)
самостоятельно
В1
5
С
А
М 2
2
В
Ответ: 300

17.

№5
А1
В правильной треугольной призме
АВСА1В1С1 , все ребра которой равны 1,
найдите косинус угла между плоскостями
АСВ1 и ВА1С1.
С1
АСВ1 АВ1С ДЕ
1
3
1
В1М ДЕ
К
КМВ1
2
линейный угол
В1 МК ДЕ
7
4
7
4
1
М
Д
Е
С
А
1
В
Ответ: 17 1

18.

№6
В правильной четырехугольной пирамиде
SАВСД, все ребра которой равны 1. Найдите
косинус двугранного угла, образованного
гранями SВС и SCD.
S
Самостоятельно:
1
К
1
С
D
О
А
1
1
В
Ответ: –1
3

19.

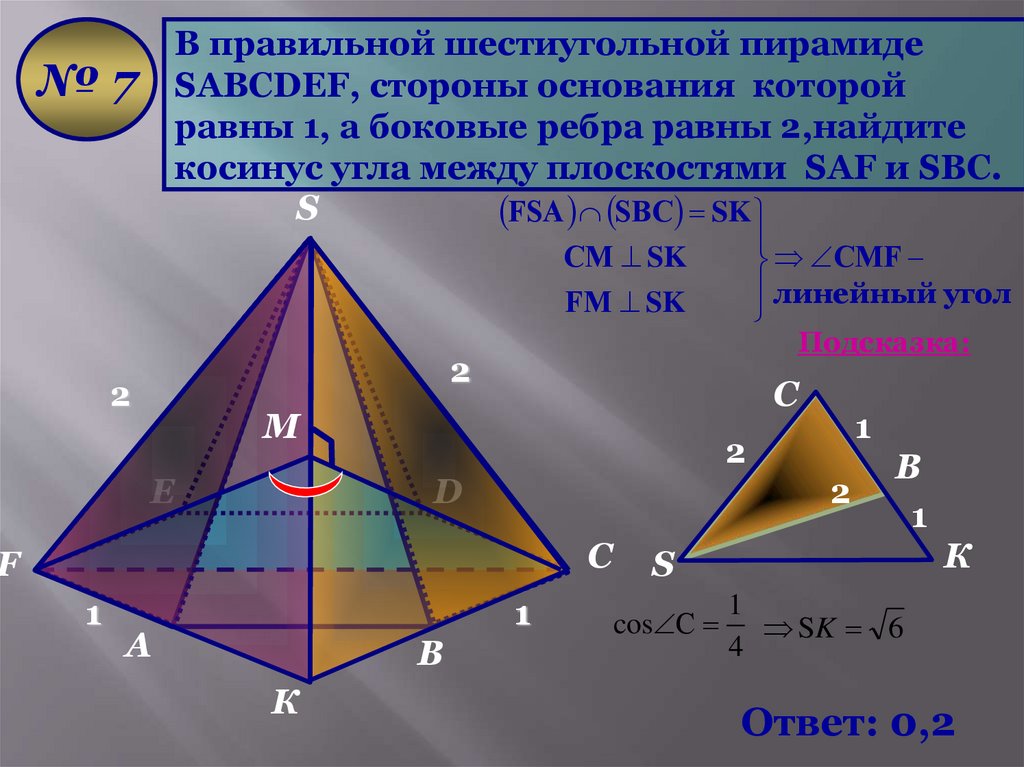
В правильной шестиугольной пирамиде
SАВСDЕF, стороны основания которой
равны 1, а боковые ребра равны 2,найдите
косинус угла между плоскостями SАF и SВС.
S
FSА SВС SK
№7
CМF
линейный угол
Подсказка:
CМ SK
FМ SK
2
2
С
М
Е
2
D
2
С
F
1
1
А
В
К
1
В
1
К
S
1
cos С SK 6
4
Ответ: 0,2

20.

В правильной шестиугольной призме A … F1,
все ребра которой равны 1, найдите
угол между плоскостями AВС и CА1Е1
№8
Е1
F1
D1
К
Самостоятельно:
С1
А1
В1
1
Е
F
D
С
М
А
1
В
1
2
Ответ: 3

21.

Литература
1. В.А. Смирнов ЕГЭ 2011. Математика.
Задача С2. Геометрия. Стереометрия. /
Под. редакцией А.Л. Семенова и И.В.
Ященко. – М.: МЦНМО, 2011.