1.14M

Category: $mathematics$ mathematics

Единый государственный экзамен. Математика - 2012. Задачи типа С2

1.

ЕДИНЫЙ
ГОСУДАРСТВЕННЫЙ
ЭКЗАМЕН
МАТЕМАТИКА - 2012
ЗАДАЧИ ТИПА С2

2.

Типы задач
Расстояние от точки до прямой
Расстояние от точки до плоскости
Расстояние между скрещивающимися
прямыми
Угол между прямыми
Угол между прямой и плоскостью
Угол между плоскостями

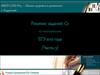
Повторение:
а
Н
Расстояние от точки до прямой, не
содержащей эту точку, есть длина
перпендикуляра, проведенного из
этой точки на прямую.
А
Расстояние от точки до прямой
можно вычислить:
1) Как длину отрезка перпендикуляра, если удается
включить этот отрезок в некоторый треугольник в качестве
одной из высот;
2) Используя координатно – векторный метод;

5.

Повторение:
А
М
Отрезок АН – перпендикуляр
Точка Н – основание
перпендикуляра
Отрезок АМ – наклонная
Точка М – основание наклонной
Отрезок МН – проекция наклонной
а
на прямую а
Н
Из всех расстояний от точки А до различных точек
прямой а наименьшим является длина перпендикуляра.

6.

№1
В единичном кубе АВСДА1В1С1Д1 найдите
расстояние от точки А до прямой ВД1.
1
D1
1) Построим плоскость AD1В,
проведем из точки А
перпендикуляр. АМ – искомое
расстояние.
С1
1
А1
В1
2
3
1
М
D
2) Найдем искомое расстояние
через вычисление площади
треугольника AD1В.
АА1 Д1 : АД1 1 1 2
С
d2 a 2 b2 c2
ВД1 12 12 12 3
А
S АВD1
1
1
ab
2
S АВD1
1
сhс
2
В SABD 1 3 AM 1 1 2
1
2
2
6
АМ
3
Ответ: 6
3

7.

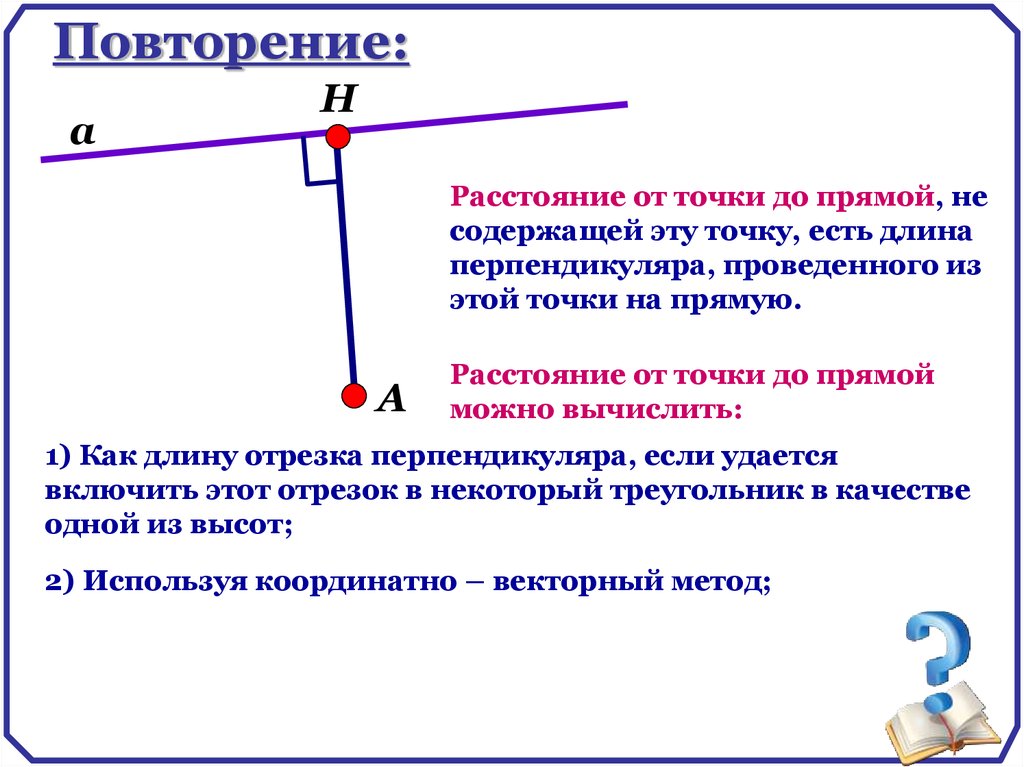
В единичном кубе АВСДА1В1С1Д1 найдите
расстояние от точки В до прямой ДА1.
№2
D1
А1
С1
А
Попробуем развернуть куб …
В1
D
С
В
Данный чертеж не является
наглядным для решения данной
задачи

8.

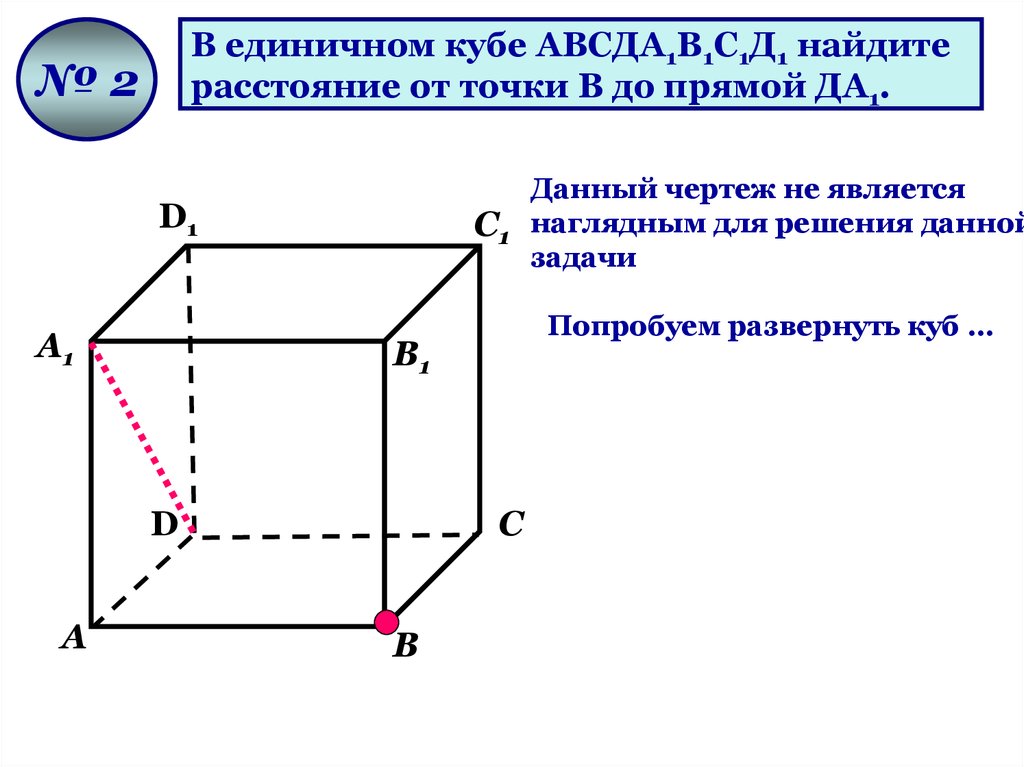
В единичном кубе АВСДА1В1С1Д1 найдите
расстояние от точки В до прямой ДА1.
№2
1) Построим плоскость DВA1,
проведем из точки В
ВМ – искомое
Вперпендикуляр.
1
расстояние.
1
В
1
Решить самостоятельно …..
С
С1
1
А
А1
1
М
D
1
D1
Ответ: 6
2

9.

№3
В правильной треугольной призме
АВСА1В1С1 , все ребра которой равны 1,
найдите расстояние от точки В до прямой АС1.
С1
В1
А1
Решить самостоятельно …..
1
М
1) Построим плоскость АВС1,
проведем из точки В
перпендикуляр. ВМ – искомое
расстояние.
1
С
1
А
1
1
В
Ответ: 14
4

10.

В правильной шестиугольной пирамиде
SАВСDЕF, стороны основания которой
равны 1, а боковые ребра равны 2,
найдите расстояние от точки S до прямой ВF.
№4
S
Подсказка:
а) FАВ = 1200
б) Рассмотреть
прямоугольный ∆АВМ
2
2
Е
F
1) Построим плоскость FSВ,
проведем из точки S
перпендикуляр. SМ – искомое
расстояние.
D
С
М
1
А
1
1
В
Ответ: 13
2

11.

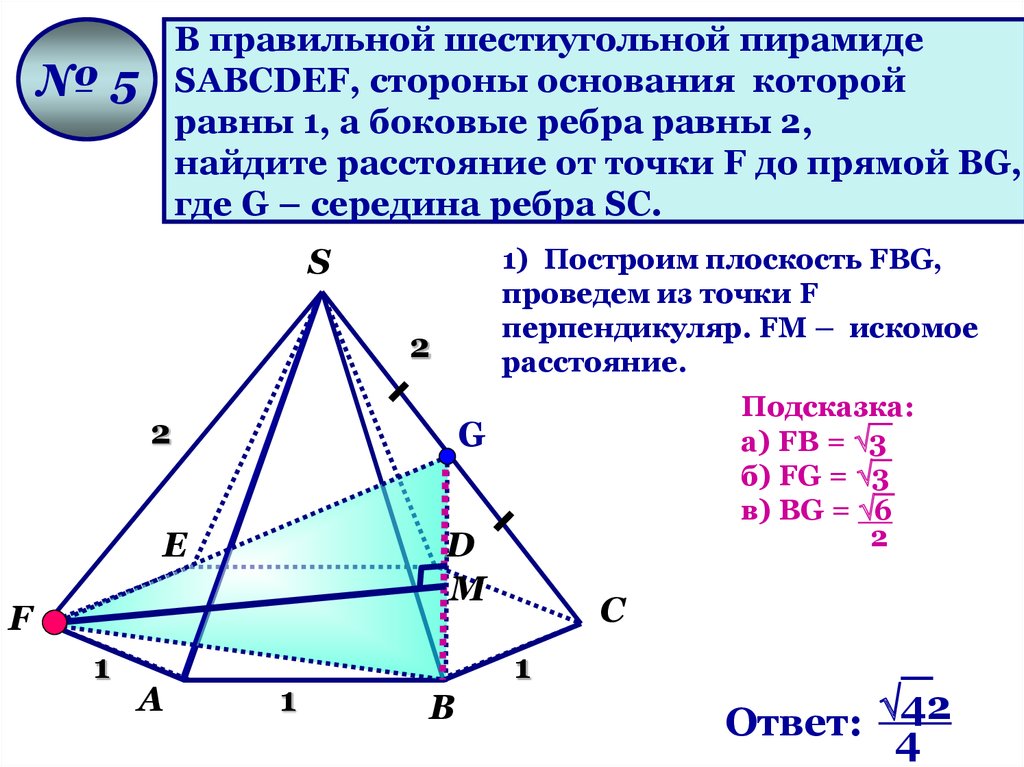
В правильной шестиугольной пирамиде
SАВСDЕF, стороны основания которой
равны 1, а боковые ребра равны 2,
найдите расстояние от точки F до прямой ВG,
где G – середина ребра SC.
№5
S
1) Построим плоскость FВG,
проведем из точки F
перпендикуляр. FМ – искомое
расстояние.
2
2
G
Е
D
М
F
1
А
Подсказка:
а) FВ = 3
б) FG = 3
в) ВG = 6
2
1
С
1
В
Ответ: 42
4

12.

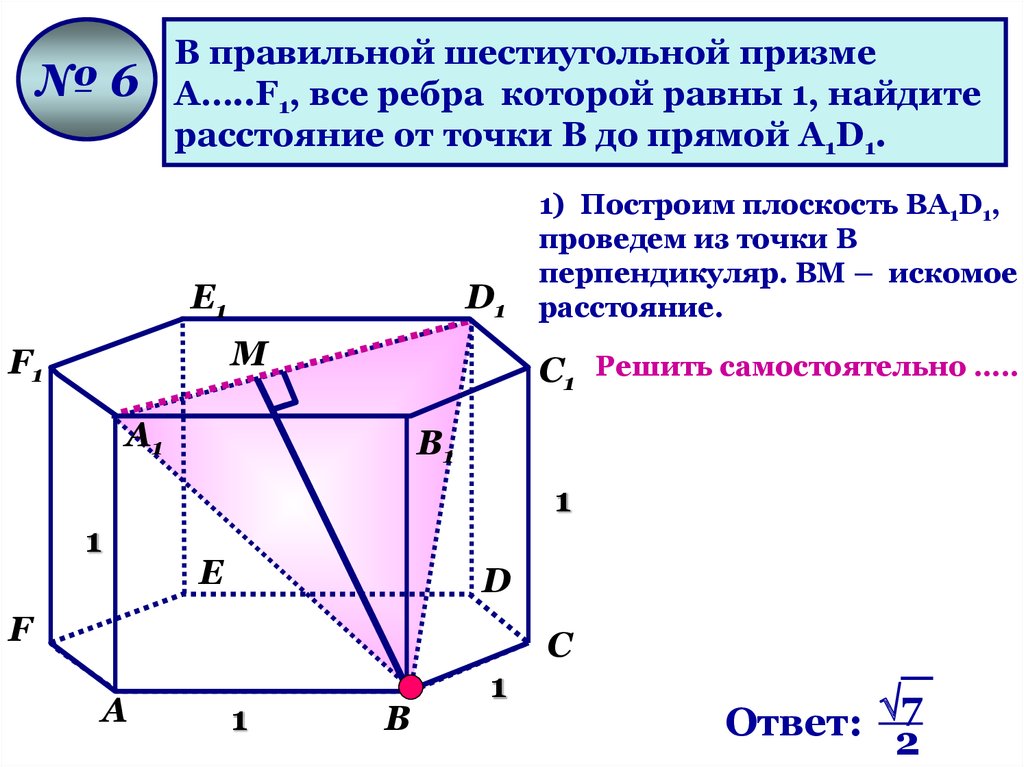
№6
В правильной шестиугольной призме
А…..F1, все ребра которой равны 1, найдите
расстояние от точки В до прямой А1D1.
Е1
D1
М
F1
1) Построим плоскость ВА1D1,
проведем из точки В
перпендикуляр. ВМ – искомое
расстояние.
С1 Решить самостоятельно …..
А1
В1
1
1
Е
D
F
С
А
1
В
1
Ответ: 7
2

13.

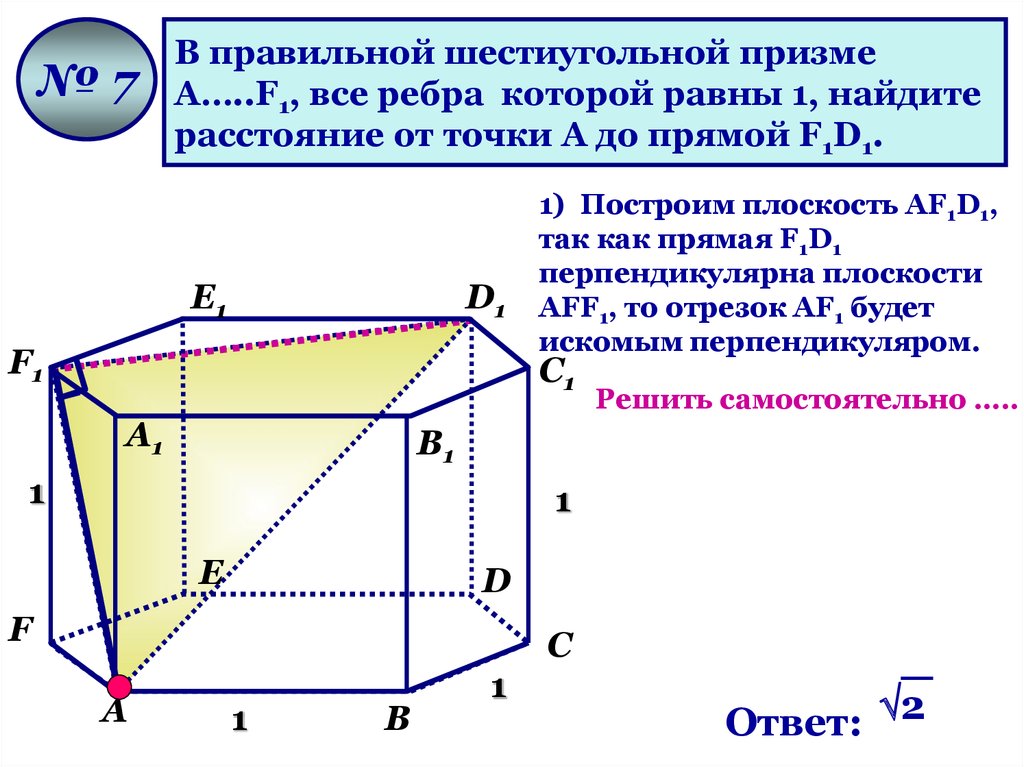
№7
В правильной шестиугольной призме
А…..F1, все ребра которой равны 1, найдите
расстояние от точки А до прямой F1D1.
Е1
D1
F1
1) Построим плоскость АF1D1,
так как прямая F1D1
перпендикулярна плоскости
АFF1, то отрезок АF1 будет
искомым перпендикуляром.
С1
А1
Решить самостоятельно …..
В1
1
1
Е
D
F
С
А
1
В
1
Ответ: 2

14.

№8
М А1
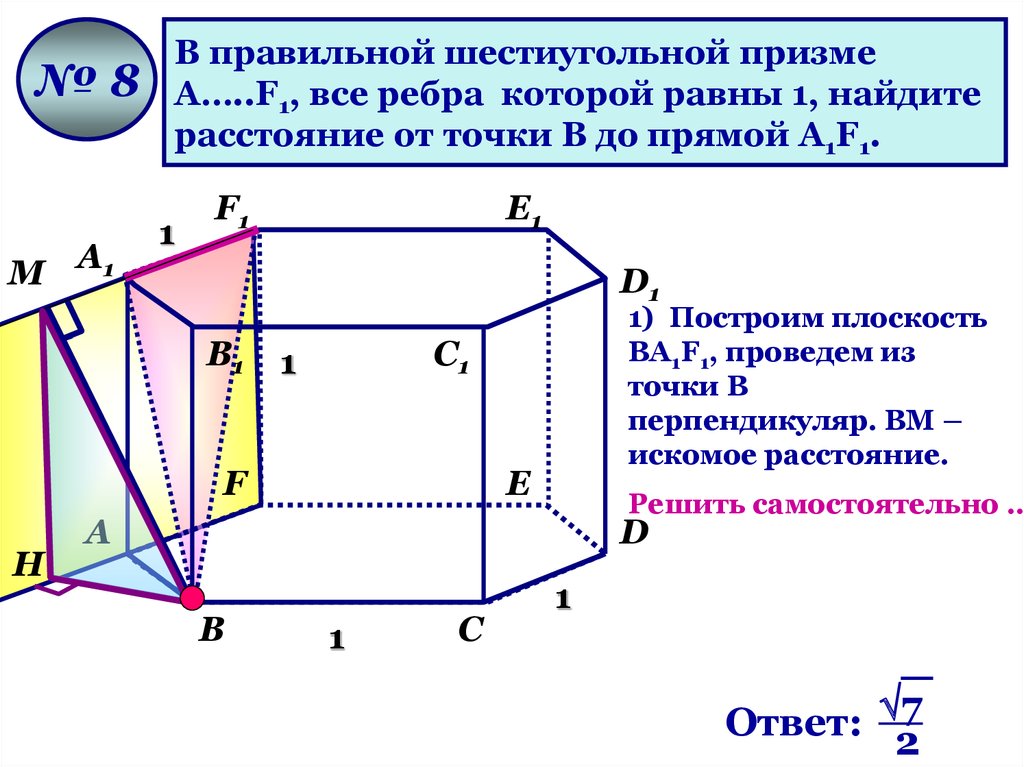
В правильной шестиугольной призме
А…..F1, все ребра которой равны 1, найдите
расстояние от точки В до прямой А1F1.
1
F1
Е1
D1
В1
С1
1
F
Н
1) Построим плоскость
ВА1F1, проведем из
точки В
перпендикуляр. ВМ –
искомое расстояние.
Е
Решить самостоятельно …
А
D
В
1
С
1
Ответ: 7
2

15.

Расстояние от точки
до плоскости

16.

Повторение:
А
М
Н
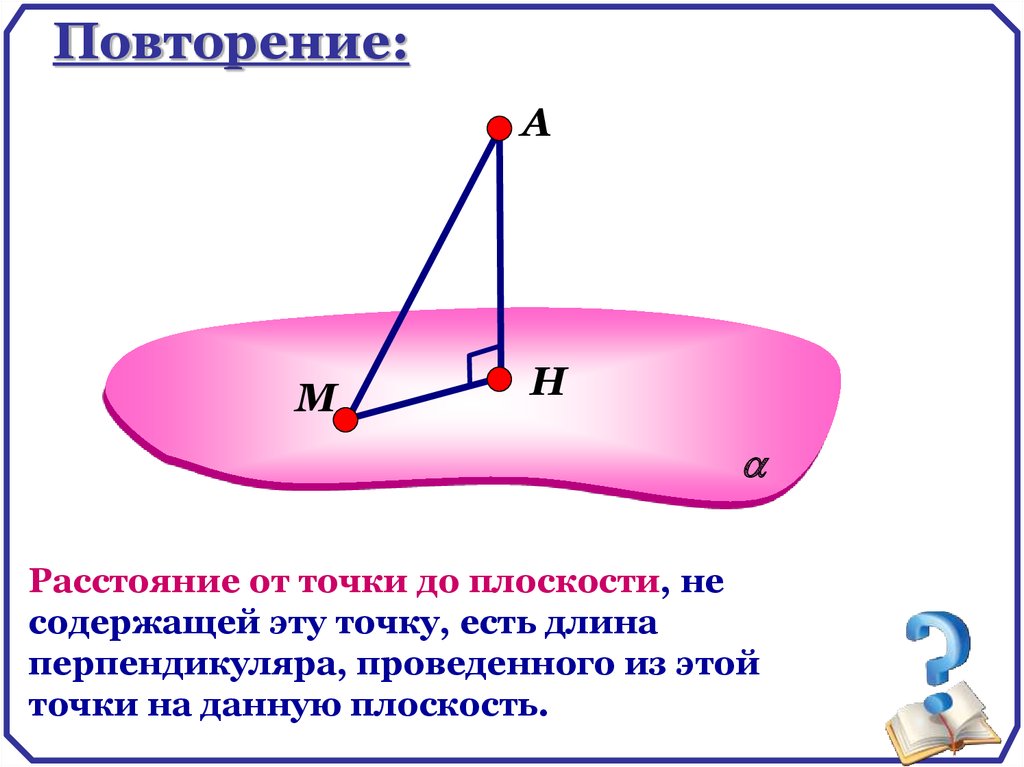
Расстояние от точки до плоскости, не
содержащей эту точку, есть длина
перпендикуляра, проведенного из этой
точки на данную плоскость.

17.

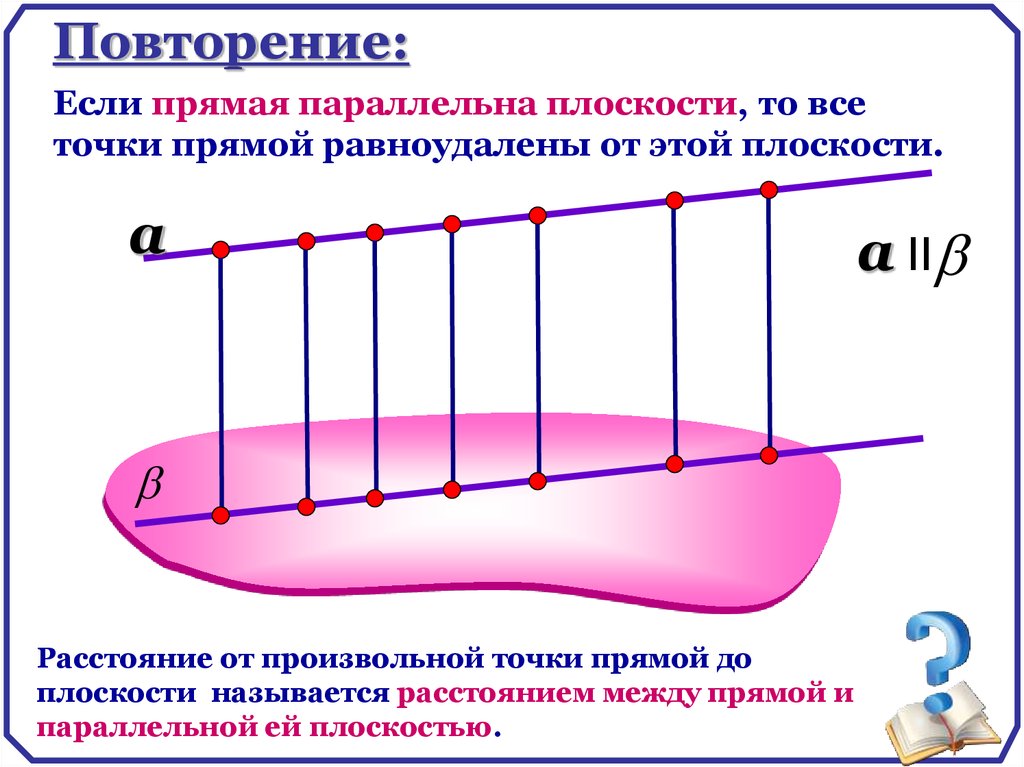
Повторение:
Если прямая параллельна плоскости, то все
точки прямой равноудалены от этой плоскости.
a
Расстояние от произвольной точки прямой до
плоскости называется расстоянием между прямой и
параллельной ей плоскостью.
a II

18.

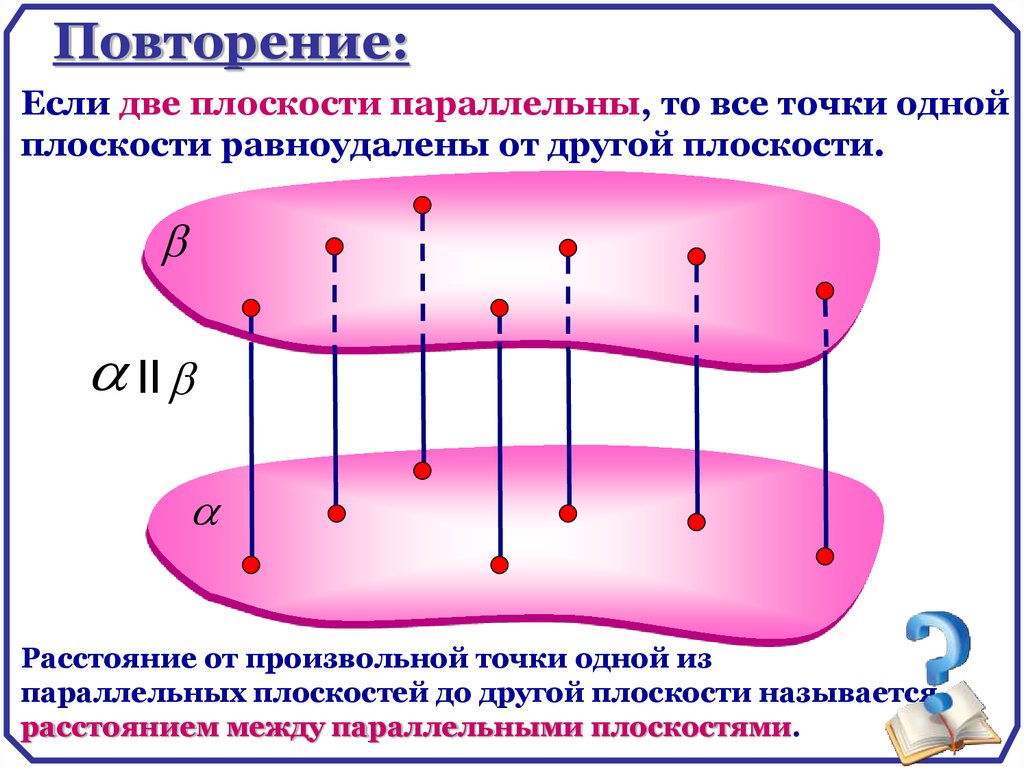
Повторение:
Если две плоскости параллельны, то все точки одной
плоскости равноудалены от другой плоскости.
II
Расстояние от произвольной точки одной из
параллельных плоскостей до другой плоскости называется
расстоянием между параллельными плоскостями.

19.

Повторение:
Расстояние от точки М до плоскости :
1) Равно расстоянию до плоскости от произвольной точки Р,
лежащей на прямой а, которая проходит ч/з точку М и
параллельна плоскости ;
2) Равно расстоянию до плоскости от произвольной точки
Р, лежащей на плоскости , которая проходит ч/з точку М и
параллельна плоскости ;
3) Находится с помощью координатно – векторного метода;

20.

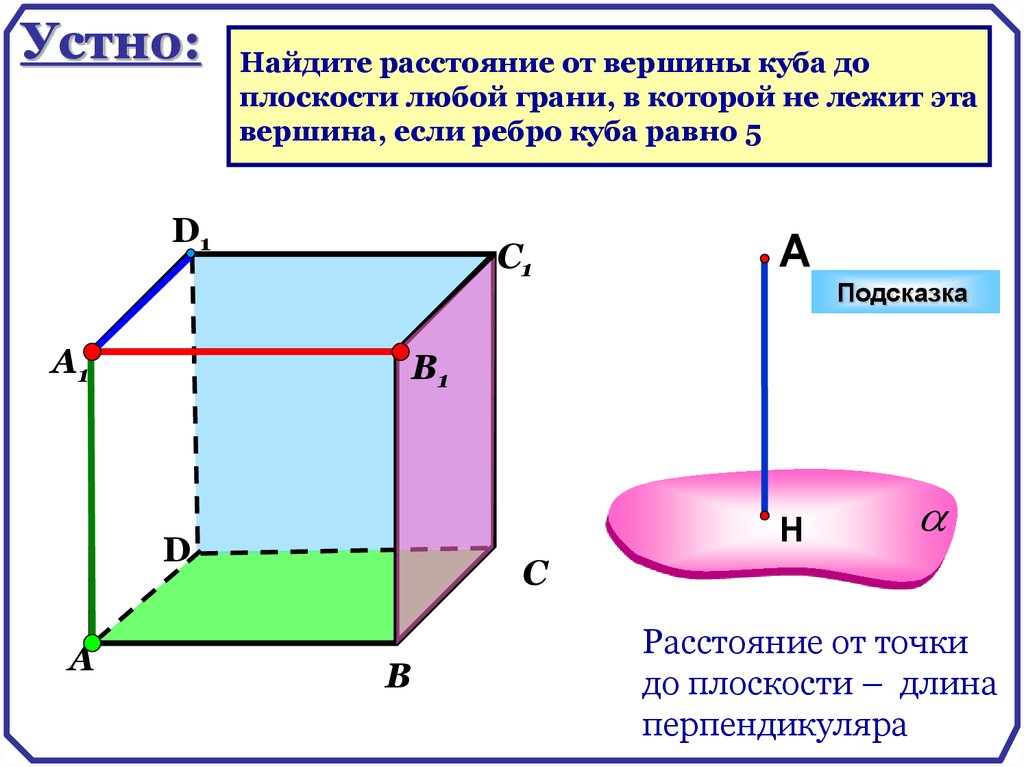
Устно:
Найдите расстояние от вершины куба до
плоскости любой грани, в которой не лежит эта
вершина, если ребро куба равно 5
D1
А1
С1
Подсказка
В1
Н
D
А
А
С
В
Расстояние от точки
до плоскости – длина
перпендикуляра

21.

Устно:
Дан прямоугольный параллелепипед
ABCДA1B1C1Д1, найдите расстояние между
прямой А1С1 и плоскостью АВС .
D1
С1
Подсказка
А1
В1
a
d
С
D
А
n
a II
В Расстояние от произвольной точки
прямой до плоскости называется расстоянием
между прямой и параллельной ей плоскостью

22.

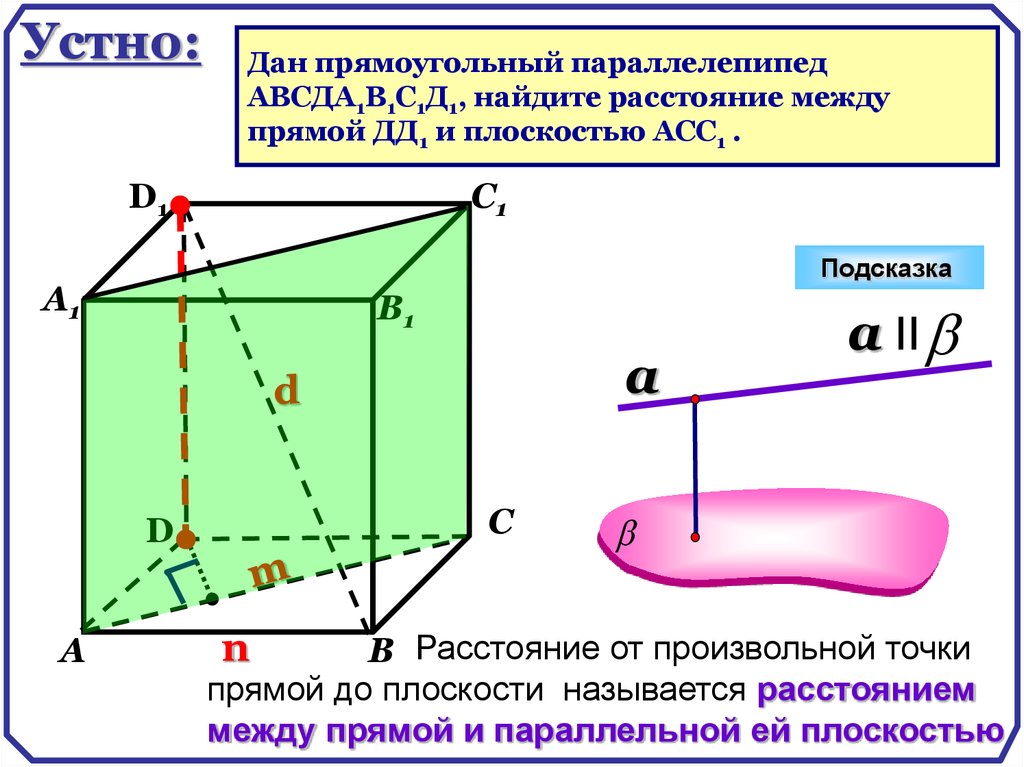
Устно:
Дан прямоугольный параллелепипед
ABCДA1B1C1Д1, найдите расстояние между
прямой ДД1 и плоскостью АСС1 .
D1
С1
Подсказка
А1
В1
a
d
С
D
А
n
a II
В Расстояние от произвольной точки
прямой до плоскости называется расстоянием
между прямой и параллельной ей плоскостью

23.

Устно:
Дан прямоугольный параллелепипед
ABCДA1B1C1Д1, найдите расстояние между
плоскостями АВВ1 иДСС1.
D1
С1
А1
Подсказка
II
В1
d
D
С
n
А
В
Расстояние от произвольной точки одной из параллельных
плоскостей до другой плоскости называется
расстоянием между параллельными плоскостями.

24.

В единичном кубе АВСДА1В1С1Д1 найдите
расстояние от точки А до плоскости ВДА1.
№1
1) Построим плоскость AА1С1С
С1 перпендикулярную плоскости
ДВА1.
D1
А1
В1
1
М
D
1
А
ВД ДВА 1
ВД АС ДВА 1 АА1С1С
ВД АА1
2
2
С
О
1
В
проведем из точки А
перпендикуляр. АМ – искомое
расстояние.
2) Найдем искомое расстояние
через вычисление площади
треугольника AА1О.
Ответ: 3
3

25.

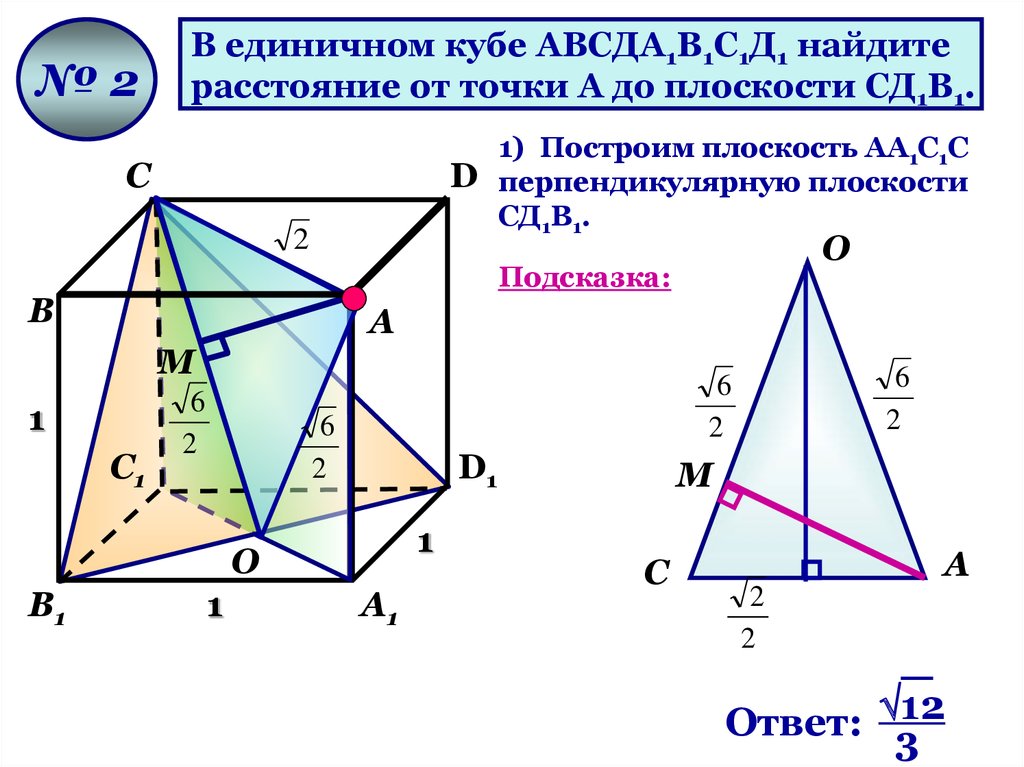
№2
В единичном кубе АВСДА1В1С1Д1 найдите
расстояние от точки А до плоскости СД1В1.
1) Построим плоскость AА1С1С
D перпендикулярную плоскости
СД1В1.
С
2
Подсказка:
В
А
М
1
С1
6
2
6
2
1
6
2
6
2
D1
1
О
В1
О
А1
М
С
А
2
2
Ответ: 12
3

26.

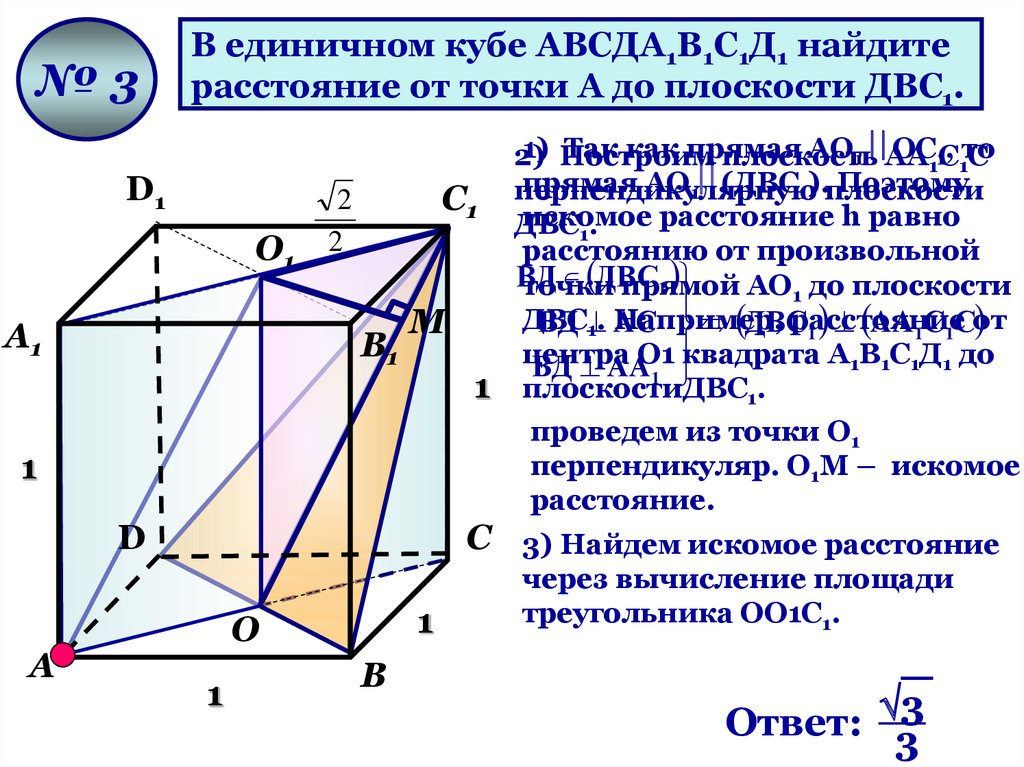
№3
В единичном кубе АВСДА1В1С1Д1 найдите
расстояние от точки А до плоскости ДВС1.
D1
О1
А1
1
1) Построим
Так как прямая
АО1 ОС
2)
плоскость
AА11С, 1то
С
прямая АО1 (ДВС1).плоскости
Поэтому
перпендикулярную
2
С1 искомое расстояние h равно
ДВС1.
2
расстоянию от произвольной
ВД
ДВС
1
точки
прямой
АО1 до плоскости
ДВС
.
Например,
расстояние
от
ВД
АС
М
1
ДВС
1 АА 1С1С
В1
центра
квадрата А1В1С1Д1 до
ВД ААО1
1
1 плоскостиДВС
1.
проведем из точки О1
перпендикуляр. О1М – искомое
расстояние.
D
А
С 3) Найдем искомое расстояние
1
О
1
В
через вычисление площади
треугольника ОО1С1.
Ответ: 3
3

27.

№4
В правильной шестиугольной пирамиде
SАВСDЕF, стороны основания которой
равны 1, а боковые ребра равны 2,найдите
расстояние от точки А до прямой SВС.
1)
как
АД ВС,
то ВС
2) Так
Пусть
К прямая
– середина
отрезка
прямая АД
(SВС). Поэтому
Построим
плоскость
SОК
искомое
расстояние
h равно
перпендикулярную плоскости
расстоянию от произвольной
SВС.
точки прямой АД до плоскости
ВСНапример,
SВC
SВС.
расстояние от
до плоскости
2центра
SOK
ВC ООК
SBC SВС.
S
2
Е
ВС SО
проведем из точки О
перпендикуляр. ОМ –
С искомое расстояние.
DМ
1 О
F
А
1
В
К1
Ответ: 15
5

28.

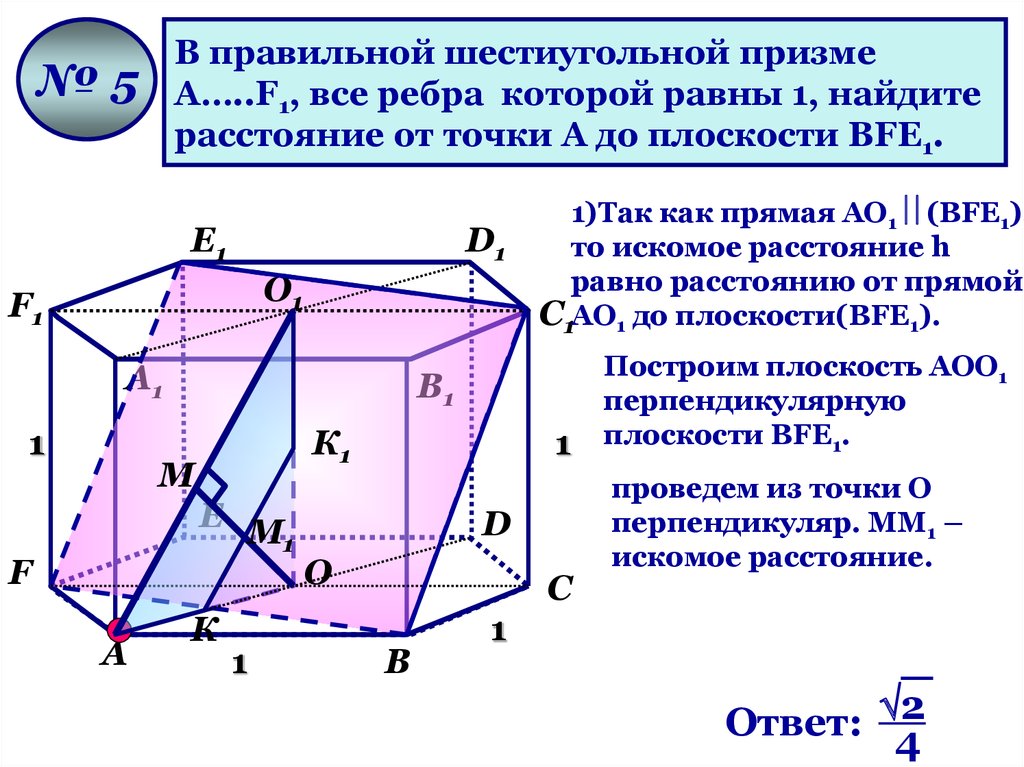
В правильной шестиугольной призме
А…..F1, все ребра которой равны 1, найдите
расстояние от точки А до плоскости ВFЕ1.
№5
Е1
D1
О1
F1
А1
1
В1
К1
М
Е М
1
F
А
1)Так как прямая АО1 (ВFЕ1),
то искомое расстояние h
равно расстоянию от прямой
С1АО1 до плоскости(ВFЕ1).
К
1
1
D
О
С
В
Построим плоскость АОО1
перпендикулярную
плоскости ВFЕ1.
проведем из точки О
перпендикуляр. ММ1 –
искомое расстояние.
1
Ответ: 2
4

29.

Расстояние между
скрещивающимися
прямыми

30.

Повторение:
Если две прямые скрещиваются, то через каждую из них
проходит плоскость, параллельная другой прямой, и притом
только одна.
a
a
b
a II
b
Расстояние между одной из скрещивающихся прямых и
плоскостью, проходящей через другую прямую
параллельно первой, называется расстоянием между
скрещивающимися прямыми.

31.

Повторение:
В
А
Отрезок, имеющий концы на двух скрещивающихся
прямых и перпендикулярный к этим прямым,
называется их общим перпендикуляром.
На рисунке АВ – общий перпендикуляр.

32.

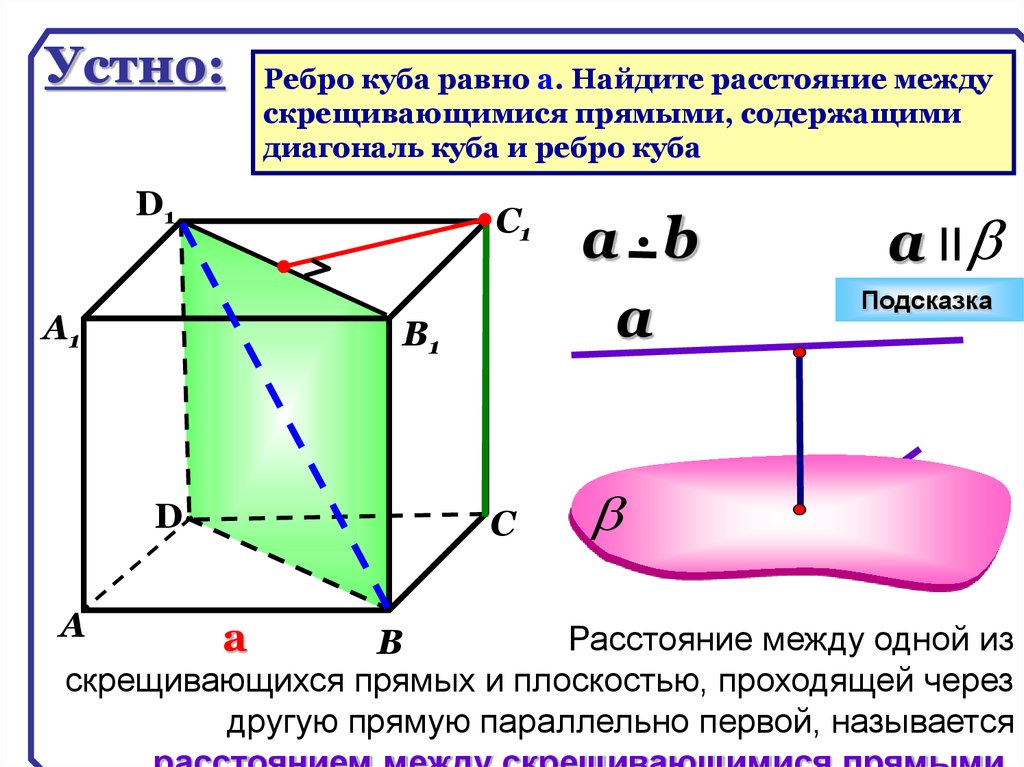
Устно:
Ребро куба равно а. Найдите расстояние между
скрещивающимися прямыми, содержащими
диагональ куба и ребро куба
D1
С1
А1
В1
D
А
С
а
a b
a
a II
Подсказка
b
Расстояние между одной из
В
скрещивающихся прямых и плоскостью, проходящей через
другую прямую параллельно первой, называется

33.

Устно:
Ребро куба равно а. Найдите расстояние между
скрещивающимися прямыми, содержащими
диагональ куба и диагональ грани куба
D1
С1
А1
В1
С
D
А
а
a b
a
a II
Подсказка
b
В
Расстояние между одной из
скрещивающихся прямых и плоскостью, проходящей через
другую прямую параллельно первой, называется

34.

№1
В правильной четырехугольной пирамиде
SАВСД, все ребра которой равны 1, найдите
расстояние между прямыми ВС и SА.
S
1
1М
D
Е
А
О
1
В
1) Прямая ВС параллельна
плоскости SAD, в которой лежит
прямая SA. расстояние между
прямыми ВС и SА равно
расстоянию от прямой ВС до
плоскости SAD.
Пусть К середина ребра
ВС. Построим плоскость
SКЕ перпендикулярную
С плоскости SAD, в
которой лежит прямая
SA.
1
Проведем из точки К
перпендикуляр. КМ – искомое
расстояние.
Ответ: 6
3

35.

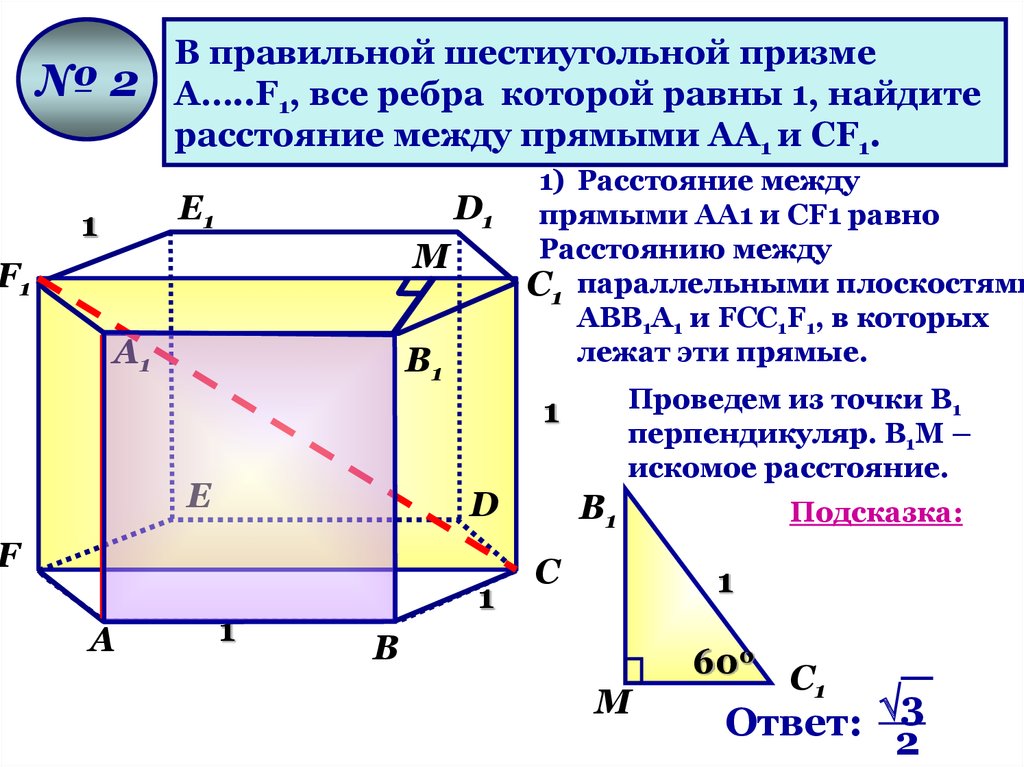
№2
В правильной шестиугольной призме
А…..F1, все ребра которой равны 1, найдите
расстояние между прямыми АА1 и СF1.
Е1
1
D1
М
F1
А1
В1
1) Расстояние между
прямыми АА1 и СF1 равно
Расстоянию между
С1 параллельными плоскостями
АВВ1А1 и FCC1F1, в которых
лежат эти прямые.
Проведем из точки В1
перпендикуляр. В1М –
искомое расстояние.
1
Е
D
F
А
1
1
В1
С
Подсказка:
1
В
600
М
С1
Ответ: 3
2

36.

В единичном кубе АВСДА1В1С1Д1 найдите
расстояние между прямыми АВ1 и ВС1.
№3
D1
С1
О1
В1
А1
М
1
Н
1
D
С
О
А
1
1
2)
1) Диагональ
Через прямые
кубаАВ
СА11и ВС1
перпендикулярна
построим плоскости
этим
AВ1D1 и
плоскостям,
ВДС1,
А длина отрезка МН
будет
расстоянию
между
ВСравна
ΙΙ
АД
1
1
прямыми АВ 1 и ВС1.
АВ1 ΙΙ ДС1
Подсказка: АД 1В1 ΙΙ ДВС1
ВС
ДС=1 НС
А1М
=1МН
АД 1 АВ1
Расстояние между этими
прямыми равно расстоянию
между соответствующими
плоскостями AВ1D1 и ВДС1.
В
Ответ: 3
3

37.

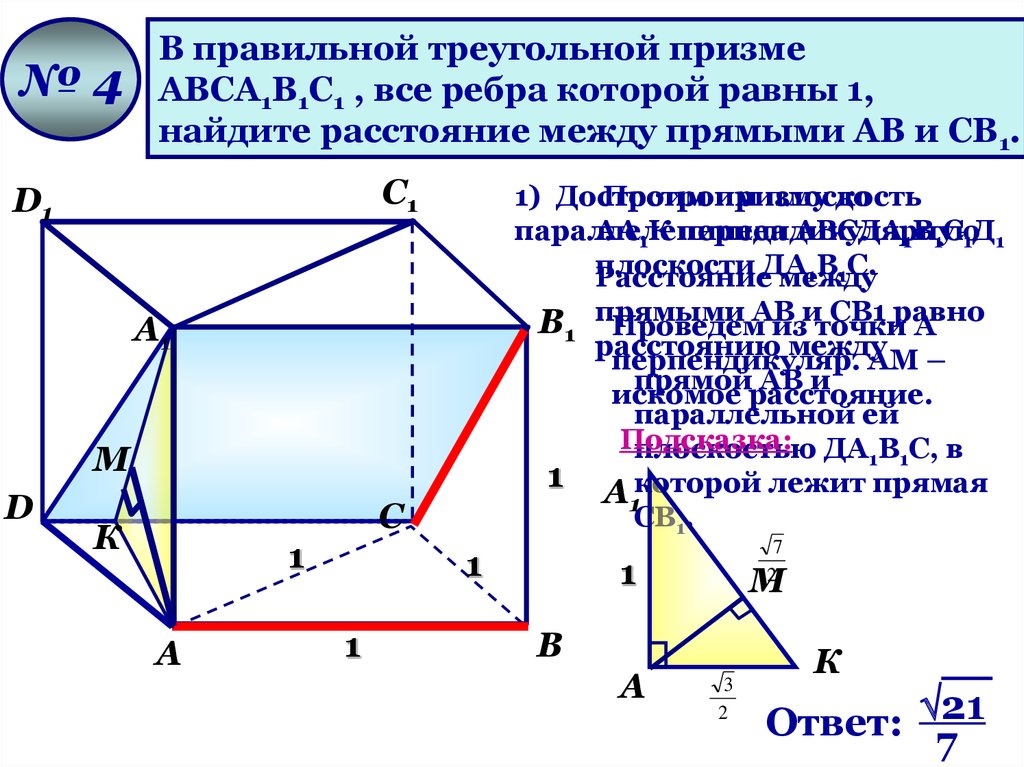
№4
В правильной треугольной призме
АВСА1В1С1 , все ребра которой равны 1,
найдите расстояние между прямыми АВ и СВ1.
С1
D1
1) Достроим
Построим
призму
плоскость
до
параллелепипеда
АА1К перпендикулярную
АВСДА1В1С1Д1
плоскости
1В1С.
РасстояниеДА
между
СВ1 равно
В1 прямыми
ПроведемАВ
изиточки
А
А1
М
D
1
С
К
1
А
1
1
расстоянию
между
перпендикуляр.
АМ –
прямой
АВ
и
искомое расстояние.
параллельной ей
Подсказка:
плоскостью ДА1В1С, в
А1которой лежит прямая
СВ1.
7
2
1
М
В
А
3
2
К
Ответ: 21
7

38.

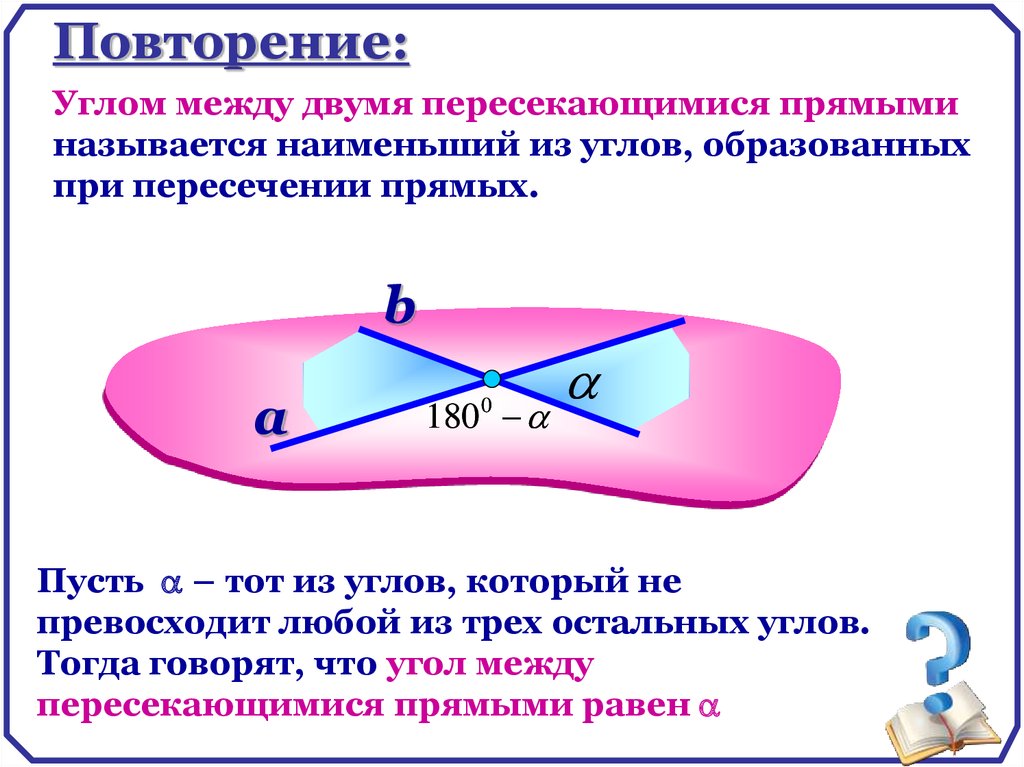
Угол между прямыми

39.

Повторение:
Углом между двумя пересекающимися прямыми
называется наименьший из углов, образованных
при пересечении прямых.
b
a
180
0
Пусть – тот из углов, который не
превосходит любой из трех остальных углов.
Тогда говорят, что угол между
пересекающимися прямыми равен

40.

Повторение:
Углом между скрещивающимися прямыми называется угол
между пересекающимися прямыми, соответственно
параллельными данным скрещивающимися.
b
a
n
m
M
a
b
Через произвольную точку М проведем прямые m и n,
соответственно параллельные прямым a и b.
Угол между скрещивающимися прямыми a и b равен

41.

Повторение:
Углом между скрещивающимися прямыми называется угол
между пересекающимися прямыми, соответственно
параллельными данным скрещивающимися.
b
a
m
M
a
b
Точку М можно выбрать произвольным образом.
В качестве точки М удобно взять любую точку на одной
из скрещивающихся прямых.

42.

Повторение:
При нахождении угла между прямыми
используют
1) Формулу
cos
b2 c2 a2
2bc
(теорема косинусов)
для нахождения угла между прямыми m и n, если стороны
a и b треугольника АВС соответственно параллельны этим
прямым;
2) Или в координатной форме:
cos
х1 х 2 у 1 у 2 z 1 z 2
x12 y 12 z 12 x 22 y 22 z 22
3) Ключевые задачи;

43.

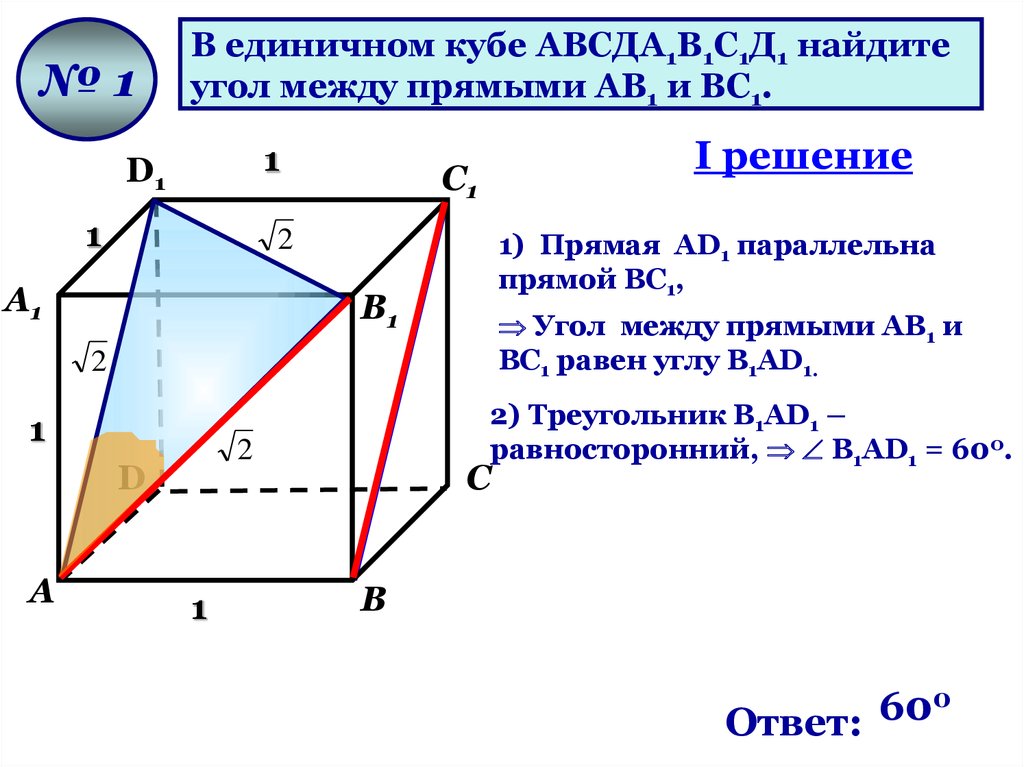
№1
В единичном кубе АВСДА1В1С1Д1 найдите
угол между прямыми АВ1 и ВС1.
1
D1
1
I решение
С1
2
А1
1) Прямая AD1 параллельна
прямой ВС1,
В1
Угол между прямыми АВ1 и
ВС1 равен углу В1AD1.
2
1
2
D
А
2) Треугольник В1AD1 –
равносторонний, В1AD1 = 600.
1
С
В
0
60
Ответ:

44.

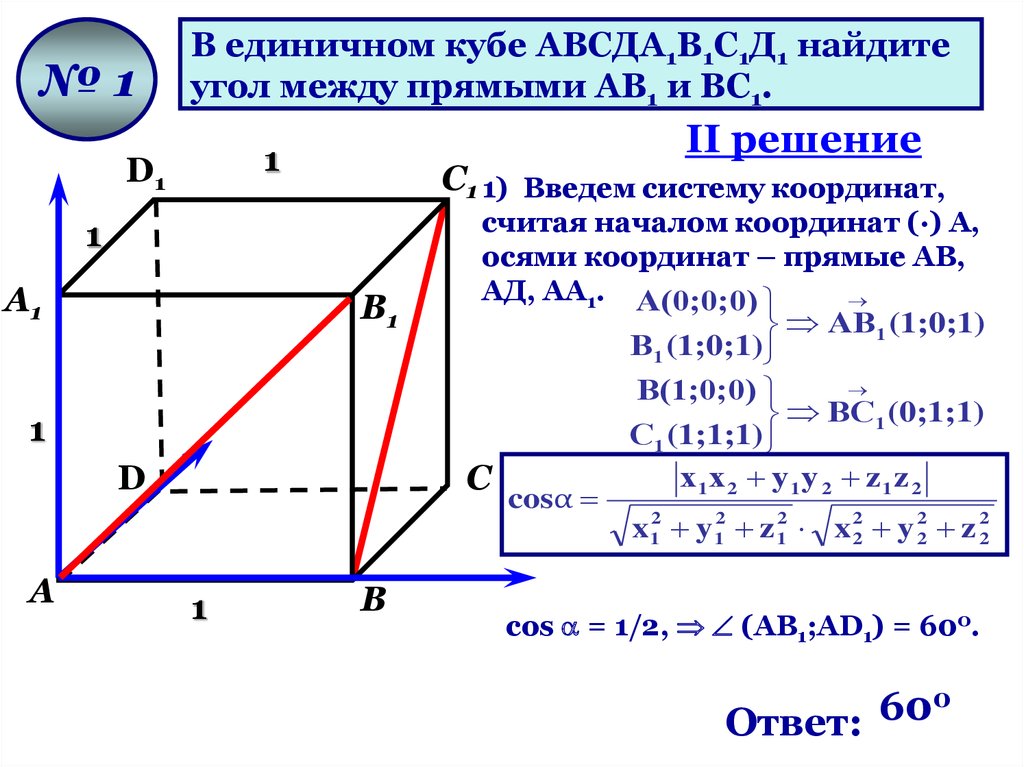
№1
В единичном кубе АВСДА1В1С1Д1 найдите
угол между прямыми АВ1 и ВС1.
II решение
1
D1
С1 1) Введем систему координат,
1
А1
В1
1
D
А
1
В
считая началом координат (·) А,
осями координат – прямые АВ,
АД, АА1. А(0;0;0)
АВ1 (1;0;1)
В1 (1;0;1)
В(1;0;0)
ВС1 (0;1;1)
С1 (1;1;1)
х1 х 2 у 1 у 2 z 1 z 2
С
cosα
x12 y 12 z 12 x 22 y 22 z 22
cos = 1/2, (АВ1;AD1) = 600.
0
60
Ответ:

45.

В единичном кубе АВСДА1В1С1Д1 найдите
угол между прямыми А1Д и Д1Е,
где Е – середина ребра СС1.
№2
I решение
D1
С1 1) Прямая A М параллельна
1
прямой ВС1
А1
Угол между прямыми А1D и
Д1Е равен углу МA1D.
В1
Е 2) из ∆МA1D по теореме
косинусов:
D
А
М
В
С
cosα
b2 c2 a2
2bc
1
Ответ: α arccos
10

46.

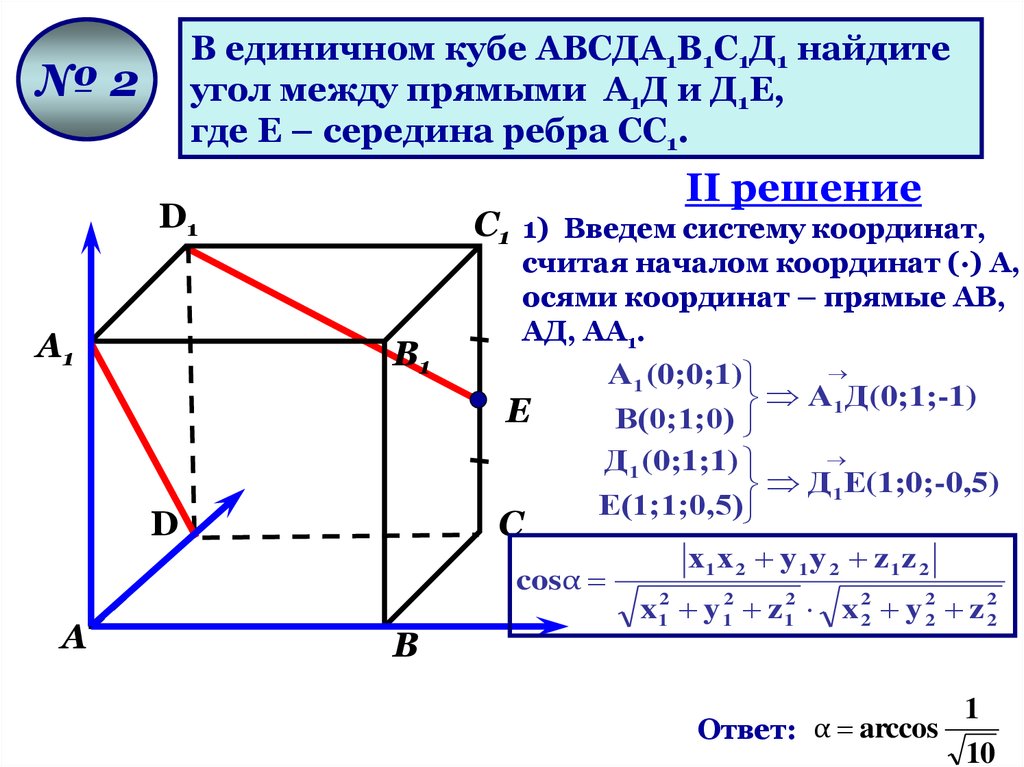
В единичном кубе АВСДА1В1С1Д1 найдите
угол между прямыми А1Д и Д1Е,
где Е – середина ребра СС1.
№2
II решение
D1
А1
С1 1) Введем систему координат,
В1
D
считая началом координат (·) А,
осями координат – прямые АВ,
АД, АА1.
А 1 (0;0;1)
А 1 Д(0;1;-1)
Е
В(0;1;0)
Д 1 (0;1;1)
Д 1Е(1;0;-0,5)
Е(1;1;0,5)
С
cosα
А
В
х1 х 2 у 1 у 2 z 1 z 2
x12 y 12 z 12 x 22 y 22 z 22
Ответ: α arccos
1
10

47.

В правильной треугольной призме
ABCA1B1C1 ,все ребра которой равны 1,
найдите косинус угла между прямыми
АВ и A1C .
1
В1 1) Прямая A В параллельна
№3
А1
прямой АВ,
2
1
Угол между прямыми АВ и
А1С равен углу СA1В1.
С1
1
1
2) из ∆ СA1В1 по теореме
косинусов:
2
В
А
cosα
b2 c2 a2
2bc
1
С
Ответ: 2
4

48.

№4
В правильной треугольной призме
ABCA1B1C1,все ребра которой равны 1,найдите
косинус угла между прямыми АВ1 и ВС1 .
С1
М
А1
В1
С
М
А
1
1
В
11
Ответ: 4

49.

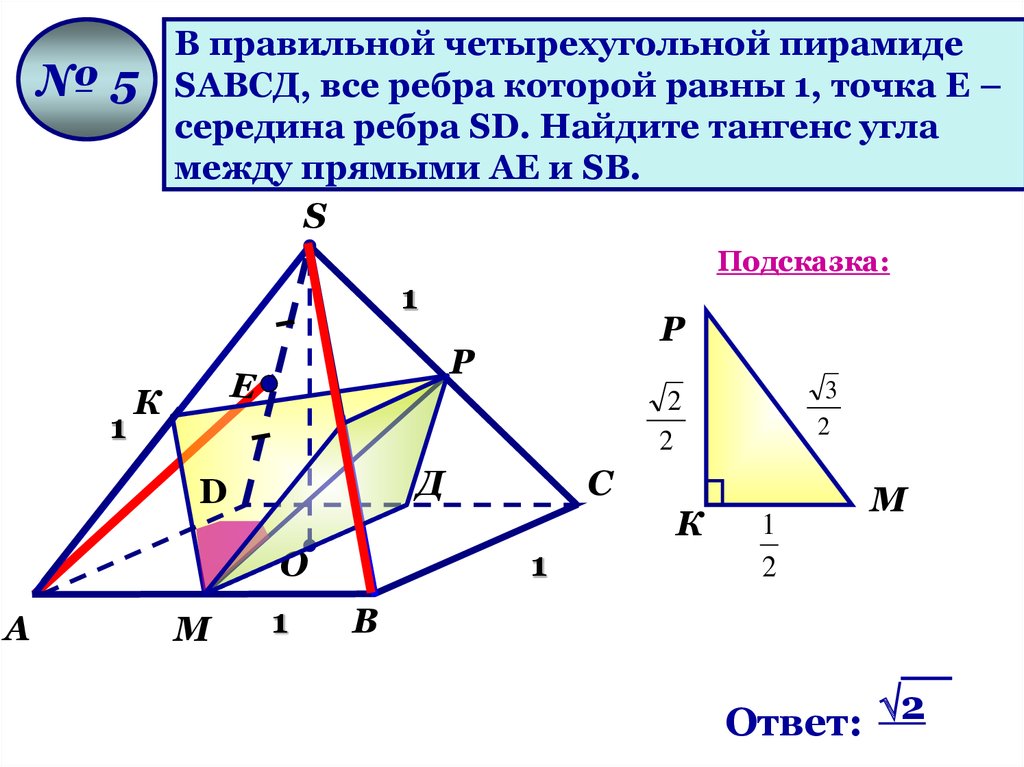
№5
В правильной четырехугольной пирамиде
SАВСД, все ребра которой равны 1, точка Е –
середина ребра SD. Найдите тангенс угла
между прямыми АЕ и SВ.
S
Подсказка:
1
Р
Р
1
К
Д
D
М
С
К
О
А
3
2
2
2
1
1
1
2
М
В
Ответ: 2

50.

№6
В правильной шестиугольной призме A … F1,
все ребра которой равны 1, найдите
косинус угла между прямыми AB1 и BC1
Е1
D1
О1
F1
1
А1
В1
2
1
2
Е
D
О
F
А
1
1) Построим плоскость
АА1D1D параллельную
плоскости ВВ1С1С. Тогда
С1 прямая AO1 параллельна
прямой BC1, и искомый
угол φ между прямыми AB1 и
BC1 равен B1AO1.
С
В
1
Ответ: 0,75

51.

Угол между прямой
и плоскостью

52.

Повторение:
Углом между прямой и плоскостью, пересекающей
эту прямую и не перпендикулярной к ней,
называется угол между прямой и ее проекцией на
плоскость.
М
перпендикуляр
А
проекция Н

53.

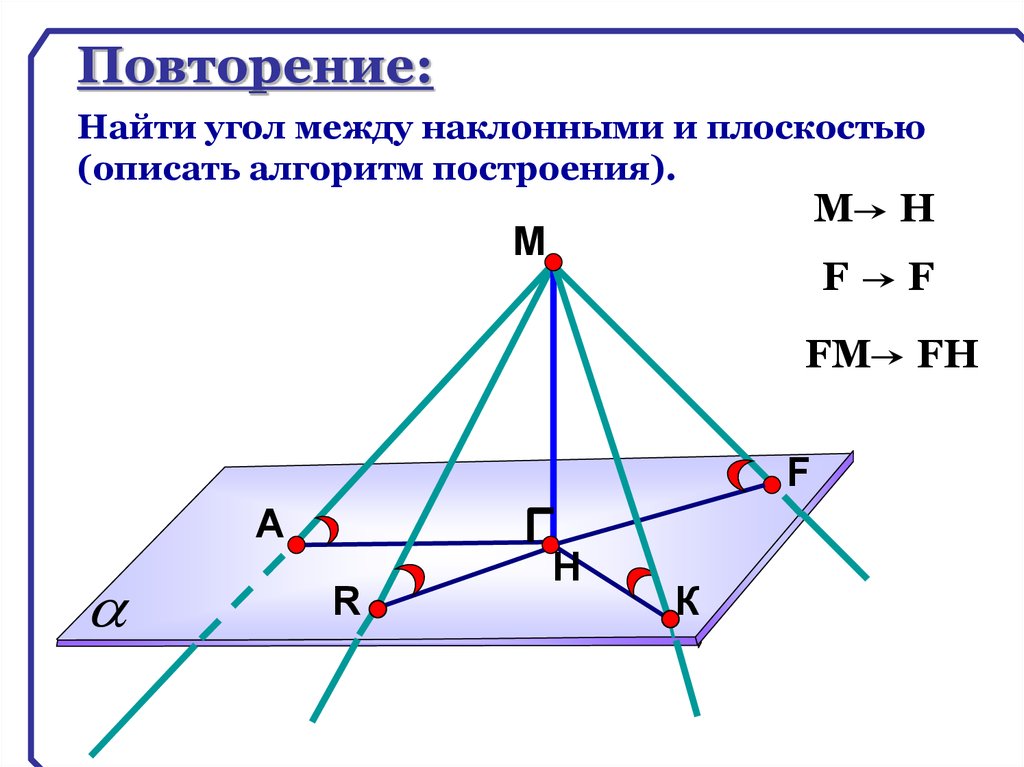
Повторение:
Найти угол между наклонными и плоскостью
(описать алгоритм построения).
М
М
H
F
F
FМ
F
А
R
Н
К
FH

54.

Повторение:
Угол между прямой m и плоскостью можно
вычислить:
1) Если этот угол удается включить в прямоугольный
треугольник в качестве одного из острых углов;
2) Используя векторный метод;
3) Используя координатно –векторный метод;
4) Используя ключевые задачи;

55.

Устно:
Найдите тангенс угла между диагональю куба и
плоскостью одной из его граней.
D1
перпендикуляр
А1
А
С1
Подсказка
В1
М
D
В
перпендикуляр
С
А
Н
проекция
Углом между прямой и плоскостью, пересекающей
эту прямую и не перпендикулярной к ней,
называется угол между прямой и ее проекцией на

56.

№1
В единичном кубе АВСДА1В1С1Д1 найдите
тангенс угла между прямой АА1 и
плоскостью ВС1Д .
D1
С1 1) Прямая AА1 параллельна
1
А1
В1
1
2
2
D
О
А
1
В
прямой СС1, Угол между
прямой АА1 и плоскостью ВС1Д .
равен углу между СС1 и
плоскостью ВС1Д.
ВД ДВС1
1
ВД АС ДВС1 ОС1С
ВД СС1
С 2. Прямая СС проецируется на
1
плоскость ВС1Д в прямую ОС1.
Поэтому проекция точки С
лежит на отрезке ОС1. Значит,
прямая ОС1 является проекцией
прямой СС1, следовательно, угол
ОС1С искомый.
Ответ: 2
2

57.

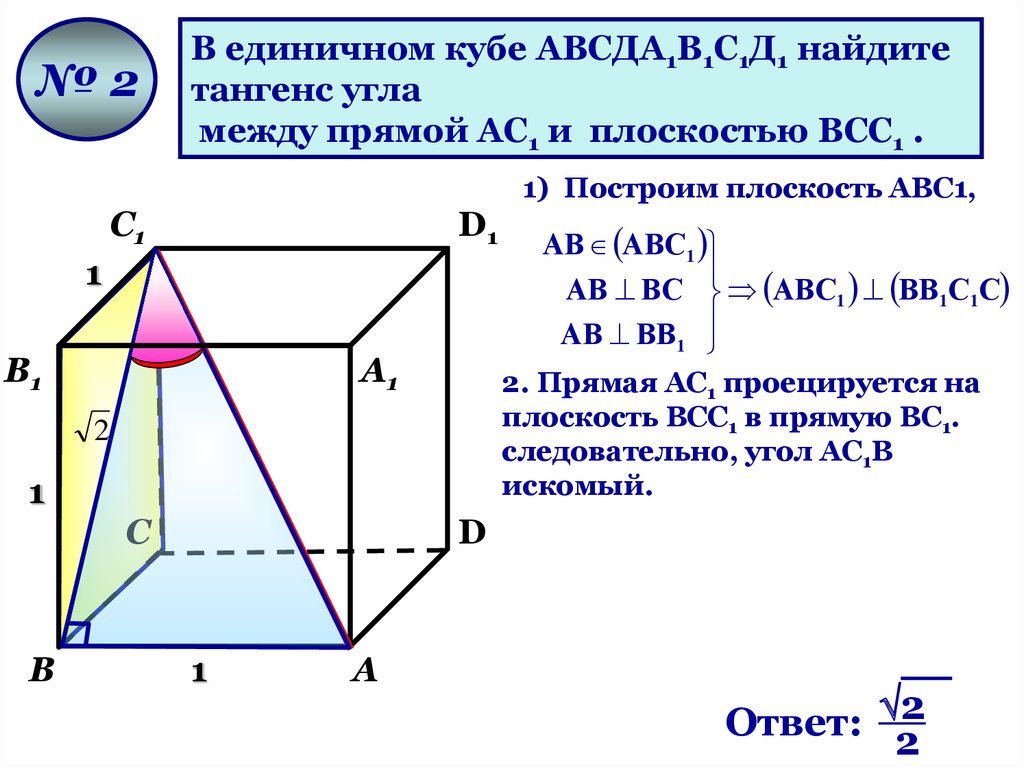
№2
В единичном кубе АВСДА1В1С1Д1 найдите
тангенс угла
между прямой АС1 и плоскостью ВСС1 .
1) Построим плоскость AВС1,
С1
D1
1
В1
А1
2. Прямая АС1 проецируется на
плоскость ВСС1 в прямую ВС1.
следовательно, угол АС1В
искомый.
2
1
С
В
АВ АВС1
АВ ВС АВС1 ВВ1С1С
АВ ВВ1
D
1
А
Ответ: 2
2

58.

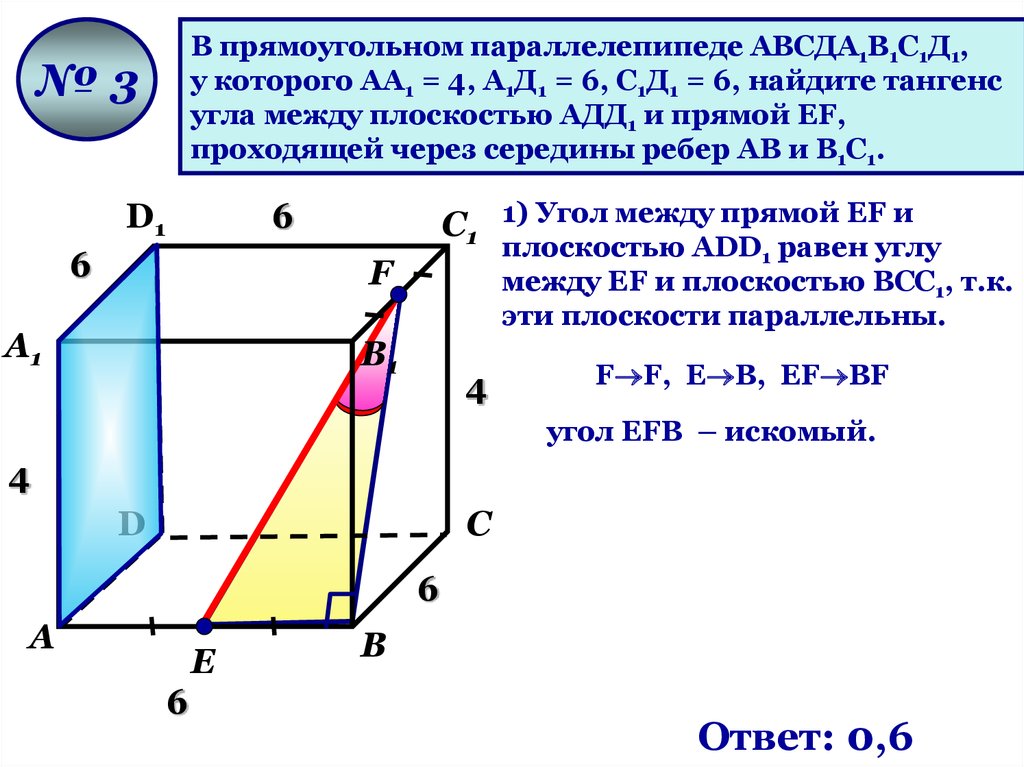
В прямоугольном параллелепипеде АВСДА1В1С1Д1,
у которого АА1 = 4, А1Д1 = 6, С1Д1 = 6, найдите тангенс
угла между плоскостью АДД1 и прямой ЕF,
проходящей через середины ребер АВ и В1С1.
№3
D1
С1 1) Угол между прямой EF и
6
6
плоскостью АDD1 равен углу
между EF и плоскостью ВСС1, т.к.
эти плоскости параллельны.
F
А1
В1
4
F F, Е В, ЕF ВF
угол EFB – искомый.
4
D
С
6
А
Е
6
В
Ответ: 0,6

59.

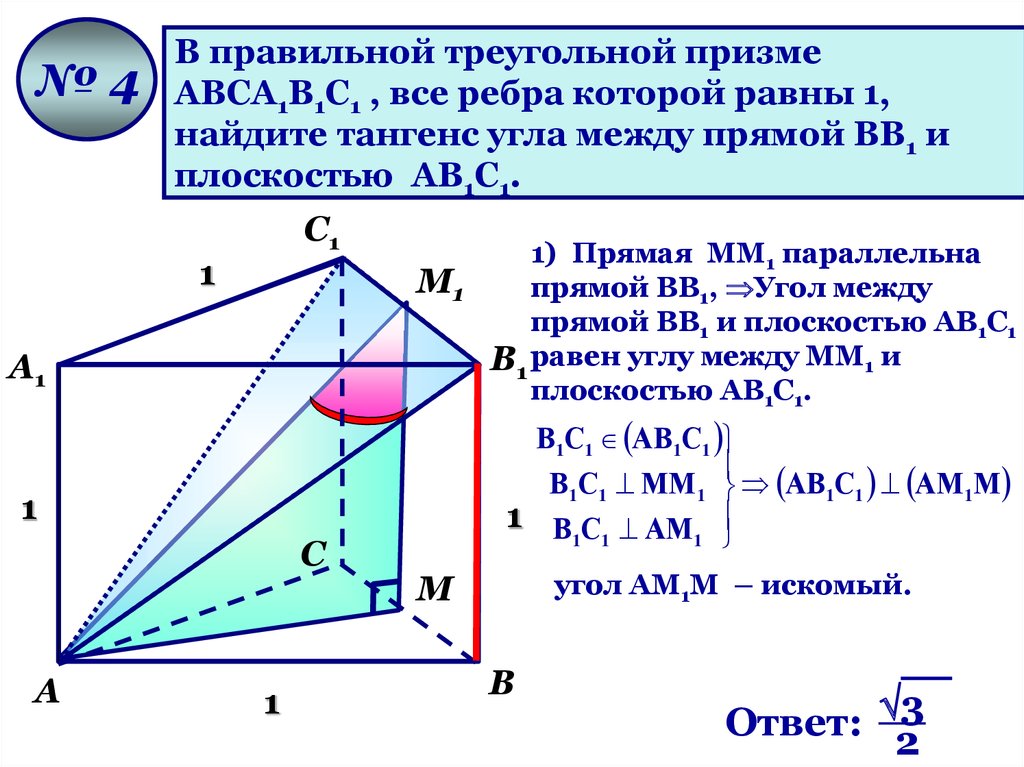
№4
В правильной треугольной призме
АВСА1В1С1 , все ребра которой равны 1,
найдите тангенс угла между прямой ВВ1 и
плоскостью АВ1С1.
С1
1
М1
А1
В1С1 АВ1С1
В1С1 ММ 1 АВ1С1 АМ 1М
1 В С АМ
1 1
1
1
С
А
1
1) Прямая ММ1 параллельна
прямой ВВ1, Угол между
прямой ВВ1 и плоскостью АВ1С1
В1 равен углу между ММ1 и
плоскостью АВ1С1.
угол АМ1М – искомый.
М
В
Ответ: 3
2

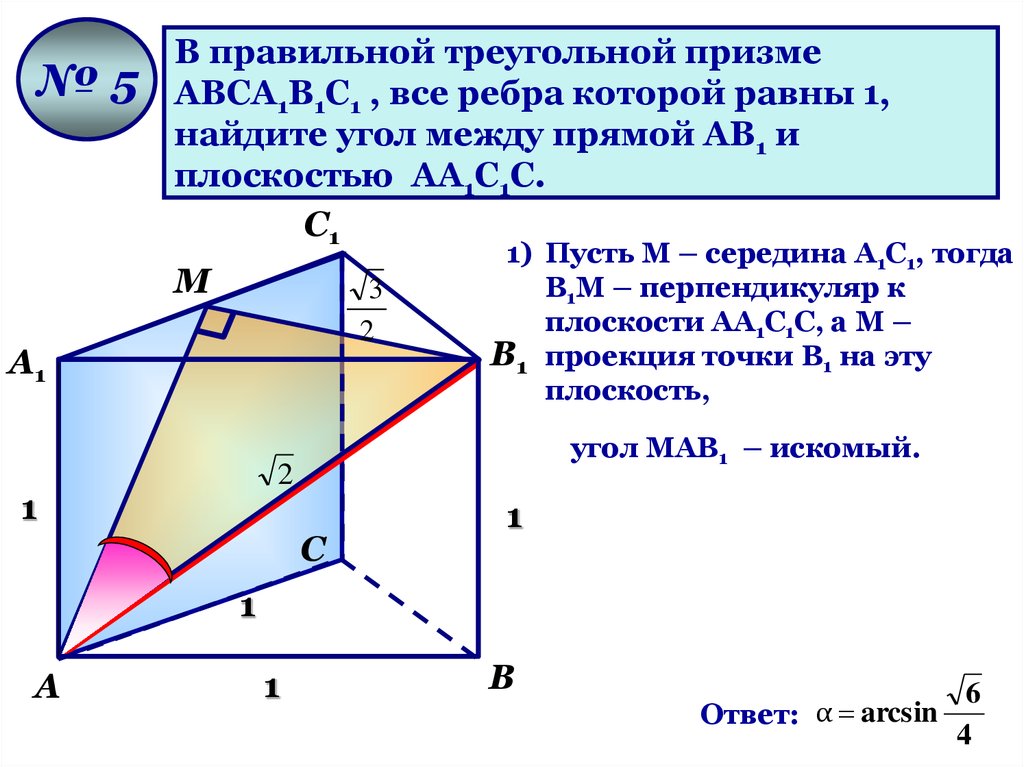
60.

№5
В правильной треугольной призме
АВСА1В1С1 , все ребра которой равны 1,
найдите угол между прямой АВ1 и
плоскостью АА1С1С.
С1
М
3
2
А1
1) Пусть М – середина А1С1, тогда
В1М – перпендикуляр к
плоскости АА1С1С, а М –
В1 проекция точки В1 на эту
плоскость,
угол МАВ1 – искомый.
2
1
С
1
1
А
1
В
Ответ: α arcsin
6
4

61.

№6
В правильной четырехугольной пирамиде
SАВСД, все ребра которой равны 1. Найдите
синус угла между прямой ВД и плоскостью SВС.
S
Подсказка:
К
1
К
1
Д
О
А
1
1
2
С
D
1
В
3
2
В
О
2
2
Ответ: 3
3

62.

Угол между
плоскостями

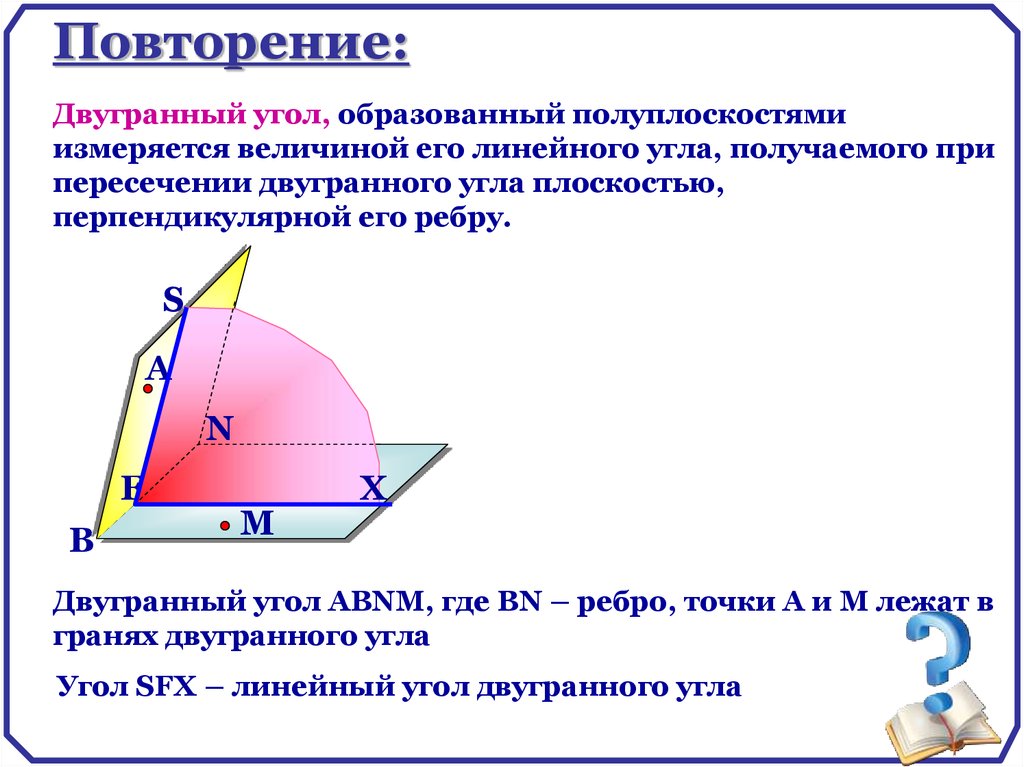
63.

Повторение:
Двугранный угол, образованный полуплоскостями
измеряется величиной его линейного угла, получаемого при
пересечении двугранного угла плоскостью,
перпендикулярной его ребру.
S
А
N
F
В
М
X
Двугранный угол АВNМ, где ВN – ребро, точки А и М лежат в
гранях двугранного угла
Угол SFX – линейный угол двугранного угла

64.

Повторение:
Алгоритм построения линейного угла.
D
Угол РОК – линейный угол
двугранного угла РDEК.
Р
О
К
E
Плоскость линейного угла (РОК) DE.

65.

Повторение:
Угол между пересекающимися плоскостями
можно вычислить:
1) Как угол между прямыми, лежащими в этих плоскостях и
перпендикулярными к линии их пересечения;
2) Как угол треугольника, если удается включить линейный
угол в некоторый треугольник;
3) Используя координатно –векторный метод;
4) Используя ключевые задачи;

66.

Устно:
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
АС ВМ
перпендикуляр
В
К
TTП
АС NМ
А
M
N проекция
С
Угол ВMN – линейный угол двугранного угла ВАСК

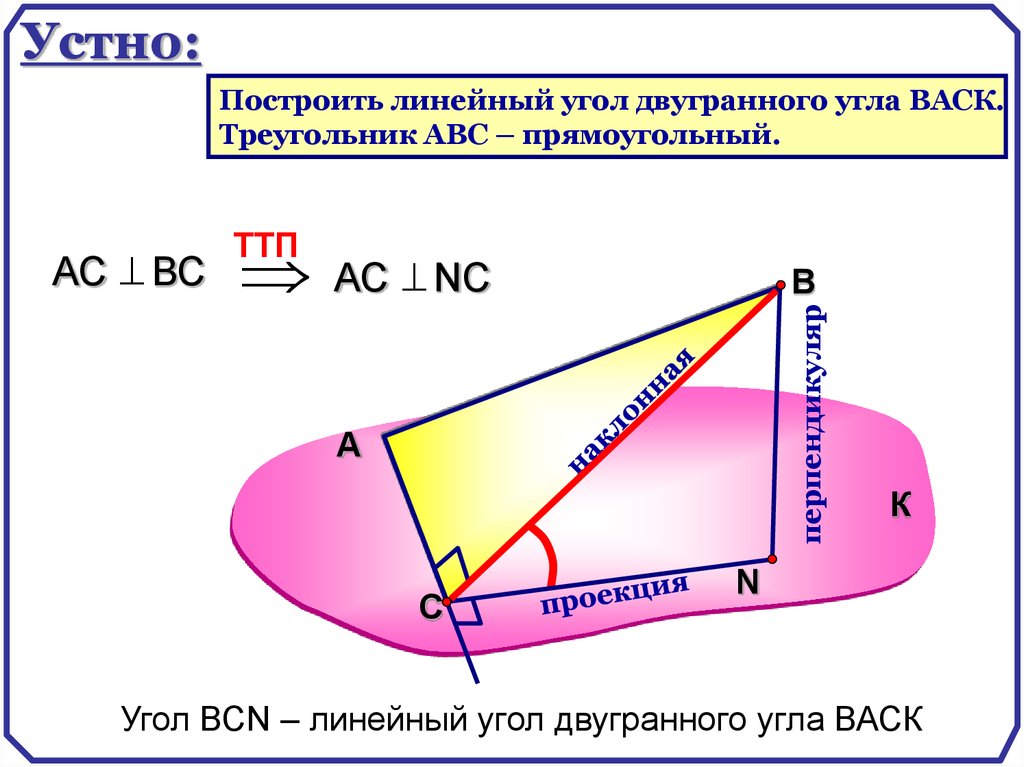
67.

Устно:
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
АС NС
В
перпендикуляр
АС ВС
TTП
А
С
К
N
Угол ВСN – линейный угол двугранного угла ВАСК

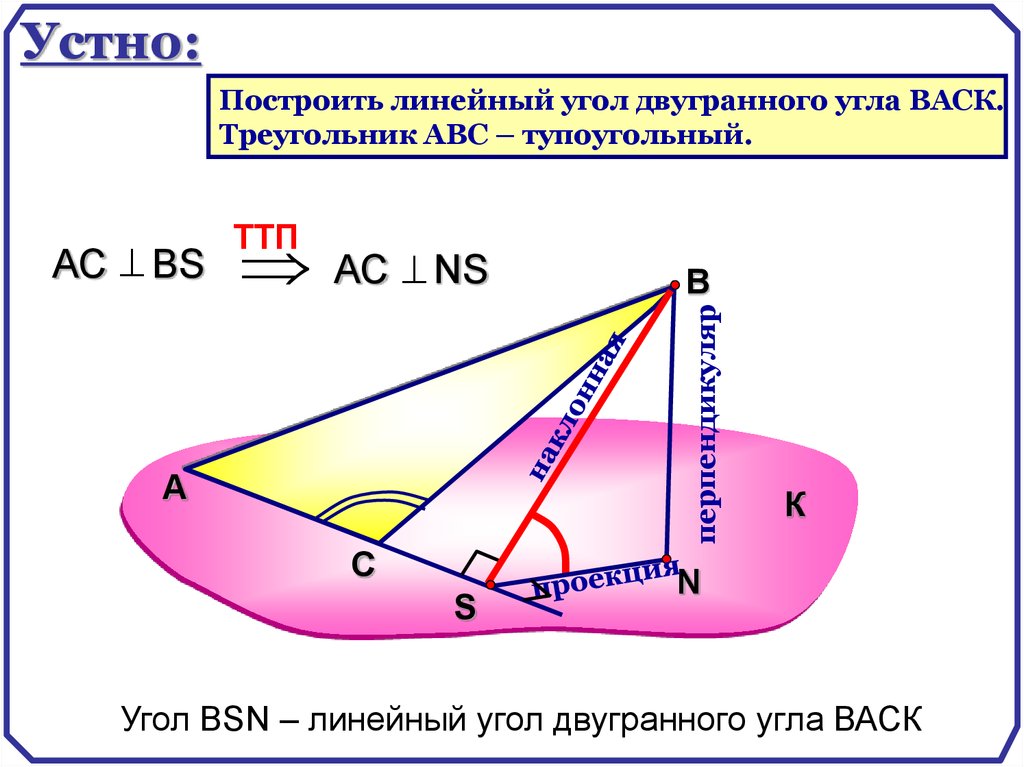
68.

Устно:
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
АС NS
В
перпендикуляр
АС ВS
TTП
А
С
S
К
N
Угол ВSN – линейный угол двугранного угла ВАСК

69.

70.

Устно:
Дан куб. Найдите следующие двугранные углы:
АВВ1С; б) АDD1B; в) А1ВВ1К,
где К середина ребра А1Д1
D1
С1
K
А1
В1
D
А
С
В

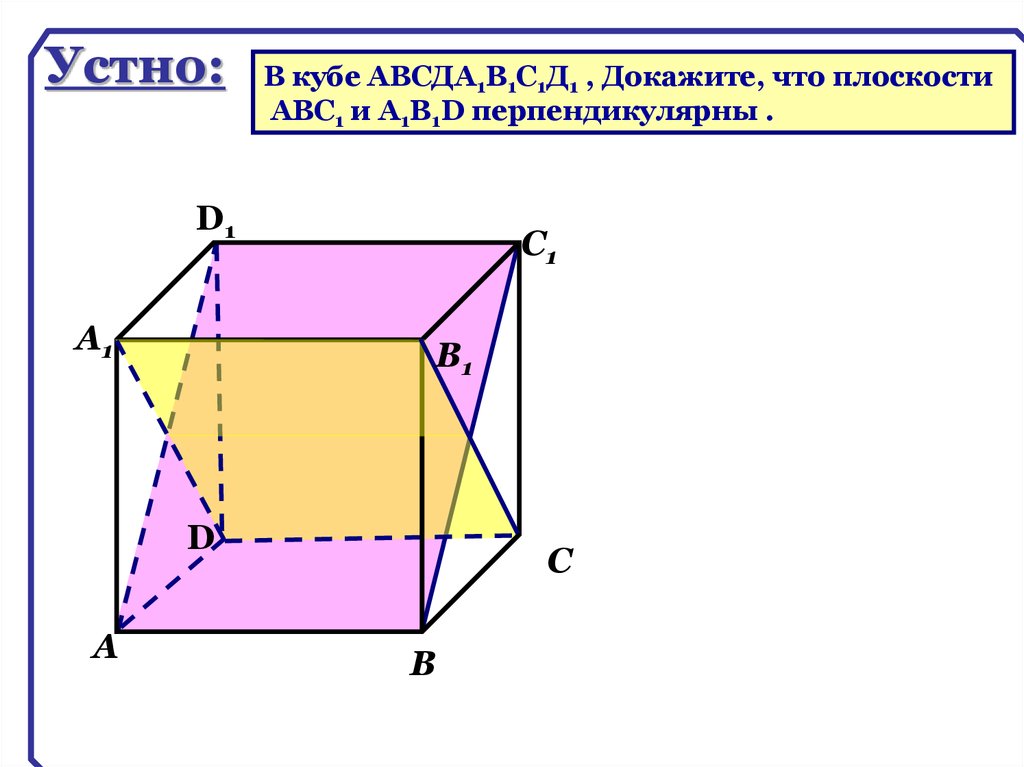
71.

Устно:
В кубе ABCДA1B1C1Д1 , Докажите, что плоскости
АВС1 и А1В1D перпендикулярны .
D1
А1
С1
В1
D
А
С
В

72.

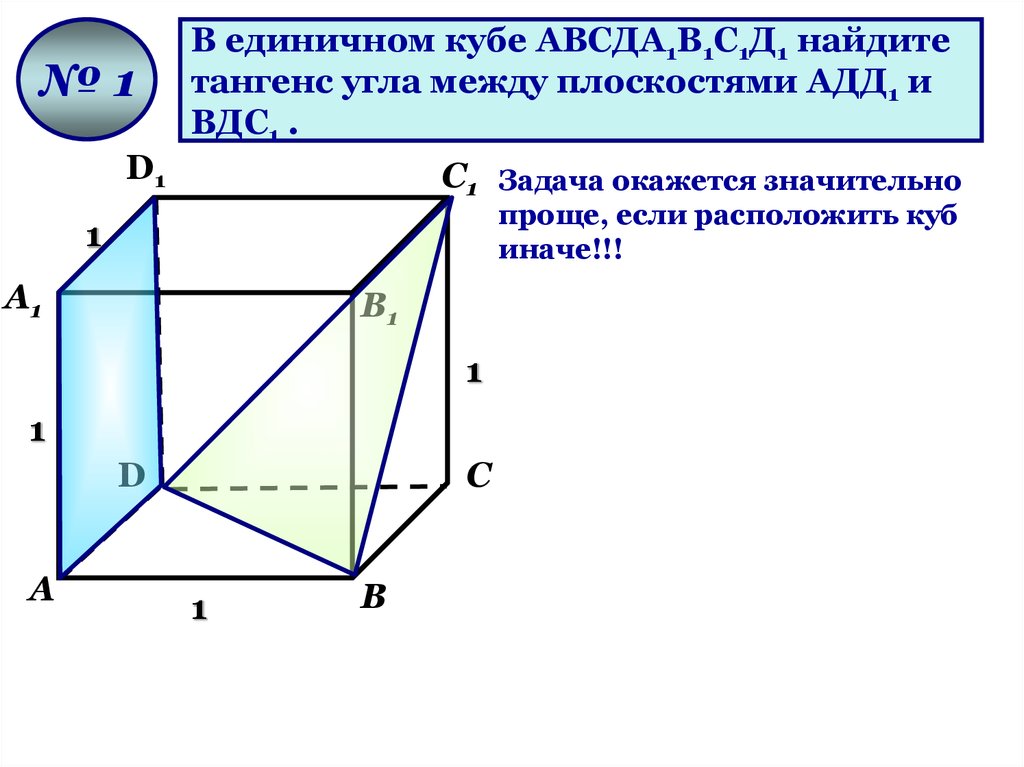
№1
В единичном кубе АВСДА1В1С1Д1 найдите
тангенс угла между плоскостями АДД1 и
ВДС1 .
D1
С1 Задача окажется значительно
проще, если расположить куб
иначе!!!
1
А1
В1
1
1
D
А
С
1
В

73.

№1
В единичном кубе АВСДА1В1С1Д1 найдите
тангенс угла между плоскостями АДД1 и
ВДС1 .
1) Плоскость AДД1 параллельна
А1 плоскости ВСС1, искомый угол
равен углом между плоскостями
ВСС1 и ВДС1 .
ВСС1 ВДС1 ВС
ОС ВС
ДОС
линейный угол
ОД ВС
А
D
1
D1
В
В1
2
2
С
1
О
1
С1
Ответ: 2

74.

№2
1
В единичном кубе АВСДА1В1С1Д1 точки Е, F –
середины ребер соответственно А1В1 и А1Д1.
Найдите тангенс угла между плоскостями
АЕF и ВСС1 .
D1
С1 1) Плоскость AДД1 параллельна
плоскости ВСС1, искомый угол
равен углом между плоскостями
АДД1 и АЕF .
АДД1 АЕF AF
ЕМ AF
АМЕ
линейный угол
АМ AF
F
Е
А1
М
В1
1
D
А
С
Е
Подсказка:
1
2
1
В
А
М
1
5
Ответ: 5
2

75.

В прямоугольном параллелепипеде АВСДА1В1С1Д1,
у которого АВ = 6, ВС = 6, СС1 = 4, найдите тангенс
угла между плоскостями АСД1 и А1В1С1.
№3
D1
6
С1 1) Плоскость AВС параллельна
плоскости А1В1С1, искомый
угол равен углом между
плоскостями АСД1 и А1В1С1 .
6
А1
В1
АВС АД1С АС
4
Д 1О АС
ДО АС
4
D
С
3 2
А
ДОД 1
линейный угол
6
О
6
В
Ответ: 8
3

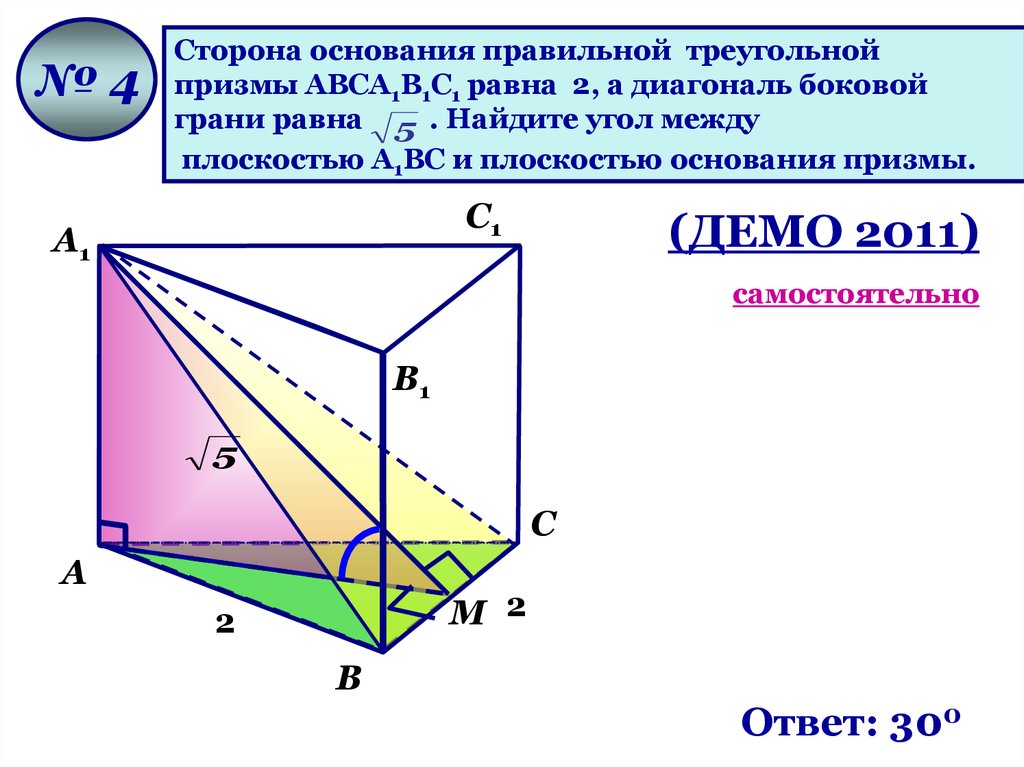
76.

№4
Сторона основания правильной треугольной
призмы ABCA1B1C1 равна 2, а диагональ боковой
грани равна 5 . Найдите угол между
плоскостью A1BC и плоскостью основания призмы.
С1
А1
(ДЕМО 2011)
самостоятельно
В1
5
С
А
М 2
2
В
Ответ: 300

77.

№5
А1
В правильной треугольной призме
АВСА1В1С1 , все ребра которой равны 1,
найдите косинус угла между плоскостями
АСВ1 и ВА1С1.
С1
АСВ1 АВ1С ДЕ
1
3
1
В1М ДЕ
К
КМВ1
2
линейный угол
В1 МК ДЕ
7
4
7
4
1
М
Д
Е
С
А
1
В
Ответ: 17 1

78.

№6
В правильной четырехугольной пирамиде
SАВСД, все ребра которой равны 1. Найдите
косинус двугранного угла, образованного
гранями SВС и SCD.
S
Самостоятельно:
1
К
1
С
D
О
А
1
1
В
Ответ: –1
3

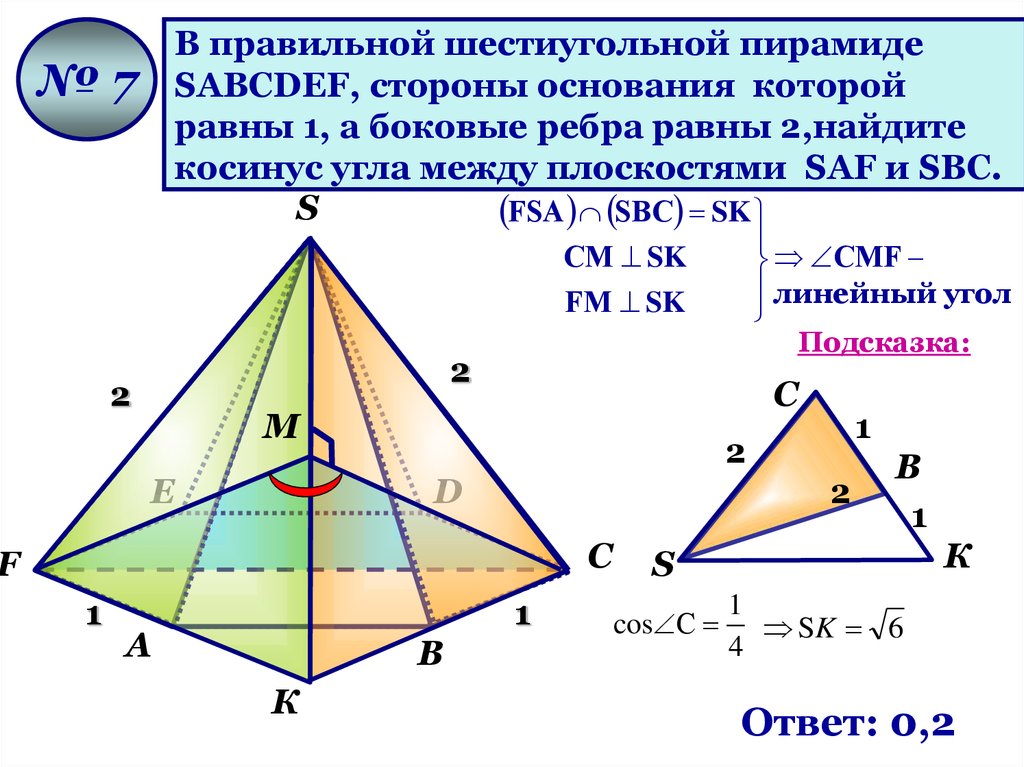
79.

В правильной шестиугольной пирамиде
SАВСDЕF, стороны основания которой
равны 1, а боковые ребра равны 2,найдите
косинус угла между плоскостями SАF и SВС.
S
FSА SВС SK
№7
CМF
линейный угол
Подсказка:
CМ SK
FМ SK
2
2
С
М
Е
2
D
2
С
F
1
1
А
В
К
1
В
1
К
S
1
cos С SK 6
4
Ответ: 0,2

80.

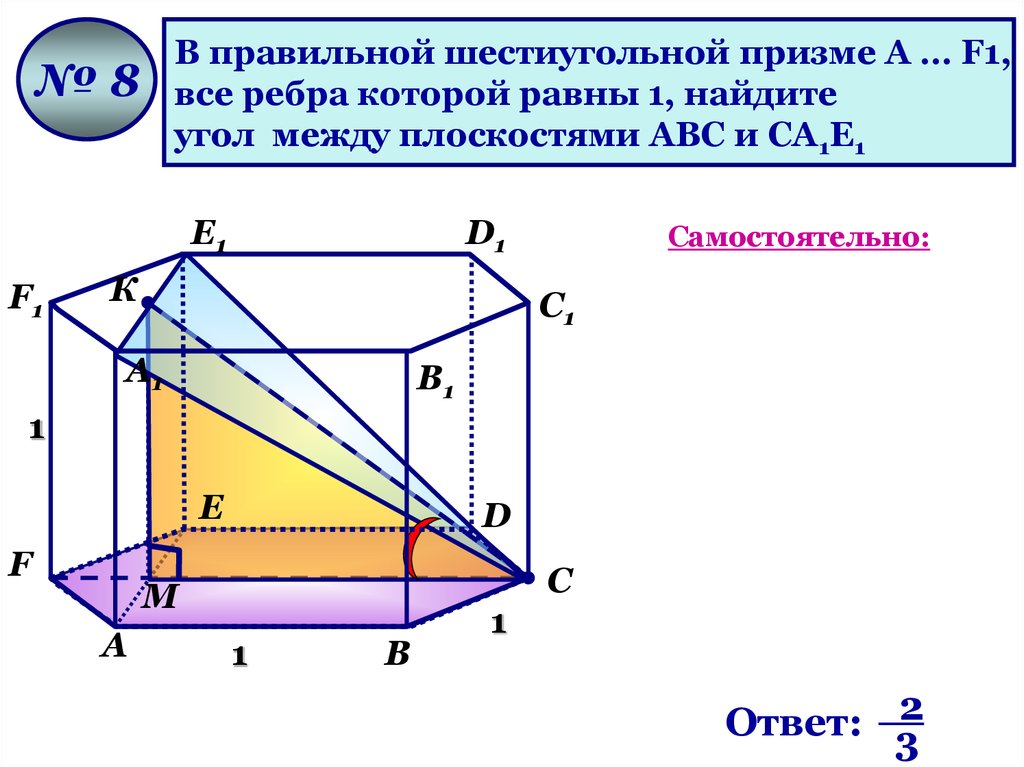
В правильной шестиугольной призме A … F1,
все ребра которой равны 1, найдите
угол между плоскостями AВС и CА1Е1
№8
Е1
F1
D1
К
Самостоятельно:
С1
А1
В1
1
Е
F
D
С
М
А
1
В
1
2
Ответ: 3

81.

Литература
1. В.А. Смирнов ЕГЭ 2011. Математика.
Задача С2. Геометрия. Стереометрия. /
Под. редакцией А.Л. Семенова и И.В.
Ященко. – М.: МЦНМО, 2011.
2. http://le-savchen.ucoz.ru/

English Русский Rules