Similar presentations:
Теория вероятностей
1. Теория вероятностей
Случайные величиныhttp://prezentacija.biz/
2. Схема Бернулли
• Рассмотрим последовательность n независимыходнородных испытаний (экспериментов).
– Испытания считаем независимыми, если результат
испытания не зависит от номера испытания и от того, что
произошло до этого испытания.
– Однородными испытаниями считаем такие, которые
проводятся в одинаковых условиях.
Пусть в каждом испытании событие А может
произойти с вероятностью р
P( A) 1 p q
3. Формула Бернулли
• Вероятность того, что при n испытаниях• событие А наступит к-раз:
Pn (k ) Cnk p k q n k
где Cnk число сочетаний
n!
С
k!(n k )!
k
n
4. Схема Бернулли
• Пример.• Вероятность того, что образец бетона при испытании выдержит
нормативную нагрузку, равна 0,9.
• Найти вероятность того, что из 7 образцов 5 выдержат испытания.
• Решение.
• По формуле Бернулли
7!
5
2
P C p q
0,9 0,1 0,124
5! 2!
5
7
5
7
5
2
5. Схема Бернулли
• Асимптотические формулы.• 1. Формула Пуассона.
• Пусть число испытаний n - велико ( n→∞ )
• Вероятность р события А – мала ( р→0 )
• Причем
np a
• Тогда при любом фиксированном к
k
a a
Pn (k )
e
k!
Закон редких событий
( n 100 , a np 10 )
6. Схема Бернулли
• Пример 1 .Известно, что при транспортировке 2,5% декоративной плитки
повреждается. Определить вероятность того, что в партии из 200 плиток
оказалось поврежденными:
а) ровно 4 плитки; б) не более 6 плиток.
• Решение.
Вероятность того, что плитка окажется поврежденной,
р=0.025 – мала, число испытаний n=200 –велико, причем np=5<10.
По формуле Пуассона:
а)
5 4 5
P200 (4) e 0,18
4!
i
5
P200 (i 6) e 5 0,76
i 0 i !
6
б)
7. Схема Бернулли
• 2. Локальная теорема Муавра-Лапласа.• Пусть число испытаний n – велико (n→∞)
• Вероятность р события А – не очень мала ( 0<<р<<1 )
(р не близко к 0 и к 1)
• Тогда при любом фиксированном к
Pn (k )
1
( x) ,
npq
где ( x)
e
x2
k np
, x
2
npq
2
8. Схема Бернулли
• 3. Интегральная теорема Муавра-Лапласа.Пусть число испытаний n – велико (n→∞)
Вероятность р события А – не очень мала ( 0<<р<<1 )
(р не близко к 0 и к 1)
Тогда вероятность того, что событие А наступит
не менее к-раз и не более m-раз,
приближенно равна P ( k i m) ( x ) ( x )
n
1
где ( x)
2
x
e
2
t 2
0
k np
m np
x1
, x2
npq
npq
2
dt
1
функцияЛап ласа
9. Схема Бернулли
• Пример 2 .• Завод изготавливает 80% высоконапорных железобетонных
труб первого сорта.
• Определить вероятность того, что из 100 труб 75 будет первого
сорта.
• Решение.
• n =100 – велико, р=0,8 –не близко к 0 и к 1.
• По локальной теореме Муавра –Лапласа:
P100 (75)
1
1
75 80
( x)
(
)
npq
100 0,8 0,2
100 0,8 0,2
0,25 ( 1,25) 0,046
10. Схема Бернулли
• Пример 3 .• Вероятность поражения цели при одном выстреле равна 0,8.
• Производится 100 выстрелов.
• Норматив считается выполненным, если цель будет поражена не
менее 75 раз.
• Определить вероятность выполнения норматива.
• Решение.
• По интегральной теореме Муавра-Лапласа:
100 100 0,8
75 100 0,8
P100 (75 i 100) (
) (
)
100 0,8 0,2
100 0,8 0,2
(5) ( 1,25) 0,5 0,3943 0,89
11. Оценка отклонения относительной частоты от постоянной вероятности
• Задача.Производится n независимых однородных испытаний.
В каждом испытании событие А может наступить
с вероятностью р, где 0 << р << 1.
k
Найти вероятность того, что относительная частота
n
отклонится от вероятности р (по абсолютной величине)
не более чем на
ε>0 :
k
P( p ) ?
n
12. Оценка отклонения относительной частоты от постоянной вероятности
kp np n k np n
n
Решение.
По интегральной теореме Муавра-Лапласа:
k
P ( p ) P(np n k np n )
n
( x2 ) ( x1 ) ,
где
(np n ) np
n
(np n ) np
x1
, x2
pq
npq
npq
n
pq
13. Оценка отклонения относительной частоты от постоянной вероятности
Тогда
k
n
n
n
P ( p ) (
) (
) 2 (
)
n
pq
pq
pq
Анализ :
0 при n P( p ) 1
P( p ) 0
k
n
14. Случайная величина
• Определение.• Случайной величиной называется числовая величина
(числовая функция), значение которой может меняться в
зависимости от результата стохастического эксперимента.
– Обозначения:
X , Y , Z ... или , , ...
Пример 1.
– 1. Число вызовов, поступивших от абонентов на
телефонную станцию в течение определенного
промежутка времени, является случайным и принимает
те или иные значения в зависимости от случайных
обстоятельств.
15. Случайная величина
• Пример 2.• Рассмотрим схему Бернулли:
• последовательность n независимых однородных испытаний,
• событие А – случайное событие, которое может наступить
при каждом испытании.
{ } пространство элементарных событий,
где ( 1 , 2 ,..., n )
• i 1 , если при i-ом испытании событие А наступило, и
• i 0 , если оно не наступило.
• Случайная величина
1
2
n
• - число наступлений события А в схеме Бернулли.
X ...
16.
Случайнаявеличина
дискретная
непрерывная
17. Случайная величина
• Дискретная случайная величина – такая случайнаявеличина, которая может принимать конечное или счетное
множество значений.
• Значения непрерывной случайной величины –
принадлежат интервалу (конечному или бесконечному).
18. Случайная величина
• Пример 3. Рассмотрим схему Бернулли:• последовательность n независимых однородных испытаний,
• А – случайное событие, которое может наступить при каждом
испытании.
• Пусть Х – число наступлений события А.
Х={ 0,1,2,…,п } – дискретная случайная величина.
• Пример 4.
• Проводятся независимые однородные испытания до первого
появления события А.
• Пусть ξ – функция, равная числу испытаний, проведенных до
первого появления события А.
ξ={0,1,2,3,…} –дискретная случайная величина.
Обзор
19. Случайная величина
• Пример 5.• Случайным образом бросают точку на отрезок [ а,в ].
• Х – координата точки попадания.
• Х є [ а,в] – непрерывная случайная величина.
• Пример 6.
• Время работы прибора без поломки μ – непрерывная
случайная величина.
μ є ( 0, ∞ )
20. Способы задания случайной величины
• Функция распределения и ее свойства.• Определение.
F (x) , равная вероятности того, что случайная
Функция
величина
примет значение меньше х, называется функцией
распределения:
F ( x) P( x)
• Свойства.
1. Область определения F(x): х є (-∞, ∞).
2. Область значений : 0 ≤ F(x) ≤ 1.
3. Функция F(x) – неубывающая: x1 x2 F ( x1 ) F ( x2 )
4.
5. Вероятность попадания в интервал (а,в):
lim F ( x) 0 , lim F ( x) 1
x
x
P (a b) F (b) F (a)
21. Закон распределения дискретной случайной величины
• Определение.• Закон распределения дискретной случайной величины – это
соответствие между возможными значениями и
вероятностями, с которыми эти значения принимает
случайная величина.
• Способы задания:
• Таблично
Графически
ξ
Р
x1
p1
…
…
0,7
xn
0,6
0,5
0,4
pn
0,3
k
a a
Аналитически P( k )
e
k!
0,2
0,1
0
x1
x2
…
xn
многоугольник распределения
22. Закон распределения дискретной случайной величины
• Примеры.• 1. Биномиальный закон ( в схеме Бернулли):
P( k ) Cnk p k q n k
• 2. Равномерное распределение ( в классической схеме):
P ( k )
1
n
• 3. Распределение Пуассона:
a k a
P( k ) e
k!
23. Дискретная случайная величина
• Основное свойство• закона распределения:
p
i
1
(i )
• Функция распределения –
кусочно- непрерывная
функция.
• График функции
распределения –
ступенчатая фигура.
F ( x) pi
xi x
F (x)
1
p1
x1
x2
xn
х
24. Непрерывная случайная величина
• Определение.• Случайная величина ξ называется непрерывной, если
ее функция распределения F(x)- непрерывная при
всех х и имеет почти всюду производную F'(x)=f(x).
• В этом случае функция f(x) называется плотностью
распределения вероятности.
• Замечания. В некоторых учебниках такие случайные
величины называют абсолютно непрерывными.
• Если F(x)- непрерывная и не дифференцируемая
функция, то в этом случае случайную величину
называют сингулярной.
25. Свойства плотности распределения
f ( x) 0• 1.
• 2.
f ( x)dx 1
b
• 3.
P(a b) f ( x)dx
a
x
• 4.
F ( x)
f (t )dt
26. Непрерывная случайная величина
• Пример.Случайным образом бросают точку на отрезок [ 0,1 ].
ξ– координата точки попадания.
Найти функцию распределения F(x) и плотность f(x).
Решение.
Из определения:
0 , если x
F ( x) P( x)
f ( x) F ( x)
Обзор
0
F ( x) х , если х (0,1]
1 , если х 1
0 , если x 0
f ( x) 1 , если х (0,1]
0 , если х 1
27. Непрерывная случайная величина
F (x)1
0
1
x
1
x
f (x)
1
0
28. Числовые характеристики случайных величин
• Математическое ожидание.• Определение.
Математическим ожиданием
дискретной случайной величины ξ
называется число, равное
M xi pi
(i )
где
xi значения случайной величины ,
pi их вероятности.
29. Числовые характеристики случайных величин
Математическим ожиданием
непрерывной случайной величины ξ
называется число, равное
M
x f ( x)dx
где
f ( x) плотность распределения.
30. Числовые характеристики случайных величин
• Свойства математического ожидания.• 1.
• 2.
• 3.
M (C ) C , где С постоянная.
M (C ) C M ( )
M ( ) M ( ) M ( ),
где и случайные величины.
• 4. M ( ) M ( ) M ( ) ,
если и независимые случайные величины.
31. Числовые характеристики случайных величин
• Пример 1.Случайным образом бросают точку на отрезок [ 0,1 ].
ξ– координата точки попадания.
Найти математическое ожидание M ( )
Решение.
Из определения: M ( ) x f ( x ) dx
0 , если x 0
f ( x) 1 , если х (0,1]
0 , если х 1
1
2 1
x
M ( ) x dx
2
0
0
1
2
32. Числовые характеристики случайных величин
• Дисперсия случайной величины.Определение.
Дисперсией случайной величины ξ называется
математическое ожидание квадрата отклонения
случайной величины от ее
математического ожидания:
D( ) M ( a) 2 ,
где a M ( )
33. Числовые характеристики случайных величин
• Свойства дисперсии.• 1. D (C ) 0
D(C ) C D( )
3. D( ) D( ) D( ) ,
если и независимые случайные величины.
2
• 2.
• 4. Следствие.
D( ) D( ) D( ) ,
если и независимые случайные величины.
34. Числовые характеристики случайных величин
D( ) M ( ) a2
2
Доказательство.
D( ) M ( a) 2 M ( 2 2a a 2 )
M ( 2 ) 2a M ( ) M (a 2 )
M ( 2 ) a 2 ,
так как
a M ( )
35. Числовые характеристики случайных величин
• Среднеквадратическое отклонениеслучайной величины.
• Определение.
Среднеквадратическим отклонением
случайной величины ξ называется число
( ) D( )
• Свойства.
• 1. ( )
• 2. (C )
0 , ( ) 0 C
C ( )
36. Числовые характеристики случайных величин
• Пример 2.Случайным образом бросают точку на отрезок [ 0,1 ].
ξ– координата точки попадания.
Найти дисперсию и
среднеквадратическое отклонение.
Решение.
2
2
D
(
)
M
(
)
a
Из формулы:
1
0 , если x 0
f ( x) 1 , если х (0,1]
0 , если х 1
1
a M ( )
2
3 1
x
M ( ) x dx
3
0
2
2
0
1 1 1
D( )
3 4 12
1
1
( )
12 2 3
1
3
37. Обзор стандартных распределений
Дискретные случайные величиныБиномиальное распределение
Распределение Пуассона
Геометрическое распределение
38. Обзор стандартных распределений
Непрерывные случайные величиныРавномерное распределение
Показательное распределение
Нормальное распределение
39. Биномиальное распределение
• ξ=(число «успехов» при n испытаниях в схеме Бернулли).• Закон распределения:
P( k ) C p q
k
n
k
n k
p вероятность "успеха" ,
q 1 p ; k 0 , 1 ,..., n.
n , p параметры распределения .
M ( ) a np
Пример
D( ) 2 npq
npq
40. Распределение Пуассона
• ξ=(0,1,2,…,n,…)• Закон распределения:
k
a a
P( k ) e
k!
a параметр распределения .
M ( ) a
D ( ) a
a
41. Геометрическое распределение
• ξ=(0,1,2,…,n,…)• Закон распределения:
P( k ) p q
k
p параметр распределения
вероятность "успеха"
q
М ( )
p
Пример
q
D( ) 2
p
q
p
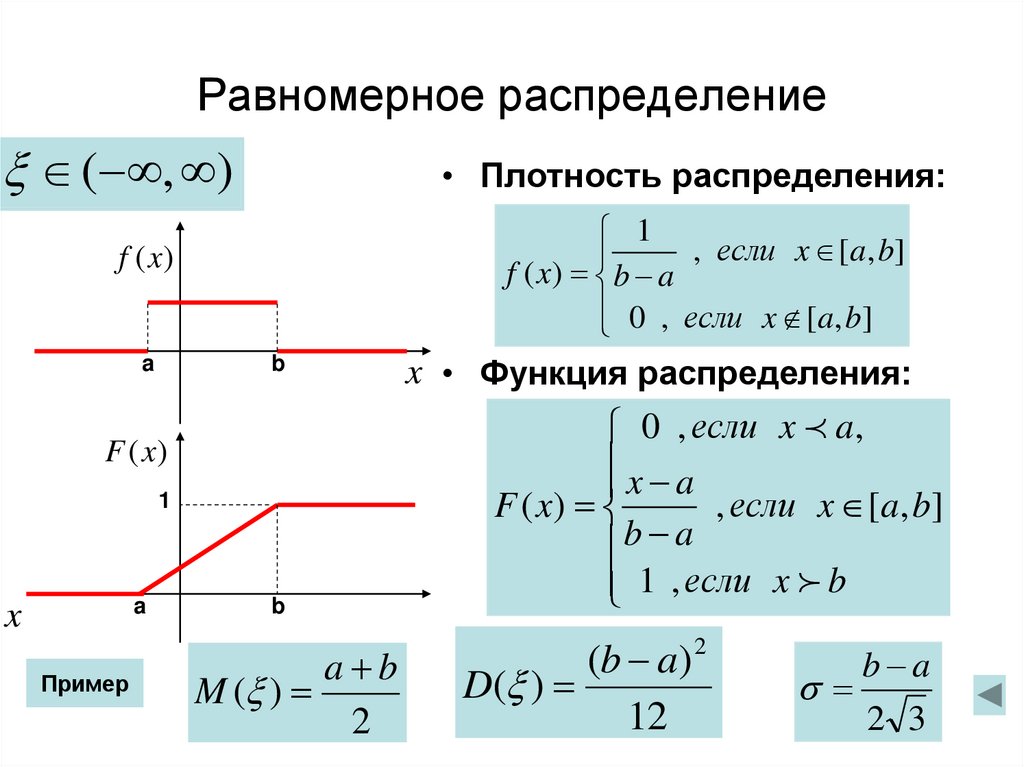
42. Равномерное распределение
( , )• Плотность распределения:
1
, если x [a, b]
f ( x) b a
0 , если x [a, b]
f (x)
a
b
F (x)
1
a
x
Пример
b
a b
M ( )
2
x • Функция распределения:
0 , если x a,
x a
F ( x)
, если x [a, b]
b a
1 , если x b
(b a)
D( )
12
2
b a
2 3
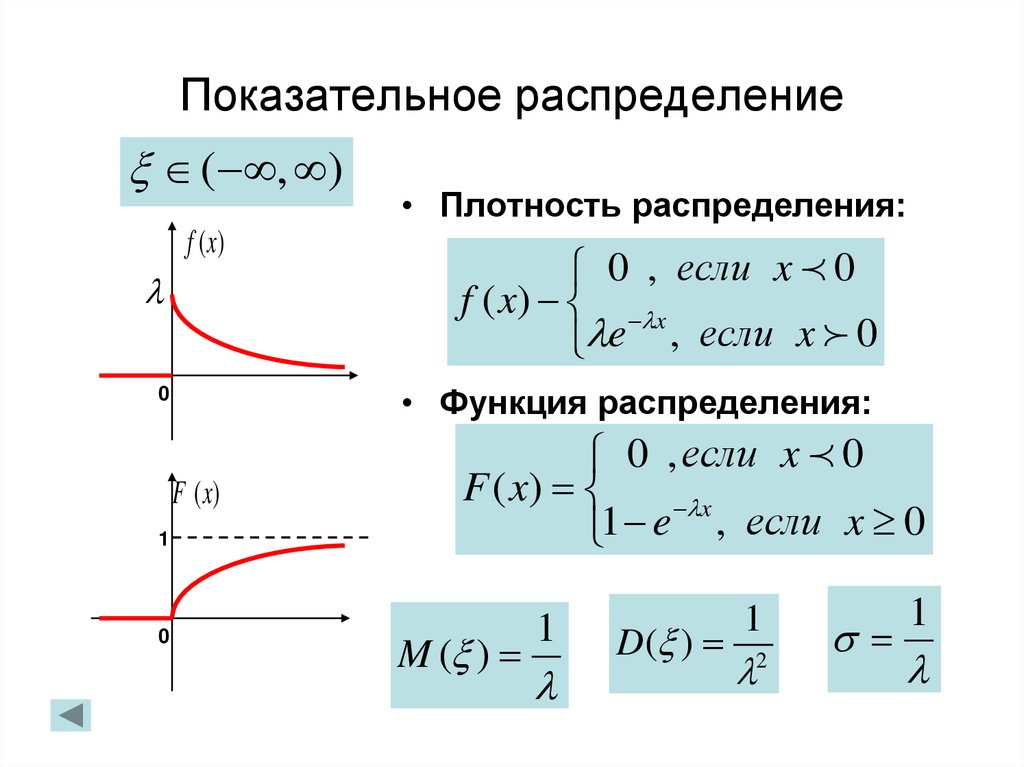
43. Показательное распределение
( , )f (x)
F (x)
0
0 , если x 0
f ( x) x
e , если x 0
• Функция распределения:
0
1
• Плотность распределения:
0 , если x 0
F ( x)
x
1 e , если x 0
M ( )
1
D ( )
1
2
1
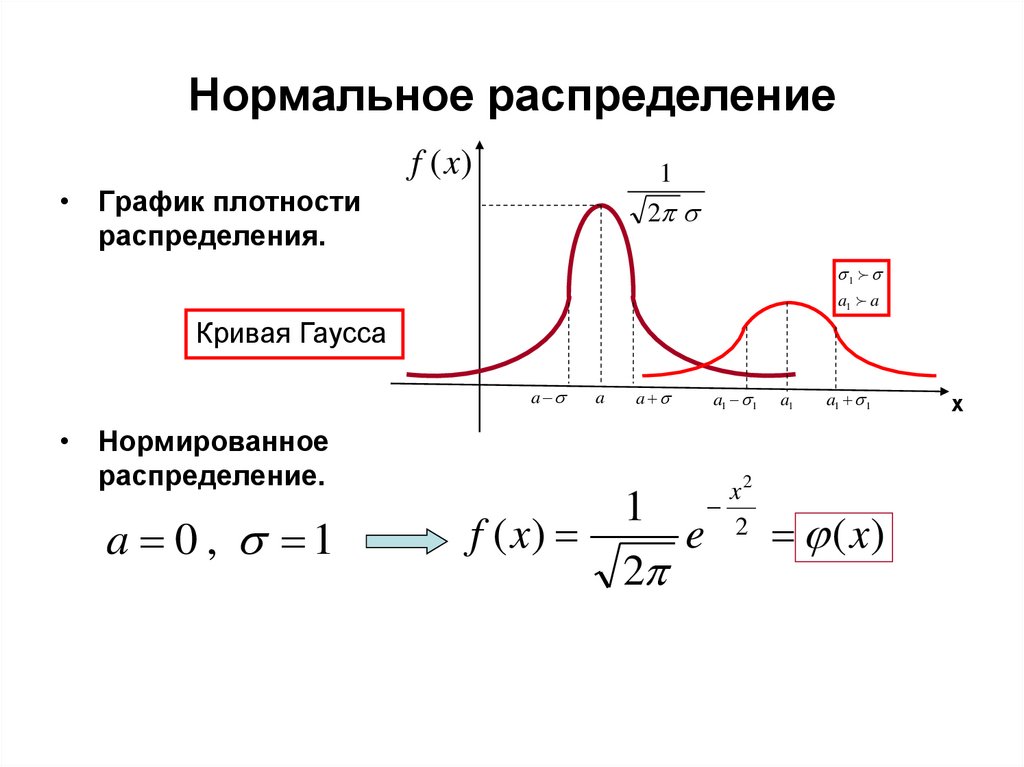
44. Нормальное распределение
• Определение.Непрерывная случайная величина ξ
имеет нормальное распределение
с параметрами a и σ,
если плотность распределения
1
f ( x)
e
2
( x a )2
2 2
• Вероятностный смысл параметров:
a M ( ) , D( )
~ N ( a, )
45. Нормальное распределение
f (x)1
2
• График плотности
распределения.
1
a1 a
Кривая Гаусса
a
• Нормированное
распределение.
a 0 , 1
a
a
1
f ( x)
e
2
a1 1
x2
2
a1
a1 1
( x)
х
46. Нормальное распределение
• Функция распределения.x
1
F ( x) f (t )dt
2
1
2
a
e
x
e
x
dt
1
2
dt
(t a )2
2 2
(t a )2
2 2
1
e
2 a
(t a )2
2 2
dt
x a
функция Лапласа
1
x a
F ( x)
2
47. Нормальное распределение
• Вероятность попадания в интервал.P ( x1 x2 ) F ( x2 ) F ( x1 )
x2 a
x1 a
• Следствие:
• (вероятность отклонения ξ от а не более чем на ε)
P( a ) P(a a )
a a
a a
P( a ) 2
48. Нормальное распределение
• Правило «3σ».3
P( a 3 ) 2
2 (3) 0,9973
Практически достоверно, что
N (a, ) [a 3 , a 3 ]
49. Нормальное распределение
• Пример.• Отклонение длины изготавливаемой детали от
стандарта
• - случайная величина, распределенная по
нормальному закону.
• Если стандартная длина – 40 см, а
среднеквадратическое отклонение – 0,4 см, то
какое отклонение длины изделия от стандарта
можно ожидать с вероятностью 0,8 ?
• Решение.
P( a ) 2
a 40 , 0,4
1,285
0,8 0,4
0,514
39,486 40,514
50. Функции случайного аргумента
• Определение.Если любому значению случайной величины Х
соответствует одно возможное значение
случайной величины Y, то говорят что
Y – функция случайного аргумента Х:
Y ( X )
• Пример.
• Х – случайная величина.
• Y=X² или Y = (Х-а)² -функции от Х.
51. Функции случайного аргумента
X дискретная случайная величинаpi P( X xi )
Y ( X ) дискретная случайная величина
монотонная функция
yi ( xi )
P (Y yi ) P ( X xi ) pi
не монотонная функция
P(Y yi ) ?
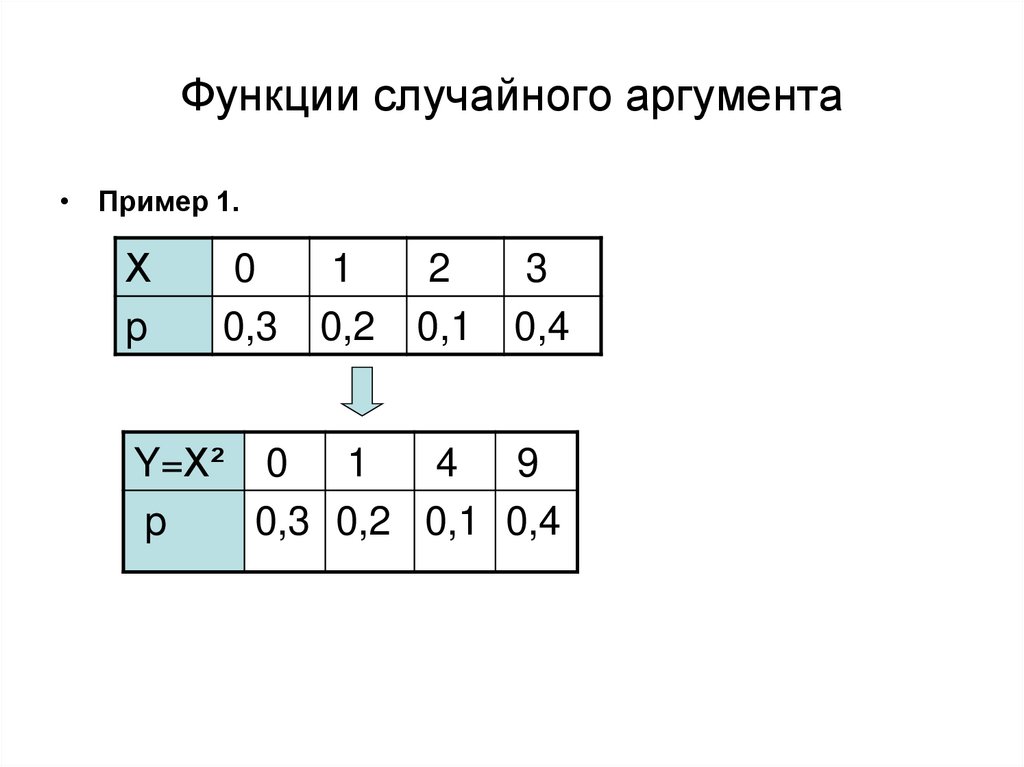
52. Функции случайного аргумента
• Пример 1.Х
p
0
0,3
1
0,2
2
0,1
3
0,4
Y=Х² 0 1
4 9
p
0,3 0,2 0,1 0,4
53. Функции случайного аргумента
• Пример 2.X
p
-2 -1 0 1 2 3
0,1 0,2 0,3 0,2 0,1 0,1
Y=Х²
p
0
0,3
1
0,4
4
0,2
9
0,1
54. Системы случайных величин
• В случае, когда результат стохастического экспериментаопределяется несколькими случайными величинами, то
говорят, что имеется система случайных величин:
1 , 2 ,..., n - (случайный вектор), i - компоненты
• Примеры. 1. Заготовка имеет 3 размера –
» длину, ширину и высоту – случайные величины:
x , y , z
» 2. при моделировании бюджета одной семьи
» затраты – случайный вектор: на питание, на одежду,
» обувь, на транспорт, духовные потребности.
55. Системы случайных величин
X , Y• Двумерные случайные величины
• Дискретные - закон распределения
X Y
y1
y2
….
ym
x1
p11
p12
….
p1m
x2
p21
p22
….
p2m
….
….
….
….
….
xn
pn1
pn2
….
pnm
pij P( X xi , Y y j )
p
i, j
ij
1
56. Системы случайных величин
• Непрерывные - функция распределенияF ( x, y ) P ( X x, Y y )
y
» - вероятность попадания в бесконечный угол
Свойства
(x,y)
F ( x, y )
1.
0 F ( x, y ) 1
2.
F ( x, y ) не убывает по
3.
lim F ( x, y ) 1,
x
каждому аргументу
x , y
lim F ( x, y ) 0
x , y
57. Системы случайных величин
• Плотность распределения вероятностей случайного вектора.• Определение.
• Плотностью распределения случайного вектора
F ( x, y )
f ( x, y )
x y
2
• называют
• Свойства плотности
• 1.
f ( x, y ) 0
• 2.
f ( x, y)dxdy 1
x y
3.
F ( x, y )
f (u, v)dudv
4.
P( x1 X x2 ; y1 Y y2 )
x2 y 2
f (u, v)dudv
x1 y1
58. Системы случайных величин
• Зависимость случайных величин.• Случайный вектор X , Y ;
f ( x, y ) -
плотность,
F ( x, y ) - функция распределения.
• Определение.
• Случайные величины
Х
и
Y (компоненты случайного вектора)
• называются независимыми, если
P( X x, Y y ) P( X x) P(Y y
• Следствия. 1.
2.
F ( x, y) FX ( x) FY ( y)
f ( x, y) f X ( x) fY ( y)
для независимых
случайных величин
59. Системы случайных величин
• Ковариация. Коэффициент корреляции.• Определение 1.
X и Y называют число
cov( X , Y ) M [( X M ( X )) (Y M (Y ))]
• Ковариацией случайных величин
• Определение 2.
• Коэффициентом корреляции случайных величин
называют число
cov( X , Y )
( X ,Y )
( X ) (Y )
X
и
Y
60. Системы случайных величин
• Свойства.• 1. Если
X
и
Y – независимые
cov( X , Y ) 0
2. ( X , Y ) 1
3. Если
X и Y–
Y A X B
случайные величины, то
( X ,Y ) 0
[обратное неверно]
линейно зависимые, то есть
, то
1, если A 0,
( X ,Y )
1, если A 0
61. Моменты случайной величины
• Определение 1.• Начальным моментом случайной
• величины Х порядка n
d M (X )
• называют математическое ожидание
n
:
n
X
n
• Определение 2.
• Центральным моментом случайной
• величины Х порядка n
• называют математическое ожидание
( X : a)
n
n M (( X a) ) , где a M ( X )
n
62. Моменты случайной величины
• Определение 3.• Абсолютным центральным моментом
• случайной величины Х порядка n
n
• называют математическое ожидание X a :
M( X a )
n
– Частные случаи:
• 1) М(Х)=а – начальный момент 1-го порядка ;
• 2) М((Х-а))=0 – центральный момент 1-го порядка;
• 3) М((Х-а)²)=D(X ) – центральный момент 2-го порядка.
63.
Предельныетеоремы
Закон больших чисел
Центральная
предельная теорема
64. Неравенство Чебышева
M ( X ) a , D( X ) 2• Пусть Х – случайная величина;
0 : P( X a ) 2
2
• Следствие: Чем меньше дисперсия случайной величины Х, тем
меньше вероятность отклонения Х от а на большую величину.
• Правило «3σ» (для любой случайной величины):
2
0 : P( X a ) 1 2
1
3 , P( X a 3 ) 1 0,8(8)
9
( X ~ N (a, ) P 0,9973)
65. Закон больших чисел
• Определение.• Последовательность случайных величин
• X 1 , X 2 , ... , X n , ... сходится по вероятности
• к случайной величине Х, если
0 : lim P( X n X ) 0
n
(или 0 : lim P( X n X ) 1)
n
– Обозначение:
p
Xn
X
66. Закон больших чисел
• Теорема Чебышева.• Пусть
X 1 , X 2 , ... , X n , ... - попарно независимые
случайные величины; D( X ) C n
n
X 1 X 2 ... X n
a1 a2 .. an
p
n
n
• Среднее арифметическое независимых случайных величин
• при n – больших
- неслучайная величина.
67. Закон больших чисел
• Теорема Хинчина (1929 г.).Пусть
Тогда
1 , 2 ,..., n ,...- независимые случайные величины, M ( i ) a
p
1 n
i a
n i 1
При достаточно большом числе независимых опытов
• среднее арифметическое наблюденных значений
случайной величины сходится по вероятности к ее
математическому ожиданию.
– Практический смысл: при измерении физической величины в
качестве точного значения берут среднее арифметическое
нескольких измерений.
68. Центральная предельная теорема
• Теорема.• Пусть X 1 , X 2 , ... , X n , ... - независимые случайные
величины, имеющие один и тот же закон распределения с
математическим ожиданием а и дисперсией σ² .
• Пусть Yn
величины.
• Тогда Yn
• то есть
1
n
(X
n
i 1
i
a)
- нормированные случайные
n
Y ~ N (0,1)
P(Yn [a, b]) n
1
2
b
e
a
x2
2
dx
69. Центральная предельная теорема
• Теорема Ляпунова (1901 г.).• Пусть
X 1 , X 2 , ... , X n , ... - независимые случайные
величины, имеющие конечный третий абсолютный
центральный момент
cn M ( X n a n ) .
3
Yn X 1 X 2 ... X n
An a1 a2 ... an и Bn 12 22 ... n2
• Пусть
Cn 3 c1 c2 ... cn
Cn
Тогда , если lim
0
n B
n
, то
Yn An
n
Y ~ N (0,1)
Bn
70. Центральная предельная теорема
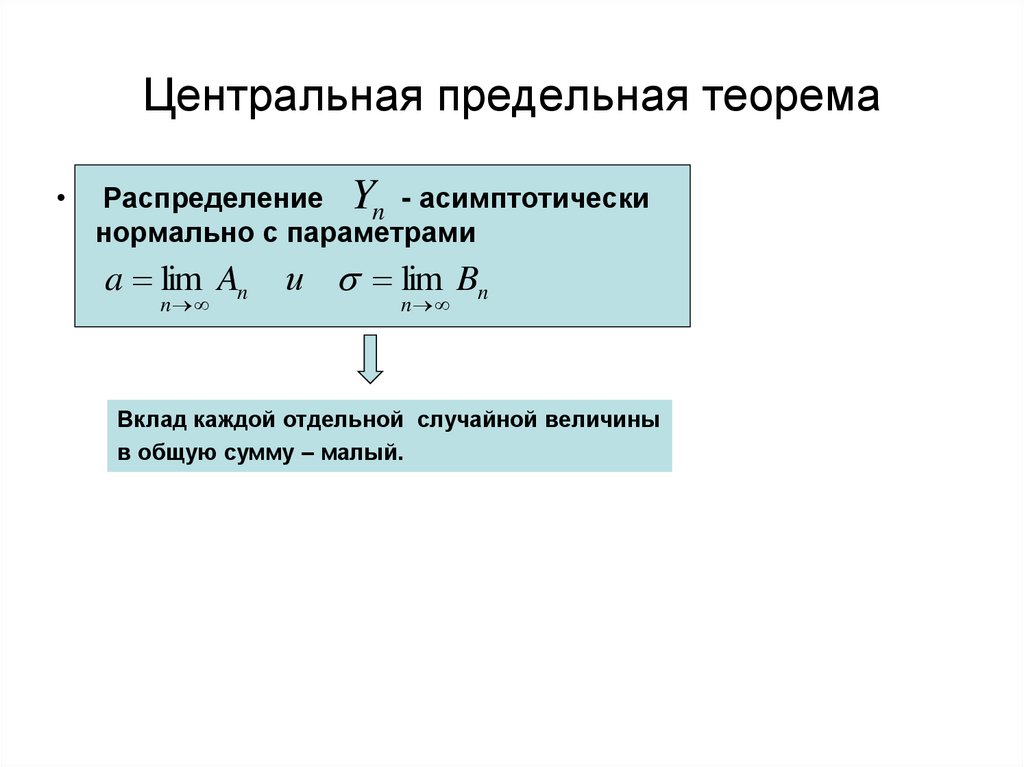
Распределение Yn - асимптотически
нормально с параметрами
a lim An
n
и lim Bn
n
Вклад каждой отдельной случайной величины
в общую сумму – малый.
71. Центральная предельная теорема
• Следствие: нормальный закон занимает особое место втеории ошибок измерений.
Ошибку измерения можно рассматривать как сумму большого
числа независимых слагаемых, каждое из которых дает малый
вклад в общую сумму.
Распределение ошибки измерений близко к
нормальному закону.
Замечание (Липман).
– Каждый уверен в справедливости закона ошибок:
• Экспериментаторы – потому что они думают,
что это математическая теорема,
• Математики – потому что они думают, что это
экспериментальный факт.
72. Центральная предельная теорема
• Пример.В геодезии причинами возникновения ошибок являются
–
–
–
влияние внешних условий
неточности изготовления и юстировки приборов
неточности выполнения измерений наблюдателем
• При измерении горизонтального направления
– многократное преломление лучей
– неравномерное освещение объекта
– неустойчивость сигнала
– вращение прибора вследствие нагревания солнцем («кручение»)
– неустойчивость теодолита
– температурные и другие изменения в приборе
– ошибки юстировки
– ошибки разделения горизонтального круга
– личные ошибки наблюдателя
– и т.д.
Опыт подтверждает - распределение ошибки
измерений близко к нормальному закону.



































































 physics
physics








